基于积分滑模控制的无人机自动着舰系统

郑峰婴, 龚华军, 甄子洋

(1. 南京航空航天大学航天学院, 江苏 南京 210016;

2. 南京航空航天大学自动化学院, 江苏 南京 210016)



基于积分滑模控制的无人机自动着舰系统

郑峰婴1, 龚华军2, 甄子洋2

(1. 南京航空航天大学航天学院, 江苏 南京 210016;

2. 南京航空航天大学自动化学院, 江苏 南京 210016)

摘要：针对无人机着舰这一特殊环境,为克服系统摄动、未建模动态及各种环境干扰因素的不良影响,从工程实现易行性出发,提出一种新的积分滑模着舰飞行控制方法,避免其受传统积分切换函数滑模控制方法的应用限制,并采用自适应模糊系统抵消外界干扰带来的误差,逼近滑模控制器中的切换项,从而有效降低舵面的抖振。搭建自动着舰综合仿真平台,以国外现役某小型舰载无人机为例,仿真结果表明,该自动着舰系统能较好地克服各种因素的影响,实现无人机安全着舰,着舰性能符合要求。

关键词：舰载无人机; 自动着舰; 飞行控制; 积分滑模; 自适应模糊

0引言

舰载无人机因其出色的海战能力备受各海军强国的关注,已成为未来大中型舰艇的重要装备之一[1-2],其关键技术是如何在恶劣的着舰环境下保证无人机安全着舰[3]。由于技术不公开,国内外在这一方面公开报道的研究成果较少。

针对着舰这一特定环境,提高系统的鲁棒性、抗干扰能力是舰载无人机控制系统开发的重点和难点。目前用于完成着舰任务的无人机控制方法普遍采用经典控制方法,例如文献[4-5]在无人机内外控制回路中,均采用PID方法对各通道进行设计,完成控制性能和着舰性能分析。文献[6]采用改进的(linear quadratic regulator, LQR)控制方法设计无人机纵向着舰控制系统,以确定无人机纵向气动参数设计限值。先进控制方法在着舰中的应用也偶有报道,如文献[7]采用动态逆控制方法评估非线性控制技术在自动航母着舰系统中应用的可行性。文献[8]提出一种自适应自动着舰算法,以提高无人机机动能力。

但以上这些研究都没有综合考虑系统摄动、未建模动态及系统的抗干扰能力。

为解决这一问题,同时考虑工程实现的易行性,本文采用变结构滑模控制方法,该方法对系统不确定和外干扰具有很好的鲁棒性,在飞控系统中也有所应用。例如，文献[9]采用反步自适应滑模变结构控制方法设计飞机大机动飞行控制系统,以提高系统鲁棒性；文献[10]针对某型鹞式飞机的飞行控制系统,提出了基于滑模控制方法的鲁棒动态逆控制方法,以提高系统的鲁棒；文献[11]设计基于滑模观测器的控制方法的F-18飞行重构控制系统,以达到理想控制效果。

然而,变结构滑模控制在无人机着舰系统中的研究尚未见有深入报道。设计基于滑模控制的舰载无人机飞控系统时,必须考虑到舰基飞机与陆基飞机的降落环境有很大区别。

一方面,由于航母前进方向与斜角甲板之间有夹角,会存在一个固定的侧偏值,使系统出现稳态误差。普通的滑模变结构控制不能很好地解决该问题,因此,考虑采用积分滑模控制[12]。文献[13]针对单输入不确定伺服系统,设计了一种带有积分切换函数的滑动模面,当系统处于滑模面时,可根据状态反馈阵配置极点,增强系统鲁棒性,达到理想的控制效果。但原有方法应用对象简单,若应用于多输入多输出(multiple input multiple output,MIMO)系统时,会对控制阵和切换函数矩阵有所限制,要求标称方程中的控制阵正定,且采用原有控制器不能达到理想的效果,在无人机着舰系统中的应用受限。为此,本文提出一种新的积分滑模控制器设计方法,利用Lyapunov理论分析其稳定性,并通过仿真验证该方法的正确性和有效性。

另一方面,由于海面风速及甲板区紊乱流场的影响,恶劣的着舰环境对无人机控制系统抗干扰能力提出更高的要求[14]。为抑制舰尾流等干扰因素的影响,同时消除滑模抖动,引入自适应模糊网络,对积分滑模切换项进行模糊逼近,可去除对外部干扰不确定上界的先验要求,且有效降低舵面抖动。

研究中假定无人机着舰回收方式为撞网回收,以国外现役某小型舰载无人机为对象,构建基于积分自适应模糊滑模控制的无人机自动着舰系统,完成中各模块的分析和设计,通过仿真验证无人机着舰性能。

1无人机自动着舰系统

无人机自动着舰引导系统的结构配置如图1所示,包含飞机动力学和运动学、飞控系统、轨迹控制器等环节。其中Puav0为初始时刻位置矢量,Perr为飞机实际飞行轨迹与理想轨迹的偏差信号。为纵向通道的俯仰控制指令,Δφc为横侧向通道的滚转控制指令,Δδe,ΔδT为飞控系统输出的升降舵和油门偏转量,Δδa,Δδr为副翼舵和方向舵偏转量,外界干扰包括舰尾流、舰运动、导航误差等影响因素。

根据无人机当前的位置信息Puav,计算位置误差Perr。将误差信号引入轨迹控制器,通过引导律计算,给出控制指令Δθc，Δφc,飞控系统接收该指令后,操纵飞机不断修正姿态和航迹,最终消除位置偏差,引导无人机沿理想轨迹着舰。

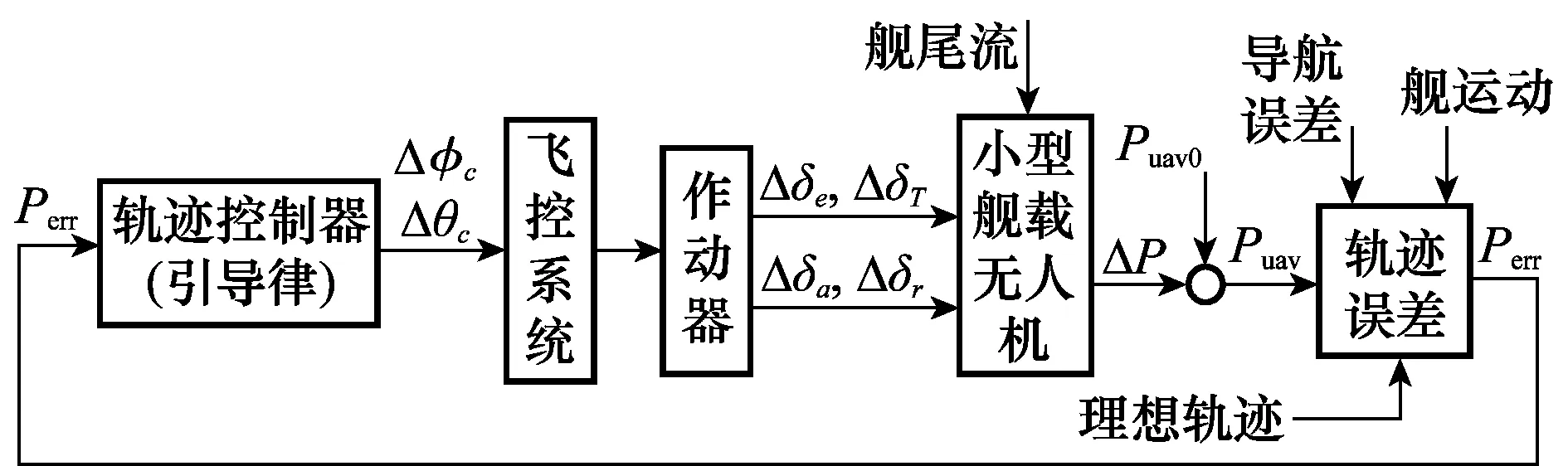
图1　自适应模糊系统网络结构图

2自动着舰飞行控制系统设计

2.1积分滑模飞行控制律设计

无人机状态向量为

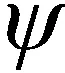
在气流坐标轴系上建立力方程组,在机体坐标轴系上建立力矩方程组和运动学方程组[15],可得到无人机状态向量的12个非线性微分方程组,随后以舰载无人机进场时定常直线飞行状态为基准点进行配平及线性化,可得到无人机纵向和横侧向动力学方程。

由此,含有不确定因素的舰载无人机动力学方程可表示为

(1)

式中,x为状态变量;u为控制变量;纵向运动x=[uwqθ]T;u=[δeδT]T；横向运动x=[vprφ]T;u=[δaδr]T;δe,δT,δa,δr分别为升降舵、油门、副翼舵、方向舵控制量;A，B，D为常值矩阵,且B为满秩,(A,B)可控;ΔA表示状态变量不确定因素的线性部分;f(t,x)表示与状态变量有关的不确定因素的非线性部分;ΔB表示输入的不确定部分;Dw(t)表示外界干扰,假定w(t)有界,且‖w(t)‖≤ε,‖·‖为向量的欧氏范数。

假设 1矩阵ΔA,ΔB和D满足下列匹配条件[16]:

rank[B⋮ΔA]=rank[B⋮ΔB]=

rank[B⋮D]=rank[B]

(2)

根据B的广义逆矩阵B+=(BTB)-1BT,可得

(3)

令

v=Hx+Eu+Fw+g(x,t)

(4)

代入式(1),系统可变为

(5)

并定义

(6)

至此,控制的目标可描述为:针对式(4)、式(5)所示的系统,设计滑模跟踪控制律uc,实现对期望姿态的大范围渐近稳定跟踪。

设计积分切换型函数为

(7)

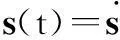
设计如下变结构控制器:

(8)

式中,σij,ωij为常系数;R和δ为对角阵,且元素为ri和δi;sgn(s)=[sgn(s1),sgn(s2),…，sgn(sm)]T。

所设计的控制器采用的均为一般矩阵数值计算,没有特别复杂的运算过程,工程上易于实现。控制器包含三部分,标称模型控制律ue q,不确定模型控制律uNL和干扰补偿控制律uR。

令|ε|=[|ε1|,|ε2|,…,|εm|]T,|g(t,x)|=G|x|,gij为正常数。|x|=[|x1|,|x2|,…,|xn|]T,‖(I+E)-1‖=1/‖I+E‖=1/(1+μ)。

定理 1如果采用控制律(8),则闭环系统(5)稳定,跟踪误差在有限时间内收敛到零。

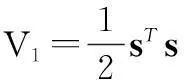
sT[CAx(t)+CBHx(t)+CB(I+E)u(t)+

CBFw(t)+CBg(t,x)-CAx(t)-CBKx(t)]≤

sT[CBHx(t)-RMx(t)-δsgn(s)+CBF|ε|+CBG|x|]=

若能满足下列条件:

(9)

证毕

结论 1对于式(4)和式(5)所示的系统,若满足式(9),则在式(8)所示的积分滑模控制律作用下,在有限时间后,系统状态始终处于相应的滑模面上,即对于t∈[0,∞),有s(t)=0成立。

2.2积分自适应模糊滑模飞行控制律设计

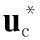
(10)

模糊系统采用由IF-THEN形式的模糊规则构成

其中,n为si导数阶数。

采用乘积推理机、单值模糊器和中心平均解模糊器,模糊系统的输出为

(11)

引入向量ξ(x),令ξ(x)=(ξ1,ξ2,…,ξN)T,

(12)

图2　自适应模糊系统网络结构图

定义最优参数为

(13)

式(13)表示使目标函数取最小值时的变量值,Ωh为φh的集合。

令

设计自适应控制律为

(14)

定理 2如果采用控制律式(10),且由自适应律式(14)进行调节,则闭环系统稳定,跟踪误差在有限时间内收敛到零。

证明定义Lyapunov函数

(15)

若满足

(16)

则

由此,可设计纵向系统跟踪误差方程为

(17)

(18)

飞行控制律为

(19)

积分切换函数为

(20)

横侧向系统与纵向系统结构一致,参数不同,此处不再赘述。

3自动着舰系统仿真评估

3.1自动着舰飞控系统仿真验证

在自动着舰技术领域的研究中,大多采用有人驾驶的舰载机或陆基无人机为模型进行设计和仿真[17-19],本文以国外现役某小型舰载无人机为例[5],建立其全向非线性动力学和运动学模型,随后,以舰载无人机进场时定常直线飞行状态为基准点进行配平及线性化,得到该型无人机纵向和横侧向标称运动方程。

下面详细阐述舰载无人机纵向系统,横侧向系统不再赘述。

令

式中,ΔA,ΔB为不确定矩阵,其元素为随机值。由式(3)可确定E和H的值,G和F的选择参见表1。

表1　飞控系统参数设计表

最后,纵向系统不确定值、外界干扰设置值及控制器参数如表1所示,未加入自适应模糊的控制系统以Mode1表示(即控制律采用式(8)),加入后的系统以Mode2表示(即控制律采用式(10))。

此外,着舰时要求飞机跟踪理想下滑轨迹,本文采用含有σ-β滤波的轨迹控制器,纵向系统的运动学方程如下:

(21)

设计的引导律为

(22)

参数设计如下:

kc=2,kI=0,kP=0.600,kD=1.5

侧向系统参数选取方法如纵向,此处不再赘述。

为验证自动着舰飞行控制系统的跟踪性能,令Mode1和Mode2系统跟踪理想下滑斜坡指令,并在100s处叠加正弦信号8sin0.5 t。下滑角γ0=3.5°,初始高度h0=800m,外界干扰为正弦信号sint。仿真结果表明,无论Mode1,还是Mode2,所设计的系统均能快速准确地跟踪指令，如图3~图6所示。

图3　参考指令下纵向飞控系统跟踪响应曲线

图4　参考指令下Mode2系统各状态变量响应曲线

图5　参考指令下Mode2自适应模糊系统输出值

图6　Mode1 、Mode2纵向舵面响应曲线

图3给出了参考指令下基于积分自适应模糊滑模的控制系统(Mode2)的跟踪曲线,并与经典控制方法进行对比。可以发现,相比于传统PID控制方法,Mode2响应时间快,过渡过程短,跟踪误差小,抗干扰能力强。图4给出了参考指令下Mode2系统各状态变量的响应曲线。图5给出了Mode2系统对外界干扰的估计值。图6给出了同样指令下Mode1和Mode2纵向飞控系统的舵面偏转曲线。从舵面的响应曲线中,可以发现,Mode1中,舵面存在较大的抖动,Mode2有效地削弱了舵面抖动。Mode2系统中控制舵面仍存在微弱抖动,存在小的抖动是允许的。如果抖动频率与对象固有频率不一致,最小消耗能量的抖动能使得飞行器保持“持久”的生命力,从某种意义上增加系统的稳定性。此外,一般的作动器均为一阶或者二阶动力学,可以削弱高频分量,因此,控制信号在经过作动器后可基本接近连续。

3.2基于Mode2的自动着舰系统性能评估

为评估基于Mode2的舰载无人机在各种干扰因素下的着舰性能,构建了如图1所示的无人机自动着舰综合仿真平台。

仿真中加入各种影响因素,在飞控系统中加入舰尾流的影响。通常陆基飞机的大气紊流响应常采用冯.卡尔曼形式或德莱顿形式的紊流模型。由于舰上降落时的特殊大气情况,MIL-F-8785C军用规范给出了特定的大气扰动数学模型[20]。总的舰尾大气扰动各向分量由4大部分组成:随机自由大气紊流分量,尾流稳态分量(雄鸡尾流),尾流的周期性分量,尾流的随机分量。图7给出了总的水平和垂向扰动分量ud、wd。

图7　舰尾大气扰动纵向分量仿真结果

外界干扰即舰尾流的影响可如式(23)所示:

(23)

在飞行轨迹计算中加入导航误差,在着舰前约12.5 s要求飞机跟踪甲板运动,在理想轨迹中加入舰运动学。舰运动学及导航误差模型参考美国海军航空兵武器系统部提供的数据[6],3种常见海况下舰运动对理想着舰点垂直方向位移的总体影响如图8所示,仿真选取海况状态为“海况4”,导航误差的仿真结果如图9所示。

飞行控制器设计参数如3.1节所述。仿真初始条件如下:航母前进速度Vs=15m/s,下滑角γ0=3.5°,飞机前进速度大小为指令速度Va=25m/s。 图10给出了海况4下,基于Mode2的某次着舰纵向跟踪曲线图,图11给出了海况4下,基于传统PID控制的某次着舰纵向跟踪曲线图。从图中可以看出,相比于传统PID控制,基于Mode2的自动着舰系统降低了着舰误差,提高了着舰精度。

图8　舰运动引起的着舰点的垂直偏差

图9　导航误差仿真结果

图10　基于Mode2的某次着舰纵向跟踪曲线图

图11　基于PID控制的某次着舰纵向跟踪曲线图

为评估着舰性能,针对Mode2自动着舰系统,运行近500次仿真,表2给出了不同干扰因素影响下的着舰性能。其中,Seastate4表示加入海况4;Nav表示加入导航误差;Airwake表示加入舰尾流。

由表2可以看出，仅由海况影响的着舰平均误差和标准偏差较小,加入导航误差后,对着舰性能的影响较小,基本可以忽略。舰尾流对着舰性能影响较大,平均误差和标准偏差显著增加。此外,数值仿真表明,在这3种着舰条件下,平均误差和标准差均能符合自动着舰回收的规范[4-5]。

图12分别给出了海况4下,加入舰尾流和导航误差后,基于Mode2和PID控制系统的着舰点分布图。由仿真结果可以看出，基于Mode2的自动着舰系统的着舰点分布较为集中,平均误差和标准偏差较小。

表2　不同干扰因素下着舰性能分析

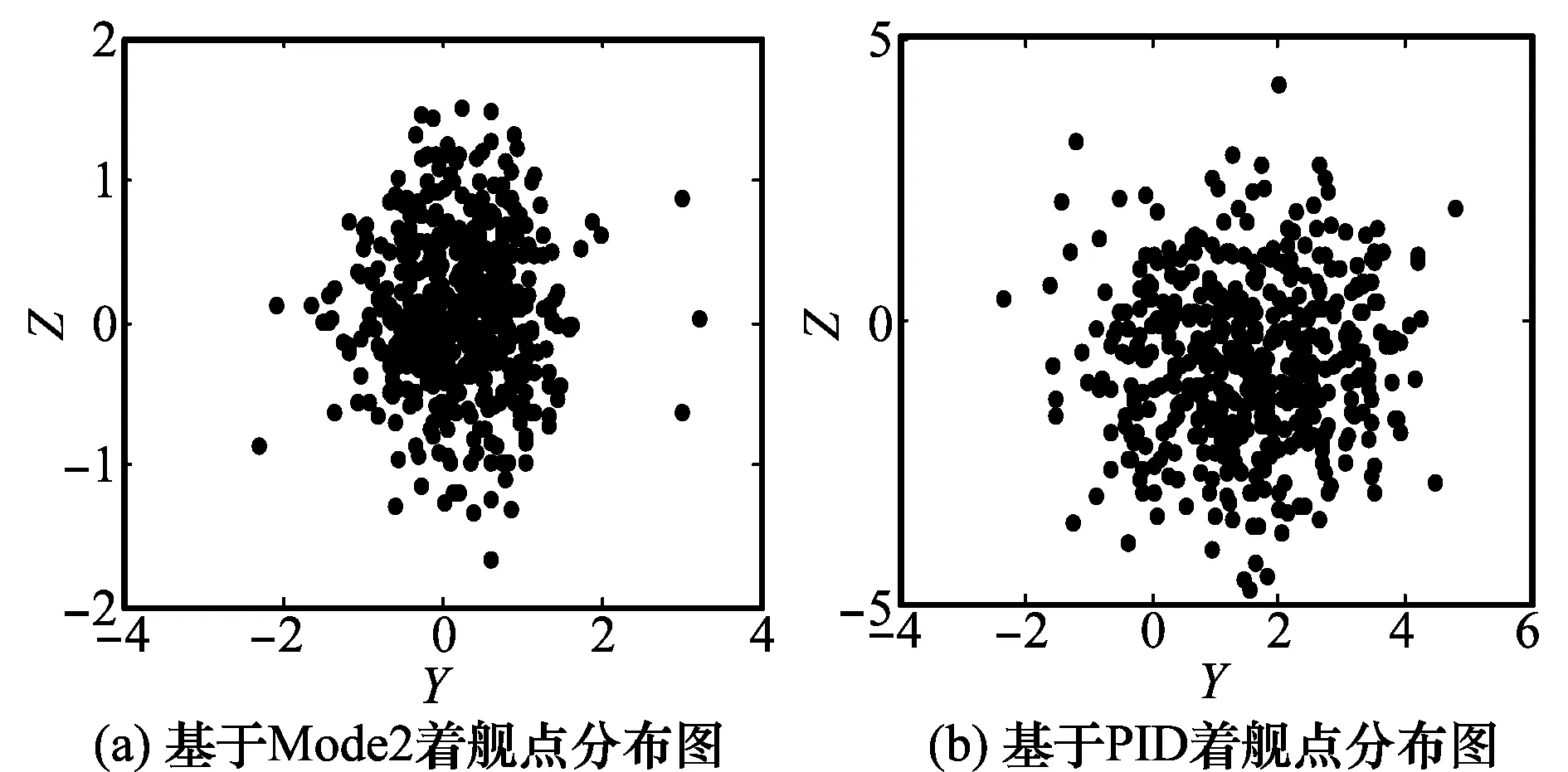
图12　无人机着舰点在回收网上的分布图(YZ平面)

4结论

针对着舰的复杂环境,提出了一种新的基于积分滑模控制与自适应模糊系统相结合的智能飞行姿态控制方法,克服了对原有积分切换函数控制阵和切换函数矩阵的限制。同时,引入自适应模糊网络,对积分滑模切换项进行模糊逼近,且无需预估不确定系统的上界,能削弱控制舵面的抖动。数值仿真验证了该控制方法具有较好的控制精度和鲁棒性。搭建了舰载无人机自动着舰系统,完成各模块的设计和仿真。综合仿真结果表明在积分滑模自动着舰系统作用下,舰载无人机的着舰终端平均误差和标准偏差均能符合性能指标要求,且相较于传统的PID控制技术,其着舰精度和性能得到显著提高。

参考文献：

[1] Zotov V, Gao X. Intermediate carriers for UAV swarms: problem of fleet composition[J].SystemsEngineeringandElectronics, 2013, 24(1): 101-107.

[2] Guo Q, Zhang W, Zhang Y Z, et al. Accurate landing glide path control system of carrier-based UAV and its flight test[J].FlightDynamics, 2012, 30(5): 448-453.

[3] Wenzel K E, Masselli A, Zell A. Automatic take off, tracking and landing of a miniature UAV on a moving carrier vehicle[J].JournalofIntelligent&RoboticSystems, 2011, 61(1/4): 221-238.

[4] Lizarraga M I. Autonomous landing system for a UAV[D]. Monterey: Naval Postgraduate School, 2004.

[5] Fitzgerald P. Flight control system design for autonomous UAV carrier landing[D]. Cranfield: Cranfield University, 2005.

[6] Sweger J F. Design specifications development for unmanned aircraft carrier landings[R]. Maryland:United States Naval Academy Annapolis, 2003.

[7] Denison N A. Automated carrier landing of an unmanned combat aerial vehicle using dynamic inversion[D]. Ensign:The Air Force University, 2007.

[8] De Lellis E, Di Vito V, Ruby M, et al. Adaptive algorithm for fixed wing UAV autolanding on aircraft carrier[C]∥Proc.oftheAIAAGuidance,Navigation,andControlCo-locatedConferences, 2013.

[9] Sun Y, Zhang W G, Zhang M. Adaptive sliding mode high maneuvers flight control based on backstepping procedure[J].ControlandDecision,2011,26(9):1377-1381.(孙勇,章卫国,章萌.基于反步法的自适应模糊大机动飞行控制[J].控制与决策,2011,26(9):1377-1381.)

[10] Yang I, Kim D, Lee D. A flight control strategy using robust dynamic inversion based on sliding mode control[C]∥Proc.oftheAIAAGuidance,Navigation,andControlConferences, 2012.

[11] Liu M, Zhang L, Shi P, et al. Robust control for stochastic system against bounded disturbances with application to flight control[J].IEEETrans.onIndustrialElectronics, 2014, 61(3): 1504-1515.

[12] Hamayun M T, Edwards C, Alwi H. Augmentation scheme for fault-tolerant control using integral sliding modes[J].IEEETrans.onControlSystemsTechnology,2014,22(1):307-313.

[13] Lin F J, Chou W D. An induction motor servo drive using sliding-mode controller with genetic algorithm[J].ElectricPowerSystemsResearch, 2003,64(2): 93-108.

[14] Wong F, Gagnon E, McTaggart K, et al. A parametric study of factors affecting successful ship recovery of UAVs[R]. Valcartier: Defence R&D, 2008.

[15] Zhang L Z. Design on autonomous flight control system[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2011.(张立珍. 无人机自主飞行控制系统的设计[D]. 南京:南京航空航天大学, 2011.)

[16] Gao W B.Variablestructurecontroltheoryanddesignmethod[M]. Beijing: Science Press, 1996.(高为炳.变结构控制的理论及设计方法[M].北京:科学出版社,1996.)

[17] Urnes J M, Hess R K. Integrated flight control systems development—the F/A-18A automatic carrier landing system[C]∥Proc.oftheGuidanceandControlConference,1983:920-930.

[18] Sousa P, Wellons L, Colby G, et al, Test results of an F/A-18 automatic carrier landing using shipboard relative global positioning system[R]. Patuxent River, MD: Naval Air Warfare Center Aircraft Division, 2003.

[19] Deng J, Yan Z P, Ai J L. Application of guzzy control technology to automatic carrier landing system[J].JournalofSystemSimulation, 2012,24(3):645-650.(邓娟,颜振萍,艾剑良.模糊控制技术在自动着舰控制系统中的应用[J].系统仿真学报,2012,24(3):645-650.)

[20] Jiao X. Research on carrier-based aircraft landing condition and wave-off decision technology[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011.(焦鑫.舰载机着舰环境与复飞决策技术研究[D].南京: 南京航空航天大学，2011.)

郑峰婴(1981-),女,助理研究员,博士研究生,主要研究方向为飞行器控制技术、舰载机着舰技术。

E-mail:zhfy@nuaa.edu.cn

龚华军(1965-),男,教授,博士,主要研究方向为飞行器控制技术、光传飞行控制技术、舰载机着舰技术。

E-mail:ghj301@nuaa.edu.cn

甄子洋(1980-),男,副教授,博士,主要研究方向为飞行器自主飞行控制以及编队协同控制、信息融合控制。

E-mail:zhenziyang@nuaa.edu.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150106.1158.002.html

Carrier UAV autonomous landing system based on

integral sliding mode control

ZHENG Feng-ying1, GONG Hua-jun2, ZHEN Zi-yang2

(1.CollegeofAstronautics,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China;

2.CollegeofAutomationEngineering,NanjingUniversityofAeronauticsand

Astronautics,Nanjing210016,China)

Abstract:To overcome the adverse effects of various disturbances on unmanned aerial vehicle (UAV) landing, a new sliding mode control method from the point of engineering realization is proposed to avoid restrictions in the traditional integral sliding mode, and the adaptive fuzzy system is used to offset interference errors.The sliding switching is approximated to effectively reduce chattering. Finally, an autonomous landing simulation platform is built. Take an active service small carrier UAV as the research object, and the results of the simulation indicate that this system can effectively overcome various factors affecting landing,such as sea state, navigation error, airwake, realizing the UAV safe landing, and the landing performances meet the design requirements.

Keywords:carrier unmanned aerial vehicle (UAV); autonomous landing; flight control; integral sliding; adaptive fuzzy

作者简介：

中图分类号：V 249.1

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2015.07.23

基金项目：国家自然科学基金(61304223)；航空基金(2013ZA52002)；高等学校博士学科点专项科研基金(20123218120015)资助课题

收稿日期：2014-05-18；修回日期：2014-11-17；网络优先出版日期：2015-01-06。