基于自抗扰的反步滑模制导控制一体化设计

董朝阳, 程昊宇, 王　青

(1. 北京航空航天大学航空科学与工程学院, 北京 100191;

2. 北京航空航天大学自动化科学与电气工程学院, 北京 100191)



基于自抗扰的反步滑模制导控制一体化设计

董朝阳1, 程昊宇1, 王青2

(1. 北京航空航天大学航空科学与工程学院, 北京 100191;

2. 北京航空航天大学自动化科学与电气工程学院, 北京 100191)

摘要：针对导弹末制导段的制导控制问题,基于自抗扰控制和反演终端滑模控制,提出了一种导弹制导控制一体化设计算法。利用块严格反馈系统描述一体化模型,将存在的模型误差、目标机动等看做未知干扰。采用扩张状态观测器对系统不确定性和干扰进行估计和补偿。设计反步终端滑模控制方法实现导弹的姿态控制。仿真证明了设计的一体化算法可以获得较小的脱靶量,系统对存在的内外干扰和不确定性具有较强的鲁棒性。

关键词：制导控制一体化;自抗扰控制;扩张状态观测器;反步终端滑模

0引言

传统的导弹制导控制系统设计方法是将控制和制导回路分开设计,首先设计制导回路获取期望过载,然后将设计好的控制器嵌入到制导回路中进行联调,使导弹尽可能快地跟踪制导回路的期望过载,这种方法只利用各自回路的信息,没有考虑其耦合关系。制导控制一体化方法[1-4]不再严格区分制导回路和控制回路,充分利用制导和控制回路之间的耦合关系,根据弹目相对运动信息与导弹自身信息直接产生控制指令,在舵偏的反馈设计中使用了姿态、视线角速度等综合信息[5],提高了制导精度和系统可靠性。

制导控制一体化(integrated guidance and control, IGC)方法在20世纪80年代提出,国内外很多学者已经对此进行了大量的研究。现有文献中一体化设计所采用的主要方法有最优控制[6]、滑模控制[7-13]、自适应控制[14-15]、反馈线性化[16]等。文献[6]采用θ-D的次优控制方法,近似求解Hamilton-Jacobi-Bellman方程,得到该最优控制的近似最优解,但是忽略了未建模因素和扰动对系统的影响。文献[11]利用反步滑模方法研究了网络环境下制导控制一体化算法的设计问题,但是没有考虑系统不确定性和外部干扰的影响。文献[12]利用模糊反步滑模设计了制导控制一体化系统,但是算法数学过程繁琐,工程应用受到了一定限制。文献[14]通过反演设计方法得到虚拟控制指令和舵偏指令,但是需要假设不确定有界,由于实际中不确定项与系统状态有关,所以预先确定其定常上界比较困难。

导弹飞行过程中,气动力参数和气动力矩参数均为状态量的复杂不确定函数,并且实际中风速、大气密度和目标机动都存在不确定性。自抗扰控制[17-18]利用扩张状态观测器可以直接对系统内部不确定动态进行实时估计和补偿,因而不需要精确的模型信息,也不需要假设不确定模型为参数线性化或有界,而且算法结构简单,适合工程应用。文献[18]利用自抗扰技术研究了导弹的IGC问题,但是依然属于传统的制导控制系统分离设计,通过设计制导律获得期望的过载,然后设计控制器使导弹能够跟踪期望过载。

基于以上分析,本文针对存在不确定性的制导控制一体化模型,通过扩张状态观测器(extended state observer, ESO)将系统中的未建模动态和外部干扰统一扩张成一个新的状态并对其进行估计,通过实时补偿来消除或抑制不确定项的影响,结合反演控制和终端滑模控制,设计IGC算法,保证系统在有限时间内收敛,最后通过仿真验证了IGC算法的正确性和有效性。

1制导控制一体化系统建模

1.1相对运动模型

惯性系下,弹目相对运动模型如图1所示。

图1　弹目相对运动模型

图1中,M和T分别代表导弹和目标;R为弹目相对距离;λ为弹目视线角;γM和γT分别为导弹和目标的航迹倾角;VM和VT分别为导弹和目标的速度。根据图1所示,导弹和目标在纵向平面内的相对运动方程为

(1)

(2)

对式(2)求导并将式(1)代入式(2)得

(3)

(4)

式中

其中，P为导弹发动机推力;α为攻角;Y为升力。

为保证击中目标,应设计制导控制系统使得Vr=0。

1.2导弹动力学模型

本文采用如下所示导弹纵向动力学模型[19]:

(5)

(6)

(7)

(8)

式中,Jz为导弹对z轴的转动惯量;ωz为俯仰角速率;ϑ为俯仰角;m为导弹的质量;δz为舵偏角;Mδz为舵偏角引起的俯仰力矩;M0=M0(α,M,h,Vt,ωz)为攻角、马赫数和高度等因素引起的力矩,M0可近似写为 M0=Mαα+Mωzωz。

当α,ωz和升降舵偏δz较小时,Y和Mz可写为

针对轨控式导弹,结合其特点,对系统作如下假设:

假设 1由于舵面面积小,并且舵面下洗,舵面偏转对升力的影响较小,即cδzy≈0。

假设 2末制导阶段导弹速度VM认为是常值。

假设 3末制导阶段导弹主发动机停止工作,即P=0[12]。

由以上分析,可以建立制导控制一体化模型如下所示:

(9)

(10)

(11)

式中,dVq,dα,dωz为系统存在的未知不确定项。

(12)

式中

2制导控制一体化算法设计

制导控制系统设计的目标是控制x1收敛至零,并且对于模型不确定性和外界干扰具有较强的鲁棒性。本文利用扩张状态观测器对系统不确定性和干扰进行补偿,提高系统的鲁棒性,利用反演终端滑模控制方法对一体化系统进行控制,分3步设计一体化系统。

步骤 1考虑闭环系统(14)的第1个子系统

(13)

定义子系统1的误差:e1=x1-x1r，其中,x1r为子系统1的指令信号,将其对时间求导可得

(14)

在实际中,d1为未知干扰,采用扩张状态观测器对存在的未知干扰进行估计[19],将d1视为扩张状态,则系统(13)为

(15)

式中，x1d为干扰的扩张状态；v1(t)为干扰的微分,也为未知函数。设计如下所示的二阶扩张状态观测器[20]:

式中,E11为ESO的估计误差;Z11和Z12分别为状态量和干扰的估计值;β11和β12为观测器增益。函数fal(·)定义为

定义子系统1的观测误差:ε1=Z12-d1。

观测器的动态误差方程可以表示为

(16a)

(16b)

当观测器稳定时,误差向量的微分满足

(17)

将式(17)代入式(16)可得

当|E11|>δ时,误差的估计值可以表示为

当|E11|<δ时,误差的估计值可以表示为

观测器的误差由参数β11,β12,μ1,δ1决定,可以选择β11>0,β12>0,0<μ1<1,δ1>0,令β12足够大,使得|v1/β12|尽量小,令β11足够小从而使得ε1尽量小,而且μ1越小,测量的误差信号越平稳,从上述分析可以看出,通过合理选择扩张状态观测器的参数,可以使得E11和ε1收敛到零很小的邻域内,从而准确地估计出系统的状态和干扰。扩张状态观测器的收敛性在文献[21-22]中已得到证明。

通过以上分析,对观测器作如下假设:

得到干扰的估计值后,设计如下虚拟控制量:

(18)

为了避免下一步设计中对虚拟控制律求导,采用动态面方法[23]设计如下一阶低通滤波器对虚拟控制信号进行滤波:

(19)

第1个子系统的边界层误差为

(20)

由式(19)可得

对式(20)求导并将上式代入可得

(21)

(22)

由式(22)可得

(23)

由式(21)和式(23)可得

定义第2个子系统的跟踪误差为

从而可得第1个系统的误差方程为

(24)

定义子系统1的Lyapunov函数为

(25)

对V1求导并将式(24)代入可得

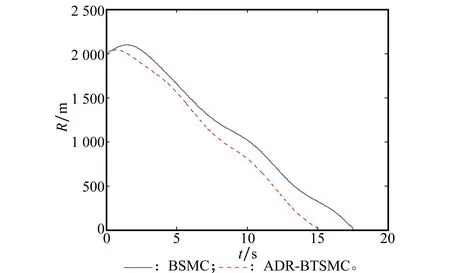
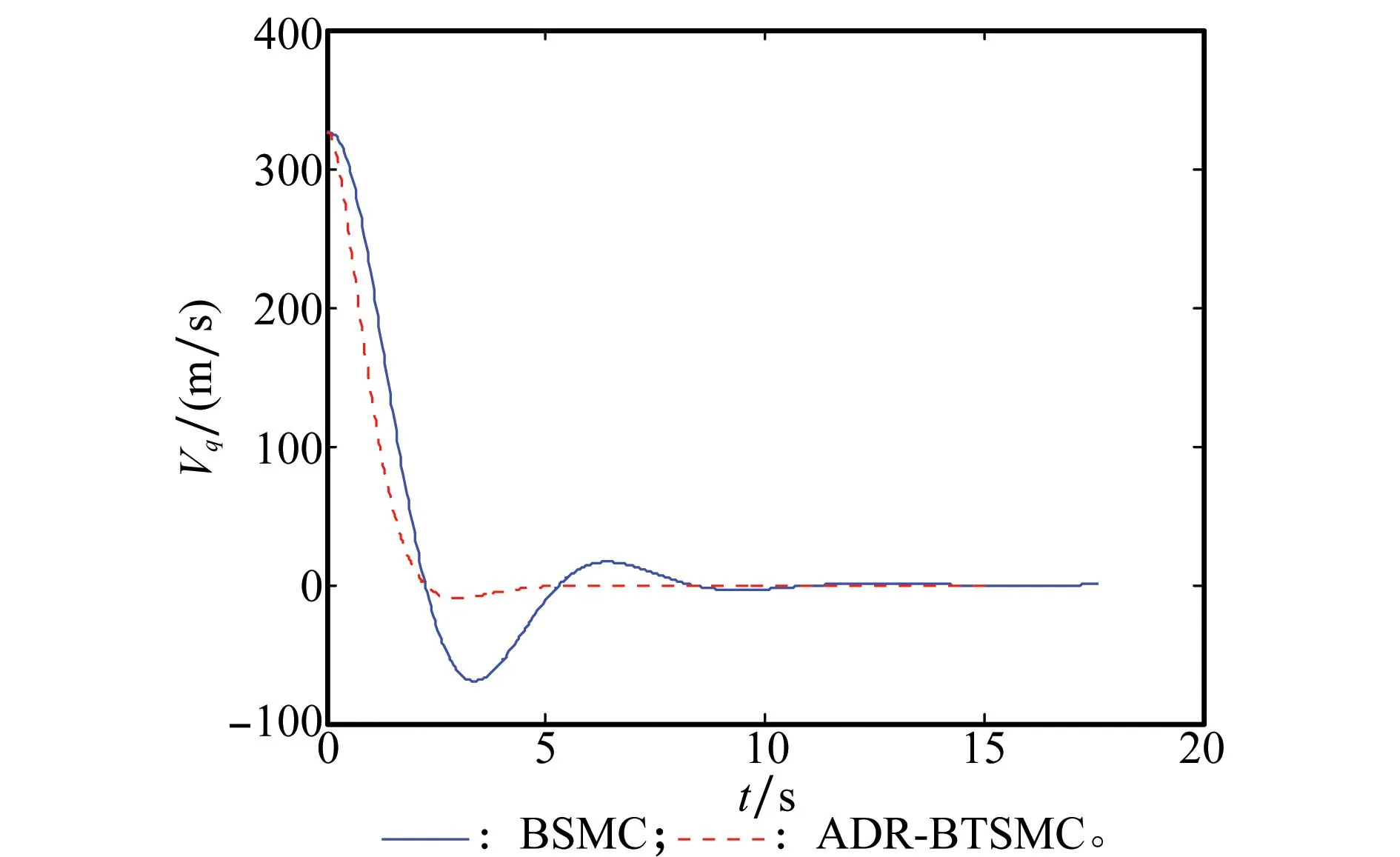
由Young不等式ab

则子系统1的Lyapunov函数满足

(26)

步骤 2考虑闭环系统的第2个子系统:

对e2求导得

采用如下ESO对干扰进行估计:

式中,E21为ESO的估计误差;Z21和Z22分别为状态量和干扰的估计值;β21和β22为观测器增益。

设子系统2的观测误差为:ε2=Z22-d2,假设观测器误差ε2

设计如下虚拟控制量:

采用如下低通滤波器对虚拟控制量进行滤波:

(27)

设第2个虚拟控制量的滤波误差为

(28)

与步骤1类似,可以得到

定义第3个子系统的跟踪误差为

从而第2个子系统的误差方程可以写为

定义子系统2的Lyapunov函数为

(29)

对V2求导,采用类似步骤1中的步骤和方法,可得

(30)

经过前两步的设计,得到2个期望虚拟控制,设计控制律使得e3收敛到零,则有

(31)

其中，定义κ和c为如下所示的正常数:

由式(31)可知

由上述分析可知,如果设计控制律使状态跟踪误差e3收敛到零,可以保证子系统1,子系统2的状态半全局一致有界,系统的跟踪误差收敛,从而可以得出闭环系统是稳定的。

步骤 3考虑闭环系统的第3个子系统

采用如下ESO对干扰进行估计:

式中,E31为ESO的估计误差;Z31和Z32分别为状态量和干扰的估计值;β31和β32为观测器增益。

则子系统3的观测误差为:ε3=Z32-d3。

设观测器误差ε3

(32)

式中,γ>0,p和q为正奇数,且1

(33)

当t>tr时,系统保持在二阶滑动模态。由式(33)可知,可以通过选择参数p,q,γ可以调节系统的收敛速度。

定理 1对于存在干扰和不确定性的系统(12),选取非奇异终端滑模面(32),并设计如下控制律:

u=u1+u2

(34a)

(34b)

(34c)

其中,sig定义如式(35)所示,表示Sigmoid函数,引入Sigmoid函数可以减小滑模控制引起的抖振

(35)

式中,a>0为设计常数,其大小直接决定Sigmoid函数的收敛速度。

证明对于子系统3,定义Lyapunov函数为

对其按时间求导可得

(36)

将e3对时间求导可得

将e3再次对时间求导可得

(37)

将u2代入式(37)可得

(38)

将式(38)代入式(36)可得

(39)

当e3收敛到零时,式(31)成立,对式(31)两边同时乘以eκ t可得

(40)

则式(40)两边同时对t积分得

(41)

证毕

3仿真算例

为了对本文提出的制导控制一体化算法进行验证,本节采用如下模型进行仿真。

假设导弹和目标在铅垂面内运动,导弹的速度VM=760 m/s,导弹的初始弹道倾角γM(0),攻角α(0)和俯仰角速率ωz(0)均为0,导弹初始坐标xM(0)=0,yM(0)=0;目标速度VT=440 m/s,目标初始坐标xT(0)=0,yT(0)=2 000。导弹标称情况下各气动系数为

滤波器时间常数τ1=τ2=0.01 s,一体化设计的目标是使视线角速率收敛为零,所以系统指令信号x1r=0。假设舵机为模型为时间常数为0.01 s的一阶惯性环节且限幅为±30°。

控制器参数k1=5,k2=8,ρ1=20,ρ2=50,ρ3=10,终端滑模面设计参数为p=5,q=3,γ=0.01,扩张状态观测器设计参数为

为了进行仿真对比研究。本文分别采用反步滑模方法和自抗扰反步终端滑模方法在标称情况下,以及目标作幅值为5g的正弦机动,气动参数摄动±30%,外部干扰d2=0.1 sin(t),d3=0.2 sin(t)的情况下进行仿真验证。限于篇幅限制,此处省略标称情况下的仿真曲线。两种情况下的脱靶量和拦截时间对比结果如表1所示,其中,BSMC(backstepping sliding mode control)代表反步滑模控制,ADR-BTSMC(active disturbance rejection-backstepping terminal sliding mode control)代表自抗扰反步终端控制;存在不确定性情况下的仿真结果如图2～图9所示。

表1　两种方案下的仿真结果

图2　弹目相对距离变化图

图3　导弹俯仰舵偏变化图

图4　视线角速率变化图

图5　导弹攻角变化图

图6　导弹俯仰角速度变化图

图7　视线角速率的实际值与估计值

图8　攻角的实际值与估计值

图9　俯仰角速率的实际值与估计值

图2为弹目相对距离图,从图中可以看出,本文提出的方法可以更快对目标进行拦截,且弹道更为理想;图3说明了本文采用方法所需要的舵偏角较小,且在过渡过程的动态响应更为平缓,保证了执行机构输出有界,避免了饱和与振荡的现象;图4说明了视线角速率可以快速收敛至零且具有更好的动态特性,确保了导弹对目标的精确打击;图5～图6为攻角、俯仰角速度的响应曲线,表明攻角和俯仰角速度均能满足实际系统约束;从图7～图9可以看出,ESO准确有效地对系统状态进行了估计。

从表1可以看出,本文的IGC算法可以获得较小的脱靶量和较短的拦截时间,确保了对目标的快速精确打击。

基于以上分析,在目标机动,存在参数摄动及外部干扰的情况下,采用自抗扰反步终端滑模方法,导弹可以快速精确击中目标,系统具有较好的鲁棒性、动态性能和制导精度。

4结论

针对导弹在外干扰和不确定性影响下的制导控制一体化设计问题,提出了一种自抗扰反步终端滑模方法。设计ESO对系统中的不确定项和干扰进行估计和补偿,并利用反演终端滑模方法设计控制器,保证误差在有限时间内收敛,仿真结果表明,本文设计的IGC算法可以有效克服干扰对系统的影响,保证系统具有较好的鲁棒性,动态性能和较高的制导精度。

参考文献：

[1] Shtessel Y B, Shkolnikov I A. Levant A. Smooth second-order sliding modes: missile guidance application[J].Automatica, 2007, 43(8): 1470-1476.

[2] Hou M Z, Liang X L, Duan G R. Adaptive block dynamic surface control for integrated missile guidance and autopilot[J].ChineseJournalofAeronautics, 2013, 26(3): 741-750.

[3] Maital L, Tal S, Shual G. Linear quadratic integrated versus separated autopilot-guidance design[J].JournalofGuidance,Control,andDynamics, 2013, 36(6):1722-1730.

[4] Dong F Y, Lei H M, Zhou C J, et al. Research of integrated robust high order sliding mode guidance and control for missiles[J].ActaAeronauticaletAstronauticsSinica, 2013, 34(9): 2212-2218.(董飞垚, 雷虎民, 周池军, 等. 导弹鲁棒高阶滑模制导控制一体化研究[J].航空学报, 2013, 34(9): 2212-2218.)

[5] Xue W C, Huang C D, Huang Y. Design methods for the integrated guidance and control system[J].ControlTheory&Applications,2013,30(12):1511-1520.(薛文超,黄朝东,黄一.飞行制导控制一体化设计方法综述[J].控制理论与应用,2013,30(12):1511-1520.)

[6] Xin M, Balakrishnan S N, Ohlmeyyer E J. Integrated guidance and control of missiles with θ-D method[J].IEEETrans.onControlSystemsTechnology, 2006, 14(6):981-992.

[7] Yeh F K, Cheng K Y, Fu L C. Variable structure-based nonlinear missile guidance/autopilot design with highly maneuverable actuators[J].IEEETrans.onControlSystemsTechnology, 2004, 12(6): 944-949.

[8] Yamasaki T, Balakrishnan S N, Takano H. Separate-channel integrated guidance and autopilot for automatic path-following[J].JournalofGuidance,Control,andDynamics,2013,36(1):25-34.

[9] Shima T, Idan M, Golan O M. Sliding mode control for integrated missile autopilot-guidance[J].JournalofGuidance,Control,andDynamics, 2006, 29(2): 250-260.

[10] Idan M, Shima T, Golan O M. Integrated sliding mode autopilot-guidance for dual-control missiles[J].JournalofGuidance,Control,andDynamics, 2007, 30(4): 1081-1089.

[11] Wang Q, Qi C D, Dong C Y. Integrated guidance and control design for a class of missile with networked packet dropouts[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2014, 40(6): 721-726.(王青, 祁成东, 董朝阳. 存在网络丢包的导弹制导控制一体化设计[J].北京航空航天大学学报, 2014, 40(6):721-726.)

[12] Ran M P, Wang Q, Hou D L, et al. Backstepping design of missile guidance and control based on adaptive fuzzy sliding mode control[J].ChineseJournalofAeronautics,2014,27(3):634-642.

[13] Hu J B, Li F, Wei G L, et al, Theory and applications of backstepping sliding mode variable structure control for uncertain systems[J].SystemsEngineeringandElectronics,2014,36(3):519-526.(胡剑波,李飞,魏高乐,等.不确定系统反推滑模变结构理论及其应用[J].系统工程与电子技术,2014,36(3):519-526.)

[14] Choi J Y, Chwa D Y. Adaptive nonlinear guidance considering target uncertainties and control loop dynamics[J].IEEETrans.onAerospaceandElectronicSystems,2003,39(4):1139-1143.

[15] Chwa D Y, Choi J Y. Observer-based adaptive guidance law considering target uncertainties and control loop dynamics[J].IEEETrans.onControlSystemsTechnology, 2006,14(1):112-123.

[16] Yin Y X, Yang M, Wang Z C. Three-dimensional guidance and control for missile[J].ElectricMachinesandControl,2010,14(3):87-91.(尹永鑫,杨明,王子才.飞行器三维制导控制一体化设计[J].电机与控制学报,2010,14(3):87-91.)

[17] Han J Q. From PID to active disturbance rejection control[J].IEEETrans.onIndustrialElectronics,2009,56(3):900-906.

[18] Zhao C Z, Huang Y. ADRC based integrated guidance and control scheme for the interception of maneuvering targets with desire los angle[C]∥Proc.ofthe29thIEEEChineseControlConference, 2010: 6192-6196.

[19] Stevens B L, Lewis F L.Aircraftcontrolandsimulation[M].New York:Wiley,1992.

[20] Xia Y Q, Zhu Z, Fu M Y. et al. Attitude tracking of rigid spacecraft bounded disturbances[J].IEEETrans.onIndustrialElectronics, 2011, 58(2): 647-659.

[21] Guo B Z, Zhao Z L. On the convergence of an extended state observer for nonlinear systems with uncertainty[J].SystemandControlLetters, 2011, 60:420-430.

[22] Zhu Z, Xu D, Liu J M, et al. Missile guidance law based on extended state observer[J].IEEETrans.onIndustrialElectronics, 2013, 60(12):5882-5891.

[23] Swaroop S, Hedrick J K, Yip P P. et al. Dynamic surface control for a class of nonlinear systems[J].IEEETrans.onAutomaticControl, 2000, 45(10): 1893-1899.

董朝阳(1966-),男,教授,博士研究生导师,主要研究方向为飞行器制导与控制、系统鲁棒性研究和飞行力学。

E-mail: dongchaoyang@buaa.edu.cn

程昊宇(1990-),男,博士研究生,主要研究方向为飞行器制导与控制、系统鲁棒性。

E-mail: chenghaoyu@ase.buaa.edu.cn

王青(1968-),女,教授,博士研究生导师,主要研究方向为导航制导与控制、变结构控制。

E-mail: wangqing@buaa.edu.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150106.1200.004.html

Backstepping sliding mode control for integrated guidance and

control design based on active disturbance rejection

DONG Chao-yang1, CHENG Hao-yu1, WANG Qing2

(1.SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100191,China;

2.SchoolofAutomationScienceandElectricalEngineering,BeihangUniversity,Beijing100191,China)

Abstract:Based on active disturbance rejection control and the backstepping-sliding mode design method, an integrated guidance and control design is proposed for missiles during the terminal course. The integrated model is formulated as a block-strict-feedback nonlinear system, in which modeling errors and target maneuvers are viewed as unknown uncertainties. An extended state observer is developed to estimate and compensate the impact from uncertainties and disturbances. A backstepping-sliding mode controller is proposed to realize the attitude control. Simulation results show that, with the application of the proposed method, small miss distances are achieved, and the system is robust against system uncertainties and disturbances.

Keywords:integrated guidance and control; active disturbance rejection control; extended state observer; backstepping terminal sliding mode

作者简介：

中图分类号：TP 273

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2015.07.21

基金项目：国家自然科学基金(61273083)资助课题

收稿日期：2014-05-30；修回日期：2014-11-14；网络优先出版日期：2015-01-06。