基于改进MOPSO的多级系统备件配置优化研究

王亚彬, 赵建民, 程中华, 王建增

(1.军械工程学院装备指挥与管理系, 河北 石家庄 050003;

2.中国人民解放军66046部队, 河北 石家庄 050000)



基于改进MOPSO的多级系统备件配置优化研究

王亚彬1, 赵建民1, 程中华1, 王建增2

(1.军械工程学院装备指挥与管理系, 河北 石家庄 050003;

2.中国人民解放军66046部队, 河北 石家庄 050000)

摘要：备件是装备保障的重要物质基础,合理规划备件的配置方案是提高装备保障效能的关键。针对多级保障系统备件配置优化的高维、非线性问题,构建了以备件保障度最大、保障费用最小为目标函数,以其他准则为约束条件的优化配置模型。面向优化模型求解的难题,在传统粒子群算法的基础上,提出了一种改进的粒子群求解算法,给出了该算法的设计思路和优化流程,采用基于准则的方法以及改进惯性权重等措施,以两个目标作为引导,在备件配置方案生成时可以避免长时间的无效搜索,提高了粒子群优化算法的求解效率,最后通过算例证明该方法的可行性和有效性。

关键词：多目标粒子群优化方法; 备件; 配置; 优化; 保障度

0引言

备件是装备保障的重要物质基础,是影响装备战备完好性和保障能力的重要因素。备件配置优化是通过备件的合理匹配,使其达到最佳的综合技术经济效益,其本质上是一个资源配置优化的决策过程,因而越来越多的研究人员,采用了系统决策、运筹学、工程经济学等理论进行备件配置优化研究[1]。文献[2]等利用蒙特卡罗仿真、分层边际算法研究了维修过程中备件的配置优化问题;文献[3]分别给出了模拟退火算法、遗传算法及蚁群算法对该类问题的求解;文献[4-5]研究了基于粒子群算法的两级体制下备件配置优化问题;文献[6-7]利用遗传算法对备件储备数量进行了相关研究,构建了优化模型;文献[8]基于METRIC理论对防空武器系统的备件配置进行了优化研究;文献[9]利用马尔可夫模型研究了备件配置优化的方法;文献[10]从体系保障度优化的角度对备件库存方案进行了研究。虽然以上研究都取得了一定的成果,然而它们大多是以单种装备为对象,从单目标角度考虑备件的配置优化问题,实际上,备件配置决策时往往要着眼保障系统整体,针对多种装备,同时考虑备件保障度、保障费用等多个目标。由于各个目标之间关系较为复杂,有的目标之间相互矛盾,有的相互补充,这就使得备件多目标配置优化问题比单目标配置优化问题要复杂的多。

粒子群优化(particle swarm optimization,PSO)算法是一种新兴的基于群体智能理论的演化计算技术,1995年由美国的Eberhart和Kennedy博士提出。多目标粒子群优化方法(multiple objective PSO,MOPSO)与求解单目标PSO方法相比,不同点在于MOPSO需要在各个不同目标之间进行权衡,最终找到一组解。其关键问题是如何确定一个适当的适应度函数,来度量一个解决方案在多目标层面上的质量。根据适应度函数的确定方法,可将求解多目标问题的粒子群算法分为以下3类:一是目标聚合法[11],将多目标函数进行加权聚合,转化为单目标函数进行计算;二是基于帕累托支配的方法[12],将非劣解集中最孤立的非劣解赋给全局极值,从而引导MOPSO方法尽可能的找出分布均匀的非劣解集;三是基于准则的方法[13],该方法不同时考虑所有目标,而是根据优化过程中的不同情况,将适应度函数在不同目标间转化。

本文构建了以备件保障度最大、保障费用最小为目标函数、以其他准则为约束条件的备件多目标优化配置模型;在此基础上,面向多目标约束模型求解的难题,设计了基于准则的粒子群求解算法,并进行了算例分析。

1备件配置优化建模

1.1模型假设

(1) 装备维修分为中继级和基层级两级,在中继级有一个师仓库,在基层级有多团仓库;

(2) 各类型装备对备件的需求相互独立,故障分布为指数分布,备件需求服从泊松分布;

(3) 所有部件故障均会影响系统任务的完成;

(4) 由于预防性维修容易提前预测和安排,而事后维修的随机性较大,所以仅考虑事后维修情况;

(5) 所有故障件都进行换件维修。

备件的配置关系如图1所示,其中装备(k,Nj)中的k表示第k类型装备,Nj表示该型装备的数量。

图1　备件的配置关系

1.2符号说明

为了便于对问题描述,该模型中的常用符号说明如下:

i表示第i种备件;

I表示备件种类数;

J表示保障系统中基层级维修机构数量;

Nj表示第j个基层级单位有某型号装备数量;

K表示所有基层级单位共有某型号装备数量;

Eji表示第j个基层级在规定的装备工作时间内,对备件i的平均需求数量;

Ei表示所有基层级在规定的装备工作时间内,对备件i的平均需求数量;

E[B(Si)]表示所有基层级向中继级请领备件i的平均数量(短缺数量);

E[D(Si,Soi)]表示中继级备件i的平均请领数量(短缺数量);

to表示平均基层级向中继级请领备件的时间;

tm表示平均中继级筹措备件的延迟时间;

Sji表示第j个基层级配备备件i的数量;

Soi表示中继级配置备件i的数量;

P(xji)表示第j个基层级需要备件i的数量为xji的概率;

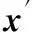
Eoi表示中继级第i类备件的平均需求数量;

Ci表示第i类备件的单价;

Tbfi表示部件i的平均故障间隔时间。

1.3模型构建

(1) 基层级备件需求数

由于P(xji)表示在规定的装备工作时间内,对第j个基层级需要备件i的数量为xji的概率。因此,第j个基层级在规定的装备工作时间内对备件i的平均需求数量为

(1)

(2) 基层级备件短缺率

所有基层级在规定的装备工作时间内,对备件i的平均需求数量Ei可表示为

(2)

所有基层级向中继级请领备件i的平均数量E[B(Si)]可表示为

(3)

式中,第j个基层级的平均短缺数E[B(Sji)]是备件需求数量超过储备数量Sji的平均值,即

(4)

所以,由基层级平均需求数量Ei和平均请领数量E[B(Si)],可以得到备件i在基层级的短缺率为

(5)

(3) 中继级备件短缺率

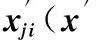
(6)

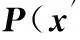
(7)

根据假设条件,第j个库存第i种备件需求数为k的概率P(Xji=k)为

(8)

式中,λji为第j个工作单元第i种备件的需求率；t为装备工作时间。

为计算系统不缺备件的概率,运用泊松分布的性质和随机过程原理,当N=2时,可得

也就是说,对于N=2的情况,备件需求仍然服从泊松分布。假设N=n,该结论成立,对于N=n+1时,与上式相同的分析可得

根据数学归纳原理,可以得出N=n+1时,总的备件需求仍然服从泊松分布。因此,有

(9)

在求得了中继级备件i需求概率的基础上,利用相同的方法,可得中继级备件i的平均需求数量

(10)

中继级的平均请领数量(短缺数量)为

(11)

则中继级备件i的短缺率为

(12)

(4) 基层级备件保障平均延迟时间

基层级备件保障延迟的原因,一是基层级短缺而中继级不短缺;二是基层级和中继级都短缺。因此,基层级备件的平均保障延迟时间为

(13)

(5) 备件i的保障度

假设已知部件i的寿命分布,可以得到该部件的平均故障间隔时间Tbfi,即该部件的平均工作时间,则备件i的稳态保障度为

(14)

整理,得

(15)

以上求得了备件i的保障度,其他备件的保障度可由类似的方法得到。根据文献[14]可知,同型装备上所有备件的保障度可用各备件保障度的乘积表示,即所有备件的保障度可表示为

(16)

(6) 多目标配置优化模型

备件的配置优化模型可以表示为

maxPS=

(17)

(18)

(19)

(20)

(21)

(22)

式(17)表示该类型所有备件的保障度最大。

式(18)表示该类型所有备件保障费用最小。

约束(19)表示备件i在基层级的短缺率大于等于0,小于等于1。

约束(20)表示备件i在中继级的短缺率大于等于0,小于等于1。

约束(21)表示备件i在基层级的配置数量不超过最高库存限额,且为整数。

约束(22)表示备件i在中继级的配置数量不超过最高库存限额,且为整数。

2备件配置优化模型求解

2.1模型分析

由式(17)~式(22)可知,备件配置优化模型为高维、非线性优化模型,采用一般的优化算法难以奏效。为了进一步求解该类优化模型,本文对其做了以下分析与处理:

(1) 在本文构建的备件配置优化模型中,共有两个不同的目标函数,并且在不同时间阶段、不同任务需求中,决策者对这两个目标的偏好是不同的,因此,采用基于准则的方法求解MOPSO更为合理。

(2) 在粒子群算法中,ω是最重要的可控参数。针对粒子群算法容易早熟以及算法后期在全局最优解附近产生振荡的现象,需要对ω进行改进,以提高解的质量和求解的效率。

2.2粒子表示

本文采用基于向量的粒子表示方法,如图2所示。每个粒子对应一个备件配置方案,xn=[xn,1,…，xn,j,…,xn,m,xn,m+1],n∈{1,2,…,N},(N为粒子个数),粒子维数为m+1;xn,i表示备件在基层级的配置数量,j∈{1,2,…,m},m为基层级机构数量;xn,m+1表示备件在中继级的配置数量。

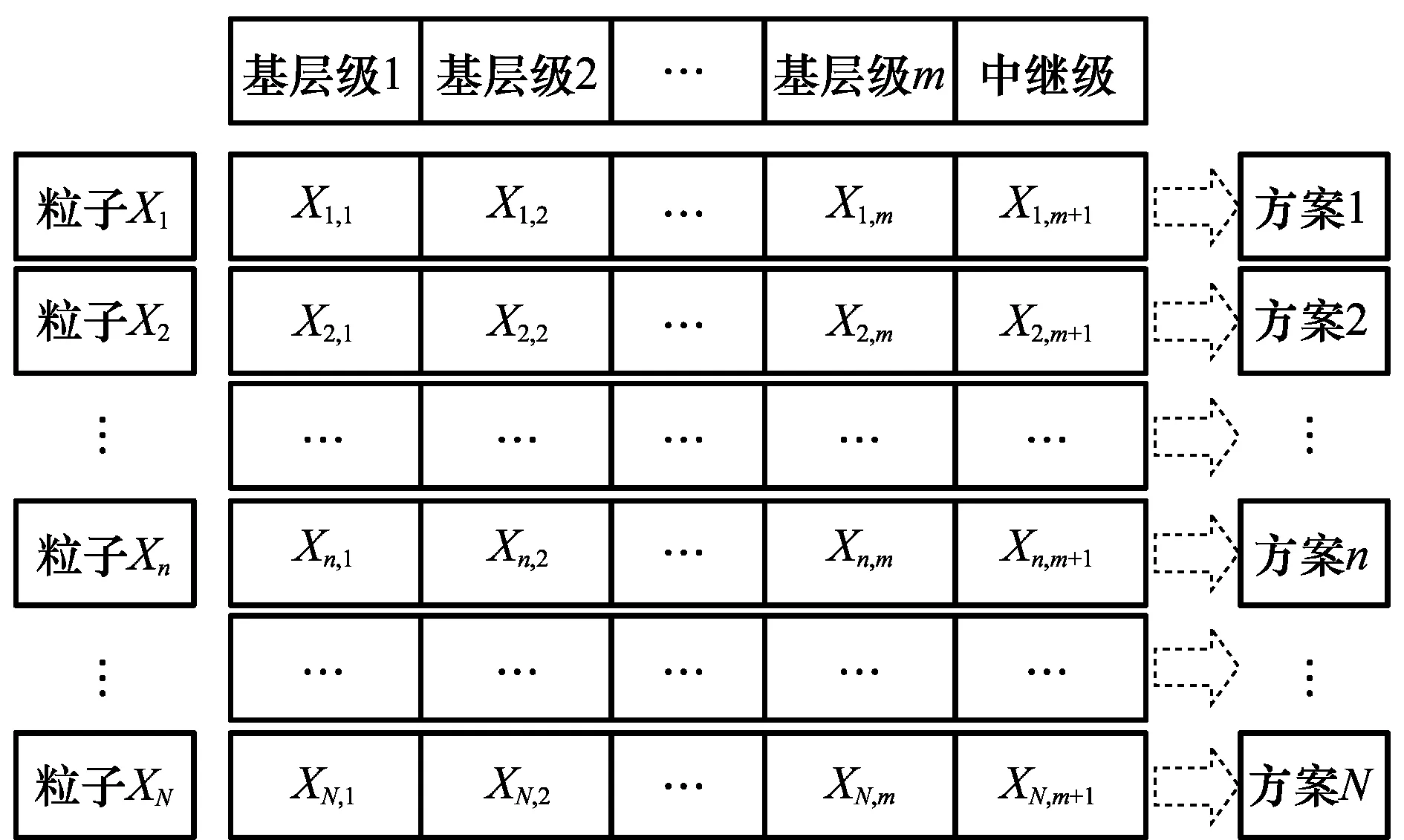
图2　粒子表示示意图

2.3适应度计算

适应度函数用来评价群体中个体的优劣,其数值引导着粒子群的移动方向与速度。针对备件i的保障度最大和保障费用最小两个目标,本文采用基于准则的方法来确定适应度函数,分别计算每个粒子的适应度,具体算法如下:

Pi=

(23)

(24)

2.4粒子更新

由于粒子群算法的快速收敛速度而极易导致种群多样性的损失,为了防止其陷入局部最优解,本文针对两个目标提出了选用两个粒子群的动态种群策略,设搜索空间为D维,总粒子数为n。每个粒子群优化一个单独的目标,第一个粒子群的全局最优粒子被用于第二个粒子群的速度方程中,而第二个粒子群的全局最优粒子又被用于第一个粒子群的速度更新中n,则

(25)

(26)

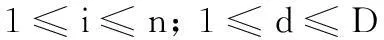
(27)

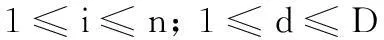
(28)

(29)

式中,c1和c2为常数,称为加速因子;r1,r2为[0,1]之间的随机数;ω称惯性因子;vi d(t) 表示在t时刻第i个粒子的速度;Sj,Vid(t) 表示在t时刻第j个粒子群第i个粒子的位置;Sj·pid(t)表示t时刻第j个粒子群“飞行”历史中的最优位置;Si·pgd(t) 表示t时刻第j个粒子群的全局最优粒子的位置。

2.5权重的改进

在粒子群算法中,惯性因子是最重要的可控参数,用来控制当前粒子速度更新后对粒子速度的影响程度。该参数越大,越有利于进行大范围全局搜索;该参数越小,越有利于在当前范围内进行局部搜索。通过大量试验表明[15],该参数在0.4~1.4间动态取值,效果较好。在本文中,惯性因子按以下公式选择:

(30)

式中,ωmax表示最大惯性权重；ωmin表示最小惯性权重；g表示迭代步数；Gmax表示最大迭代步数。

2.6算法流程

步骤 1初始化。随机初始化非劣解集(none-inferior solution set, NISS)和粒子群POP1、POP2,计算粒子群中每个粒子的目标以及约束,初始化粒子群中每个粒子的速度以及每个粒子所遍历到的最好点。

步骤 2更新粒子种群。按式(25)和式(26)更新粒子的速度,按式(27)~式(29)更新粒子的位置。

步骤 3更新非劣解集(NISS)。

步骤 4更新每个粒子所找到的最优解。

步骤 5终止条件判断,若满足则终止程序,否则转至步骤2。

MOPSO算法的基本流程如图3所示。

图3　基于准则的多目标粒子群算法流程

3算例分析

3.1问题描述

已知某师X、Y团均配备某型装备18台,A、B为该装备的两种关键备件,假设该装备只在团基层级修理机构修理,师中继级仅提供备件保障,t0为480 h,tm为720 h。单位时间内备件的需求概率Pji,平均故障间隔时间Tbf,以及故障率等参数见表1所示,为完成一年的训练任务(按1 600 h计算),如何配置该类备件,可使该系统备件的保障度最大,同时保障费用最小？

表1　初始数据

3.2问题求解与分析

计算可得备件在不同机构的需求数量Eji、Eoi等基础数据,详见表2所示。

表2　备件配置优化算例中基础数据

本文利用Matlab编写粒子群算法程序,在计算机配置为Intel(R) Core(TM)i5 CPU 2.27GHz 内存2G 时,两个种群规模均为40个粒子,迭代次数为100代,ωmax为1.2,ωmin为0.5,c1为0.5,c2为0.5时的平均计算时间为6 s。表3是备件在不同配置情况下的优化结果,图4为最优个体适应度的变化情况,图5是非劣解在目标空间的分布情况。从表3中可以看出,当保障费用为6 900元时,最优配置方案是备件A在中继级配置2件,备件B在中继级配置9件,此时备件的保障度为0.792;随着保障费用的增加,保障度也在不断增加。决策者可以根据需要和实际条件,从不同优化方案中选择合适的备件配置方案,以满足备件保障度和费用的要求。图4反映了最优个体适应度与进化代数关系,不难看出,当迭代到50代时最优个体的适应度基本趋于稳定值。

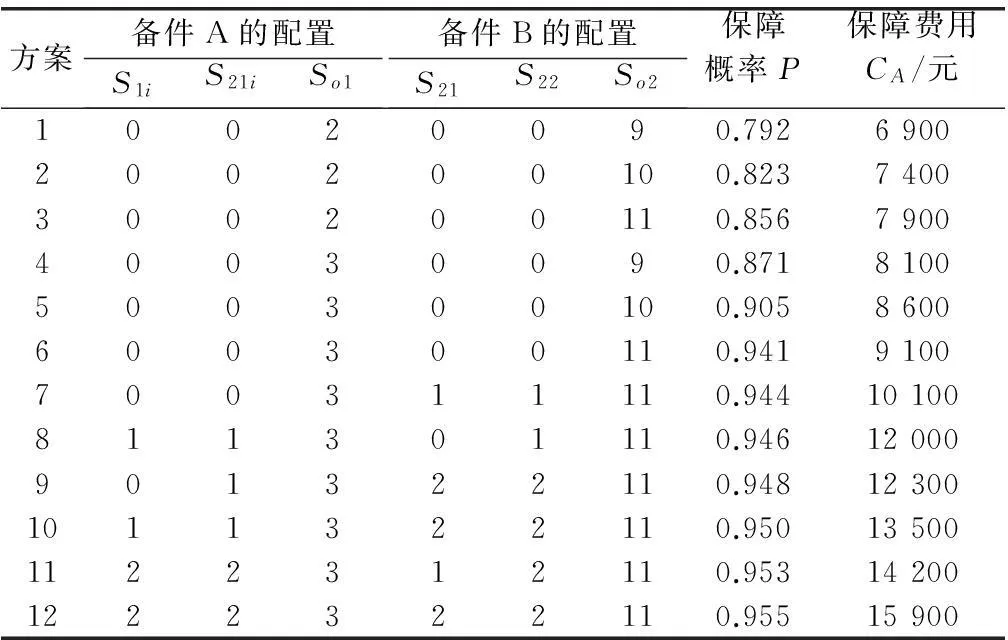
表3　备件配置优化结果

由图5可以看出,非劣解在目标空间的分布情况,即:在一定范围内随着保障费用的增加,备件保障度也在不断提高;当备件保障度达到0.95后,即使再增加保障费用,备件保障度的变化也是很小。另外,非劣解在目标空间的分布分别对应表3中的12个不同配置方案,决策者可以从保障费用和备件保障度两个目标进行综合权衡,从非劣解中选择确定一个合适的方案,进行备件的配置。

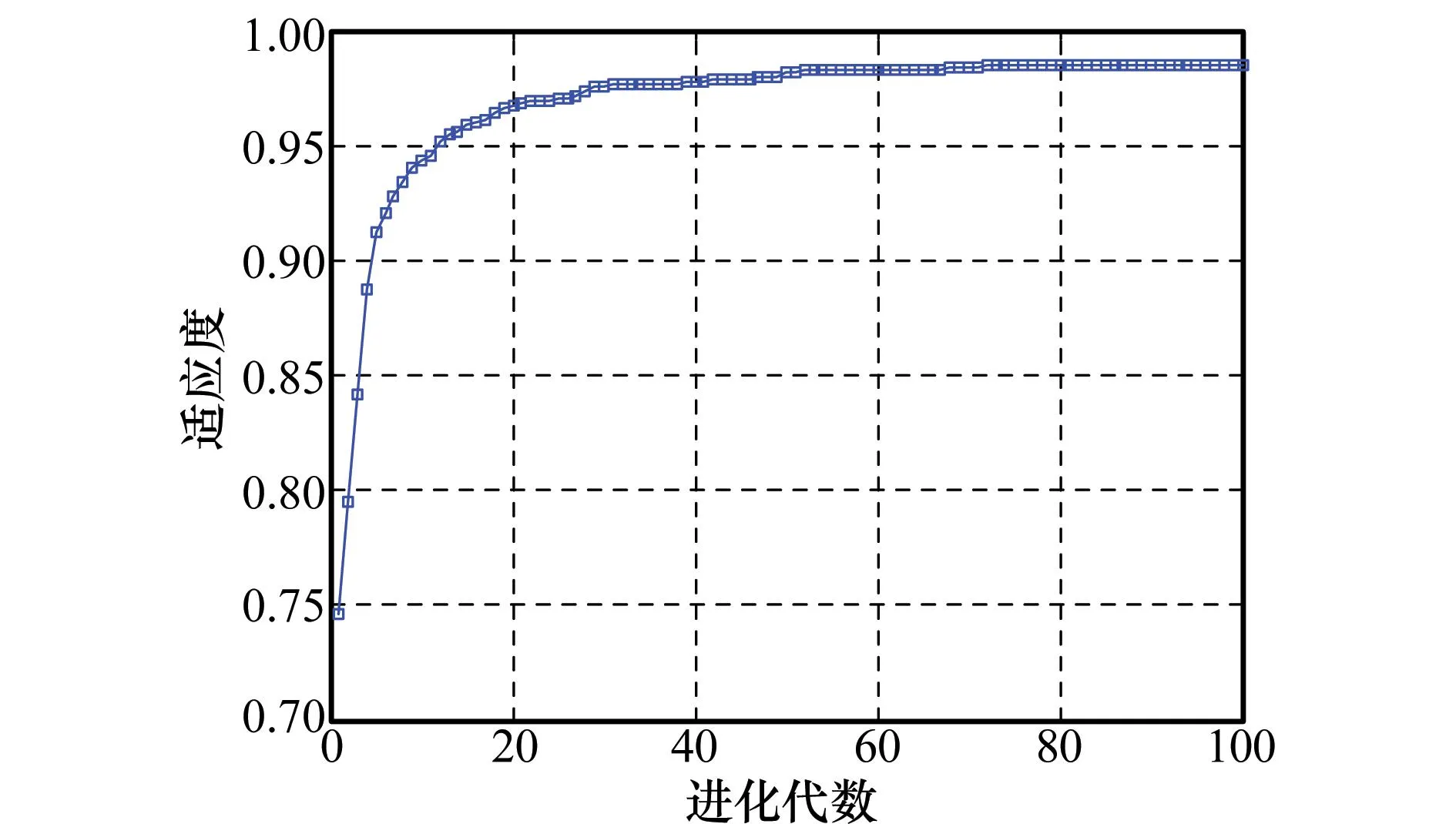
图4　备件MOPSO最优个体适应度的变化情况

图5　备件非劣解在目标空间的分布

例如,若要求备件的保障度不低于0.95,费用最小,则可以选择目标空间中的第10个非劣解(P=0.950,C=13 500元),此时的配置方案是备件A在两个基层级配置数量均为1件,在中继级配置数量为3件;备件B在两个基层级配置数量均为2件,在中继级配置数量为11件。

4结论

着眼多级维修保障系统的整体,同时考虑备件保障度、保障费用等目标,构建了备件的配置优化模型,引入了粒子群算法,两个目标作为引导,在备件配置方案生成时可以避免长时间的无效搜索,并通过算例验证了模型和算法的可行性与有效性,解决配置优化模型的高维、非线性求解难题,为备件的配置优化的科学决策提供了重要支撑。

参考文献：

[1] Wang W B. A joint spare part and maintenance inspection optimization model using the delay-time concept[J].ReliabilityEngineeringandSystemSafety, 2011, 96(4): 1535-1541.

[2] Ruan M Z, Li Q M, Li C. Improved layered marginal algorithm to optimize initial spare part configuration project[J].ActaArmamentarii,2012,33(10):1251-1257.(阮旻智,李庆民,李承.改进的分层边际算法优化备件的初始配置方案[J].兵工学报,2012,33(10):1251-1257.)

[3] Gao S, Yang J Y, Wu X J. Ant coling algorithm for optimization of system reliability[J].ComputerApplicationandSoftware, 2004, 21(12): 94-96.(高尚,杨静宇,吴小俊. 可靠性优化的蚁群算法[J].计算机应用与软件, 2004, 21(12): 94-96).

[4] Song G B, Ma G T, Liu X J, et al. Optimal allocation of initial spares of missile based on particle swarm optimization algorithm[J].ShipElectronicEngineering, 2012, 32(9): 118-120.(宋贵宝, 马广婷, 刘学君, 等. 基于粒子群算法的导弹初始备件优化配置[J].舰船电子工程, 2012, 32(9): 118-120.)

[5] Luo Y, Ruan M Z, Li Q M. Configuration project optimization for repairable spare parts under discretional structures[J].SystemsEngineeringandElectronics, 2012, 34(9): 1865-1871.(罗祎, 阮旻智, 李庆民. 任意结构下可修复备件的配置方案优化[J].系统工程与电子技术, 2012, 34(9):1865-1871.)

[6] Derek T D. Heuristic Algorithm for U.S. naval mission resource allocation[R]. ADA488672, 2008.

[7] Ilgin M A, Tunali S. Joint optimization of spare parts inventory and maintenance policies using genetic algorithms[J].InternationalJournalofAdvancedManufacturingTechnology, 2007, 30(5): 594-604.

[8] Guo Q, Zhang Z Y, Huang L P, et al. Research on optimization of disposition of spare parts for air defense weapon system based on METRIC theory[J].FireControl&CommandControl, 2011,36(8):100-103.(郭强,张振友,黄立坡,等.基于METRIC理论的防空武器系统备件配置优化[J].火力与指挥控制,2011,36(8):100-103.)

[9] Dong B C, Song B W, Liang Q W. The method of spares configuration optimization based on markov model[J].SystemsEngineering,2011,29(9):124-126.(董博超,宋保维,梁庆卫.马尔可夫模型的备件配置优化方法[J].系统工程,2011,29(9):124-126.)

[10] Ruan M Z, Peng Y W, Li Q M. Optimization of three-echelon inventory project for equipment spare parts based on system support degree[J].SystemsEngineering—Theory&Practice, 2012, 32(7): 1623-1630.(阮旻智, 彭英武, 李庆民. 基于体系保障度的装备备件三级库存方案优化[J].系统工程理论与实践, 2012, 32(7): 1623-1630.)

[11] Maripi J K. An effective parallel particle swarm optimization algorithm and its performance evaluation[D]. Carbondale: Southern Illinois University, 2010.

[12] Baltar A M, Fontane D G. Use of multi-objective particle swarm optimization in water resources management[J].JournalofWaterResourcesPlanningandManagement, 2008, 35(8): 257-265.

[13] Gong D W, Zhang Y, Zhang J H. Multi-objective particle swarm optimization based on minimal particle angle[J].LectureNotesinComputerScience, 2005, 3644(1): 571-576.

[14] Liang H B, Gao Q, Zhao J M, et al.Ordnancematerialmanagement[M].Beijing:Science Press,1998:122-129.(梁海滨,高崎,赵建民,等.军械维修器材管理学[M].北京:科学出版社,1998:122-129.)

[15] Liu H Y. Improvement of particle swarm optimization and its application in petroleum engineering[D]. Daqing: Northeast Petroleum University, 2012.(刘华蓥. 粒子群优化算法的改进研究及在石油工程中的应用[D]. 大庆: 东北石油大学, 2012.)

王亚彬(1975-),男,讲师,博士,主要研究方向为装备保障理论与应用。

E-mail:wangyabin123@163.com

赵建民(1961-),男,教授,博士,主要研究方向为装备保障理论与应用。

E-mail:jm_zhao@hotmail.com

程中华(1972-),男,副教授,博士,主要研究方向为装备保障理论与应用。

E-mail:cheng_zhonghua@163.com

王建增(1976-),男,工程师,主要研究方向为维修器材保障理论与应用。

E-mail:wang_jianzeng@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150104.1331.007.html

Optimization for spare parts allocation in multi-echelon

support system based on improved MOPSO

WANG Ya-bin1, ZHAO Jian-min1, CHENG Zhong-hua1, WANG Jian-zeng2

(1.DepartmentofEquipmentCommandandManagement,OrdnanceEngineeringCollege,

Shijiazhuang050003,China; 2.Unit66046ofthePLA,Shijiazhuang050000,China)

Abstract:Spare parts is a key component of equipment support, and a reasonable allocation plan of spare parts is the key factor for improving the efficacy of equipment support. Spare parts allocation and optimization in a multi-echelon support system presents difficult problems, which involves non-linear objective function and integer variables to be optimized. A multi-objective optimization model is developed, which maximizes support probability and minimizes support costs. In order to obtain the solution of the model, an improved multi-objective particle swarm optimization (MOPSO) method is employed, based on the traditional particle swarm method. The design idea and optimization procedure of this algorithm are put forward, rule based and inertia weigh improving method are introduced. In this method, dimensions reduction and rules-based multi-objective optimization are employed, which can improve the solving efficiency for the MOPSO method. At last, a numerical example is given, which examines the feasibility and validity of this method.

Keywords:multiple objective particle swarm optimization (MOPSO); spare parts; allocation; optimization; support probability

作者简介：

中图分类号：N 945.24

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2015.07.18

基金项目：“十二五”武器装备预研项目(51327020101)资助课题

收稿日期：2014-07-30；修回日期：2014-11-08；网络优先出版日期：2015-01-04。