基于改进PERT的装备使用保障过程建模分析

李廷鹏, 李　岳, 徐永成, 钱彦岭

(国防科学技术大学装备综合保障技术重点实验室, 湖南 长沙 410073)



基于改进PERT的装备使用保障过程建模分析

李廷鹏, 李岳, 徐永成, 钱彦岭

(国防科学技术大学装备综合保障技术重点实验室, 湖南 长沙 410073)

摘要：计划评审技术(program evaluation and review technique,PERT)自提出以来被广泛用于具有不确定时间参数项目的分析评估中,但经典PERT不能对具有随机后续工序的情况进行建模,而且存在时间参数估计主观性强,估计误差较大等不足。本文提出在经典PERT模型中加入跳转虚工序的方法增强其对随机工序的建模能力,并提出了相应的分析评估方法。另外,提出了基于德尔菲评估法与专家权重相结合并综合相似工序的历史数据的方法克服经典方法在时间参数确定方面的不足。最后,利用某装备的使用保障过程PERT建模分析实例验证了该方法的有效性。

关键词：计划评审技术; 德尔菲; 使用保障; 风险评估

0引言

计划评审技术(program evaluation and review technique, PERT)因其模型直观、原理简单、计算方便和可操作性较强的特点经常被运用到具有不确定时间参数项目的进度分析和风险评估中[1-2]。经典PERT能够对具有确定性逻辑关系的对象进行建模,但对于具有随机逻辑关系的对象却显得无能为力。为了增强PERT的建模能力,提出了跳转虚工序的概念,并在经典PERT分析方法的基础上提出了具有跳转虚工序PERT模型的分析方法。另外,经典PERT的时间参数通常是通过专家评估直接确定的,主观性强,误差较大,这也是导致估计值比实际值低的一个重要原因。为此,提出了基于德尔菲评估法与专家权重相结合并综合相似工序的历史数据的方法以克服经典方法在时间参数确定方面的不足。最后,详细介绍了某装备使用保障过程的PERT建模分析过程,验证了该方法的有效性。

1经典PERT

PERT是由美国学者Malcolm等在关键路径分析(critical path method, CPM)基础上于1958年提出的[3],自提出以来引起了大量学者的关注和研究[4-13]。经典PERT在解决实际问题中通常要经过以下3个步骤:① PERT建模;② 时间参数计算;③ 模型的求解。

PERT建模的实质是建立对象的网络图模型,网络图分为单代号网络图和双代号网络图[14]。在单代号网络图中,节点表示工序,箭头表示工序之间的逻辑关系。在双代号网络图中,节点表示工序的开始和或结束的状态,箭头代表工序。另外,在双代号网络图中,实线箭头表示常规工序(表示具体工作),虚线箭头表示虚工序(不代表具体工作,只刻画逻辑关系)。

1.1时间参数的计算

与CPM所不同的是,PERT的工序时间参数由乐观时间a,悲观时间b和最可能时间m组成,而且假设工序时间服从β分布,其概率密度函数为[15]

(1)

可以证明，PERT某项工作D(i,j)的时间均值和方差可以近似表示为[14]

(2)

(3)

1.1.1工作时间

PERT的工作时间包括最早可能开工时间TES(1,j),最早可能完工时间TEF(i,j),最迟可能开工时间TLS(i,j),最迟可能完工时间TLF(i,j):

(4)

(5)

上式表明,任意工作(i,j)的最早开工时间要由其所有紧前工作(k,i)的最早开工时间决定;其最早完工时间则等于其最早开工时间与工时之和。任一工作(i,j)的最迟开工时间要由其所有紧后工作(j,k)的最迟开工时间决定;其最迟完工时间则等于其最迟开工时间鱼工时之和。

1.1.2工作时差

工作时差包括总时差和自由时差。总时差是指在不影响任务总工期的条件下,某工作(i,j)的开工时间可以延迟的最大幅度,叫做该工作的总时差,记为TF(i,j),有

(6)

自由时差是指在不影响紧后工作最早开工时间条件下,其开工时间可以延迟的最大幅度,记为TF(i,j),则有

(7)

1.2模型的求解

1.2.1求解关键路径

在PERT网络的所有路线中,某一条路线持续时间长于其他路线持续时间的概率,大于其他路线持续时间长于该路线持续时间的概率,则该条路线称为关键路线[16],组成关键路径的工作称之为关键工作。关键路径的时间消耗即为整个模型的时间消耗,因此,通过分析关键路径可以对模型整体进行时间预测和风险评估。计算关键路径主要有3种方法[14]:①搜索从起点到终点的所有路径并计算时间消耗,最长者为关键路径;②计算各个工工序的总时差,时差为0的为关键工作,关键工作组成的路径即为关键路径;③计算从起点到终点的所有路径完成任务的概率,概率最小的为关键路径。

1.2.2风险分析评估

PERT的风险评估主要是评估不能按时完成任务的风险。由中心极限定理,当工序足够多,每项工序的工时对整个任务的总工时影响不大时,总工时近似服从正态分布。于是,给定工期TZ的按时完工概率为

(8)

式中,μ,σ为根据公式(2)计算得到的关键路径的均值和方差;Φ为标准正态分布的概率分布函数。

2改进PERT

经典PERT能够对具有确定性逻辑关系的对象具有很好的建模能力,但当某项工序的后续工序具有不确定性时,经典PERT就显得无能为力了。

例如，在某装备的使用保障过程中,需要对某部件进行检测,如果检测合格可直接使用,否则必须进行维修,维修完成后才能使用。此过程的经典PERT模型如图1所示。

图1某部件检测维修过程经典PERT模型

图中,A表示检测工序,B表示维修工序。分析此模型不难发现有以下几点不足:首先,从模型中不能直观反映出检测合格不需要维修的情况,因为从状态②(检测完成)到状态③(可以使用)只有唯一的一条路径(维修工序B);其次,即便是为了表示不维修的情况,将工序B的时间参数中最乐观值设定为0,由于需要同时考虑两种不同的情况,在工程实际中也很难估计出工序B的最悲观时间和最可能时间;再者,部件是否出现故障是一个随机过程,这就导致检测工序的后续工序(维修或者不维修)是不确定的且具有一定的发生概率,经典PERT也无法刻画这一特点。

因此,必须对经典PERT模型进行改进,以便能运用到对装备使用保障过程的分析中。

2.1改进PERT建模方法

为了增强经典PERT在具有不确定后续工序条件下的建模能力,本文建议在经典PERT模型基础上加入跳转虚工序。跳转虚工序跟虚工序一样不消耗时间和资源,是加在常规工序上的并行工序。跳转工序与对应的常规工序是互斥关系,每次只能执行其中一种。另外跳转虚工序和对应的常规工序都具有发生概率,且概率和为1。跳转虚工序的图形化表示为带箭头的弯曲虚线,在箭头的起点处标明跳转虚工序发生的概率。利用跳转虚工序对图1的PERT模型进行改进,结果如图2所示。

图2　某部件检测维修过程的改进PERT模型

图2中,A,B为常规工序,N为跳转虚工序。A表示检测,B表示维修。跳转虚工序N的发生概率为1-F%,工序B发生的概率为F%,F%是该部件的故障率。

对比图1、图2可以发现:改进的PERT模型不仅能直观的反应出检测工序的两种可能的后续工序(维修或者不维修),并且各个后续工序的时间参数能利用经典PERT方法直接得到。另外，后续工序发生的可能性也能通过发生概率直观表示。

2.2改进时间参数确定方法

时间参数是PERT分析评估的基础,参数的合理性和准确性对分析结果的可信度具有决定性作用。在工程实践中,PERT往往运用于工程方案的论证阶段,很难得到真实的统计数据。目前,时间参数基本上是通过专家评定确定的,传统的专家评定法完全依赖专家的经验知识,主观性太强,在一定程度上降低了评估结果的可信度。

为此,提出了基于德尔菲评估法与专家权重相结合并综合相似工序的历史数据的方法克服经典方法在时间参数确定方面的不足。该方法既考虑了专家的主观意见,也区分了不同专家对评估结果的不同贡献率,同时考虑客观的历史数据,使得评估的时间参数具有较高的可信度。

2.2.1德尔菲评估法

德尔菲评估法实质是多轮的专家评估法,但每次评估后会计算专家的评估值与该整体的平均加权值的偏差,并建议偏差较大的专家在下一轮评估的时候进行改变。通过n次反复后一般可以得到较为一致的评估值。具体步骤如下:①专家对每个参数给出评估值;②综合所有专家的评估值并计算得到平均加权值;③计算每个专家的评估值与平均值的偏差;④进行下一轮评估并建议偏差较大的专家对评估值进行调整;⑤重复步骤①~步骤④。德尔菲评估可以避免个别专家随意评估,保证评估数据的一致性。

2.2.2时间参数确定步骤

本文提出的时间参数确定法综合了专家的主观经验知识以及历史数据的客观规律,同时考虑了不同专家给出数据的可信度的差异。具体步骤如下:

步骤 1运用德尔菲方法得到每个工序的专家评估时间参数。每个工序的时间参数都包括乐观时间,悲观时间和最可能时间。

步骤 2根据专家的经验背景和预评估结果综合得到专家的权重。

预评估是指给出一个已知时间参数的工序和必要的其他参数让专家评估,比较专家评估值与真实值的差异。但预评估的结果会受到很多主客观因素的影响,不能完全反应出专家的评估能力。因此,预评估的结果只能作为确定专家权重的一个参考。需要充分分析专家的历史经验和背景知识,综合权衡出一组合理的权重系数。

步骤 3结合专家权重和专家评估原始数据通过加权得到评估参数:

(9)

式中,Tk是评估参数;Ti是第i各专家的评估值;qi是i个专家的权重系数,n为专家数,k代表每项工序的3个时间参数(乐观时间a、悲观时间b和最可能时间m)。

步骤 4收集相似工序真实的历史时间数据,并处理得到3个时间参数。本文提出按照如下原则从历史数据中计算时间参数:

(1) 最可能时间为所有历史时间的均值:

(10)

(2) 最乐观时间为历史数据中大于最可能时间Tm的所有数据均值:

(11)

(3) 最悲观时间为历史数据中小于最可能时间Tm的所有数据的均值:

(12)

步骤 5综合专家评估结果和历史数据得到最终的时间参数。

专家评估结果和历史数据计算的结果从不同方面为时间参数的确定提供了参考,参考价值的大小应该根据具体情况进行分析。例如,历史工序与待评估的工序相似度非常高且历史数据记录真实可信,那么历史数据的参考价值就更大些。可以利用权重区分各自的参考价值,然后利用加权的方法得到最终的估计值,如:

Tz=sjTj+slTl

(13)

式中，Tj为专家评估值；Tl为历史数据值；sj为专家评估值权重；sl为历史数据值权重,且sj+sl=1,sj>0，sl>0。

2.3改进分析评估方法

具有跳转虚工序的PERT模型不仅各个工序的时间是服从β分布随机变量,而且工序之间的逻辑关系也不再是确定的,而是满足一定概率的随机关系。因此,为了实现对具有跳转虚工序的PERT模型的求解必须研究新的分析方法。

前面提到过,求解关键路径有3种方法,由于改进模型本身具有的随机性的特点,只能采用第(2)、第(3)种方法求解。具有跳转虚工序的PERT模型关键路径的求解关键是如何处理跳转虚工序。为了能够利用传统方法求解,最好是能够将跳转虚工序按照一定的原则转化为常规工序。本文提出的具体方法如下:

将跳转虚工序的时间参数按如下公式转化为常规工序。

(14)

式中,Tt为跳转工序对应的常规工序原有的时间参数(包括最悲观时间,最可能时间和最乐观时间);f%为跳转虚工序发生概率。

这样将跳转虚工序和对应的常规工序转化为一个常规工序,再利用传统方法进行分析评估。

3实例分析

3.1建立PERT模型

某装备的使用保障过程由分解、分段测试、维修、组装、联调等多个主要工序构成。为了对该装备的使用保障任务能否按时完成进行风险评估,以及找出影响使用保障过程总时间的关键环节并给出优化建议,本文利用改进的PERT对该装备的使用保障过程进行了建模分析。首先建立了该装备使用保障过程的PERT模型,如图3所示。

图3　某装备使用保障过程PERT模型

该装备的使用保障过程PERT模型总共由15项常规工序、6个虚工序(G1,G2,G3,G4,G5,G6)和4个跳转虚工序(N1,N2,N3,N4)构成。各工序的意义及发生概率如表1所示。

表1　各工序的意义及发生概率

表1中,f1%,f2%,f3%,f4%分别为部件1、部件2、部件3、部件4的故障率。根据部件的可靠性试验结果以及对历史数据的统计分析得到部件的故障率如表2所示。

表2　各部件的故障率　%

3.2确定时间参数

为了较为准确地估计各个工序的时间参数,邀请3位专家以及6位装备保障使用保障过程的技术人员共同组成评估组对15项常规工序进行时间参数估计。

按照德尔菲原理,首先让评估人员根据自己的经验知识对各个工序进行时间参数的估计,经过4次交互评价,最终得到满足德尔菲原理的时间参数(本文设定每个评估人员的评估值与均值的误差不超过10%)。其中工序B(分解)的时间评估结果如表3所示,时间单位为min。

表3　工序B的专家评估时间参数详表　min

传统的时间参数确定方法是在专家评价的基础上进行均值化处理,没有考虑专家之间由于经验知识不同带来的差异。本文引入专家权重概念来体现专家对评估结果应具有的不同贡献率。

专家权重是通过对专家背景知识和历史经验的分析以及预评估情况综合分析计算得到的。专家权重如表4所示。

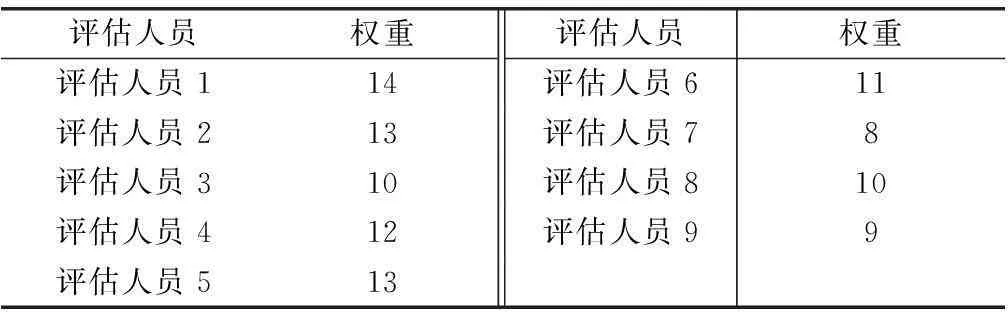
表4　各评估人员权重　%

按照加权评估的方式计算工序的时间参数,工序B通过专家评估法得到的时间参数如表5所示。

表5　工序B专家评估时间参数　min

相似工序的历史数据可以为时间参数的确定提供很有价值的参考,同时也能弥补专家评分主观性太强的不足。通过对相似装备使用保障过程的分析,找到了工序B类似的历史数据,对数据进行必要处理后得到可供参考的数据,如表6所示。

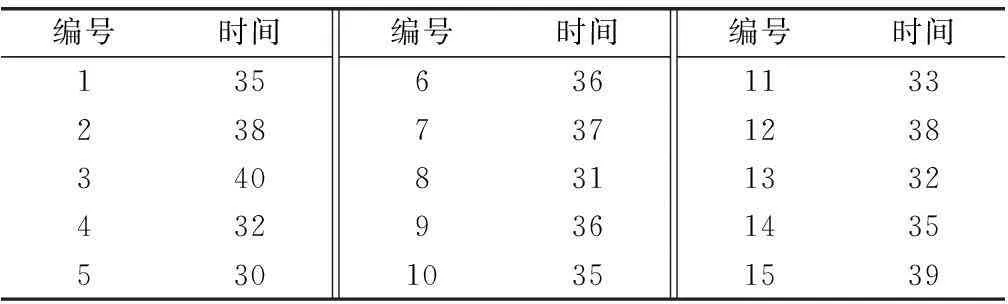
表6　工序B类似工序历史数据统计

利用式(10)~式(12)得到的历史数据时间参数如表7所示。

表7　工序B类似工序历史时间参数　min

综合专家数据和历史数据可以得到工序B的最终时间参数,权重和应根据历史数据的充分性以及参考意义确定,本文考虑到历史工序与B工序具有较高的相似度,确定sl=0.6,sj=0.4。计算结果如表8所示。

表8　工序B综合时间参数　min

按照以上步骤可以得到所有工序的时间参数,由于篇幅限制,这里不再详细说明。具体参数见表9所示。

表9　某装备使用保障过程各工序时间参数　min

3.3分析评估

为了分析装备使用保障过程中的关键工序,估计按时完成保障任务的概率,以及对现有保障方案提出优化建议,本文在建立使用保障过程PERT模型的基础上进行了关键路径分析和风险评估。

3.3.1关键路径分析

分析带有跳转虚工序的PERT模型首先应该对跳转虚工序进行转化。如图3的模型中有4个跳转虚工序,按照式(14)转化,结果如表10所示。

表10　跳转虚工序转化结果　min

本文通过计算各个工作的自由时间来确定关键路径,按照式(2)、式(4)、式(5)通过Matlab编程计算得到各工序的自由时间,如表11所示。

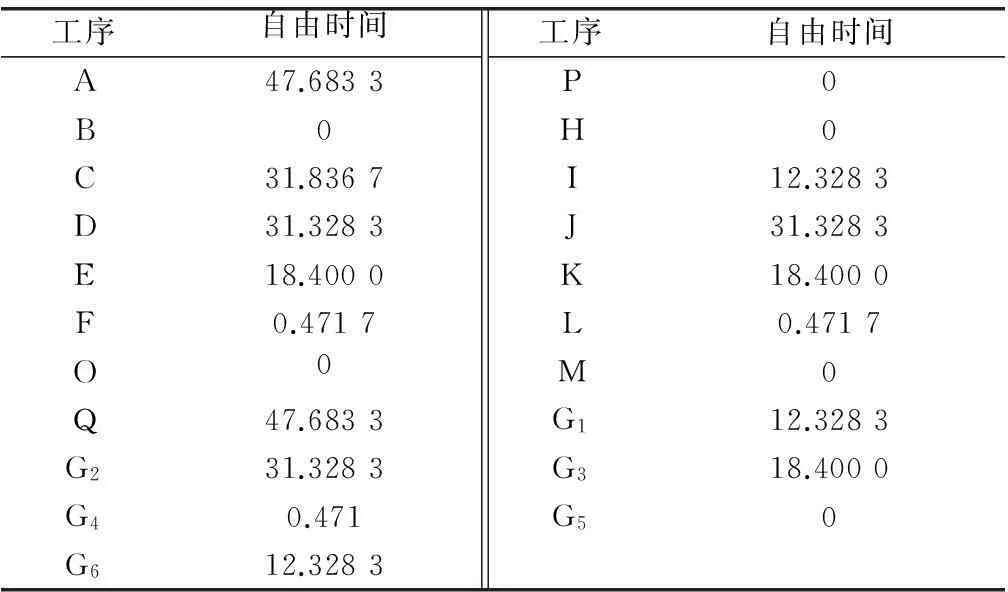
表11　各工序自由时间　min

由表11可得到自由时间为0的工序共有6个,因此关键路径为:B→H→M→G5→O→P。

3.3.2风险评估

风险评估实质是计算在目标时间之前完成所有工序的概率,关键路径是整个模型耗时最长的路径,因此,整个模型的风险评估就转化为计算关键路径在目前时间前完成的概率。关键路径均值和方差如表12所示。

表12　关键工序的均值和方差

由公式(2)得到关键路径的均值和方差分别为μ=127.37,σ=4.77。

装备的使用保障要求保障过程须在130 min内完成,由公式(8)计算得到完成的概率为70.8%,概率较低。因此必须对关键路径上的工序进行压缩,才能避免较大不能按时完成任务的风险。

4结论

本文针对经典PERT在时间参数确定上的不足,提出了基于德尔菲评估法与专家权重相结合并综合相似工序的历史数据的方法确定时间参数。该方法不但考虑了专家的主观经验知识,体现了不同专家对估计结果的不同贡献率,而且充分利用了相似的历史数据的客观信息。另外,考虑到经典PERT模型在表示具有随机后续工序时存在困难,本文提出跳转虚工序的概念,同时给出了分析具有虚工序PERT模型的方法。最后,某装备的使用保障过程的PERT建模分析验证了所提理论方法的合理性和实用性。

参考文献：

[1] Castro J, Gómez D, Tejada J.Allocating slacks in stochastic PERT network[J].CentralEuropeanJournalofOperationsResearch, 2014, 22(3): 37-52.

[2] Wang Z F, Ding J Y, Liu Y, et al. Analysis of critical path and most critical activity in PERT networks based on Monte Carlo method[J].SystemsEngineeringandElectronics, 2012, 34(8): 1646-1671.(王卓甫, 丁继勇, 刘媛, 等. 基于蒙特卡罗方法的PERT网络关键路线和最关键活动分析[J].系统工程与电子技术, 2012, 34(8): 1646-1671.)

[3] Li Y, Yu H S, Shen Q,et al. An estimating method for aviation project’s duration based on improved-PERT[J].IndustrialEngineeringandManagement,2007(4):38-42.(李阳,于海山,沈琴,等.改进的PERT项目工期估算方法[J].工业工程与管理,2007(4):38-42.)

[4] Konstantinos A C, Basil K P. Approaching activity duration in PERT by means of fuzzy sets theory and statistics[J].JournalofIntelligent&FuzzySystems, 2014, 26(2): 577-587.

[5] Keefer D L, Verdini W A. Better estimation of PERT activity times[J].ManagementScience, 1993, 39(9): 1086-1091.

[6] Hahn E D. Mixture densities for project management activity times: a robust approach to PERT[J].EuropeanJournalofOperationalResearch, 2008, 188(2): 450-459.

[7] Sasieni M. A note on PERT times[J].ManagementScience, 1986, 32(12): 1652-1653.

[8] Herrer1′as-Velasco J M, Herrer1′as-Pleguezuelo R, Van Dorp J R. Revisiting the PERT mean and variance[J].EuropeanJournalofOperationalResearch, 2011, 210(2): 448-451.

[9] Miklos H, Orsolya B. The effects of different activity distributions on project duration in PERT networks[J].Procedia-SocialandBehavioralSciences, 2014, 119: 766-775.

[10] Mouhoub N E, Benhocine A, Belouadah H. A new method for constructing a minimal PERT network[J].AppliedMathematicalModelling, 2011, 35(9): 4575-4588.

[11] Hashemin S S, Fatemi Ghomi S M T, Modarres M. Optimal constrained non-renewable resource allocation in PERT networks with discrete activity times[J].SharifUniversityofTechnology, 2012, 19(3): 841-848.

[12] Yaghoubi S, Noori S, Azaron A, et al. Resource allocation in dynamic PERT networks with finite capacity[J].EuropeanJournalofOperationalResearch, 2011, 215(3): 670-678.

[13] Xiong X D, Wang R Y, Zhang L Z, et al. The improvement of PERT based on particle swarm optimization arithmetic[J].ComputerApplication,2012,32(6):1734-1737.(熊选东,汪若洋,张亮忠,等.基于微粒群优化算法的计划评审技术改进[J].计算机应用,2012,32(6):1734-1737.)

[14] Zuo C Y. Optimization analysis of missiles’technical preparation process based on PERT[J].JournalofNavalAeronauticalandAstronauticalUniversity,2008,23(5):569-572.(左传友.PERT方法优化的导弹技术准备流程[J].海军航空工程学院学报,2008,23(5): 569-572.)

[15] Guo X W, Ma D W, Deng L. Optimal allocation of air ammunition support crew based on PERT networks[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2014, 40(1): 69-74.(郭小威, 马登武, 邓力. 基于PERT网络的航空弹药保障人员优化配置[J].北京航空航天大学学报, 2014, 40(1): 69-74.)

[16] Soroush H M.The most critical path in a PERT network: aheuristic approach[J].EurpopeanJournalofOperationalResearch, 1994, 78(1): 93-105.

李廷鹏(1987-),男,博士研究生,主要研究方向为装备综合保障。

E-mail:tovey1987@126.com

李岳(1964-),男,教授,博士研究生导师,主要研究方向为装备综合保障。

E-mail:liyue@nudt.edu.cn

徐永成(1971-),男,教授,博士,主要研究方向为装备综合保障。

E-mail:ycxu@nudt.edu.cn

钱彦岭(1976-)男,副教授,博士,主要研究方向为装备综合保障。

E-mail:ylqian@nudt.edu.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141030.1136.014.html

Modeling and analysis of operation support progress of

equipment based on improved PERT

LI Ting-peng, LI Yue, XU Yong-cheng, QIAN Yan-ling

(ScienceandTechnologyonIntegratedLogisticsSupportLaboratory,NationalUniversityof

DefenseTechnology,Changsha410073,China)

Abstract:The program evaluation and review technique (PERT) is widely taken into analysis and evaluation of programs which include random time parameters, but the classical PERT is limited in modeling the case including random after working procedure and the method of time parameters evaluation is subjectivity and inaccurate. A jump virtual working procedure concept and its analysis method are proposed to enhance the modeling ability of the classical PERT. Moreover, a new time parameters evaluation theory is presented to improve the reliability of parameters, which combines the Delphi evaluation method with experts’ weight and takes the similar history data into account. Finally, a detaild analysis and evaluation of the operation support process of equipment based on the improved PERT validates the practicability of the proposed method.

Keywords:program evaluation and review technique (PERT); Delphi; operation support; risk evaluation

作者简介：

中图分类号：C 931; TH 17

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2015.07.17

收稿日期：2014-05-15；修回日期：2014-07-29；网络优先出版日期：2014-10-30。