卫星与浮空器协同侦察任务规划方法

胡笑旋， 朱外明， 马华伟

(1. 合肥工业大学管理学院， 安徽 合肥 230009；

2. 合肥工业大学飞行器网络系统研究所， 安徽 合肥 230009)



卫星与浮空器协同侦察任务规划方法

胡笑旋1,2， 朱外明1,2， 马华伟1,2

(1. 合肥工业大学管理学院， 安徽 合肥 230009；

2. 合肥工业大学飞行器网络系统研究所， 安徽 合肥 230009)

摘要：针对卫星和浮空器协同对地侦察任务规划问题，提出了一种分阶段任务规划方法，将卫星与浮空器协同任务规划分为任务聚类、任务组分配和任务排程3个相继的阶段。使用层次聚类算法进行任务聚类，通过聚类形成多个任务组；给出了任务组分配的规划模型，将任务组与平台资源进行匹配；建立了任务排程的混合整数规划模型，并使用粒子群算法进行求解，将任务最终分配到相应的平台上。仿真结果表明，所提出的方法可行且有效。

关键词：卫星; 浮空平台; 协同侦察; 聚类; 任务规划

0引言

成像侦察卫星能够利用星载遥感设备，从空间轨道对指定的可覆盖的目标实施侦察。由于卫星资源的有限性、载荷的多样性和侦察任务的不确定性等因素，使得卫星任务规划成为重要的研究领域。近年来，国内外学者针对单星任务规划、多星协同规划等方面进行了研究。对于单星任务规划，整数规划和图论是经典的处理方法。文献[1]介绍了成像卫星任务规划的0-1整数规划模型，使用二进制变量表示传感器对目标的选择与否，将侦察目标间的时间互斥性转化为约束。文献[2]采用图论的方法，将侦察目标看作节点，沿卫星前进方向连接无时间互斥的节点，组成时间序、有向、无圈连通图，卫星侦察目标的选择为连通图中总权重最大的一条路径。对于多星任务规划，文献[3]采用预先分配的方式先将任务分配到各单卫星，然后各单星分别进行任务规划。文献[4]使用0-1型整数变量表示任务对卫星的选择，使用连续型变量表示时间，建立起LTAP问题的混合整数线性规划模型。其他还有合同网协议[5]、多维背包[6]等模型。卫星任务规划的求解算法多样，有遗传算法[7]、禁忌搜索[8]、粒子群算法[9]等。

临近空间浮空器具有与卫星所不同的特点[10-11]，它能够在指定的空域中定点悬停，具有驻留时间长，效费比高等优点。随着通信技术的发展，平台间的通信链路日益完善，卫星与浮空器协同侦察已逐渐走向应用。将卫星和浮空器组成协同系统，共同完成对地侦察任务，能够实现不同类型平台能力互补，扩大同一时刻覆盖范围，缩短目标重访时间，降低总体侦察成本等。

卫星与浮空器协同侦察对任务规划技术提出了更高的要求，其问题的复杂性主要体现在如下几点：①平台的运动方式不同，卫星平台在空间轨道中高速运动，而浮空器在空域中定点悬停，如何基于不同的运行方式建立统一的规划模型是一个难点；②任务有时间要求，需要在规定的时间内完成，任务对平台的选择要顾及其时间特性；③任务之间存在复杂的耦合关系，耦合关系的存在增加了规划问题的复杂度。

本文研究了一种卫星与浮空器协同侦察任务规划方法，将整个任务规划过程分解为任务聚类、任务组分配和任务排程3个相继的阶段，使用层次聚类算法进行任务聚类，给出了任务组分配模型和任务排程模型，使用粒子群算法进行求解，最后基于Matlab和卫星工具箱(satellite tool kit, STK)进行了仿真实验。

1问题描述

本文所研究的任务规划问题可概括为：在满足侦察任务需求约束(主要包括任务传感器类型约束、任务时间约束、任务耦合关系约束等)和卫星、浮空器资源约束的条件下，以最大化任务收益为目标，制定目标集合T在资源集合R上的计划安排，即为每一个平台指定任务和任务的执行时间。本文假设如下：①一个平台只搭载一个侦察传感器；②具有耦合关系的任务具有一致的传感器类型要求，且处于同一时段内；③浮空器按照一定的顺序对其所能覆盖的目标进行侦察。

2任务规划流程设计

协同侦察的平台资源具有不同的时空行为，侦察卫星是高速移动的天基平台，具有严格的轨道限制，而浮空器没有高速移动的特点，是一种定点平台。因此，卫星和浮空器协同侦察任务规划的过程较为复杂，要考虑不同平台在对地覆盖的范围和时间窗上的差异。本文将任务规划过程分解成3个相继的阶段，分别为任务聚类、任务组分配和任务排程，如图1所示。通过这3个阶段的依次执行，完成卫星和浮空器的协同侦察任务规划。

图1　任务规划流程

其中任务聚类是将用户提交的任务基于时间、地理位置、传感器需求等属性进行聚合，形成不同的任务组的过程。属于同一个任务组中的任务可以由相似的平台执行。任务组分配是将平台某一时段的工作时间划分给某一任务组的过程，实现任务组到平台的预分配。任务排程是对各任务组内的任务进行详细规划，确定每个任务执行的平台和时间。

3任务聚类

通过任务聚类形成任务组，任务组是一个任务子集，组内的任务具有相同或相近的特性。任务聚类时要综合考虑任务所要求的传感器类型、任务区域、任务时间等多个属性。层次聚类算法[11-12]具有简单、快速的特点，有自顶向下和自底向上2种策略。本文选取层次聚类算法实现聚类，采用自底向上的策略，首先将每个任务各自作为一个任务组，然后逐步的合并成为越来越大的任务组，直到全部都聚成一个任务组或某个终止条件得到满足。

3.1时间距离计算

(1)

3.2空间距离计算

步骤 1将经纬度转换成空间坐标。如图2所示，设ti对应点A，tj对应点B。α为A的纬度，β为A的经度，R为地球半径，则A点的三维坐标由式(2)计算获得:

(2)

图2　经纬度与直角坐标转换示意图

步骤 2计算两点之间的空间直线距离D,直接由空间距离公式(3)计算获得:

(3)

步骤 3根据立体几何计算出其球面距离。如图2所示，A、B两点的直线距离D已由步骤2计算得到，根据立体几何，A,B之间的球面距离由式(4)计算得到:

(4)

3.3传感器类型距离计算

(5)

式中，M为给定的足够大的整数。

3.4任务合成距离计算

任务ti与tj之间的距离dij是综合时间距离、空间距离、传感器类型距离得到，其计算公式如式(6)所示(其中，L为给定的参数)。

(6)

式(6)表明，当任务ti与tj的时间距离超过一定数值L时，或ti与tj所要求传感器的类型不一致时，将ti与tj之间的距离dij计为M，以使2个任务聚到不同的任务组中。其他情况下，dij定义为ti与tj的空间距离。

令G= {gl|l= 1, 2, …,NG}表示聚成的任务组，其中NG表示任务组的数量。令Dlm(l,m=1, 2,…,NG)表示任务组之间的距离，其计算公式为

(7)

Dlm的更新采用最小距离方法，即新聚成的任务组与其他任务组之间的距离使用该任务组中的任务与其他任务组中的任务之间的最小距离代替。

输入：任务集合T，聚成的任务组数NG。

输出：任务组G= {gl|l= 1, 2, …,NG}。

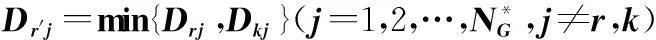
4任务组分配

(8)

(10)

5任务排程

通过任务聚类将大量广布的任务划分成NG个任务组，又通过任务组分配建立了任务组与资源之间的分配关系，使得特定的任务组合可以交由特定平台的特定时段去执行。任务排程是在各平台组合内进行任务执行详细计划的制定，即确定具体的任务由哪个平台在何时执行。

5.1数学模型

(11)

5.2求解算法

任务排程的数学模型为混合整数规划模型，当任务增多时，选择组合成指数增长，适合采用智能求解算法进行求解。粒子群算法具有易实现、精度高、收敛快等优点，在求解组合优化问题表现出较大优势。

粒子群算法是从鸟类捕食的行为中得到启发而产生，文献[13-14]提出，属于进化算法的一种。粒子群算法通过更新各个粒子的位置、飞行的速度和适应度，使得搜索不断地向前迭代，最终寻找到优良的解，其速度和位置更新公式分别见式(21)和式(22)。

(21)

(22)

5.2.1编码方式

职业教育是我国教育领域的主要构成部分，对推动经济增长有着十分重要的作用。学校基层行政工作者是管理教育的主要构成部分，在培育人才的过程中承担着十分关键的责任。不过，在职业教育发展中，高校始终倾向于教师文化素养与教育能力的提升，普遍忽略了行政工作者的职业特征与心理活动，进而导致学校的行政管理者出现普遍性的职业倦怠现象。

使用整数编码方式对二进制决策变量进行编码。任务对资源的选择具有唯一性，即一个任务最多选择一个资源。因此任务的选择有2种情况：一是任务得以执行，并选择一个平台资源执行；二是得不到执行，不选择任何平台资源。采用以下编码方式确定任务对资源的选择：

(1) 使用整数对资源进行编号，增加虚拟资源编号0；

(2) 使用一维整数变量表示任务选择的资源编号，当变量选择资源0时表示任务不执行。

例如一维变量X取值如表1所示。

表1　一维变量X取值

表1说明，任务1、2、3、5分别由资源1、3、3、2执行，任务4不执行。

5.2.2更新方式

(1) 惯性权重。惯性权重w衡量粒子对以前的学习状况，在标准粒子群算法后期的迭代过程中，种群容易陷入局部最优。为使算法的运行更加稳健，设置惯性权重w的值随着迭代次数的增加而线性递减。

(2) 收缩因子。收缩因子是文献[15]提出的对标准粒子群算法的一种改进，旨在促进算法的收敛。改进后的速度更新公式见式(23)。

(23)

式中，χ为收缩因子，其计算公式为

6仿真实验

根据本文所介绍的相关技术，进行了任务聚类、任务组分配和任务排程的仿真实验。实验平台：CPU为Intel Core i5 3.10 GHz，内存为4 GB。实验基于Matlab编程实现，其中平台资源对目标覆盖的时间窗采用STK 9.0软件计算。

6.1任务聚类与任务组分配实验

6.1.1方法可行性验证

按照均匀分布的原则，选取不同时段、不同经纬度、不同传感器要求的侦察任务共100个，如图3所示。选取4颗卫星平台和3个定点浮空器平台进行实验，其中卫星的时段使用其轨道圈次计算，即卫星一个轨道圈次计为卫星的一个可用时段。浮空器为部署好的定点平台,各平台数据如表2所示。

图3　任务目标分布图

资源类型传感器类型可用时段个数r1卫星114r2卫星115r3卫星214r4卫星214r5浮空器210r6浮空器110r7浮空器110

实验中的传感器类型有2类,任务的时间要求从某日的0点到24点之间。首先进行任务聚类实验，根据任务的传感器类型要求、区域位置、时段的不同，要求聚为8类。然后使用表1中平台数据，结合任务聚类的结果进行任务组分配实验，使用STK计算出平台对任务的覆盖数据，并据此计算各平台时段资源分配给各任务组的收益，使用Matlab线性规划工具箱求解。任务聚类与任务组分配的实验结果见表3。

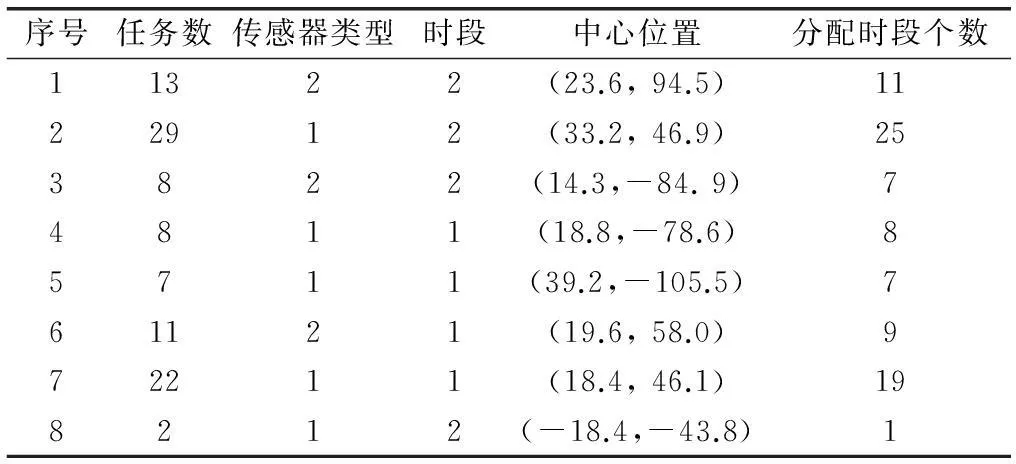
表3　任务聚类与任务组分配的实验结果

分析实验结果，各任务组内的任务均具有传感器类型要求相同、时段相同、区域位置集中的特点。各任务组之间具有明显不同的任务特性。从任务组的分配结果可以看出，当任务组内包含的任务数较多时，对应分配的时段个数也就越多，这是因为在较多任务的任务组内，资源覆盖的任务数较多，则平台时段资源分配给该任务组的收益越大，导致资源越向该任务组集中。但由于时段、传感器类型等限制，没有产生过度集中的现象。

6.1.2方法效率分析

为了分析算法和模型的效率，分别使用不同数量的任务进行任务聚类和任务组分配实验，表4记录了任务数在100~1 000的实验的耗时数据。

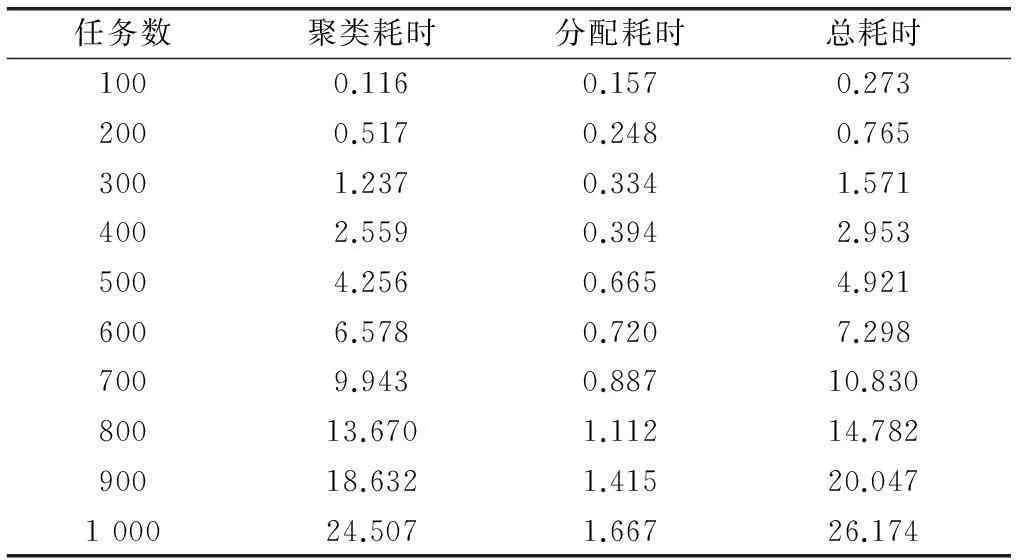
表4　任务聚类和任务组分配实验效率统计　s

由表4可知，随着任务数的增多，任务聚类和任务组分配的耗时在不断增加。但对应任务数的增加，耗时的增长呈现近似线性形式，在规划过程中是可以接受的。

6.2任务排程实验

为验证任务排程的混合整数规划模型，选取一定数量的任务，目标分布见图4，使用表1中的平台进行实验(此时假设平台具有相同特性的传感器)。卫星侦察时间窗采用STK计算，浮空器按照一定的顺序对其所能覆盖的目标进行侦察。规划周期从某日的0点到12点，各平台资源在各时段内对各目标无重访现象。同时，在任务周期内随机设置任务的时间要求，随机给定任务的优先级，实验所用其他数据使用计算机随机生成。基于Matlab采用粒子群算法进行求解。

图4　任务排程的目标分布

6.2.1任务排程的协同程度分析

在满约束下使用不同任务数进行实验，分别记录浮空器执行任务数、卫星平台执行任务数，分析浮空器和卫星平台协同执行任务的情况，相关的数据见表5。由表5可知，随着任务数目的增多，执行的总任务数在逐渐减少。算例不同，所获取数据存在差异，但浮空器执行的任务占总执行任务的比重相对稳定，未出现过度偏离的现象。协同效果的好坏与任务的耦合关系的设置不无影响。

表5　卫星与浮空器协同程度分析

6.2.2任务排程的效率分析

在不同任务数下，随机的设置捆绑关系和紧前关系，分别进行无捆绑且无紧前约束、只附带捆绑约束、只附带紧前约束和满约束实验，分别记录每种情况下的时耗和规划成功任务占总任务的比重，见图5和图6。由图5可知，在没有捆绑或紧前约束的情况下，任务规划求解的效率较高。但是，提供高质量的信息服务，任务之间的耦合关系必须考虑。随着任务数目的增多，描述任务耦合关系的矩阵也越来越大，进行处理所要消耗的时间也越来越大。由图6可知，在资源相对充足的条件下，任务的耦合关系约束成为影响任务完成率的主要因素。任务的耦合关系越多，平台就越难以按照要求执行可选的任务，使得耦合的任务均得不到执行。但任务的耦合关系必须考虑，此时可以通过增加资源种类，利用各种平台协同而作，提升任务的完成率。在其他条件不变的情况下，使用不同数量的平台进行实验，资源越充足，总体任务的完成程度越大，但规划消耗的时间也相应地增大。

图5　不同约束下规划的效率分析

图6　不同约束下规划成功任务占总任务的比重

7结论

任务规划是成像侦察卫星与浮空器应用中的关键技术之一。本文以成像侦察卫星和浮空器为对象，分析了卫星与浮空器协同侦察的优势，结合实际需求，设计了一种分阶段的卫星与浮空器协同侦察任务规划方法，将整个规划过程分解为任务聚类、任务组分配和任务排程3个相继的阶段。通过分解，降低了任务规划问题的求解难度。随后，使用层次聚类算法进行任务聚类，给出了任务组分配和任务排程的数学规划模型，并使用粒子群优化算法进行求解。根据所提出的模型和算法，基于STK和Matlab进行了仿真实验。实验结果验证了所提出的方法的可行性和有效性。

参考文献：

[1] Gabrel V. Strengthened 0-1 linear formulation for the daily satellite mission planning[J].JournalofCombinatorialOptimization, 2006, 11(3): 341-346.

[2] Chen H, Li J, Jing N, et al. Scheduling model and algorithms for autonomous electromagnetic detection satellites[J].ActaAeronauticaetAstronauticaSinica, 2010, 31(5): 1045-1053. (陈浩, 李军, 景宁, 等. 电磁探测卫星星上自主规划模型及优化算法[J]. 航空学报, 2010, 31(5): 1045-1053.)

[3] Wang Z Y, Wang Y Q, Wang J, et al. New multi-satellite scheduling method[J].ChineseSpaceScienceandTechnology, 2012(1): 8-14. (王智勇, 王永强, 王钧, 等. 多星联合任务规划方法[J]. 中国空间科学技术, 2012(1): 8-14.)

[4] Wang H B, Xu M Q, Wang R X, et al. Long-term acquisition plan method for small satellites constellation[J].SystemsEngineeringandElectronics, 2011, 33(6): 1293-1298. (王海波, 徐敏强, 王日新, 等. 对地观测小卫星星座长期任务规划求解技术[J]. 系统工程与电子技术, 2011, 33(6): 1293-1298.)

[5] Gao L, Zhou L A, Sha J C. Task allocation model and algorithm for DSS cooperation mechanism[J].JournalofSystemsEngineering, 2009, 24(4): 445-450. (高黎, 周利安, 沙基昌. 分布式卫星系统协作任务分配模型及优化算法[J]. 系统工程学报, 2009, 24(4): 445-450.)

[6] Vasquez M, Hao J K. A “logic-constrained” knapsack formulation and a tabu algorithm for the daily photograph scheduling of an earth observation satellite[J].ComputationalOptimizationandApplications, 2001, 20(2): 137-157.

[7] Mansour M A A, Dessouky M M. A genetic algorithm approach for solving the daily photograph selection problem of the SPOT5 satellite[J].Computers&IndustrialEngineering, 2010, 58(3): 509-520.

[8] Bianchessi N, Cordeau J F, Desrosiers J, et al. A heuristic for the multi-satellite, multi-orbit and multi-user management of earth observation satellites[J].EuropeanJournalofOperationalResearch, 2007, 177(2): 750-762.

[9] Yin P Y, Yu S S, Wang P P, et al. A hybrid particle swarm optimization algorithm for optimal task assignment in distributed systems[J].ComputerStandards&Interfaces, 2006, 28(4): 441-450.

[10] Jing X L, Zhang J W, Huang S C. Development actuality and key technology of near space[J].AerospaceManufacturingTechnology, 2011(2): 17-21. (景晓龙, 张建伟, 黄树彩. 临近空间发展现状与关键技术研究[J]. 航天制造技术, 2011(2): 17-21.)

[11] Jain A K, Murty M N, Flynn P J. Data clustering: a review[J].ACMComputingSurveys, 1999, 31(3): 264-323.

[12] Murtagh F. A survey of recent advances in hierarchical clustering algorithms[J].TheComputerJournal,1983,26(4):354-359.

[13] Kennedy J, Eberhart R. Particle swarm optimization[C]∥Proc.oftheIEEEInternationalConferenceonNeuralNetworks, 1995, 4(2): 1942-1948.

[14] Parsopoulos K E, Vrahatis M N.Particleswarmoptimizationandintelligence:advancesandapplications[M]. Hershey: Information Science Reference, 2010.

[15] Clerc M, Kennedy J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J].IEEETrans.onEvolutionaryComputation, 2002, 6(1):58-73.

胡笑旋(1978-)，男，教授，博士，主要研究方向为空间信息网络任务规划与资源调度。

E-mail：xiaoxuanhu@hfut.edu.cn

朱外明(1988-)，男，硕士研究生，主要研究方向为空间信息网络任务规划与资源调度。

E-mail：zhuwaiming@hfutfxqs.com

马华伟(1977-)，男，副教授，博士，主要研究方向为物流与供应链管理、管理信息系统。

E-mail：colt_mhw@126.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141019.2345.008.html

Method of satellite and aerostat cooperative reconnaissance

mission planning

HU Xiao-xuan1,2， ZHU Wai-ming1,2， MA Hua-wei1,2

(1.SchoolofManagement,HefeiUniversityofTechnology,Hefei230009,China;

2.AircraftNetworkSystemInstitute,HefeiUniversityofTechnology,Hefei230009,China)

Abstract:A staged task planning method is put forward to solve the task planning problem of satellite and aerostat cooperative reconnaissance. The satellite and aerostat cooperative task planning is divided into three stages that are task clustering, task groups allocation and task scheduling. Firstly, a hierarchical clustering algorithm is used in task clustering by which several task groups would be produced. Secondly, the planning model of task group allocation which aims to build connections between task groups and resources is introduced. At last, a mixed integer planning model used in task scheduling is modeled and a corresponding particle optimize algorithm is introduced. By task scheduling, all tasks would be finally allocated to the specific platforms. The simulation results show that the proposed method is feasible and efficient.

Keywords:satellite; aerostat; cooperative reconnaissance; clustering; mission planning

作者简介：

中图分类号：V 19

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2015.07.15

基金项目：中央高校基本科研业务费专项资金(2012HGZY0009)资助课题

收稿日期：2014-05-29；修回日期：2014-08-13；网络优先出版日期：2014-10-19。