偏微分高程图环境蚁群算法的三维路径规划

肖秦琨, 王　弋, 罗艺闯

(西安工业大学电子信息工程学院, 陕西 西安 710021)



偏微分高程图环境蚁群算法的三维路径规划

肖秦琨, 王弋, 罗艺闯

(西安工业大学电子信息工程学院, 陕西 西安 710021)

摘要：针对在三维空间路径规划中建模与避障问题,提出了一种新的在偏微分高程建模环境下蚁群算法的三维路径规划方法。首先,利用抽象建模和高程建模方法分别构建三维空间环境,并用偏微分对高程环境进行最优数据提取,在此基础上利用高程数学建模方法进行三维空间重建,最终形成偏微分高程环境。其次,首次将种群对于环境的最佳适应度值作为目标函数评判蚁群寻找最优路径的决策能力。最后,在不同的建模环境中应用蚁群算法进行路径寻优,输出最优路径。通过对仿真结果和实验数据分析,验证了所提方法的有效性和正确性。

关键词：偏微分高程建模建模; 蚁群算法; 抽象建模; 三维路径规划; 建模与避障

0引言

三维路径规划的建模方法和路径规划算法是机器人野外作业面临的关键技术难题[1-3],针对这个问题,许多学者进行了深入的探索,并取得了一系列研究成果[4-5]。

为了解决机器人在三维空间环境中路径规划问题,一些研究者提出了高程建模思想[6-7]。核心理论是利用二维栅格先将三维空间环境数据离散化,再将三维空间环境数据所对应的2.5维地形高度信息存入每一个相对应二维栅格中,进而整个三维空间环境的地形特征将被存储在各个区域中。文献[8-9]通过对三维空间环境中较大曲率的地形信息数据点进行提取,并对连续多幅的三维空间场景进行扫描匹配,最终将多足机器人所在的三维空间环境用高程图进行表示。文献[10]在高程建模的三维空间环境中,提出了通过概率定位算法进行行星探测器的设计。文献[11]将市区路面、陆岛以及空间环境中的障碍物用高程图进行表示,然后对其进行检测。文献[12]提出一种基于拓扑高程模型的三维环境建模方法,进行路径规划。

蚁群算法[13]是受蚂蚁的集体觅食行为及在觅食过程中具有其独特优势的启示,提出的一种模仿蚁群觅食过程的算法。通过实验观察发现,尽管个体蚂蚁在觅食过程中的觅食行为比较简单,但是蚁群却能够在实时复杂多变的外部环境中将其所具有的群体行为能力出色地发挥出来,它们不但能通过蚁群所具有的独特的行为能力——将大于自身大小成十上百倍的食物安全完整地送回自己的巢穴,而且蚁群一旦在觅食途中遇到障碍物,蚁群便能够很迅速地重新找到一条能够到达目标点的最优路径。

在通过对高程建模以及蚁群算法的研究基础上,本文提出一种结合偏微分高程建模与蚁群算法的三维路径规划方法,该方法的优势在于:①能够将在抽象建模和高程建模方法中出现冗余的空间数据通过偏微分高程数学方法进行极值化处理,从而能够对三维空间环境的主要信息进行更简单明了地表述。②与抽象建模方法、高程建模方法相比,通过对蚁群适度值的计算并将所获取的数据进行二次曲线拟合输出,以此能够显示出在偏微分高程环境下,蚁群在进行路径规划过程中具有更强的目标决策能力,以及对外部环境的适应能力,并且输出的路径更为安全合理,避障效果更好。③通过计时函数对于时间资源消耗的计算,可以得出在偏微分高程建模方法下蚁群算法的所消耗的时间资源最少。

1三维空间抽象建模

在三维空间地图中建立以左下角的顶点为坐标原点O,经度、纬度增加的方向分别为x轴、y轴,空间高度增加的方向为z轴的三维空间坐标系。在所建立的三维空间坐标系中取点O为坐标原点,ON为x轴所对应经度增加方向上的最大长度,OO′为y轴所对应纬度增加方向上的最大长度,OP为z轴所对应空间高度增加方向上的最大长度。最终,形成三维空间立方体区域OPMN-O′P′M′N′,即蚁群算法将要在该三维空间区域内进行路径规划[14]。

当三维空间路径规划区域构建起来之后,从所建立的三维空间区域OPMN-O′P′M′N′中,将该三维空间区域利用等分方法对三维空间路径规划时所需的搜索数据点进行提取。先将三维空间区域在经度增加方向(x轴延伸方向)的最大长度ON进行n等分,得到n+1个平面Πi(i=1,2,…,n),然后再将所形成的n+1个平面沿y轴延伸方向的最大长度OP进行m等分,然后沿z轴延伸方向最大长度OO′进行l等分,最后,利用抽象建模的数学方法,求解出里面的交点,如图1所示。

图1　三维空间抽象建模空间图与平面图

通过以上步骤,立体的三维路径规划区域OPMN-O′P′M′N′就离散化为一个三维空间数据点的集合,而且每一个数据点都有两个坐标与其相对应,即编号坐标q1(i,j,k) (i=0,1,…,n; j=0,1,…,m; k=0,1,…,l)和位置坐标q2(xi,yi,zi),其中,i,j,k分别为当该点当前所对应的划分编号。蚁群算法将在通过抽象建模方法构建的三维空间环境中的这些空间数据点上进行路径寻优,最终输出一条从起点到目标点并且满足某项最优路径输出指标的最优路径。

为了方便解决在构建的三维空间进行路径规划,本文设定坐标轴原点为路径规划区域内的最低点0,并将该点作为对应的平面环境视为海平面高度,设定高度为600 m的平面为主要进行路径规划陆地平面;在z轴延伸方向上,将高度区域(0,2 km),以100 m为高度差进行等分;在(x,y)平面内,分别在x轴和y轴的延伸方向上,将平面区域(21 km,21 km)以1 km为距离差进行等分。首先通过抽象建模方法建立一个区域跨度为 21 km×21 km×2 km的三维空间不平坦路面环境的仿真图。其次,在上述所建立的三维空间区域内,保持海平面高度和主要进行路径规划的陆地平面不变,将在x轴延伸方向上(5 km,9 km)平面范围内,所对应的z轴延伸方向上的高度值设置为600 m;在y轴延伸方向上(3 km,19 km)平面范围内,所对应的z轴延伸方向上的高度值设置为600 m,最终利用抽象建模方法构建一条三维空间平坦路面，如图2、图3所示。

图2　抽象建模三维空间不平坦路面

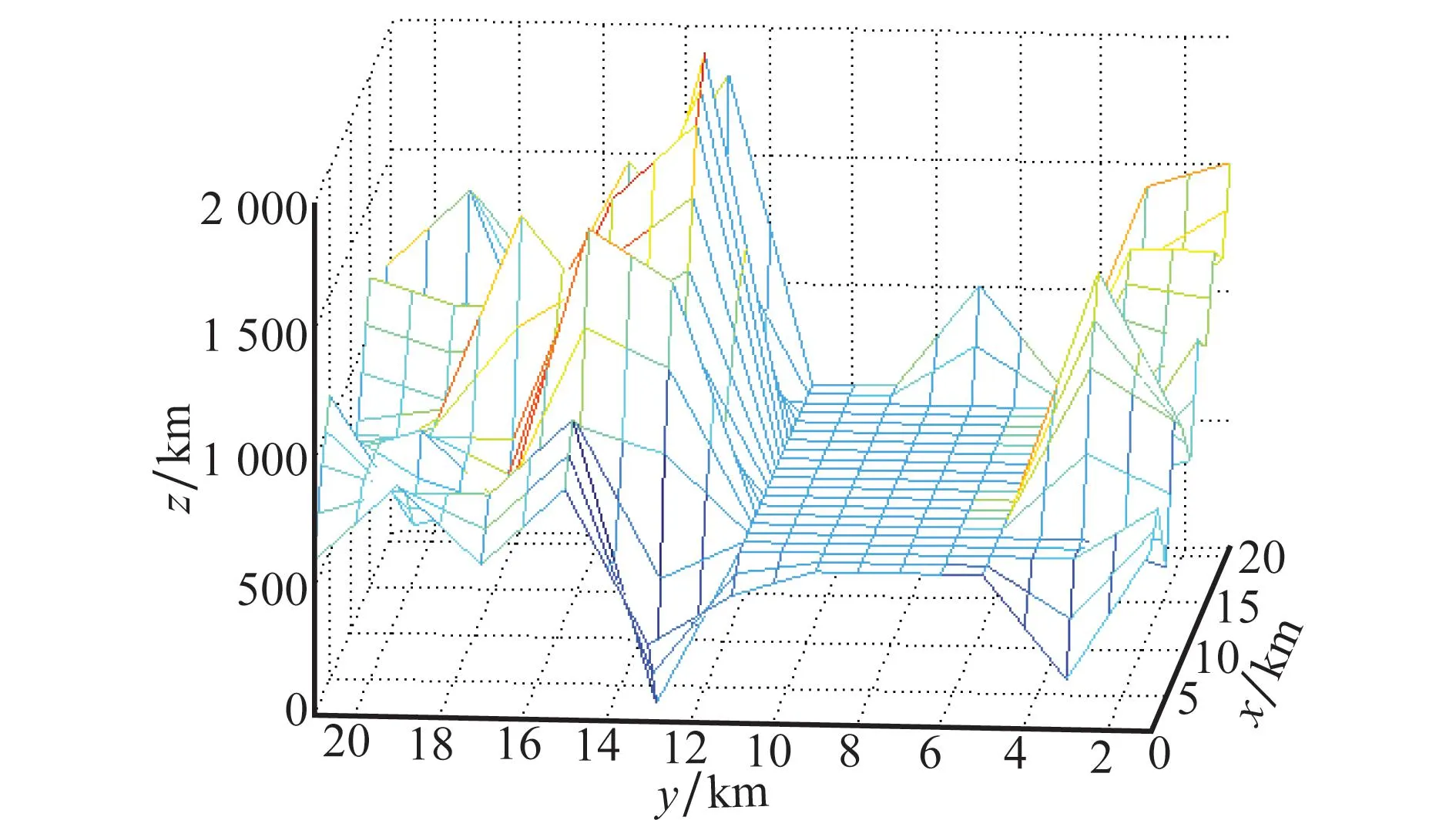
图3　抽象建模三维空间平坦路面

2三维空间高程与偏微分高程建模

2.1三维空间高程建模

2.1.1场景栅格划分

假设设定xy平面内所有通过激光采集的数据点的分布服从相互独立的正态分布f(x,y)~(μ,σ2):

(1)

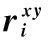
(2)

式中,xc,yc是所采集空间区域内激光数据点的期望值。那么通过某一激光数据点ri对与其相应的栅格Cij的影响程度的计算,则将该激光数据点标定为该栅格内与之相对应的第h个数据点。最后通过大量的参数赋值运算,可以计算出每一组通过激光采集到的数据点ri={r1,r2,…,rn}对与其相对应的栅格影响度μh={μ1,μ2,…,μn}。将影响程度大于阈值μthreshold的点存入栅格中,便完成了将三维空间激光数据点存入与之相对应的栅格的过程。通过对激光点ri所在栅格cij中对应的μ进行规一化处理,可知栅格的高度值由栅格中所有激光点高度的加权平均得出,即

(3)

2.1.2可行区域划分

根据栅格内激光数据点在高度方向上的分布情况,可以计算每个栅格Cij的平均高度:

(4)

从而可以通过计算每两个栅格之间的高度差,以此来获得在某一激光数据采集区域内道路的平坦程度并判断这一区域是否可行。判断某一区域是否可行,栅格间的高度差需满足公式:

(5)

式中,Hij为栅格Cij所在区域的平均高度；Hthresh为根据无人地面自主战车自身情况所设定的阈值。此过程不对邻域空闲栅格进行计算。

根据以上公式,利用高程建模方法形成如图4所示的高程环境。

图4　高程建模环境图

2.2三维空间偏微分高程建模

由式(2)和式(3)可以获取某一时间点在高程建模环境内通过激光采集的空间点数据,然后通过偏导求极值的数学计算,利用偏微分高程数学方法进行空间数据采集,以获取最优数据,计算过程如下:

(6)

(7)

--------------------式中

则可以根据极值公式,求得最优解进而可以求出最优的数据集合。偏微分高程建模环境的可行区域划分根据栅格内激光点在高度方向上的分布情况,可以计算每个栅格Cij的平均高度:

(8)

从而可以通过计算每两个栅格之间的高度差,以此来获得在某一激光数据采集区域内道路的平坦程度并判断这一区域是否可行。判断某一区域是否可行,栅格间的高度差需满足公式:

(9)

式中,Hij为栅格Cij所在区域的平均高度；Hthresh为根据机器人自身情况所设定的阈值。此过程不对邻域空闲栅格进行计算。

根据以上公式,利用偏微分高程图建模方法形成如图5所示的偏微分高程图环境。

3蚁群算法的三维空间路径规划

在上述3种不同的建模方法所建立的三维空间环境中,应用蚁群算法进行路径规划。

步骤 1蚁群通过启发函数来计算到达下一个搜索点的概率,并判断该点是否可行。启发函数为

(10)

式中,D(i,j,k)w1为蚂蚁移动的两个搜索点之间距离,促使其选择与当前所在节点距离较近的搜索点;S(i,j,k)w2为安全因子,当搜索节点无法到达时,该值为0,促使其选择可以达到的搜索点;Q(i,j,k)w3为下一点到终点的距离长度,促使其选择到目标点距离更近的点;w1、w2、w3为系数,代表上述各因素的重要程度。

图5　偏微分高程建模环境图

蚂蚁在平面Πi上的当前点pi选择平面Πi+1上下一个点pi+1:

(11)

式中,τa+1,u,v为平面Πi+1上点p(i+1,u,v)的信息素值。

步骤 2信息素更新:蚁群算法将三维环境搜索空间的散点wi={w1,w2,…,wn}作为节点进行搜索。

信息素的更新包括局部更新和全局更新两部分,局部更新能够使蚂蚁对未经过搜索的节点的搜索概率增加,以达到全局搜索的目的。局部信息素的更新会随着蚂蚁对搜索点搜索同时进行更新,信息素更新公式为

(12)

式中,τijk为点(i,j,k)上所带的信息素值;ξ为信息素的衰减系数。

全局更新是指当蚂蚁对一条路上所有数据点完成搜索以后,将所搜索路径的长度设定为评价值,从该次蚁群所输出的所有路径中,选择其中搜索路径长度最短路径,增加搜索路径长度最短路径上各搜索点的信息素值,信息素更新公式为

(13)

式中,length(m)为第m只蚂蚁移动过的距离长度;ρ为信息素更新系数;K为常量系数。Δτijk为两点之间留下的残留信息素浓度。

当完成一次全局路径规划后,蚁群就会在路径集合中选择出一条最优路经。

步骤 3通过蚁群在不同建模环境适应度值的计算与提取输出最优路径。蚁群对三维空间各个路径搜索点适应度值大小的选择,体现了蚁群寻找最优路径时的决策能力,适应度值越小,说明选择该条路径越合理。当蚁群经过每一个搜索点时,蚂蚁会保存该搜索点所对应适应度值,蚁群对三维环境的适应度值计算公式为

(14)

式中,D(i,j)表示蚁群通过两个搜索点时路径的长度;H(i,j,k)为该搜索点所对应空间的高度值。

当蚁群算法在不同的建模环境下进行路径规划时并且经过若干次迭代后,输出最优路径(即最佳适应度值所对应的路径)。适应度值越小,表明蚁群的决策能力越强,输出的路径越安全合理。

4实验结果及数据分析

在Matlab环境下采用计时函数(计时函数可以定量计算完成制定程序所消耗的时间资源)计算出蚁群从相同起点到目标点在不同建模环境下所消耗的时间资源。通过对适应度值(适应度值越小,路径规划时的决策能力越强、避障效果更好,输出的最优路径更为合理)的计算,并将所有最佳适应度值提取利用最小二乘法曲线拟合的输出,从曲线图中可以体现出蚁群在最优路径寻找过程中的决策能力和避障效果。

4.1三维路径规划步骤及仿真结果

在本次实验中取不平坦路面环境,平坦路面环境,高程建模不平坦路面环境,高程建模平坦路面环境,偏微分高程建模不平坦路面环境和偏微分高程平坦路面等6种不同建模环境的起点为starty=10,starth=3;终点为endy=9,endh=3;蚁群算法的初始参数设置为:w1=3,w2=1,w3=2,K=120,空间离散点n=21,蚂蚁移动步长m=1,蚂蚁在(x,y)平面内进行一次寻优过程的最大纵向和横向移动距离为2,迭代次数为100次。在不同的种群数量和信息素参数下进行试验,①信息素ρ=0.9,种群数量PopNumber=10;②信息素ρ=0.7,种群数量PopNumber=10;③信息素ρ=0.5,种群数量PopNumber=10。

4.1.1仿真结果

图6~图11分别为在参数ρ=0.9,种群数量PopNumber=10时,抽象建模不平坦路面(见图6)、抽象建模平坦路面(见图7)、高程建模不平坦路面(见图8)、高程建模平坦路面(见图9)、偏微分高程建模不平坦路面(见图10)、偏微分高程建模平坦路面(见图11)中所输出的最优路径。

图6　抽象建模不平坦路面路径规划图

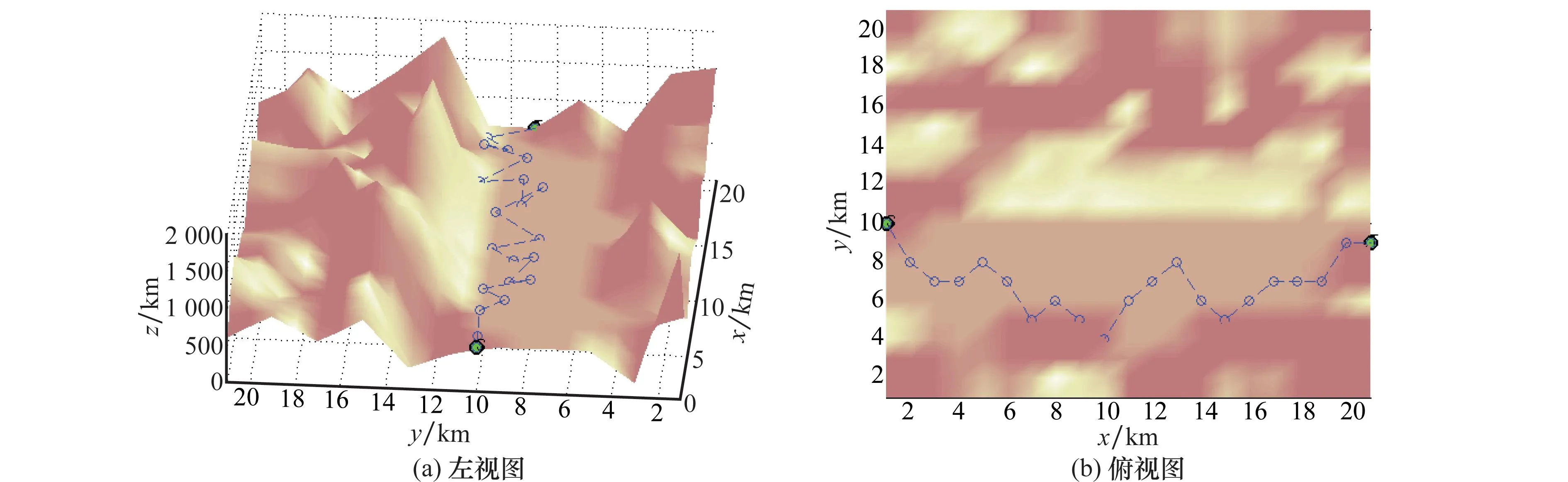
图7　抽象建模环境平坦路面路径规划图

图8　高程建模环境不平坦路面路径规划图

图9　高程建模环境平坦路面路径规划

图10　偏微分高程建模环境不平坦路面路径规划图

图11　偏微分高程建模环境平坦路面路径规划

图12~图17分别为在参数ρ=0.7,种群数量PopNumber=10时,抽象建模不平坦路面(见图12)、抽象建模平坦路面(见图13)、高程建模不平坦路面(见图14)、高程建模平坦路面(见图15)、偏微分高程建模不平坦路面(见图16)、偏微分高程建模平坦路面(见图17)中所输出的最优路径。

图12　抽象建模环境不平坦路面路径规划图

图13　抽象建模环境平坦路面路径规划图

图14　抽象建模环境不平坦路面路径规划图

图15　高程建模环境平坦路面路径规划图

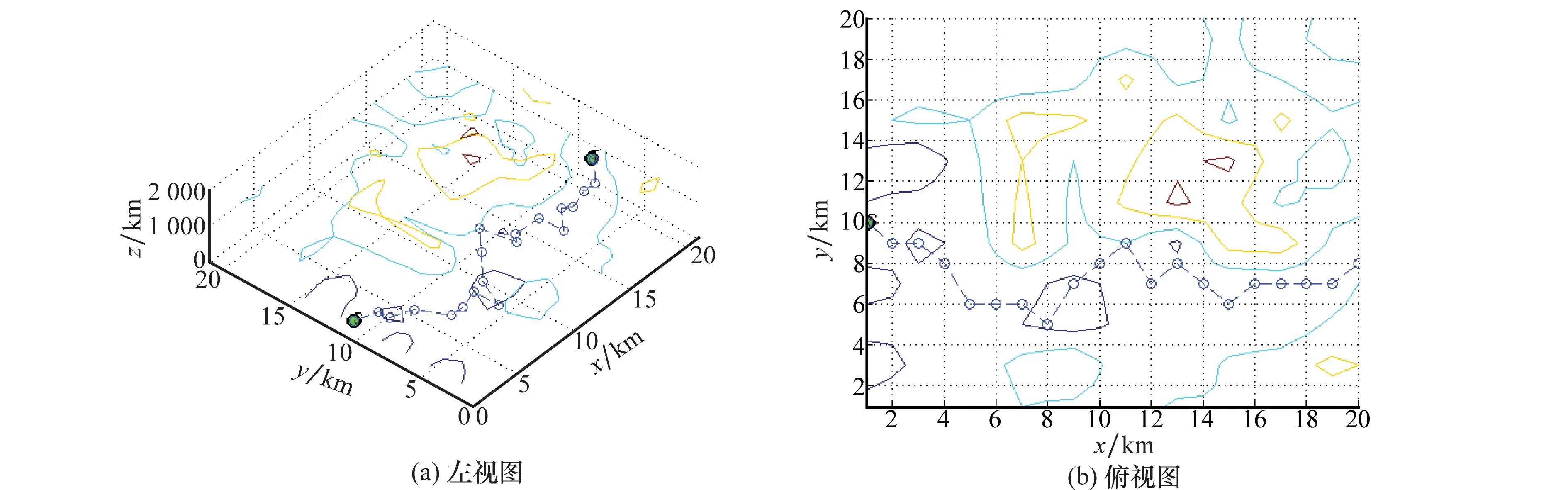
图16　偏微分高程建模环境不平坦路面路径规划图

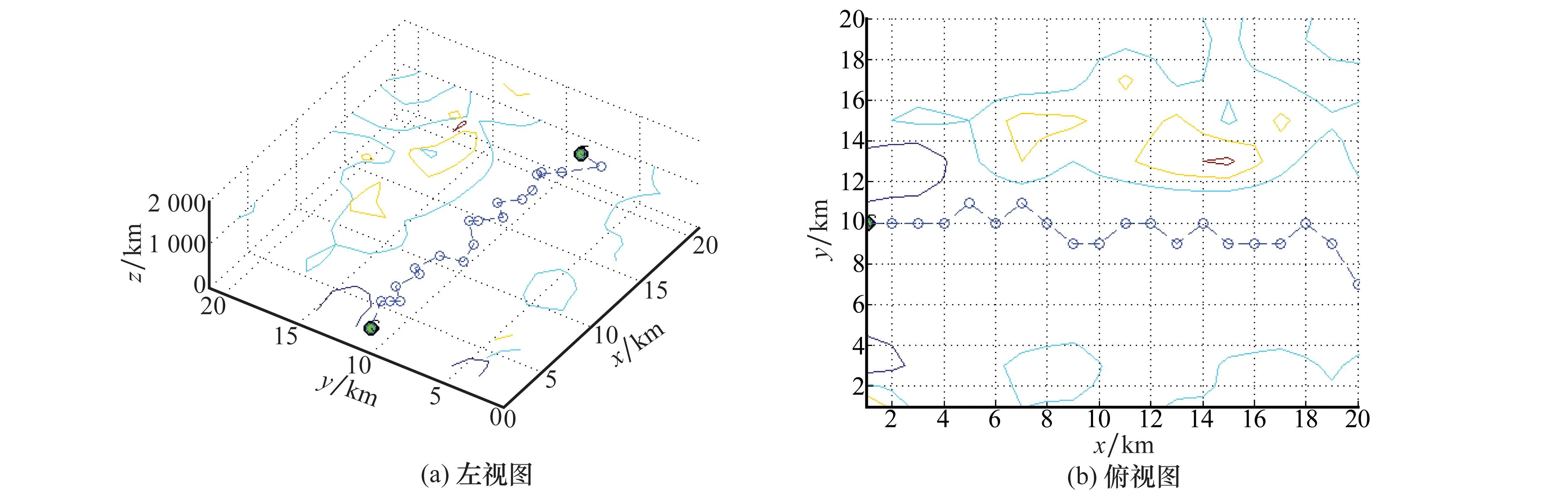
图17　偏微分高程建模环境平坦路面路径规划图

图18~图23分别为在参数ρ=0.5,种群数量PopNumber=10时,抽象建模不平坦路面(见图18)、抽象建模平坦路面(见图19)、高程建模不平坦路面(见图20)、高程建模平坦路面(见图21)、偏微分高程建模不平坦路面(见图22)、偏微分高程建模平坦路面(见图23)中所输出的最优路径。

图18　抽象建模环境不平坦路面路径规划图

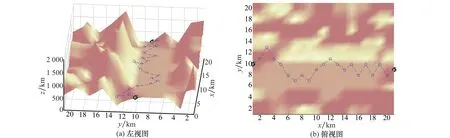
图19　抽象建模环境平坦路面路径规划图

图20　高程建模环境不平坦路面路径规划图

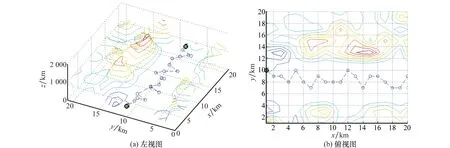
图21　高程建模环境平坦路面路径规划图

图22　偏微分高程建模环境不平坦路面路径规划图

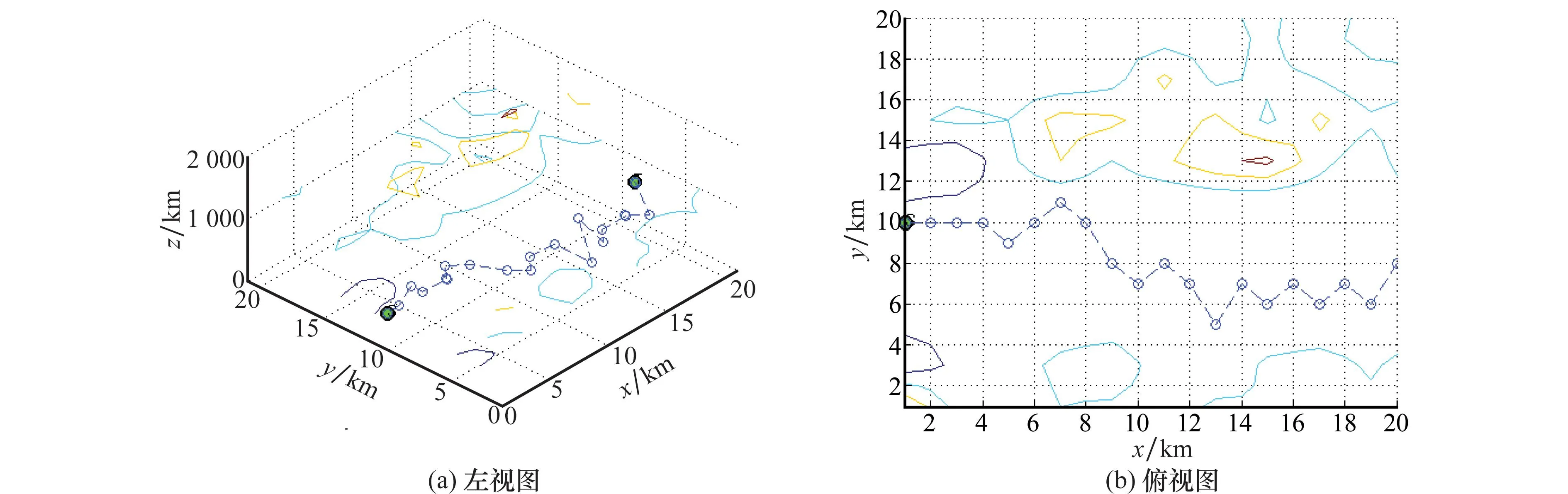
图23　偏微分高程建模环境平坦路面路径规划图

4.1.2实验数据

在6种不同的路面环境中进行路径规划时,将最佳适应度值作为目标函数,并利用时间函数计算在上述不同建模环境的路径规划下所消耗的时间资源,验证了所提方法的有效性和可行性。实验数据如图24~图26和表1所示。

图24　种群适应曲线(ρ=0.9)

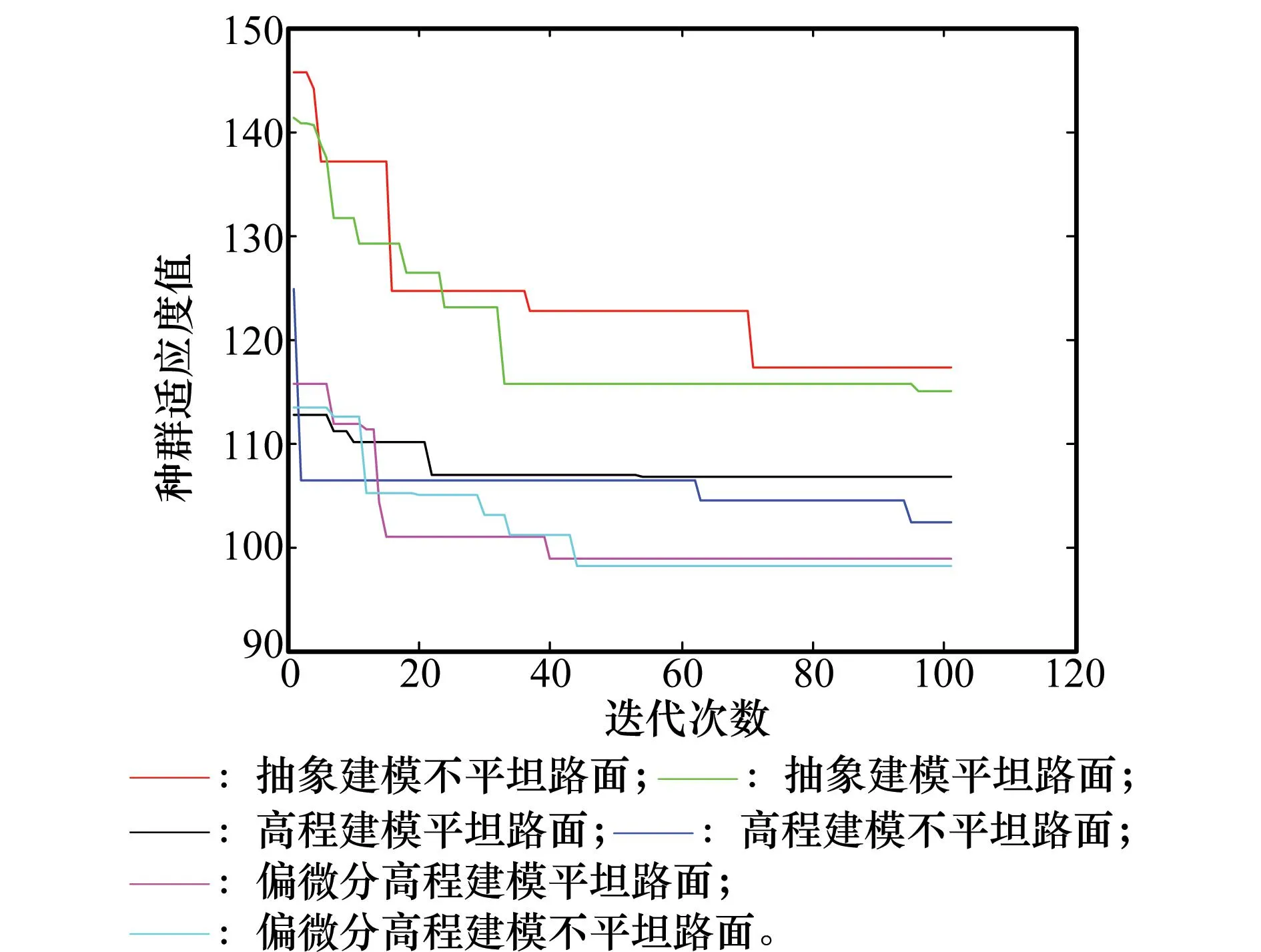
图25　种群适应曲线(ρ=0.7)

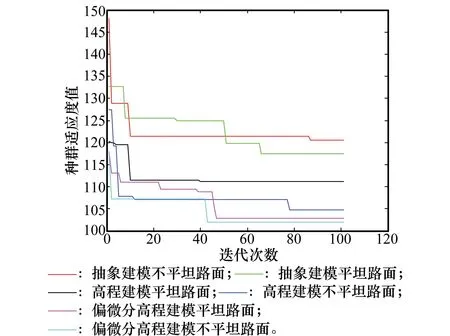
图26　种群适应曲线(ρ=0.5)

4.2实验数据分析

首先,通过表1实验数据的对比,可以看出在信息素大小不同,蚁群数量相同的情况下,偏微分高程环境中进行路径规划是所消耗的时间资源要比在抽象建模和高程建模环境下少。并且实验数据也可以得出信息素挥发程度的大小对于路径规划结果会产生重要的影响。通过对大量相关资料研究与分析,当ρ=0.5时,蚁群算法在二维平面环境下,找寻最优路径时所消耗的时间最短。但通过对本文的实验数据分析可知,当ρ=0.9时,蚁群算法在抽象建模环境中寻找到最优路径耗时最短,而当ρ=0.7,蚁群算法在高程建模和偏微分高程建模环境下,寻找到最优路径所用时间最少。综上所述,在不同的建模方法所建立的三维环境中,信息素的大小会对蚁群算法的路径规划结果产生影响。

其次,通过图24~26可知,种群的最佳适应度值所获取的数据拟合曲线可知,当同种群数目、不同信息素大小时,在偏微分高程建模环境中,蚁群算法在寻找最优路径过程中,种群的适应度值在经过若干次迭代后,所产生的适应度值最小即表明,在此过程中蚁群的适应能力最好,以及对于最优路径选取的决策能力最强,从而使得蚁群输出一条避障效果最好并且能够安全到达目标点的路径。

表1　相同种群数目、不同信息素浓度(PopNumber=10,ρ=0.9,0.7,0.5)情况下的时间资源的消耗

然而,在实验过程中发现,在偏微分高程建模环境和高程建模环境中,蚁群在不平坦路面进行路径寻优时所用时间比相同建模环境中平坦路面进行路径寻优时所用的时间少。该实验结果与当初预想的实验结果和在抽象建模环境中不平坦路面和平坦路面所得出的实验结果完全相反。后大量实验对该结果进行验证,得出此结果并不只是偶然在某一个信息素或者蚁群数量的一次路径规划过程中在才产生的,而是在整个建模环境中。由此可以得出一个结论:不同的建模方法或方式会对信息素的挥发程度产生影响,而信息素的挥发程度会对蚁群算法最后的寻优结果产生影响。

综上所述,在偏微分高程建模方法下构建的三维空间场景相比于高程建模和抽象建模方法构建的三维空间场景所利用的存储空间量小,所表达的空间环境信息更明了。所以,蚁群在寻找目标点时对环境的适应能力、目标点的决策能力更好,并且所消耗的时间更少。因此，蚁群在偏微分高程建模环境中进行三维路径规划时所输出的路径最优及避障效果更好,从而验证了所提方法的有效性。

5结论

本文重点对三维空间环境建模和在三维空间环境建模基础上蚁群算法的路径规划问题进行了研究。本文提出一种新的偏微分高程建模环境下蚁群算法的三维路径规划方法,该方法解决了以下问题:①将在抽象建模和高程建模方法中出现冗余的空间数据,通过对空间数据采集过程中信息数据进行偏微分的极值化处理,获得最优空间信息数据,从而对三维空间环境的主要信息进行简单明了的表达。②提高了蚁群在路径规划过程中对于环境的适应能力、寻找最优目标点的决策能力,并且在整个路径规划中,输出了更为安全合理并且避障效果更好的路径。③减少了蚁群算法在路径规划过程中所需要时间资源的消耗。

通过在Matlab环境下的仿真实验的结果和数据分析,验证了在偏微分高程建模环境下,蚁群在进行三维空间的路径规划时,具有更好的环境适应、决策寻优的能力,并且需要消耗的时间资源更少。此外蚁群所输出的路径更为安全合理,避障效果更好。

在实验过程中发现,在复杂的完全未知的环境进行路径规划时,蚁群的可视点的数目,直接对其能否进行路径规划产生决定性的影响,所以下一步工作,将重点对蚁群算法在复杂的、完全未知的三维空间道路环境中的可视点数量与可视区域进行研究，从而完善蚁群算法在更为复杂的信息完全未知三维空间环境中进行路径规划研究。

参考文献：

[1] Zhou B, Dai X Z, Han J D. Real-time 3D outdoor environment modeling for mobile robot with a laser scanner[J].Robot, 2012, 34(3):321-328.(周波,戴先中,韩建达.基于激光扫描的移动机器人3D室外环境实时建模[J].机器人,2012,34(3):321-328.)

[2] Xu A Q, Chatavut. Optimal complete terrain coverage using an unmanned aerial vehicle[C]∥Proc.oftheIEEEInternationalConferenceonRoboticsandAutomation,2011:2513-2519.

[3]Nationalresearchcouncilofthenationalacademies.Technologydevelopmentforarmyunmannedgroundvehicle[M]. Fu M Y, Wang M L, trans.Beijing: National Defense Industry Press,2008.(军用无人地面车辆技术的发展[M].付梦印,王美玲,译.北京:国防工业出版社,2008.)

[4] Lartigue C, Quinsat Y, Mehdi-Souzani C.Voxel-based path planning for 3D scanning of mechanical parts[J].Computer-AidedDesignandApplications,2014,11(2):220-227.

[5] Olivieri P, Birglen L, Maldague X, et al. Coverage path planning for eddy current inspection on complex aeronautical parts[J].RoboticsandComputer-IntegratedManufacturing,2014,30(3):305-314.

[6] Ye C.Borenstein J.A novel filter for terrain mapping with laser rangefinders[J].IEEETrans.onRobtics,2004,20(5):913-921.

[7] Plagemann C,Mischke S,Prentice S,et al. A Bayesian regression approach to terrain mapping and an application to legged robot locomotion[J].JournalofFieldRobotics,2009,26(10):789-811.

[8] Olson C F. Probabilistic self-localization for mobile robots[J].IEEETrans.onRoboticsandAutomation, 2000,16(1):55-66.

[9] Oniga F, Nedevschi S. Processing dense stereo data using elevation maps: road surface, trafficisle and obstacle detection[J].IEEETrans.onVehicularTechnology,2010,59(3):1172-1182.

[10] Olson C F. Probabilistic self-localization for mobile robots[J].IEEETrans.onRoboticsandAutomation,2000,16(1):55-66.

[11] Oniga F, Nedevschi S. Processing dense stereo data using elevation maps: road surface, traffic isle and obstacle detection[J].IEEETrans.onVehicularTechnology,2010,59(3):1172-1182.

[12] Yan F, Zhuang Y, Bai M, et al. 3D outdoor environment modeling and path planning based on topology-elevation model[J].ActaAutomaticaSinica,2010,36 (11):1493-1501.(闫飞,庄严,白明,等.基于拓扑高程模型的室外三维环境建模与路径规划[J].自动化学报，2010,36(11):1493-1501.)

[13] Dorigo M, Maniezzo V, Colorni A. The ant system: optimization by a colony of cooperating agents[J].IEEETrans.onSystems,ManandCybernetics,PartB:Cybernetics,1996,26(1):29-41.

[14] Shi F, Wang H, Yu L, et al. 30samplesofMATLABintelligentalgorithm[M]. Beijing：Beihang University Press,2011:229-236.(史峰,王辉,郁磊,等.MATLAB 智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011:229-236.)

肖秦琨(1974-),男,教授,博士,主要研究方向为动态贝叶斯网络及多媒体信息检索。

E-mail:xiaoqinkun10000@163.com

E-mail:wangyi860205@126.com

罗艺闯(1987-),男,硕士,主要研究方向为模式识别。

E-mail:luoyichuang@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141209.0119.005.html

3D path planning of ant colony algorithm using partial

differential elevation modeling

XIAO Qin-kun, Wang Yi, LUO Yi-chuang

(DepartmentofElectronicsandInformationEngineering,Xi’anTechnologicalUniversity,Xi’an710021,China)

Abstract:A novel three-dimensional (3D) path planning method of the ant colony algorithm under the partial differential elevation modeling is proposed to tackle the problem of scene modeling and obstacle avoidance. Firstly, the 3D abstract scene and elevation scene are built by their modeling respectively, and then the optimal data is extracted from the elevation scene to construct partial differential scene by using the partial differential mathematical method. Furthermore, the best fitness value of the ant colony firstly treated as objective function is employed to display the decision-making capacity of the ant colony in the 3D path planning. Finally, the ant colony algorithm is combined with abstract scene, elevation scene or the partial differential elevation scene, and the best path planning is shown out in 3D scene. Experimental results and statistics analysis show the effectiveness and validity of the proposed algorithm.

Keywords:partial differential elevation modeling; ant colony algorithm; abstract modeling; three-dimensional (3D) path planning ; modeling and obstacle avoidance

通讯作者王弋(1986-),,男,硕士研究生,主要研究方向为无人战车野外路径规划。

作者简介：

中图分类号：V 279

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2015.07.14

基金项目：国家自然科学基金(61271362)；陕西省自然科学基金(2012JM8028)；陕西省教育厅专项科研基金(12JK0510，12JK0727)；中省共建-跨平台研究项目(ZXXM01)资助课题

收稿日期：2014-04-17；修回日期：2014-10-16；网络优先出版日期：2014-12-09。