高效超分辨波达方向估计算法综述

闫锋刚, 沈　毅, 刘　帅, 金　铭, 乔晓林

(1. 哈尔滨工业大学(威海)信息与电气工程学院, 山东 威海 264209;

2. 哈尔滨工业大学航天学院,黑龙江 哈尔滨 150001)



高效超分辨波达方向估计算法综述

闫锋刚1, 沈毅2, 刘帅1, 金铭1, 乔晓林1

(1. 哈尔滨工业大学(威海)信息与电气工程学院, 山东 威海 264209;

2. 哈尔滨工业大学航天学院,黑龙江 哈尔滨 150001)

摘要：高效超分辨波达方向估计算法致力于降低超分辨算法的计算量、节约系统的实现成本、弱化算法对于阵列结构的依赖性,是推进超分辨理论工程化的一个重要研究课题。从多重信号分类(multiple signal classification, MUSIC)算法的原理和构成要素入手,以基于MUSIC派生高效超分辨算法的目的和方法为标准,将现存高效超分辨算法划分为实值运算、波束域变换、快速子空间估计、快速峰值搜索和免峰值搜索5大类。在此基础上,全面回顾总结了各类高效算法的发展历程和最新进展,对比分析了它们的主要优缺点。最后,结合空间谱估计实际工程化的应用需求,指出了高效超分辨算法的未来发展趋势。

关键词：高效超分辨算法; 实值运算; 波束域变换; 快速子空间估计; 快速峰值搜索; 免峰值搜索

0引言

波达方向(direction of arrival, DOA)估计是阵列信号处理的重要研究课题之一[1]。自20世纪70年代至今,该技术经历了一个繁荣的发展阶段,取得了辉煌的研究成果。1986年,美国学者Schmidt提出了著名的多重信号分类(multiple signal classification, MUSIC)算法[2],实现了传统空间谱估计向超分辨测向的飞跃,成为空间谱估计发展历史上的一个重要里程碑。

然而随着应用的深入,人们发现以MUSIC为代表的超分辨算法在实际应用中普遍存在稳健性差[3]、计算量大[4]、对阵列结构依赖性强[5]等缺陷。这些缺陷与超分辨近乎完美的理论性能形成了鲜明对比,促使空间谱估计研究热点由最初对算法性能的不懈追求逐渐转向为对超分辨理论实际工程化的研究,而高效超分辨算法则是这其中的一个重要研究方向。

高效超分辨算法致力于降低传统算法的计算量、节约系统的实现成本、弱化超分辨理论对阵列结构等外界输入条件的依赖性,是推进超分辨理论工程化的重要环节。由于MUSIC算法开创了超分辨DOA估计的先河,本文从基于MUSIC派生超分辨算法的角度入手,将现存高效超分辨算法划分为实值运算、波束域变换、快速子空间分解、快速峰值搜索和免峰值搜索5大类别。在此基础上,全面总结各类高效算法的兴起、发展和最新研究进展,同时深入对比分析它们的优缺点。最后,结合实际工程化的应用需求,指出高效超分辨算法的未来发展趋势。

1数据模型及MUSIC算法

1.1典型一维数据模型

不失一般性,本文以一维数据模型为例展开论述,相关推导和结论可直接扩展到二维情形。

常用典型一维DOA估计数据模型可表示为

(1)

式中,N为快拍数;x(t)∈CM×1,s(t)∈CL×1及n(t)∈CM×1分别是接收数据、入射信号及高斯白噪声向量；A(θ)[a(θ1),a(θ2),…,a(θL)]∈CM×L是导向矢量矩阵且导向矢量a(θ)定义为

(2)

阵列接收数据协方差矩阵定义为

(3)

式中,S为信号协方差矩阵;σ2为高斯白噪声功率。对R进行特征值分解,可得

(4)

式中,λi(i=1,…,L)和λj(j=L+1,…,M)分别为R的L个大特征值及M-L个小特征值；ei和ej分别为λi和λj对应的特征矢量。定义矩阵

(5)

则Es和En的列分别张成信号子空间和噪声子空间。可以证明[2]:span(Es)⊥span(En)且span(Es)=span(A)。实际应用中,理想R无法获得,可以用N快拍数据对其进行估计，即

(6)

1.2MUSIC算法

根据信号子空间与噪声子空间的正交性可知,在信号入射方向θ,有aH(θ)En=0。由此,可构造MUSIC空间谱函数

(7)

在[-π/2,π/2]内搜索,使fMUSIC(θ)出现极大值的入射角θ即为信号DOA,这就是MUSIC算法。

MUSIC的提出开创了超分辨DOA估计的崭新时代,掀起了世界众多学者对于超分辨空间谱估计的研究热潮,成为了空间谱发展历史上的一个重要里程碑。

虽然MUSIC实现了真正的超分辨测角,但其计算量通常很大。庞大的计算量使超分辨理论在实际工程、尤其是对实时性要求较高的工程中的应用变得异常困难。为了推进超分辨理论的工程化进度,学者们不得不对高效超分辨算法展开研究。

2高效超分辨算法分类

伴随空间谱估计30余年的发展,高效超分辨算法取得了丰硕的研究成果。为了准确、清晰地认识这些算法的发展历程和最新进展,本节首先对MUSIC的计算量进行分析,接着对以MUSIC为算法原型、派生高效算法的方法进行归纳分析,最后对现存主流高效超分辨算法进行分类,从而为后文高效超分辨算法分类综述奠定基础。

2.1MUSIC计算量分析

2.2基于MUSIC派生高效算法的方法

由于子空间估计和峰值搜索是MUSIC的两个最主要计算单元,故从计算量构成的角度可得到“MUSIC≈子空间估计+峰值搜索”的近似等式。此等式有利于对以MUSIC为基本算法原型、派生高效算法的方法进行归纳。

由上述等式易见:可通过如下3方面方法实现超分辨算法的高效性:

(2) 降低峰值搜索的计算量。峰值搜索通常是一个多维(包含1维)的参量联合遍历过程,因此该类方法的出发点集中在以下3方面:一是降低峰值搜索的维度(如从2维搜索降低到1维搜索);二是压缩峰值搜索的参量范围;三是彻底避免峰值搜索。

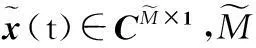
需要强调的是,上述3类高效化方法虽然来源于对MUSIC计算量的分析,但它们同样可对其他超分辨算法实现高效性。另外,可以连续使用不同方法实现高效性,如实值旋转不变子空间(unitaryestimatesignalparameterviarotationalinvariancetechnique,U-ESPRIT)算法先以上述第(2)方面方法避免了峰值搜索,又以第(3)方面方法实现了实值化[8]。

2.3高效超分辨算法分类

根据上述分析,选取MUSIC为基本算法模型,以从MUSIC派生高效超分辨算法的目的(目的层)和方法(方法层)角度入手,对现存高效超分辨算法进行分类和划分,结果如图1所示。

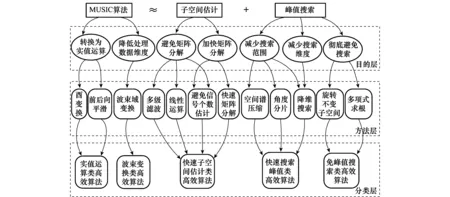
图1　高效超分辨算法分类

图1中的各类算法相对于MUSIC处理流程的分布关系如图2所示。由图2可见:不同类别的算法在实际应用中可能存在交叉。然而,从基于MUSIC派生高效算法的角度对现存高效超分辨算法分类,有利于全面认识高效算法的发展,也有利于对不同机理的算法性能进行对比分析。下文对各类高效算法分别展开综述。

图2　5类算法相对于MUSIC流程的分布

3实值运算类高效算法

3.1超分辨算法实值化方法

3.1.1酉变换

酉变换是当来波信号非相干时,对超分辨算法进行实值化的代表性技术,该技术由Huarng和Yeh于1991年首次提出[9]。他们观察发现:在诸如均匀线阵(uniform linear array, ULA)这样的中心对称阵(centro-symmetric array, CSA)中,导向矢量a(θ)具有中心对称性

(8)

式中,φ(θ)为相位差;J为反对角矩阵。

基于式(8)可以证明:当信号协方差阵RS是一个对角矩阵,即来波信号非相干时,式(3)给出的协方差阵R是一个艾米特中心对称阵(centro-Hermitianmatrix,CHM)。由此,可对R进行变换

(9)

其中,当M为偶数时,U矩阵定义为

(10a)

当M为奇数时,U矩阵定义为

(10b)

3.1.2前后向平滑

(11)

3.2实值算法研究进展

继酉变换和FB之后,实值类高效算法得到了世界各国学者的广泛关注并取得了丰硕的研究成果。

文献[8]基于CSA提出了U-ESPRIT算法,在降低运算量的同时获得了优于ESPRIT的估计精度，同时，利用U-ESPRIT解决了非圆信号(若信号s与其任意旋转sejφ具有相同的一阶矩和二阶矩则称s为非圆信号)DOA估计[11]及多维谐波恢复问题[12]。文献[13]对实值类算法进行了全面、深入的研究，针对U-ESPRIT对DOA估计可能失败的缺点,提出了基于伪噪声采样的改进算法,同时将传统DOA估计技术(method of direction estimation, MODE)和root-MUSIC实值化,提出了U-MODE[14]和U-root-MUSIC算法[15],还利用理论分析和实测声纳、超声波数据证实了实值类算法比复值类算法估计性能更好。文献[16]提出了一种U-ESPRIT频率估计算法,新算法相比于经典ESPRIT在不牺牲算法精度的同时极大地降低了算法复杂度。文献[17]利用投影映射建立了z平面上半圆与实值区间[-1,1]的对应关系,进而提出了ULA下的U-root-MUSIC算法。文献[18-19]基于CSA先后提出了U-MVM算法和实值矩阵束(unitary matrix pencil, U-MP)算法,在降低计算量的同时获得了更高的测角精度。

近年来,实值类算法的研究热点正逐渐由不同算法的实值化转向为算法在具体系统的应用,但相关报道很少。2011年,文献[20]提出了适用于电控无源阵列天线(electronically steerable parasitic array radiator, ESPAR)的实值U-RD-MUSIC算法。2012年,文献[21]提出了适用多输入多输出(multiple input multiple output, MIMO)雷达系统的U-MUSIC算法。

一般而言,超分辨算法的复杂度和估计精度是难以调和的一对矛盾,这意味着超高的估计精度是以巨额的计算开销为代价的。然而,实值类算法实现了低复杂度和高精度的双赢,因而是高效超分辨发展历史上具有重要意义的研究成果。然而不幸的是,现存实值类算法几乎都是基于CSA结构提出的,当阵列不满足中心对称时,它们也不再适用,如表1所示。

表1　实值类算法优缺点及发展趋势

上述分析可见:推导适用于任意阵列的高效实值类算法是高效超分辨领域亟待解决的难题。在此方面,笔者近年来提出了半实值DOA估计的概念[22]。半实值算法可实现与实值算法相同的计算效率,同时能适用于任意阵列结构,为实值算法向任意阵列结构的过渡提供了理论参考。

4波束域变换类高效算法

BS域变换是实现超分辨算法高效性的另一重要方法。需要注意的是,这里所说的BS域变换与自适应波束形成(adaptive beam-forming, ABF)[23]不同。ABF通过对各阵元加权实现空域滤波,而BS域变换通过对接收数据降维实现算法复杂度的降低,其基本原理如图3所示。其中,x(t)和y(t)分别为ES域天线真实输出数据和BS域虚拟变换数据,且二者满足

(12)

式中,B∈CM×T为波束形成矩阵;T为波束数。

由于x(t)∈CM×1,y(t)∈CT×1且T≤M,因此BS域变换能把R阵分解和谱峰搜索的计算量分别从O(M3)和O(JM2)降低到O(T3)和O(JT2)。

图3　波束域变换基本原理[79]

BS变换最早由美国学者Bienvenu[24]和德国学者Byrne[25]提出。文献[24]发现在传统ES域算法前端对阵元输出数据进行BS变换,能降低超分辨算法对阵元误差的灵敏度;文献[25]发现在以EVD为基础的超分辨方法前端进行BS变换,能得到感兴趣区域的稳定DOA估计。

随后,一些学者尝试着将高分辨算法运用到BS域。著名学者Lee[26]和Zoltowski[27]分别对ES域MUSIC和root-MUSIC算法进行了研究并分别提出了BS-MUSIC和BS-root-MUSIC算法。近年来,文献[28，30]分别推导出了适用于MIMO的BS-ESPRIT和BS-WSF算法。文献[29]用统一的形式分析了这几种算法的性能,用一个简单的表达式通过基阵阵列流形和波束形成矩阵等物理量表示了这些算法对方位估计的均方误差(mean square error, MSE),讨论了使方位估计MSE最小的波束形成矩阵B的设计准则。

BS域算法大多都采用了数据降维处理,把原本以阵元数为维数的方位估计问题转换为以波束数为维数的估计问题。这种维数的降低,是波束域方法运算量下降的基础。维数的降低本质上使得天线阵观测的空间区域变小,也使得阵列空间原本完整的输出数据信息被部分丢弃。因此,BS域算法的估计准确度和精度必然受到影响。

一般而言,BS域算法估计精度与波束数目及位置有关,然而无论怎样选取波束形成矩阵B,大多数BS域算法的克拉美罗下界(Cramer-Raolowerbound,CRLB)总是不小于ES域算法的CRLB[30]。事实上,为了正确地估计信号入射角,BS域算法通常需要假定待测信源在某个特定的角度分片之内。因而,BS域算法通常需要信号入射角的先验信息。研究发现:只有当待测信源在先验已知的入射角度分片内时,BS域算法才具有与ES域算法相同的CRLB[30]。

5快速子空间估计类高效算法

快速子空间估计类算法致力于提高信号子空间或噪声子空间的估计效率,进而降低超分辨算法的计算量。由于子空间估计常R矩阵分解实现,因此该类方法的出发点要么是以快速算法降低矩阵分解的计算量,要么是选取替代方案彻底避免矩阵分解。

5.1快速矩阵分解类算法

为了降低R分解的计算量,学者们提出了许多快速子空间估计算法,主要包括传播算子(propagator method, PM)算法[31]、梯度算法[32]、幂迭代算法[33]及由文献[34]基于Lanczos算子提出的快速子空间分解(fast subspace decomposition, FSD)算法。其中,PM和FSD算法效果最为明显。PM利用线性运算代替EVD和SVD运算,能够快速得到子空间分解值,较好地降低了算法的计算量。FSD在大阵元数、小信源数的DOA估计问题中具有非常明显的计算效率优势,其复杂度约为

(13)

通常M>L,因此相比于传统方法O(M3)的计算量,FSD能大幅降低协方差矩阵分解的计算量。

FSD算法的前提是假设R已知,而以接收数据估计R仍需较大计算量,故研究无需R估计的快速子空间估计方法很有意义。为此,文献[35]利用多级维纳滤波器在最小均方意义下得到了Wiener-Hopf方程的最优解,实现了无需R估计的快速子空间估计方法,同时有效降低了R分解的复杂度。

5.2免矩阵分解类算法

为了彻底避免矩阵分解,许多无需矩阵分解的高效算法应运而生。文献[6]利用二维L型ULA组合阵列,以L型阵列间相关协方差矩阵线性运算估计噪声子空间,避免了矩阵分解。文献[36]在最小二乘准则下建立了线性预测方程组,通过求解该方程组的解获得信号子空间的标准正交基,从而避免了繁杂的矩阵分解运算。理论分析和实验表结果明,该方法可获得与MUSIC相当的估计性能。文献[37]基于ULA的旋转不变性,提出了一种无需特征值分解的子空间类算法(subspace-basedmethodwithouteigendecomposition,SUMWE)。该算法通过子阵平均和子阵互相关处理,以线性运算快速估计噪声子空间,同时较好地克服了信号相关对于DOA估计的影响。

免矩阵分解快速子空间估计算法以线性运算代替矩阵EVD或SVD分解迭代过程,大大降低了算法的复杂度。然而不幸的是,此类算法大多建立在特殊的信号或阵列结构假设之上。另外,这类算法通常也只能得到信号子空间或噪声子空间的近似值,精度相对较差。

一般而言,子空间估计的计算量与阵元数M的平方成正比,谱峰搜索的计算量与空间谱采样点数J成正比。由于J≫M,故子空间估计的计算量远小于空间谱峰值搜索的计算量。因此,减少或者彻底避免空间谱峰值搜索是实现超分辨算法高效性的关键。

6快速搜索类高效算法

快速搜索类算法以降低搜索参量维度、压缩搜索参量范围、避免搜索过程等方式实现超分辨算法的高效性。

6.1降维搜索类算法

降维处理类算法多应用于多维参数的联合估计,其目的是将多维搜索降低为有限个一维搜索,从而降低算法的复杂度。这类算法意义重大,但研究成果十分有限。

文献[6]基于L型ULA组合阵列,以L型阵列间相关协方差矩阵线性运算估计噪声子空间,然后基于两个一维搜索实现高精度二维DOA估计。相比于2D-MUSIC算法,该方法较好地提高了算法在低信噪比和小快拍数下的估计性能。文献[38]针对MIMO中离开角(directionofdepart,DOD)和DOA联合估计问题,利用噪声投影矩阵的可逆性提出了降维MUSIC(reduceddimensionMUSIC,RD-MUSIC)算法,将2D-MUSIC算法中的二维搜索化简为一次一维搜索,极大地降低了复杂度。随后,文献[39]讨论了RD-MUSIC算法的角度取值情况,进一步缩小了搜索范围。文献[40]针对多通道DOA和到达时间(timeofarrival,TOA)联合估计问题,提出了基于树结构的TST-MUSIC算法,将二维搜索转换为3次一维搜索。在此基础上,文献[41]提出了FSF-MUSIC算法,用3次一维搜索解决二维DOA和信号频率联合估计问题;文献[42]同样基于树结构思想提出了用于2D-DOA联合估计的新算法,同时分析了算法的理论性能。

尽管上述几种不同的降维搜索类算法已在实际应用中提高了DOA估计的效率,但遗憾的是,这些算法均或多或少地对算法的适用情景进行了限定,如表2所示。因此,如何基于一般阵列结构对多维搜索类算法实现降维处理,依然是空间谱估计领域亟待攻克的一个理论难题。

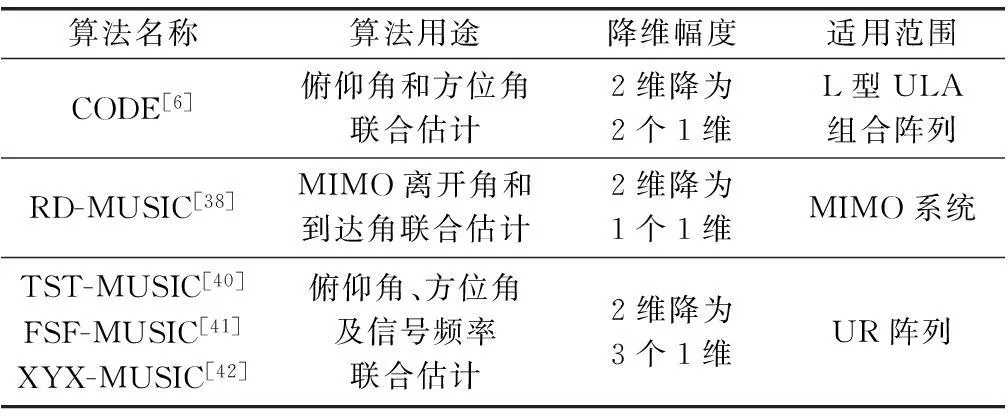
表2　典型降维搜素类算法对比

6.2分片搜索类算法

分片搜索类算法的目的是将多维谱峰搜索的参量范围从整个参量空间缩小到某一感兴趣的小参量分片内,从而有效地降低算法的复杂度。这类算法常需要借助特殊的阵列结构或预知的信号入射角先验信息。

现存的主流分片搜索类算法主要有两类,一是基于FFT的改进算法[43];二是基于BS域变换的数据降维处理算法[24-30]。前者依据ULA下阵列输出的均匀相移性质,先以FFT形成多个波束,初步确定可能的DOA范围,再利用MUSIC算法在初估计范围内搜索,最终得到高精度DOA估计值。后者已在前文进行了论述。

近年来,笔者基于参量分片思想提出了全新的高效压缩谱理论(spectral compression theory, SCT),并发展了一系列高效超分辨DOA估计算法[7,44-47]。相比于FFT改进算法及BS域降维算法,SCT具有无需角度先验信息、适用任意阵列结构、具有更低噪声子空间维度、同时适用1D-DOA和2D-DOA估计等诸多优点。

7免搜索类高效算法

免搜索类算法通过彻底避免繁杂的谱峰搜索过程降低算法的计算量,其典型代表即为由文献[48]提出的旋转不变子空间(estimation of signal parameters via rotational invariance techniques, ESPRIT)算法以及由文献[49]提出的求根MUSIC(root-MUSIC)算法。

7.1旋转不变子空间类算法

当阵列存在导向矢量分别为A1(θ)和A2(θ)的两个子阵且A1(θ)和A2(θ)满足

(14)

所示的旋转不变性时,即可用ESPRIT避免峰值搜索。与MUSIC不同,ESPRIT是信号子空间类算法,它利用阵列信号子空间之间的旋转不变特性进行信号参数估计,直接得到信号DOA估计的闭式解,从而降低算法的复杂度[48]。

考虑到ESPRIT仍需对R进行EVD或SVD分解,其计算量依然较大。为了进一步降低ESPRIT子空间估计的复杂度,学者们提出了许多低复杂度改进算法。

国外方面,文献[50]基于PM算子从阵列接收数据中快速提取噪声子空间,而文献[51]通过求解线性最小均方问题获得了信号子空间基。文献[52-54]利用R的离散傅里叶变换(discreteFouriertransform,DFT)获取了信号子空间特征向量。虽然这些方法与ESPRIT相比降低了计算的复杂度,便利了算法的实时处理,然而它们均需要较多的先验知识,这大大限制了算法的扩展性。

国内方面,文献[55]利用R的幂估计噪声子空间,然后对噪声子空间进行QR分解并使用R估计信源个数。由于利用了QR分解且噪声子空间矩阵的维度比R的维度更低,因此,新算法降低了复杂度。文献[56]基于共轭梯度算法和矩阵-向量之间的线性运算方法实现了信号子空间的快速估计。另一方面,文献[57-58]利用MIMO系统的信号特性,分别基于虚拟阵列和矩阵降维思想提出了高效ESPRIT算法。

ESPRIT及其改进算法相比于MUSIC类算法虽然极大地降低了复杂度,同时在信号频率估计中表现出了优于MUSIC类算法的性能(见文献[59]第4.7节),但大多数ESPRIT类算法都是建立在阵列结构的旋转不变性之上的,因此该类算法的应用范围相比于MUSIC类算法较小。

7.2多项式求根类算法

root-MUSIC是求根类高效算法的典型代表。虽然是MUSIC在ULA下的推广,然而理论分析[60]和实验结果[14]均表明:root-MUSIC的估计精度比MUSIC更优。由于root-MUSIC仅适用于ULA,故将经典root-MUSIC推广到任意阵阵列结构成为了该类算法的研究热点。

就目前研究成果而言,在任意阵列结构下借助多项式求根实现快速DOA估计的技术主要有阵列内插(arrayinterpolation,AI)、流形分离(manifoldseparationtechnique,MST)及频域求根(Fourier-domainrootMUSIC,FD-root-MUSIC),如图4所示。

图4　任意阵列求根的主要实现方式

7.2.1阵列内插

AI最早由美国学者Friedlander[61]提出,其基本出发点是通过阵列变换使得任意阵列的导向矢量a(θ)具有范德蒙结构,即

(15)

式中,b1(θ)是具有M1个阵元的虚拟ULA的导向矢量;Ψ1是设计的内插矩阵。由于b1(θ)具有范德蒙结构,故可基于内插后的虚拟ULA,以多项式求根进行DOA估计。

寻求高效、变换误差小的阵列内插方法是AI技术的研究热点。文献[62]针对2D-CA阵列提出了用于2D-DOA估计的新算法。新算法利用两次阵列内插得到平移不变子阵,然后利用子阵关系得到俯仰角,最后利用一维搜索得到方位角,降低了AI转换误差,但计算量有所增加。文献[63]提出了一种Toeplitz-Introduced变换算法,该算法将NULA转换为ULA并利用root-MUSIC和ESPRIT估计信号DOA,有效提高了算法的估计性能。文献[64]根据信源分布的先验信息,将AI技术与数据降维联合应用,提出了一种低复杂度DOA估计算法。文献[65]将圆阵(circular array, CA)转化为ULA且保持阵元间距为半波长,通过阵列孔径增加思想提出了一种内插算法,克服了传统变换方法将CA转换为ULA时分辨率不高的缺点。

7.2.2流形分离

MST是近年来出现的另一种将求根类算法推到任意阵列结构的新方法。该方法由意大利青年学者Belloni[66]提出,其基本思想来源于20世纪90年代末产生的波形建模公式[67]。MST基本观点是将任意阵列导向矢量a(θ)近似分裂成两个独立部分的乘积

(16)

式中,Ψ2只与阵列结构参数有关；b2(θ)仅与信号DOA有关且可等效为一个具有M2个阵元的虚拟ULA的导向矢量。因此,b2(θ)与信号DOA有关且具有范德蒙结构。由于信号DOA包含于具有范德蒙结构的b2(θ)之中,故可利用该部分以多项式求根估计DOA。

与AI相比,MST无需进行角度区间分割,故其变换误差更小。另外,MST的所有信号处理均是在ES域进行的,这避免了BS域变换与生俱来的映射误差。然而,MST为了达到足够精度,需对阵列流形互耦、天线误差、阵元取向和阵元位置等非理想因素进行校正。与AI相似,MST在得到近似多项式后,基于root-MUSIC估计信号DOA的精度与该多项式的阶数密切相关。通常,阶数M2需按式(17)准则选取以保证足够估计精度:

M2≈4kQ

(17)

式中,k是信号波数;Q是阵列最大孔径。大阶数M2的选取使得MST常需对远大于阵元数的多项式求根。例如,对一个16阵元德URA,MST需对阶数高达55的多项式求根[68]。因此,MST复杂度改善未必十分明显。

目前,对MST研究成果较少。国外方面,文献[69]分析了MST的理论性能,给出了以MST进行DOA估计的“渐进”MSE封闭表达式。文献[70]提出了基于MST的2D-DOA估计算法,在无需精确已知导向矢量的条件下以多项式求根得到俯仰角和方位角估计值。国内方面,文献[71]对MST性能进行了全面仿真分析,揭示了MST性能主要取决于信噪比(signal-to-noise ratio, SNR)和模式数的基本事实。文献[72]将MST采样矩阵的求取转化为最小二乘问题,以root-MUSIC算法解决非均匀圆阵(non-uniform CA, NUCA)下的DOA估计问题。文献[73]将MST和PM综合,解决了2D-UCA下DOA估计精度因阵元数减少而下降的难题。

7.2.3频域求根

FD-root-MUSIC由德国学者Rübsamen[68]提出,其利用了如下数学事实:任意阵列结构下的MUSIC空间谱函数fMUSIC(θ)是关于信号入射角θ的周期函数,其周期为2π,即

(18)

众所周知,任何一个周期函数都可近似表示为无限长度的傅里叶级数。由于傅里叶级数具有范德蒙结构,故可利用多项式求根实现快速DOA估计。FD-root-MUSIC据此将MUSIC空间谱表示为无限长度的傅里叶级数,然后基于一定准则对该级数进行如式(19)所示的截断。

(19)

式中,系数Fm可通过数据填充和FFT求解得到。

业已证明:在相同截断长度下,即M2=M3时,FD-root-MUSIC具有比MST更好的估计精度[68]。由于FD-root-MUSIC对无限长傅里叶级数进行了有限截断,因此该级数的阶数通常需要取值很大以保证足够的近似精度,而高阶多项式求根复杂度依然很高。为了克服该缺点,文献[74]基于傅里叶级数的劳伦结构对FD-root-MUSIC进行了改进,新算法在保持估计精度不下降的同时,降低了多项式的求根阶数,减少了算法的复杂度。目前,尚未见FD-root-MUSIC算法在2D-DOA估计中的研究报道。

除root-MUSIC之外,求根类算法还包括root-WSF[75]、root-SUMWE[76]、root-MNM[77]以及root-Capon[78]等,由于这类算法的原型都是针对ULA提出的,因此,可用AI和MST技术来对这些算法的适用阵形进行扩展。

需要强调的是:求根类DOA估计算法常以迭代方法求解多项式的根,因此该类算法的计算效率会受求根多项式阶数(由阵元数决定)的显著影响,如图5所示。仿真平台及仿真条件如下：Intel(R) Core(TM)2 Duo CPU, 2 GHz, 1 GB内存,半波长ULA,快拍数100,信噪比10 dB,信号DOA为30°和50°,MUSIC谱峰值搜索步长为0.005 3°。

图5　仿真时间与阵元数关系

由图5可见，当阵元数较大时,相比于搜索类算法,求根类算法的计算效率未必突出。因此,对于root-MUSIC、root-MNM、root-WSF等经典求根算法以及A1、MST、FD-root-MUSIC等新型技术,它们在工程应用中均会面临如何快速求根的问题。因此,根据空间谱估计的具体理论模型和应用背景,研究适合于快速DOA估计的求根类算法的“实现”方法,是目前亟待解决的一个理论问题。

8典型算法仿真分析

本节对上述5类高效超分辨算法中具有代表性的典型算法进行计算机仿真分析和对比。由于这5类算法都具有超分辨性能和高计算效率,因此实验重点考察和对比分析各类算法的估计性能和计算效率。

实验选取的典型算法为:实值运算类算法U-MUSIC[9]、波束域变换类算法BS-MUSIC[26]、快速子空间估计类算法SUMWE-MUSIC(先以SUMWE估计噪声子空间,后以MUSIC估计DOA)[37]、快速峰值搜索类算法C-MUSIC[45]和免峰值搜索类算法ESPRIT[48]。其中,BS-MUSIC角度变换区域为20°~40°,波束数为T=6,波束形成矩阵B按BS5方法计算(详见文献[79]第4.4.1节)。C-MUSIC压缩倍数为β=2。各仿真结果均为1 000次Monte-Carlo统计均值。

8.1不同算法的估计性能对比

图6给出了利用6种高效算法进行DOA估计的MSE值随SNR的变化对比曲线。为了强化比较,实验同时引入MUSIC[2]和无限制CRLB[80]作为性能参考。实验参数设置如下：12阵元半波长ULA,快拍数为200,信号数为2,DOA为30°和50°。谱搜索步长0.005 3°。

图6　估计精度与信噪比关系

由图6可见:

(1) 6种算法中,U-MUSIC估计精度最高,其在低信噪比下也表现出非常接近于CRLB的估计性能。事实上,类似结论已从同类超分辨算法的复值版本和实值版本比较中获得[8-9,14-15]。因此,实值类算法实现了计算高效性和估计高精度的双赢[22]。

(2) ESPRIT的估计精度均差于其他5类算法。考虑到ESPRIT相比于搜索类算法避免了峰值搜索,相比于求根类算法避免了高阶多项式求根,故ESPRIT是5类快速算法中以精度换取低复杂度最为高效的一种算法[22,45,48]。

(3) BS-MUSIC、SUMWE-MUSIC和C-MUSIC的精度相当且接近于MUSIC。随着SNR提高,3种高效算法的MSE均趋向于CRLB,故这3类高效算法在降低计算量的同时,未引起估计精度的过大牺牲[26-27,45,79]。

8.2不同算法的计算效率对比

图7给出了6种算法的仿真时间随阵元数的变化关系。仿真平台及仿真条件如下：Intel(R) Core(TM)2 Duo CPU, 2 GHz, 1 GB内存,ULA,快拍数200,信噪比10 dB,信号DOA为30°和50°,搜索类算法搜索范围20°~40°,搜索步长0.005 3°。

图7　仿真时间与阵元数关系

由图7可见:

(1) 5种高效算法相比于MUSIC均大幅提高了算法的计算效率。当阵元数较大时,这种计算效率优势越发明显；

(2) 由于彻底避免了峰值搜索[47],ESPRIT相比于其他5类搜索类算法表现出最为明显的计算效率优势；

(3) U-MUSIC借助实值变换减少了约75%计算量[9],其计算效率在5种搜索类算法中最高；

(4) C-MUSIC将搜索范围进行了β倍压缩且相比于其他5类搜索类算法降低了噪声子空间的维度[45],故其表现出仅次于U-MUSIC的计算效率[22]；

(5) BS-MUSIC和SUMWE-MUSIC分别降低了数据的维度和子空间估计的计算量,但未减少峰值搜索范围[26,37],故二者的计算效率相当并略差于C-MUSIC。

由上述仿真分析可见:大多数高效超分辨算法在降低算法计算量的同时,较好保持甚至提高了算法的估计性能。然而需要注意的是,相比于经典MUSIC,这些高效算法或多或少地引入了一定的假设条件。例如,U-MUSIC等实值运算类算法需要阵列满足中心对称性,BS-MUSIC等波束域变换变换类算法需假定待估计DOA位于特定角度区域之内,SUMWE等快速子空间估计类算法依赖于阵列结构的旋转不变性;C-MUSIC等快速搜索类算法对阵元数有更强限制(M>βL)[45]。因此,在工程应用中,应根据实际条件灵活选择各类高效算法。

9结束语

空间谱估计技术经过了近30年的蓬勃发展,已经取得了异常辉煌的研究成果,然而实际工程化的不断深入使得学者们不得不将研究的重心由最初对算法性能的无限追求不断转化到算法在实际工程应用中的落实中来。因此,如何在复杂环境中快速、有效地进行多源信号测向仍是目前亟待解决的一大难题。

本文全面回顾总结了高效超分辨算法的发展历史和最新进展,分析对比了实值运算、波束域变换、多项式求根及子空间4大类高效超分辨算法的优缺点。基于上述分析不难看出,在超分辨算法的高效性方面仍有以下问题亟待学者们深入研究:

(1) 任意阵列结构下的降维搜索类算法。在许多实际应用中,常会以计算量庞大的多维空间搜索联合估计入射信号的频率、极化、DOA、TOA等参数。虽然近年来产生了一些降维搜索类算法,但其或多或少地对阵列结构进行了限定。近年来,笔者提出了压缩谱理论,较好地解决了任意阵列结构下的高效超分辨DOA估计问题,但其相比于降维搜索算法的高效性仍有一定距离。因此,适用于任意阵列结构的降维搜索算法是超分辨领域亟待攻克的一个理论难题。

(2) 任意阵列结构下的实值类算法。实值类算法相比于复值类算法实现了低复杂度和高精度的双重收益,然而现存的实值算法几乎都是基于CSA结构提出的,这极大地限制了实值类算法的应用范围。近年来,笔者提出了适用于任意阵列结构的半实值类超分辨算法,在实值化算法的阵列结构普适性方面迈出了过渡性的一步,但目前仍未见任意阵列结构下的实值类算法报道,因此该方面工作仍然需要深入研究。

(3) 求根类算法的实际工程化。在实际工程中,常常需借助迭代算法求解多项式的根,进而估计信号DOA。因此,求根类算法在实际工程应用中必然均会面临如何快速求根的问题。一般而言,迭代计算因受初值设置和迭代方法的影响常会出现迭代费时、收敛错误甚至不收敛的问题。因此,如何根据空间谱估计的具体应用背景,提出高效、稳健的求根类DOA估计算法实现途径是需要解决的一个实际问题。

参考文献：

[1] Krim J, Viberg M. Two decades of array signal processing[J].IEEESignalProcessingMagazine, 1996, 13(4):67-94.

[2] Schmidt R O. Multiple emitter location and signal parameter estimation[J].IEEETrans.onAntennasandPropagation, 1986, 34(3): 276-280.

[3] Zeng W J, So H C, Huang L.lp-MUSIC: robust direction of arrival estimator for impulsive noise environments[J].IEEETrans.onSignalProcessing, 2013, 61(17): 4296-4308.

[4] He Z Q, liu Q H, Jin L N, et al. Low complexity method for DOA estimation using array covariance matrix sparse representation[J].ElectronicsLetters, 2013, 49(3): 228-230.

[5] Ying D W, Yan Y H. Robust and fast localization of single speech source using a planar array[J].IEEESignalProcessingLetters, 2013, 20(9):909-912.

[6] Wang G M, Xin J M, Zheng N N, et al. Computationally efficient subspace-based method for two-dimensional direction estimation with L-shaped array[J].IEEETrans.onSignalProcessing, 2011, 59(7): 3197-3212.

[7] Yan F G, Jin M, Qiao X L. Source localization based on symmetrical MUSIC and its statistical performance analysis[J].ScienceinChinaseriesF:InformationSciences, 2013, 56(6):062307(13).

[8] Haardt M, Nossek J A. Unitary ESPRIT: how to obtain increased estimation accuracy with a reduced computational burden[J].IEEETrans.onSignalProcessing, 1995, 43(5):1232-1242.

[9] Huarng K C, Yeh C C. A unitary transformation method for angle of arrival estimation[J].IEEETrans.onSignalProcessing, 1991, 39(3): 975-977.

[10] Linebarger D A, DeGroat R D, Dowling E M. Efficient direction finding methods employing forward-backward averaging[J].IEEETrans.onSignalProcessing, 1994, 42(8): 2136-2145.

[11] Roemer F, Haardt M. Multidimensional unitary sensor-ESPRIT for non-circular sources[C]∥Proc.oftheInternationalConferenceonAcoustics,Speech,andSignalProcessing(ICASSP), 2009:3577-3580.

[12] Steinwandt J, de Lamare R C, Haardt M. Knowledge-aided direction finding based on Unitary ESPRIT[C]∥Proc.ofthe5thAsilomarConferenceonSignals,SystemsandComputers(ACSSC), 2011:613-617.

[13] Gershman A B, Haardt M. Improving the performance of unitary ESPRIT via pseudo-noise resampling[J].IEEETrans.onSignalProcessing, 1999, 47(8): 2305-2308.

[14] Pesavento M, Gershman A B, Haardt M. Unitary root-MUSIC with a real-valued eigendecomposition: a theoretical and experimental performance study[J].IEEETrans.onSignalProcessing, 2000, 48 (5):1306-1314.

[15] Gershman A B, Stoica P. On unitary and forward-backward MODE[J].DigitalSignalProcessing, 1999, 9(2):67-75.

[16] Mahata K, Soderstrom T. ESPRIT-Like estimation of real-valued sinusoidal frequencies[J].IEEETrans.onSignalProcessing, 2004, 52(5): 1161-1170.

[17] Selva J. Computation of spectral and root MUSIC through real polynomial rooting[J].IEEETrans.onSignalProcessing, 2005, 53 (5): 1923-1927.

[18] Kikuma N. Performance analysis of unitary Capon method for DOA estimation with high computational efficiency[C]∥Proc.oftheInternationalSymposiumonAntennasandPropagation(ISAP), 2005:313-315.

[19] Yilmazer N, Koh J, Sarkar T K. Utilization of a unitary transform for efficient computation in the matrix pencil method to find the direction of arrival[J].IEEETrans.onSignalProcessing, 2006, 54(1):175-181.

[20] Akkar S, Gharsallah A. Reactance domains unitary MUSIC algorithms based on real-valued orthogonal decomposition for electronically steerable parasitic array radiator antennas[J].IETMicrowaves,Antennas&Propagation,2012,6(2):223-230.

[21] Zheng G M, Chen B X, Yang M L. Unitary ESPRIT algorithm for bistatic MIMO radar[J].ElectronicsLetters, 2012, 48(3):179-181.

[22] Yan F G, Jin M， Liu S, et al. Real-valued MUSIC for efficient direction estimation with arbitrary array geometries[J].IEEETrans.onSignalProcessing, 2014, 62(6): 1548-1560.

[23] Hang R, Lamare R C. Robust Adaptive beamforming using a low-complexity shrinkage-based mismatch estimation algorithm[J].IEEESignalProcessingLetters, 2014, 21(1): 60-64.

[24] Bienvenu G, Kopp L D. High resolution method sensitivity by conventional beamformer preprocessing[C]∥Proc.oftheInternationalConferenceonAcoustics,Speech,andSignalProcessing(ICASSP),1986:13-20.

[25] Byrne C, Steele A. Sector-focused stability for high resolution array processing[C]∥Proc.oftheInternationalConferenceonAcoustics,Speech,andSignalProcessing(ICASSP), 1987: 2340-2343.

[26] Lee H, Wengrovitz M. Resolution threshold for beamspace MUSIC for two closely-spaced emitters[J].IEEETrans.onAcoustics,SpeechandSignalProcessing,1990,38(9):1545-1549.

[27] Zoltowski M D, Kautz G M, Silverstein S D,et al. Beamspace root-MUSIC[J].IEEETrans.onSignalProcessing, 1993, 41(1): 344-364.

[28] Guo Y D, Zhang Y S, Tong N N. Beamspace ESPRIT algorithm for bistatic MIMO radar[J].ElectronicsLetters, 2011, 47(15):876-878.

[29] Fu L, Liu H. Statistical analysis of beam-space estimation for direction of arrivals[J].IEEETrans.onSignalProcessing, 1994, 42(3):604-610.

[30] Stoica P, Nehorai A. Comparative performance study of element space and beamspace music estimators[J].SignalProcessing, 1991, 10(11): 285-292.

[31] Akkar S, Harabi F, Gharsallah A. Improved reactance domain unitary propagator algorithms for electronically steerable parasitic array radiator antennas[J].IETMicrowaves,Antennas&Propagation, 2013, 7(1):112-116.

[32] Zhuang X B, Cui X W, Lu M Q, et al. Low-complexity method for DOA estimation based on ESPRIT[J].JournalofSystemEngineeringandElectronics, 2010, 21(5): 729-733.

[33] Guo X S, Wan Q, Yang W L, et al. Fast DOA tracking of coherently distributed sources based on subspace updating[C]∥Proc.oftheInternationalConferenceonRadar, 2006:16-19.

[34] Xu G H, Kailath T. Fast subspace decomposition[J].IEEETrans.onSignalProcessing, 1994, 42(3):539-551.

[35] Goldstein J S, Reed I S, Scharf L L. A multi-stage representation of the wiener filter based on orthogonal projections[J].IEEETrans.onInformationTheory,1998,44(7):2943-2959.

[36] Davila C E, Azmoodeh M. Efficient estimation of the signal subspace without eigendecomposition[J].IEEETrans.onSignalProcessing,1994,42(1):236-239.

[37] Xin J M, Sano A. Computationally efficient subspace-based method for direction-of-arrival estimation without eigendecomposition[J].IEEETrans.onSignalProcessing,2004,52(4):876-893.

[38] Hasan M A, Azimi-Sadjadi M R, Hasan A A. Rational invariant subspace approximations with applications[J].IEEETrans.onSignalProcessing, 2000, 48(11):3032-3041.

[39] Zhang X F, Xu L Y, Xu D Z. Direction of departure (DOD) and direction of arrival (DOA) estimation in MIMO radar with reduced-dimension MUSIC[J].IEEESignalProcessingLetters, 2010, 14(12):1161-1163.

[40] Jin H, Swamy M N S, Ahmad M O. Joint DOD and DOA estimation for MIMO array with velocity receive sensors[J].IEEESignalProcessingLetters, 2011, 18(7):399-402.

[41] Wang Y Y, Chen J T, Fang W H. TST-MUSIC for Joint DOA-Delay estimation[J].IEEETrans.onSignalProcessing, 2001, 49(4):721-729.

[42] Lin J D, Fang W H, Wang Y Y, et al. FSF MUSIC for Joint DOA and frequency estimation and its performance analysis[J].IEEETrans.onSignalProcessing,2006,54(12):4529-4542.

[43] Wang Y Y, Lee L C, Yang S J, et al. A tree structure one-dimensional based algorithm for estimating the two-dimensional direction of arrivals and its performance analysis[J].IEEETrans.onAntennasandPropagation, 2008, 56(1):178-188.

[44] Ji Z Y, Yang X H. Improved algorithm of DOA based on FFT and MUSIC[J].JournalofSystemSimulation, 2010, 22(2):487-490.(计征宇, 杨向华. 基于FFT与MUSIC的改进DOA估计算法[J].系统仿真学报, 2010, 22(2):487-490.)

[45] Yan F G, Jin M, Qiao X, et al. Low-complexity DOA estimation based on compressed MUSIC and its performance analysis[J].IEEETrans.onSignalProcessing,2013,61(8):1915-1930.

[46] Yan F G, Liu S, Jin M, et al. Fast DOA estimation based on MUSIC symmetric compressed spectrum[J].SystemsEngineeringandElectronics,2012,34(11):2198-2202.(闫锋刚,刘帅,金铭,等.基于MUSIC对称压缩谱的快速DOA估计[J].系统工程与电子技术, 2012, 34(11):2198-2202.)

[47] Yan F G, Jin M, Qiao X L. Fast 2-D DOA estimation method in transformed domain with arbitrary arrays[J].ActaElectronicaSinica, 2013, 41(5):936-942. (闫锋刚, 金铭,乔晓琳. 适用于任意阵列的变换域二维波达角快速估计算法[J].电子学报, 2013, 41(5):936-942.)

[48] Paulraj A, Roy R, Kailath T. A subspace rotation approach to signal parameter estimation[J].IEEETrans.onSignalProcessing, 1986, 74(6):1044-1046.

[49] Barabell A J. Improving the resolution performance of eigenstructure-based direction-finding algorithms[C]∥Proc.oftheInternationalConferenceonAcoustics,Speech,andSignalProcessing(ICASSP), 1983: 336-339.

[50] Marcos S, Benidir M. On a high resolution array processing method non-based on the eigenanalysis approach[C]∥Proc.oftheIEEEInternationalConferenceonAcoustics,Speech,andSignalProcessing(ICASSP), 1990：2955-2958.

[51] Xin J M, Akira S. Computationally efficient subspace-based method for direction-of-arrival estimation without eigendecomposition[J].IEEETrans.onSignalProcessing, 2004, 52(4):876-893.

[52] Carlos E D, Masoud A. Efficient estimation of the signal subspace without eigendecomposition[J].IEEETrans.onSignalProcessing, 1994, 42(1): 236-239.

[53] Arnab K S, Xia W. Minimum-norm method without eigendecomposition[J].IEEESignalProcessingLetters, 1994, 1 (1):12-14.

[54] Alex B G. Direction of arrival estimation using generalized minimum norm approach[J].ElectronicsLetters, 1991, 27(16): 122-126.

[55] Bao Z Q, Wu S J, Zhang L R, et al. A novel and low complexity ESPRIT method[J].JournalofElectronicsandInformationTechnology, 2007, 29(9): 2042-2046.

[56] Zhuang X B, Cui X W, Lu M Q, et al. Low-complexity method for DOA estimation based on ESPRIT[J].JournalofSystemsEngineeringandElectronics, 2010, 10(5):2042-2046.

[57] Yang M L, Chen B X, Yang X Y. Conjugate ESPRIT algorithm for bisatic MIMO radar[J].ElectronicsLetters, 2010, 46(25):1692-1694.

[58] Zhang X, Xu D. Low-complexity ESPRIT-based DOA estimation for colocated MIMO radar using reduced-dimension transformation[J].ElectronicsLetters, 2011, 47(4): 283-284.

[59] Stoica P, Moses R L.Spectralanalysisofsignals[M].New Jersey: Prentice Hall Press, 2005.

[60] Rao B D, Hari K V S. Performance analysis of root-MUSIC[J].IEEETrans.onAcoustics,SpeechandSignalProcessing,1989，37(12): 1939-1949.

[61] Friedlander B, Weiss A J. Direction finding using spatial smoothing with interpolated arrays[J].IEEETrans.onAerospaceandElectronicSystems, 1992, 28(2):574-587.

[62] Sun X J, Zhang G Y, Tang B, et al. Circle array receiving signal 2D-DOA separable estimation based on twice virtual interpolations[J].JournalofElectronics&InformationTechnology, 2008, 30 (8):1890-1892. (孙学军,张高毅,唐斌,等. 基于二次虚拟内插的圆阵接收2D-DOA分离估计[J].电子与信息学报, 2008, 30(8):1890-1892.)

[63] Ming L A. Toeplitz-induced mapping technique in sensor array processing[J].IEEETrans.onSignalProcessing, 1995, 43 (5):1128-1139.

[64] Qi C Y, Chen Z J, Zhang Y S, et al. Rapid DOA estimation algorithm based on projection pretransformation[J].SystemsEngineeringandElectronics, 2006, 28(4): 525-528.(齐崇英,陈志杰,张永顺,等.基于投影预变换的快速DOA估计算法[J].系统工程与电子技术,2006,28(4):525-528.)

[65] Wang Y L, Chen H, Wan S H. An effective DOA method via virtual array transformation[J].ScienceinChinaSeriesF:InformationSciences,2001,44(1):75-82.

[66] Belloni F, Richter A, Koivunen V. DOA estimation via manifold separation for arbitrary array structures[J].IEEETrans.onSignalProcessing, 2007, 55(10): 4800-4810.

[67] Doron M A, Doron E. Wavefield modeling and array processing, Part II-algorithms[J].IEEETrans.onSignalProcessing, 1994, 42(10): 2560-2570.

[68] Belloni F, Richter A, Koivunen V. Extension of root-MUSIC to non-ULA array configurations[C]∥Proc.oftheInternationalConferenceonAcoustics,Speech,andSignalProcessing(ICASSP), 2006：4-19.

[69] Rubsamen M, Gershman A B. Direction-of-arrival estimation for nonunifom sensor arrays: from manifold separation to Fourier domain music methods[J].IEEETrans.onSignalProcessing, 2009, 57(2): 588-599.

[70] Costa M, Koivunen V, Richter A. Low complexity azimuth and elevation estimation for arbitrary array configurations[C]∥Proc.oftheInternationalConferenceonAcoustics,Speech,andSignalProcessing(ICASSP), 2009:2185-2188.

[71] Zhao C, Yuan Y S. DoA estimaiton via manifold separation technique[J].Science&TechnologyReview, 2008, 26(13): 40-43. (赵超, 袁业术. 基于流行分离的DOA估计算法[J].科技导报, 2008, 26(13): 40-43.)

[72] Lu H J, Zhang X H, Xiong X. Application of manifold separation technique in non-uniform circular array[J].ActaArmamentarii,2011,32(9):10-13.(卢海杰,章新华,熊鑫,等.流形分离在非均匀圆阵上的应用[J].兵工学报,2011,32(9):10-13.)

[73] Pan J, Zhou J J, Jiang F. A fast algorithm of DOA estimation for sparse uniform circular array based on manifold separation technique (MST)[J].JournalofElectronics&InformationTechnology, 2010, 32(4):964-966. (潘捷, 周建江, 汪飞. 基于流形分离技术的稀疏均匀圆阵快速DOA估计方法[J].电子与信息学报, 2010, 32(4): 964-966.)

[74] Zhuang J, Li W, Manikas A. Fast root-MUSIC for arbitrary arrays[J].ElectronicsLetters, 2010, 46(2):174-176.

[75] Hyberg P, Jansson M, Ottersten B. Array interpolation and DOA MSE reduction[J].IEEETrans.onSignalProcessing, 2005, 53(12):4464-4471.

[76] Kenaga H I, Chige K I, Arai H. High-resolution and low-cost DOA estimation by modified Root-SUMWE method[C]∥Proc.oftheInternationalSymposiumonAntennasandPropagation(ISAP), 2012, 8(2): 351-354.

[77] Krim H, Forster P, Proakis J G. Operator approach to performance analysis of root-MUSIC and root-min-norm[J].IEEETrans.onSignalProcessing, 1992, 40(7):1687-1696.

[78] Wu J X, Wang T, Suo Z Y, et al. DOA estimation for ULA by spectral Capon rooting method[J].ElectronicsLetters, 2009,45(1):84-85.

[79] Wang Y L, Chen H, Peng Y N, et al.Spatialspectralestimationtheoryandalgorithm[M].Beijing: Tsinghua University Press, 2009.(王永良,陈辉,彭应宁,等. 空间谱估计理论与算法[M].北京:清华大学出版社, 2009.)

[80] Stoica P, Nehorai A. Performance study of conditional and unconditional direction-of-arrival estimation[J].IEEETrans.onAcoustics,SpeechandSignalProcessing,1990,38(10):1783-1795.

闫锋刚(1982-),男,讲师,博士,主要研究方向为阵列信号处理及统计性能分析。

E-mail:yfglion@163.com

沈毅(1965-),男,教授,博士研究生导师,博士,主要研究方向为智能检测、控制及信号处理。

E-mail:shen@hit.edu.cn

刘帅(1980-),男,副教授,博士,主要研究方向为阵列信号处理。

E-mail:liushuaiboy@163.com

金铭(1968-),男,教授,博士研究生导师,博士,主要研究方向为雷达对抗及阵列信号处理。

E-mail:hit0987@sohu.com

乔晓林(1948-),男,教授,博士研究生导师,博士,主要研究方向为信号处理、无线通信、特种雷达、极化敏感阵列信号。

E-mail:paulqiao@sohu.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141229.1543.001.html

Overview of efficient algorithms for super-resolution DOA estimates

YAN Feng-gang1, SHEN Yi2, LIU Shuai1, JIN Ming1, QIAO Xiao-lin1

(1.SchoolofInformationandElectricalEngineering,HarbinInstituteofTechnologyat

Weihai,Weihai264209,China; 2.SchoolofAstronautics,Harbin

InstituteofTechnology,Harbin150001,China)

Abstract:Computationally efficient methods for super-resolution direction of arrival (DOA) estimation aim to reduce the complexity of conventional techniques, to economize on the costs of systems and to enhance the robustness of DOA estimators against array geometries and other environmental restrictions, which has been an important topic in the field. According to the theory and elements of the multiple signal classification (MUSIC) algorithm and the primary derivations from MUSIC, state-of-the-art efficient super-resolution DOA estimators are classified into five different types. These five types of approaches reduce the complexity by real-valued computation, beam-space transformation, fast subspace estimation, rapid spectral search, and no spectral search, respectively. With such a classification, comprehensive overviews of each kind of efficient methods are given and numerical comparisons among these estimators are also conducted to illustrate their advantages. Future development trends of efficient algorithms for super-resolution DOA estimates are finally predicted with basic requirements of real-world applications.

Keywords:efficient super-resolution algorithm; real-valued computation; beam-space transformation; fast subspace estimation; rapid spectral search; no spectral search

作者简介：

中图分类号：TN 959.2

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2015.07.01

基金项目：山东省自然基金(ZR2014FQ003)；中央高校基本科研业务费专项资金(HIT.NSRIF.2016102);中国博士后科学基金(2015M571414);哈尔滨工业大学(威海)校科学研究基金(HIT(WH)201411)资助课题

收稿日期：2014-08-15；修回日期：2014-10-29；网络优先出版日期：2014-12-29。