股票投资模型中的一个强偏差定理

胡光军，程　成

(安徽工业大学 数理科学与工程学院，安徽 马鞍山 243002)



股票投资模型中的一个强偏差定理

胡光军，程成

(安徽工业大学 数理科学与工程学院，安徽 马鞍山 243002)

摘要：利用广义似然比以及广义渐进相对对数似然比作投资股票之间相依程度的一种随机性度量和研究随机序列强极限的分析方法，研究股票市场中投资者进行随机决策时，其收益向量的真实分布与其关于边缘分布平均收益率之间的偏差，在适当的条件下给出偏差的上下界。

关键词：Markov不等式；Borel-Cantelli引理；收益率；强偏差定理；投资组合

1952年，马科维茨(H.Markowitz)提出的投资组合理论奠定了金融投资定量化研究的理论基础，成为现代投资理论研究的主要论题和决策管理实践的重要工具。近年来国内外众多学者对此进行了广泛深入地研究，取得了大量研究成果[1-5]。文献[4]和[5]中作者利用鞅方法研究了一类log-最优投资组合的极限性质。本文应用研究随机序列强极限的分析方法[6-7]，并在证明中提出了将Markov不等式和Borel-Cantelli引理等工具应用于强极限定理的一种途径。

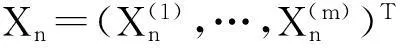
定义设收益向量序列Xan+1,…,Xan+n的联合分布密度函数(或概率函数)为pn(xan+1,…,xan+n)，其边缘分布密度(或分布函数)pk(xk)，k=an+1,…,an+n。称

为广义似然比，并称

为广义渐进相对对数似然比。

定理设{Xn,n≥1}如前定义，c≥0为实常数，{an,n≥1}是非负整数列。令

D∶={ω∶r(ω)<+∞}

如果

c<∞

则

(1)

(2)

其中

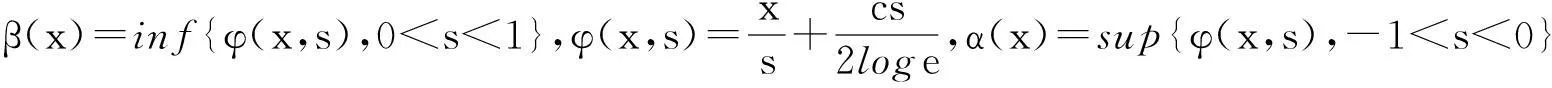
证明设|s|<1，定义：

现定义随机变量如下

注意到

由Markov不等式，对∀ε>0，有

所以

由此，存在A(s)∈F，且P(A(s))=1，由ε的任意性及B-C引理知：

也即

由上极限性质及不等式logx≤(x-1)loge(x>0)，当ω∈A(s)∩D，有

(3)

由(3)及不等式

有

(4)

取0

(5)

设Q*是区间(0,1)中的一个可数稠密子集。令A*=Is∈Q*A(s)，则P(A*)=1，由(5)有

φ(r(ω),s),ω∈A*∩D

(6)

根据φ(r(ω),s)关于s的连续性易知，对每个ω∈A*∩D，存在λn(ω)∈Q*，n=1,2,…,使得

(7)

由(6)和(7)有

β(r(ω)),ω∈A*∩D

(8)

因为P(A*)=1，由(8)即得(1)。

取-1

α(r(ω)),a.s.ω∈D

定理得证。

推论在定理的条件下，若r(ω)=0a.s.或c=0，则

a.s.ω∈D

参考文献:

[1] Markowitz H.Portfolio Selection[J].Journal of Finance，1952,77-91.

[2] 张卫国. 现代投资组合理论-模型、方法与应用[M].北京：科学出版社，1998.

[3] 叶中行，林建忠. 数理经融-资产定价与金融决策[M].北京：科学出版社，2007.

[4] 包振华，叶中行，杨卫国. Log-最优投资组合的极限定理[J]. 数学杂志，2007,27(4)：467-470.

[5] 汪忠志，宋静. 股票投资模型中的一个强偏差定理[J]. 安徽工业大学学报，2008.

[6] Wang zhongzhi.Random transforms for arbitary stochastic sequence and a.s.convergence[J].Journal of Mathematics,2005,25(5):513-520.

[7] 刘文，陈志刚. 对数似然比与离散随机变量序列强极限定理的一种分析方法[J].应用数学学报，1996,19(3):359-368.

On the Strong Deviation Theorems in the Stock Market Model

HU Guang-jun, CHENG Cheng

(School of Mathematics & Physics，Anhui University of Technology，Anhui Ma′anshan 243002，China)

Abstract:In this paper, by using the generalized likelihood ratio and generalized asymptotic relative logarithmic likelihood as a random measure of the dependent degree among the invest in stocks and the analytical methods of studying strong law of limit theorem, the strong deviation between the real distributions of the return rate and the average of their marginal distributions are studied, meanwhile, under suitable conditions, the upper and lower bounds are also obtained.

Key words:Markov's Inequality, Borel-Cantelli Lemma, strong deviation theorems, investment portfolio, rate of return

中图分类号：O211.4，O236

文献标识码：A

文章编号：1007-4260(2015)01-0020-03

DOI：10.13757/j.cnki.cn34-1150/n.2015.01.006

作者简介：胡光军，男，安徽六安人，安徽工业大学数理科学与工程学院硕士研究生， 研究方向为概率论及其应用。

基金项目：安徽省高等学校自然科学基金(1408085MA04)，安徽工业大学研究生创新基金(No.2013090)。

收稿日期：2014-05-05