绝缘薄圆盘和接地导体球间静电放电研究*
李学文,孟 鹤
(1 中国石油化工股份有限公司青岛安全工程研究院,
山东青岛 266071;2 上海海事大学基础实验中心,上海 201306)
绝缘薄圆盘和接地导体球间静电放电研究*
李学文1,2,孟鹤1
(1 中国石油化工股份有限公司青岛安全工程研究院,
山东青岛 266071;2 上海海事大学基础实验中心,上海 201306)
摘要:工业生产过程中,绝缘体静电放电导致燃爆事故,造成严重的人员伤亡及财产损失。该文提出绝缘薄圆盘和接地导体球间静电放电的物理新模型,定量分析球板间静电放电参数。研究结果表明:在一定的球板电极结构下,发生球板静电放电的盘面临界电荷密度δ′≤0.32,圆盘半径越大,临界电荷密度值越小,导体球半径小时,击穿电压值较低,容易发生静电放电。球板间隙发生静电最小放电能量达到0.0475mJ~0.575mJ,放电能量可能引燃H2和空气混合气体,造成燃爆事故。
关键词:静电放电,绝缘圆盘,接地导体球
1引言
绝缘体在工业领域广泛使用,如塑料燃料箱、埋地塑料管线、包装材料等,在易燃、易爆介质(如H2和空气混合气体)场合,绝缘体静电放电导致燃爆事故,造成企业重大损失。目前,绝缘体静电放电研究得到广泛关注。
早在1967年,Heidelberg发现在绝缘体下端有导电金属薄膜时,会产生刷形放电[1]。G.P. Ackroyd对绝缘体刷形放电引起的点火风险进行研究[2]。L. Mueller通过试验方法研究绝缘的静电放电并指出:当绝缘体电荷密度较高时,绝缘体放电形式从刷形放电转化为表面放电[3]。Harold利用球板静电放电结构,通过试验方法测试带电绝缘盘向接地导体球迁移的电荷量,理论分析静电放电条件[4]。
这些研究主要通过试验方法研究绝缘材料整体的静电特性,传播刷形放电的条件,理论分析绝缘体静电放电条件、绝缘体静电放电释放的能量等问题的研究文献不多,绝缘体静电放电是目前静电研究的一个热点和难点。在一定条件下绝缘体同样产生静电放电,只不过放电条件比导体放电苛刻,能量小。绝缘体静电放电能否发生与接地导体的形状、电场分布、介质、绝缘体电荷密度及厚度等因素有关。
本文选择的绝缘体是聚四氟乙烯(简称PVC),PVC具有阻燃及良好电气绝缘性能。研究一个接地导体球和无金属敷层的PVC带电薄圆盘组成的静电放电结构,建立球板静电放电新的物理模型,理论分析导体球场强分布,根据Pederson击穿标准计算球板静电放电的击穿电压、PVC盘临界电荷密度。理论计算带电PVC薄圆盘刷形放电静电能,计算结果与试验数据相吻合。
2球板静电放电物理新模型
图1所示为建立的球板静电放电物理新模型(球板间隙为空气),假设PVC薄圆盘电荷密度均匀分布且δs>0,把PVC带电薄圆盘分隔成N块带电小区域,每个区域等效半径为ref,球板电极结构给定,盘面电荷密度达到临界值时,盘面一个或几个带电区域可能同时发生静电放电。
球板静电放电结构中,半径为a的导体球接地,其球心位于半径为R的PVC薄圆盘中心上方,薄圆盘厚度为dz(4mm~8mm)。PVC薄圆盘和球心分离距离为d,球板间间隙距离为g,盘面电荷密度为δs,接地球点在无穷远处。导体球半径a的范围:10mm~60mm,球板分离距离d的范围:20mm~100mm。以下分析球板间电场分布。
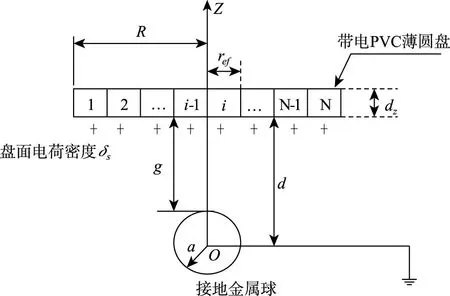
图1 球板静电放电物理新模型
2.1 球-板静电放电间隙场强分布
PVC圆盘以oz轴为中心,导体球也一样,研究球板间沿oz轴z向电场分量。根据文献[5],轴向电场分量Ez′(z′)的解析式为:
(1)
公式(1)中,Ez′(z′)为球板间沿z轴的电场分量,δs′为PVC薄圆盘的面电荷密度,R′为PVC薄圆盘的半径,z′为oz轴上一点坐标,d′为导体球与PVC盘分离距离。公式(1)中各物理量Ez′、δs′、R′、z′、d′均无量纲并定义如下:

考虑PVC盘的电荷密度均匀分布(δs′>0为常数),根据公式(1)计算球板轴向电场的分布规律如图2所示,图2(a)中,导体球半径a=10mm和球板分离距离d=50mm,盘面取不同半径,球板间场强值随盘的半径增大而显著增大,靠近球面场强值最大。图2(b)中,盘的半径R=40mm,球板间隙距离g=30mm,不同球半径下,球板间隙电场分布,从图2(b)可知,导体球半径越小时,球面的场强值越大。

(a)PVC盘不同半径下球板轴向电场分布(b)不同球半径下球板轴向电场分布
2.2 球板静电放电结构的临界场强和击穿电压
从图2球板电极间隙电场分布可知,导体球表面场强值最大,当导体球表面场强值达到临界击穿场强时,静电放电从球面附近开始向PVC薄盘方向发展,球面附近空气发生电离并形成电子崩,在球板电场作用下,电子崩不断发展到PVC薄盘,形成一个放电通道,整个球板间隙被击穿,盘面的分隔小区域的电荷通过放电通道向导体球释放掉(见图1)。本文研究不涉及球板静电放电的电子崩发展,主要研究绝缘体发生静电放电的临界条件及参数。
工程上常采用经验公式Pederson击穿标准研究不同电极结构气体击穿,根据Pederson击穿标准[6]:
(2)
公式(2)中:g为球板空气间隙长度,p为气压(p=1bar),B=2.42kV(mm bar)-1,C=2.08kV(mm bar)-0.5,ξ为导体球表面曲率系数,f(z)为球电极的电场分布函数。
为求解方程(2),必须获取曲率系数ξ和球电极电场分布函数f(z),以下对球电极的曲率系数ξ和电场分布函数f(z)进行分析。根据文献[6],导体球表面临界击穿场强E0取决于电极表面的平均曲率H0,E0与ξ的关系为:
ξ=E0/(pB)
(3)
曲率系数ξ与球板间隙距离g关系满足条件:
ξf(g)=1
(4)
对于球电极的场分布函数为[7]:
(5)
公式(5)中:H0是导体球表面的平均曲率。把方程(5)代入方程(2)并结合公式(4),可以得到下式:
(6)
根据方程(3)、(6),推导出球电极表面起始场强E0与球半径a的关系为:
(7)
公式(7)中:p为气压(p=1bar),B=2.42kV(mm bar)-1。
表1中,Ea的击穿场强是根据本文提出公式(7)计算得到,Eb为文献[4]中参考数据,这两组数据非常吻合。当导体球半径足够大,其临界击穿场强E0=2.42kV/mm,趋于一个常数。考虑到空气的击穿场强值范围为2.1kV/mm~3.0kV/mm,导体球表面的起始场强值均大于空气的击穿场强,空气静电放电能够从球表面发生。导体球半径越小,球表面起始场强值越大,其表面就容易发生放电。

表1 导体球表面起始场强与球半径关系
文献[7]给出球板的击穿电压Vb为:
Vb=ηξB(pg)
(8)
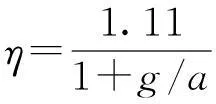
根据公式(8)计算出球板间隙的击穿电压与间隙距离的关系如图3所示(PVC盘半径R=40mm),从图3可知,盘面半径、球板间隙距离相同时,导体球半径越小,间隙击穿电压值越低。这说明满足临界电荷密度的PVC薄盘对小半径的接地导体球更容易被击穿。
吃过之后,我从胡同里往前走,先是有几个妇女问我要不要小姐,后来又有几个妇女悄悄地问我,卖不卖器官。我感到有说不出的恐惧,这时候,有两个青年过来,要勒住我的胳膊,他们要绑架我,你们要干什么?我大喝一声,飞起一脚将一个人踢倒。又一拳将另一个人打倒,我飞快地跑出胡同。

图3 球板电极的击穿电压与间隙距离关系
2.3 球板静电放电结构的临界电荷密度
PVC盘面的临界电荷密度保证导体球表面感应电荷产生场强满足Pederson 击穿标准,同时PVC盘面的电荷密度受到空气击穿场强限制,如果盘面电荷密度太高可能导致表面放电,满足该限制条件下的最大电荷面密度为[4]:
δmax=ε0εrEair
(9)
公式(9)中,真空的介电常数ε0=8.854×10-12F/m,考虑盘面有利放电情况,取圆盘材料相对介电常数εr=1.45(稍小于PVC的介电常数),空气击穿场强Eair=2.1kV/mm,计算出δmax=27μC/m2。
文献[4]给出导体球表面特征电荷面密度为:
δ*=2ε0εrEb
(10)
公式(10)中,Eb为球表面的临界击穿场强,考虑球面的击穿场强随着半径增大而减小,取较小小半径下,Eb(a=10mm)=4.53kV/mm,导体表面εr=1.0,根据公式(10)计算可得δ*=83μC/m2。为求解PVC盘的临界电荷密度,在公式(1)中,球表面(z′=1)且满足击穿条件:Ez′=1,可以得到PVC盘上的临界击穿电荷密度δ′为:

(11)
根据公式(11)并考虑盘面临界电荷密度限制条件,PVC盘临界电荷密度与球板间隙距离关系见图4。从图4可知,当R′=0.32、1.0时,盘电荷密度大于0.32(盘面最大电荷密度),所有这两种情况下,球板间不会发生静电放电;当R′=3.16时,球板间隙g′≤2.5时,满足条件δ′≤0.32,可以发生静电放电,当g′在区间[2.5,5]时,δ′>0.32,球板不会发生静电放电。当R′=6时,对整个球板间隙均满足临界电荷密度限制条件,所有这种情况球板是会发生静电放电。这说明PVC盘即满足临界电荷密度条件,球板电极结构能否放电还受到盘面半径的制约,盘面半径不能太小。

图4 PVC盘临界电荷密度与球板间隙距离关系
PVC盘在满足临界电荷密度限制条件下,盘的半径和球板间隙的距离之间存在一定函数关系,以下进行推导。在公式(11)中,令D=d′-1,可以推导出如下公式:
(12)
(13)
如果盘面临界电荷密度δ′值分别取0.1、0.15、0.2、0.32,球板间隙距离g′范围[1,5],根据公式(12)、(13)计算盘面不同临界电荷密度下,盘的半径和球板间隙距离必须满足的条件(见图5)。从图5可知,盘面临界电荷密度满足δ′≤0.32时,盘面半径必须大于最小半径,例如δ′=0.15,盘面半径R′≥5.0。球板间隙分离距离d′相同时,临界电荷密度δ′越大,盘面半径越小。

图5 不同临界电荷密度下PVC盘半径R′与球板
3静电放电能量的计算
图6所示为球板新物理模型下,PVC带电薄圆盘被分隔成N块带电小区域。球板电极结构静电放电发生从球表面开始,空气电离形成电子崩向PVC盘方向发展形成主放电通道,当放电主通道发展到盘面时,N块带电小区域中的一块或若干块同时发生放电,形成分枝并汇集到放电主通道中,整个间隙击穿。整个球板静电放电能量就是各块带电小区域静电能之和,由于无法确定盘面带电区域同时放电数目,所以精确计算球板静电放电能量很困难。

图6 带电薄圆盘分隔成N个小的区域
考虑极端情况,盘面仅有一块小区域发生静电放电,很容易计算出该带电小区域静电放电能量。PVC盘面的静电放电是局部放电现象,仅将一部分能量释放出来。球板静电放电过程中的最小静电能Wmin可以表示为:
(14)
公式(14)中,V为盘面电压,δs为盘面临界电荷密度,s为带电小区域面积。文献给出绝缘盘表面电压为:
V=δsdz/ε0εr
(15)
公式(15)中,dz为盘的厚度。HAROLD在研究带电绝缘盘刷形放电时[4],提出等效放电半径ref的概念,给出球板电极静电小区域放电转移电荷量ΔQ为:
(16)
公式(16)中,K为常数1,d为球板分离距离。根据公式(15)、(16)可以推导出球板静电放电能为:
(17)
为计算球板释放最小静电能范围,选取参数盘面临界电荷密度取δs=27μC/m2,盘的相对介电常数取εr=1.43给定,当盘面厚度dz取4mm或8mm,球板分离距离d取20mm或100mm,根据公式(17)计算球板最小静电能如表2所示。

表2 球板最小静电能Wmin
考虑球板间隙为H2与空气混合气体时,H2的最小点火能仅有0.19mJ。从表2可知,球板分离距离为30mm,盘厚度为8mm,球板最小静电能为0.207mJ>0.19mJ。球板分离距离达到50mm,盘的厚度为4mm或8mm时,球板最小静电能均大于0.19mJ。
4结论
在建立球板静电放电物理新模型基础上,依据球板间基本电场分布公式及Pederson击穿标准,理论分析PVC盘临界电荷密度、球板间的击穿场强及击穿电压,理论计算球板静电放电的最小静电能,得到如下结论:
(1)球板静电放电结构发生静电放电,PVC盘面电荷密度δ′须达到临界值且满足条件:δ′≤0.32,盘面的半径R′必须大于最小半径值,临界电荷密度值越大,PVC盘的半径越小(见图5)。
(2)根据Pederson击穿标准,导体球表面临界击穿场强由球半径a决定,球板击穿电压主要由球板间隙距离g′及球球半径决定。对于小半径导体球、大半径PVC盘的球板结构,盘面临界电荷密度小,球板间隙击穿电压低,这种情况下,球板静电放电容易发生。
(3)球板静电放电最小静电能与球板分离距离、球板间介质、PVC盘的临界电荷密度及厚度有关。本文研究球板电极结构下,球板静电放电能的范围:0.047mJ~0.575mJ。这对于有H2及空气混合气体场合,PVC盘对导体球的静电放电能可能超过H2最小点火能0.19mJ,导致燃爆事故。
参考文献
[1] J.L. Davidson. Electrostatic discharges between charged insulators and grounded spheres[J]. Journal of Electrostatics,2002,56:29-42.
[2] G.P. Ackroyd,S.G. Newton. An investigation of the electrostatic ignition risks associated with a plastic coated metal[J]. Journal of Electrostatics,2003,59:143-151.
[3] L. Müller,K.Feser. Experimental investigation of discharges for charged plastic or plastic-coated materials. CEIDP 2001,Kitchener,Canada. A.J.Medlin. A pseudotransient approach to steady state solution of electric field-space charge coupled problems[J]. J.Electrostatics,1998,43:39-60.
[4] Harold L. Induced-charge errors in charge-transfer measurement:Brush discharges between charged,insulating discs and earthed,conductive spheres[J]. Journal of Electrostatics,2010,68:5-20.
[5] Kenneth L. Kaiser. Electrostatic Discharge[M]. Published in 2006 by CRC Press Taylor & Francis Group.
[6] A. Pedersen. On the Electrical Breakdown of Gaseous Dielectrics An Engineering Approach. IEEE Transactions on Electrical Insulation Vol.24 No.5,October 1988.
[7] 丘毓昌. GIS装置及其绝缘技术[M].水利电力出版社.

*基金项目: 中石化青岛安全工程研究院化学品安全控制国家重点实验室开放基金项目(No:10010104-15-ZC0609-0004)
Research on Electrostatic Discharge Between Insulating
Thin Disc and a Grounded Sphere
LI Xue-wen,MENG He
(1 State Key Laboratory of Chemicals Safety,Qingdao Safety Engineering Institute,SINOPEC,Qingdao 266071,Shandong,China;2 Experiment center of basic course,Shanghai Maritime University,Shanghai 201306,China)
Abstract:Industrial processes are extremely sensitive to electrostatic hazards and the consequences of the events can be very severe,leading to huge financial loss and possible human injury. This paper builds a physical model of ESD(electrostatic discharge)between a thin insulation disc and a grounded metal sphere. Quantitative analysis has been made about discharge parameters of ESD. Under the structure of sphere-plate,critical disc charge density satisfies the condition δs′≤0.32 if ESD occurring. The bigger radius is,the smaller critical charge density is. When radius of sphere being smaller,the value of breakdown voltage being lower,so it is easy to discharge. The results showed that the minimal electrostatic discharge energy ranging from 0.047mJ to 0.575mJ,minimal energy of discharge can possibly ignite the hydrogen mixtures and lead to electrostatic hazards.
Key words:electrostatic discharge,insulating disc,grounded sphere
中图分类号:O 53

