扇贝闭壳肌薄层干燥的数学模型

俞微微，刘俊荣，沈建，丛海花

(1.大连海洋大学 食品科学与工程学院，辽宁 大连 116023； 2.中国水产科学研究院渔业机械仪器研究所 农业部渔业装备与工程重点开放实验室，上海 200092)



扇贝闭壳肌薄层干燥的数学模型

俞微微1，刘俊荣1，沈建2，丛海花1

(1.大连海洋大学 食品科学与工程学院，辽宁 大连 116023； 2.中国水产科学研究院渔业机械仪器研究所 农业部渔业装备与工程重点开放实验室，上海 200092)

摘要:以栉孔扇贝Chlamys farreri闭壳肌为研究对象，对其热风干燥特性进行了研究。将扇贝样品经处理后于45、55、 65、75 ℃ 温度下进行热风干燥，监测样品的质量变化，所采取的监测频率为干燥开始的第1小时监测4次，第2小时监测2次，第 3小时后每小时监测1次，所有的干燥过程都处于降速阶段，并用薄层干燥模型对测量结果进行处理，选用Henderson-Pabis、Wang and Singh、Diamante et al.、Page、Newton 5种数学模型进行拟合，通过计算相关系数(R)、决定系数(R2)、平均偏差(eave)、卡方检验(2)、均方根误差(RMSE )、相对平均偏差(P)的大小，来检验拟合程度。结果表明：在45、55、65、75 ℃ 干燥温度下,Henderson-Pabis、Diamante et al.、Page、Newton 4个模型有效；进一步分析4个模型中模型常数随温度的变化，发现其中Henderson-Pabis、Page、Newton 3个模型参数中含有干燥温度为变量的通式模型，可以有效地预测干燥温度在45~75 ℃时的干燥进程，3个通式模型依次为MRH=0.9673exp[-(7×10-5T-0.0009)]t、MRP=exp(-0.00323t0.0039T+0.7727)和MRN=exp[-(7×10-5T-0.0008)]t。

关键词:扇贝闭壳肌；薄层干燥；数学模型

扇贝闭壳肌的传统干燥方法是用日光干燥，国内已有一些学者对扇贝闭壳肌的一些干燥方法进行了研究[1-6]，主要有热风干燥和微波真空干燥。热风干燥因其具有设备投资少、适应性强、操作控制简单等特点，已被广泛应用于水产品干燥。干燥技术的发展既需要工业实践，也需要学术研究，人们一直希望通过干燥理论的研究建立干燥模型，以期在计算机控制上取得最佳结果，为生产实践带来变革[7]。

干燥的计算机模拟，关键是干燥数学模型，而薄层干燥数学模型是基础。国外对热风干燥数学模拟的研究起步较早，国内的研究始于20世纪80年代，开始是针对粮食，现在已发展到蔬菜、水果和一些水产品[8-18]，但对扇贝闭壳肌热风干燥数学模型的研究目前尚未见报道。

本研究中，通过进行栉孔扇贝Chlamysfarreri闭壳肌的热风干燥试验，建立扇贝闭壳肌薄层干燥数学模型，为热风干燥技术在干贝生产中的应用和生产控制提供理论依据。

1材料与方法

1.1材料

试验用栉孔扇贝购于大连市桃源街农贸市场。

1.2方法

1.2.1样品的预处理将鲜活扇贝洗净后投入沸水中，待贝壳张开后立即取出并冷却，然后割下扇贝闭壳肌，去膜漂洗。将漂洗干净的扇贝闭壳肌再放入100 ℃、8%盐水中煮1 min，捞出沥干[6]，取样测定初始水分。扇贝闭壳肌的初始湿基水分为75%左右，规格约300粒/kg。

1.2.2干燥试验将预处理后的扇贝闭壳肌以单层形式放于金属网帘上，分别在45、55、65、75 ℃热风温度下进行干燥试验，热风风速为1.5 m/s，每一温度下设3个重复试验，结果取其平均值。

水分变化是通过干燥过程中样品的质量变化来获得，干燥开始的第1个小时，每隔15 mim测量1次，干燥的第2个小时，每隔30 min测量一次，干燥2 h后每隔60 min测量一次，试验持续时间为8~10 h。湿基水分按下式计算：

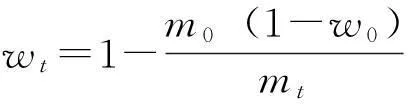
(1)

其中：m0为物料的初始质量(kg)；mt为t时刻物料的质量(kg)；w0为物料的初始水分(湿基)；wt为t时刻物料的水分(湿基)。

1.2.3干燥数据的处理干燥研究中，通常用水分比随时间的变化来研究物料的干燥过程，水分比(MR)定义如下：

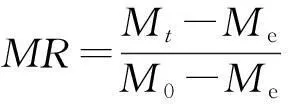
(2)

其中：Mt为t时刻物料的水分(干基)；M0为物料的初始水分(干基)；Me为物料的平衡水分(干基)。

在热风干燥中，由于平衡水分Me相比于M0和Mt要小得多，因此，水分比的计算可采用以下的简化公式[17]：

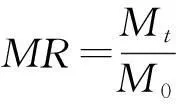
(3)

干燥速率按下式计算[18]：

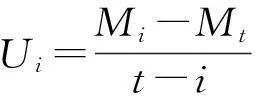
(4)

其中：Ui为i时刻样品的干燥速率(min-1)；Mi为i时刻样品的干基水分。

1.2.4数学模型从目前常见的用于描述物料薄层干燥的数学模型中选5种用于本研究，结果如表1所示。

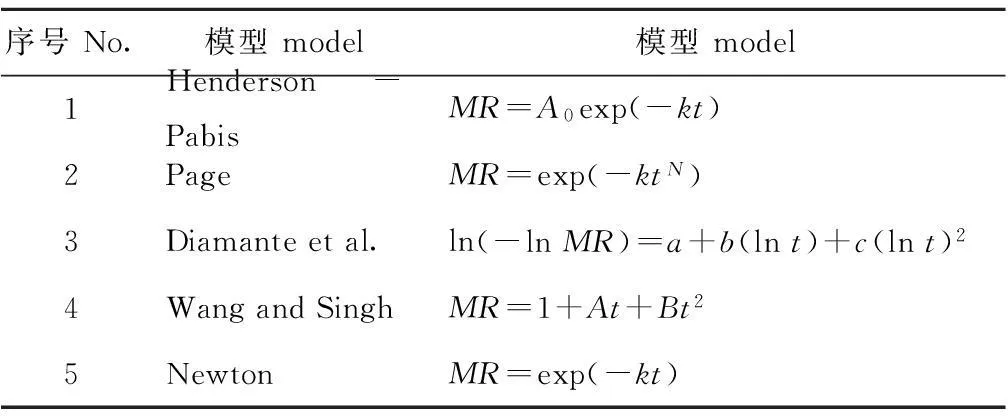
表1　薄层干燥的数学模型

注：模型中t为干燥时间,A0、k、N、a、b、c、A、B为待定常数

Note:tis drying time in the models,A0,k,N,a,b,c,A andBare constants in the models

用Excel 软件对试验数据进行曲线拟合处理，非线性回归分析用于5个模型中常数的估计。用相关系数(R)、决定系数(R2)、平均偏差(eave)、卡方检验(2)、均方根误差(RMSE)和相对平均偏差(P)来检验模型预测值与实测值的拟合程度。其计算公式[17]为

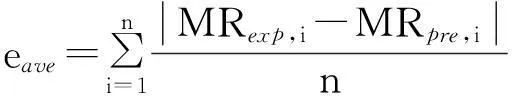
(5)

(6)

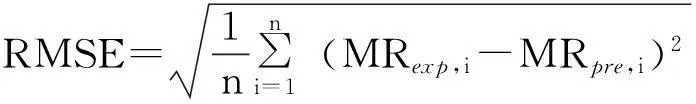
(7)

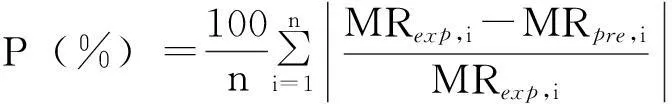
(8)

其中：MRexp,i为试验观测值；MRpre,i为模型预测值；n为试验观测值个数；z为模型中参数个数。eave、2、RMSE越接近零，预测值与实测值越接近，表明拟合效果越好。

2结果与分析

2.1温度对水分比和干燥速率的影响

不同温度下，扇贝闭壳肌干燥过程中的水分比变化见图1，干燥速率随时间的变化见图2。

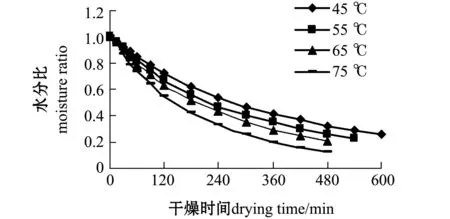
图1　热风温度对水分比的影响Tab.1　Effect of drying temperatures on moisture ratio

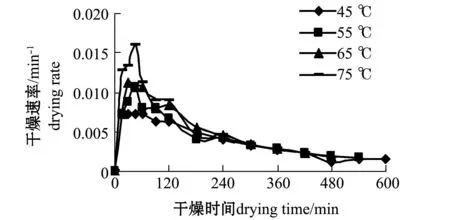
图2　热风温度对干燥速率的影响Tab.2　Effect of drying temperatures on drying rate

从图1可见，在干燥开始阶段，水分比降低比较快，一段时间后，水分比降低速度减慢，且温度越高，水分比下降越快。

从图2可见，在干燥开始阶段，干燥速率迅速达到最大，然后干燥速度逐渐下降，整个干燥过程基本处于降速阶段，无明显的恒速干燥过程。在干燥初始阶段，热风温度对干燥速率的影响较大，温度越高，干燥速率越高，随着干燥时间的延长，不同温度的干燥速率差异越来越小，3 h后，趋于一致，这与Purkayastha 等[17]对西红柿片的薄层干燥和关志强等[18]对荔枝果肉热风干燥薄层模型的研究结果相似。说明扇贝闭壳肌热风干燥基本是内部水分扩散控制的降速干燥过程。

2.2不同干燥温度下薄层干燥模型参数的确定

通过曲线拟合，得到4个干燥温度下扇贝闭壳肌热风干燥的5种模型中待定参数见表2，拟合度检验的统计分析见表3。

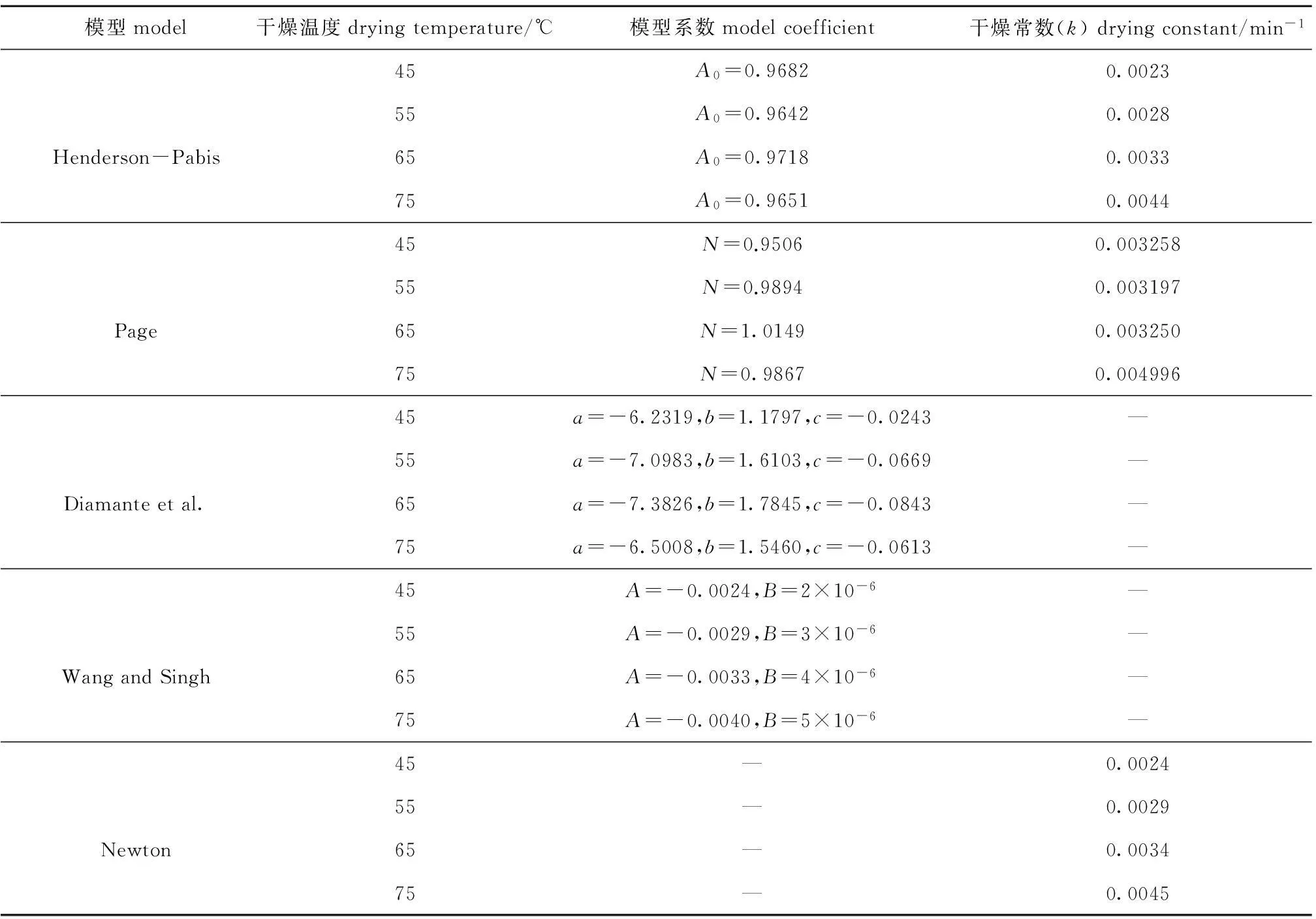
表2　不同温度下5种模型中的待定参数

从表3可见：5种模型在4个干燥温度下，相关系数R均大于0.995，表示拟合程度较高；eave、2、RMSE均比较小，预测值与实测值的相对平均偏差P除Wang and Singh 模型的较大外，其余4种模型的P值均未超过4%，说明Henderson-Pabis、Page、Diamante et al.、 Newton 4种模型都能很好地描述4个干燥温度下扇贝闭壳肌干燥过程中水分比随时间的变化规律。

2.3一定干燥温度范围内薄层干燥通式模型参数的确定

进一步分析4种模型中的参数发现，在实验选定的温度范围内，Henderson-Pabis模型中的A0和Page模型中的k随温度变化较小，Henderson-Pabis模型和Newton模型中的k值及Page模型中的N值与温度近似呈线性关系，可得干燥温度在45~75 ℃时的3种通式模型，而Diamante et al.模型中的参数a、b、c随温度的变化比较复杂，不呈现某种规律性，无法找出通式。通过对数据分析，得出温度在45~75 ℃时，扇贝闭壳肌薄层干燥通式模型如下：

① Henderson-Pabis模型

MRH=0.9673exp[-(7×10-5T-0.0009)]t；

② Newton模型

MRN=exp[-(7×10-5T-0.0008)]t；

③ Page模型

MRP=exp(-0.00323t0.0039T+0.7727)。

上述模型中的T为温度(℃)，t为干燥时间(min)。

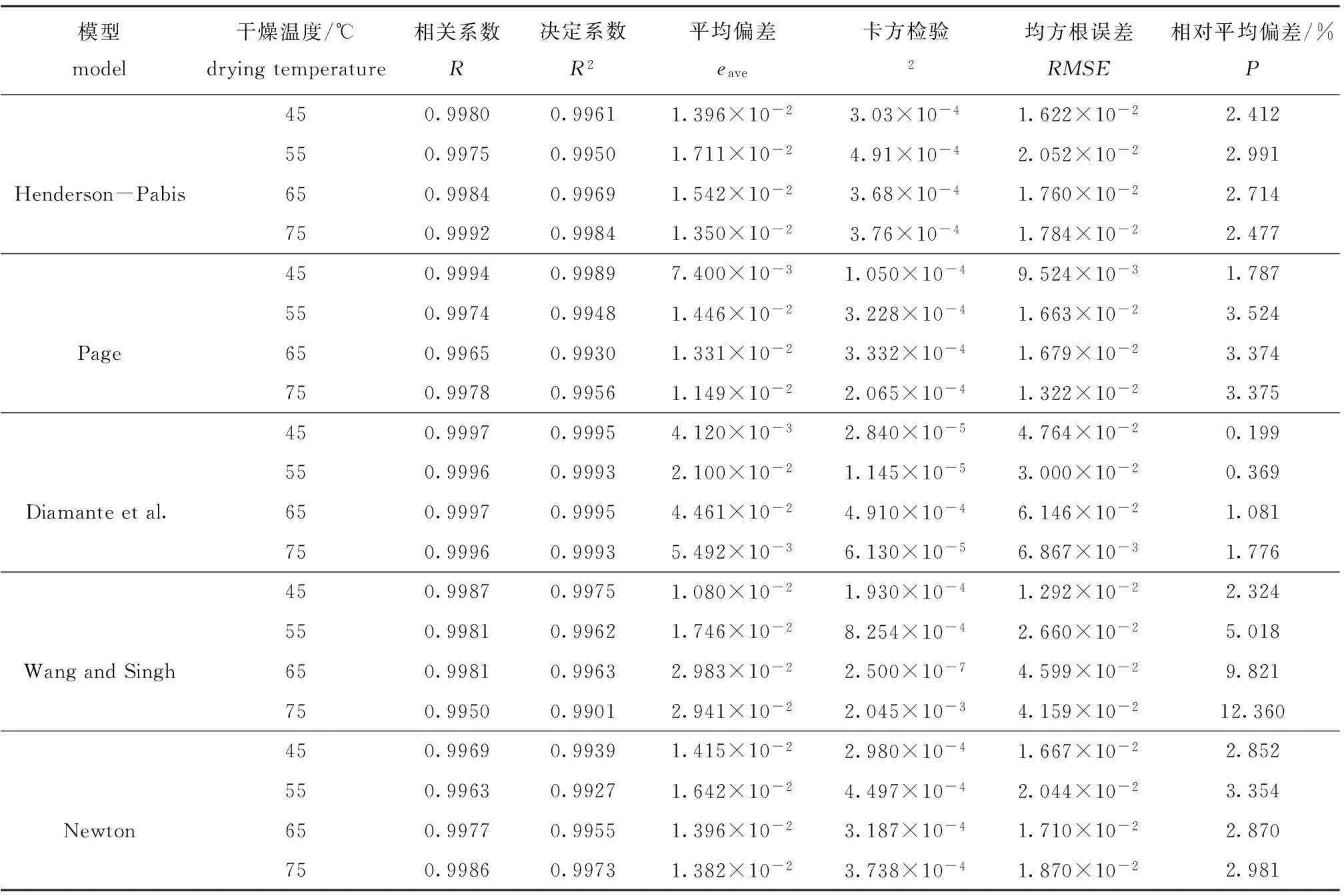
表3　5种模型预测值与实测值拟合程度的统计分析

3种模型的预测值与实验测试值拟合程度的统计分析见表4。从表4可见，eave、2、RMSE都比较小，预测值与实测值的相对平均偏差P均不超过6.5%，说明3种通式模型在45、55、65、75 ℃时的预测值与实测值一致性较好，在该干燥温度范围内，扇贝闭壳肌干燥过程中水分比随时间的变化可方便地选用此3种通式模型中任何一种来预测。

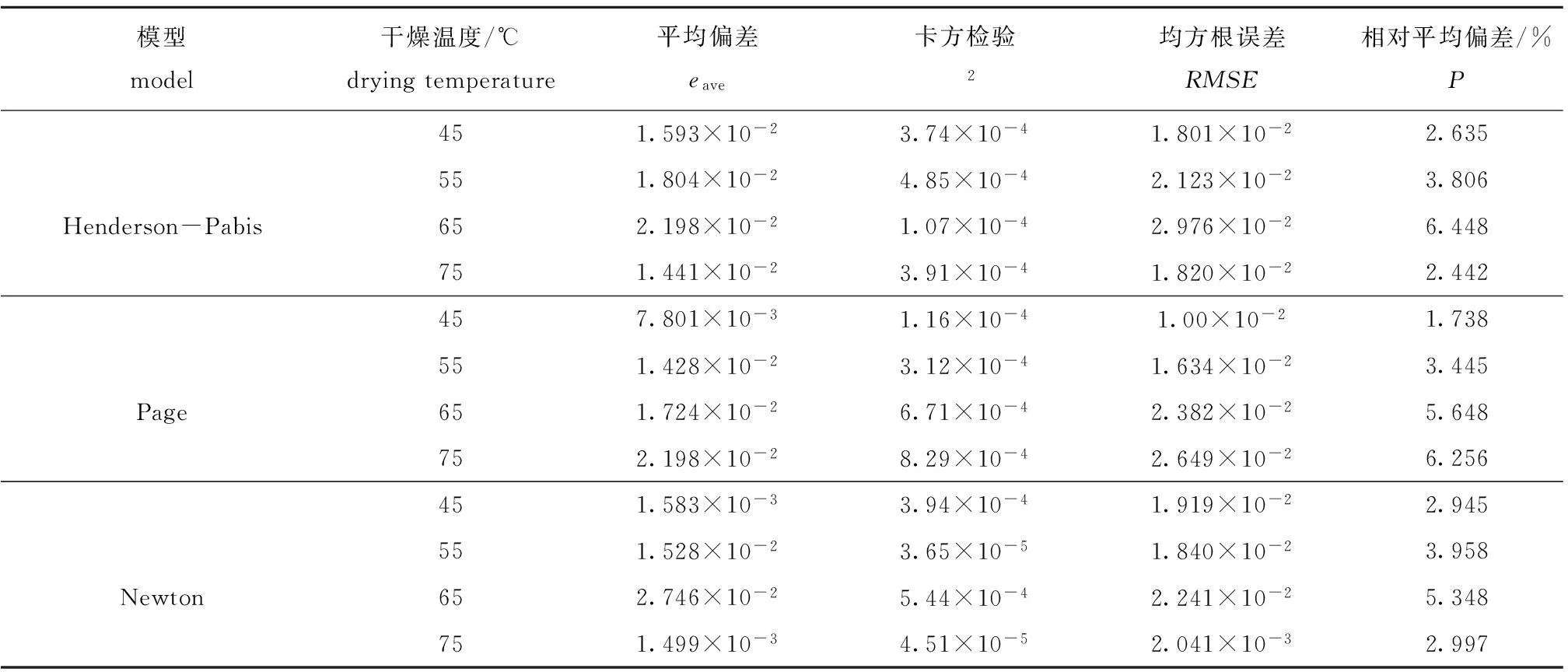
表4　3种模型预测值与实测值拟合程度的统计分析

3结论

本研究表明，扇贝闭壳肌在45、 55、65、75 ℃ 4个干燥温度下，其干燥过程基本属于内部水分扩散控制的降速干燥过程，干燥过程中水分比随时间的变化可采用Henderson-Pabis、Page、Diamante et al.、 Newton 4种模型中任一种来预测。进一步地，在45~75 ℃范围内的任一温度下，干燥过程中扇贝闭壳肌水分比随时间的变化可选用参数中含有以干燥温度为变量的Henderson-Pabis、Newton、Page 3个通式模型中的任意一个来预测干燥进程。

参考文献：

[1]张倩,张国琛,母刚，等.微波真空干燥对虾夷扇贝闭壳肌营养成分的影响[J].大连海洋大学学报,2013,28(6):604-609.

[2]张国琛,牟晨晓,潘澜澜,等.热风干燥参数对扇贝柱干燥速度及品质的影响[J].大连水产学院学报,2004,19(1):35-39.

[3]张国琛,毛志怀,牟晨晓,等.微波真空干燥扇贝柱的物理和感官特性研究[J].农业工程学报,2004,20(3):141-144.

[4]张国琛,毛志怀,牟晨晓,等.微波真空与热风组合干燥扇贝柱的研究[J].农业工程学报,2005,21(6):144-147.

[5]张国琛,张倩,齐妍,等.变功率微波真空间歇干燥扇贝闭壳肌的研究[J].大连海洋大学学报,2012,27(4):350-354.

[6]刘征,王颉,张政.不同热风干燥温度对扇贝柱干燥特性及品质的影响[J].食品工业,2012,33(8):37-40.

[7]殷丽春,毛志怀.玉米薄层干燥的试验研究[J].农机化研究,2005(1):197-198.

[8]刘正怀.切片食品干燥过程中传热传质的计算机模拟研究[D].杭州:浙江大学,1999.

[9]彭桂兰,吴文福.萝卜丝薄层干燥试验及其数学模型的建立[J].农业机械学报,2005,36(3):79-81.

[10]刘正怀,王俊.切片土豆干燥中传质过程模拟与分析[J].科技通报,2001,17(4):6-10.

[11]李业波,秦玉昌,李业德.土豆干燥过程中内部传热传质的数值模拟[J].农业工程学报,1996,12(3):52-55.

[12]段振华,冯爱国,向东,等.罗非鱼片的热风干燥模型及能耗研究[J].食品科学，2007,28(7)：201-205.

[13]张琼,章梁,黄泽元.草鱼鱼片热风干燥特性的研究[J].武汉工业学院学报，2008,27(4):13-17.

[14]Basavaraj M,Prabhu Kumar G P,Sathyanarayana B R.Determination of drying rate and moisture ratio of fig fruit (FicuscaricaL.) by thin layer hot air drying method[J].J Food Sci Technol,2008,45(1):94-96.

[15]Mudgal V D,Pande V K.Thin layer kinetics of bitter gourd (MimordicacharantiaL.)[J].J Food Sci Technol,2009,46(3):236-239.

[16]Tunde-Akintunde T Y,Afon A A.Modelling of hot-air drying of pretreated cassava chips[J].Agric Eng Int:CIGR Journal,2010,12(2):34-41.

[17] Purkayastha M D,Nath A,Deka B C,et al.Thin layer drying of tomato slices[J].J Food Sci Technol,2013,50(4):642-653.

[18]关志强,王秀芝,李敏,等.荔枝果肉热风干燥薄层模型[J].农机机械学报,2012，43(2)：151-159.

Mathematic models of thin layer drying in scallop adductor

YU Wei-wei1, LIU Jun-rong1, SHEN Jian2, CONG Hai-hua1

(1.College of Food Science and Engineering, Dalian Ocean University, Dalian 116023, China; 2.Key Laboratory of Fishery Equipment and Engineering, Ministry of Agriculture, Fishery Machinery and Instrument Research Institute, Chinese Academy of Fishery Sciences, Shanghai 200092, China)

Abstract：The hot air convective drying characteristics of scallop adductor were investigated. The pretreated samples were dried at 45, 55, 65 and 75 ℃, and weighed in a 15 min interval in the first hour, in a 30 min interval in second hour, and in a 60 min interval thereafter at falling speed. Five thin layer drying models including Henderson-Pabis, Wang and Singh， Diamante et al., Page and Newton were established based on the experimental data for the test model by correlation coefficient(R)，decision coefficient(R2)，average deviation(eave), Chi-square test(2)，root-mean-square error(RMSE) and lelative average deviation(P) in order to screen a suitable drying curve. It was found that four models (Henderson-Pabis, Diamante et al., Page and Newton) were proved to be effective. Furthermore, the effects of temperature on model constants of the four models were analyzed, and the three general models (Henderson-Pabis, Page, and Newton ) including drying temperature as variable were effectively used to predict the drying process effectively in the drying temperature range from 45 ℃ to 75 ℃. The models were expressed as MRH=0.9673exp[-(7×10-5T-0.0009)]t, MRP=exp(-0.00323t0.0039T+0.7727) and MRN=exp[-(7×10-5T-0.0008)]t.

Key words：scallop adductor; thin layer drying; mathematic model

作者简介：俞微微(1961—)， 女， 副教授。E-mail:yww0410@dlou.edu.cn

基金项目：国家现代农业技术产业体系项目(NYCYTX-47)

收稿日期：2014-06-09

中图分类号：TS205.1

文献标志码：A

文章编号：2095-1388(2015)02-0211-05

DOI：10.3969/J.ISSN.2095-1388.2015.02.019