滑模控制在制导弹药弹道跟踪中的应用
杨荣军,叶 瑶,闫德恒,王 寅
(1.中国电子科技集团第二十八研究所,南京 210007;2.南京农业大学 公共管理学院,南京 210095)
滑模控制在制导弹药弹道跟踪中的应用
杨荣军1,叶瑶2,闫德恒1,王寅1
(1.中国电子科技集团第二十八研究所,南京 210007;2.南京农业大学 公共管理学院,南京 210095)
摘要:为使制导弹药有效地沿方案弹道飞行,研究了以姿态角为控制指令的三维滑模弹道跟踪控制系统。探讨了基于弹道修正策略的跟踪控制方案,将动态逆方法与趋近律滑模控制相结合设计了跟踪控制器。分析了控制器参数与系统的闭环稳定性、抖振与跟踪性能之间的关系。根据空间几何运动关系设计了过渡参考弹道,有效避免了启控点偏差带来的控制饱和问题,并给出了光滑的控制指令信息。弹道仿真表明,滑模控制可使制导弹药较严格地按期望轨迹飞行,对各种干扰具有较强的鲁棒性,控制器边界层参数的选择需综合权衡控制精度和抖振问题。
关键词:制导弹药;弹道跟踪;弹道控制;滑模控制;非线性控制
弹道跟踪的核心内容是设计使飞行器沿预设空间轨迹飞行的控制规律。目前的应用主要有:无人机在按规划航迹飞行完成侦察、监视和打击作战任务,制导弹药沿设定的方案弹道实施滑翔增程、中制导,或飞行试验平台模拟特殊弹道环境。弹道跟踪要求在各种干扰情况下尽可能地保证飞行轨迹、速度偏角和姿态角等控制精度。
在制导弹药的实际飞行过程中,不仅各种制造误差、气动误差、风等因素影响其飞行动态,还可能存在启控位置偏差大、气动可用过载小等情况,此时需要采取合适的策略将其引导到方案弹道上。控制系统设计师根据不同原理、弹道参数指令,可以构建不同形式的弹道跟踪规律。早期的方案弹道主要是通过程控来实现,其控制精度受飞行中的干扰影响较大。现在主要采用2种策略:一种是根据位置偏差对实际弹道进行修正,另一种是采用导引规律将对象导向方案弹道上选取的离散航迹点(虚拟目标点)。位置偏差修正方法可实时逼近预定程序的位置指令,体现了对方案弹道的实时动态跟踪过程,而传统的制导方法强调的则是点对点命中。
目前,工程上采用位置偏差修正策略的手段主要是:基于小扰动假设模型,根据飞行弹道与基准弹道的偏差采用线性控制方法。该方法通常对平直方案弹道才能取得较好的跟踪效果[1-2]。对于气动舵面小、无动力飞行等约束的制导弹药,重力的影响不能忽略,对应于水平直飞情况下的模型线性假设也不成立。另外,基于增益调度法的控制系统设计、参数整定与飞行弹道关联紧密,且缺乏稳定性证明,在跟踪机动飞行弹道时表现出各种不足。
针对实际飞控系统存在的建模非线性、耦合和不确定性等问题,一些现代控制方法为提升飞行控制品质提供了解决方案。其中,动态逆方法扮演了重要的角色,然而其应用依赖于精确的数学模型。滑模控制对参数摄动和干扰具有不变性,将动态逆方法与滑模控制结合是一种有效途径。该方法是将研究对象变化为正则形式,然后设计具有鲁棒性能的滑模控制器。Wang将滑模控制与观测器相结合,研究了垂直起降飞行器的高精度控制技术。Lee以角速度分量和推力变化率为输入,建立了飞行器的三维质心控制模型,然后设计了基于滑模理论的弹道跟踪控制系统,并通过仿真验证了存在模型误差情况下该方案的可行性。值得注意的是,滑模控制方法的强鲁棒性能与切换增益项的大小密切相关,增益过大将伴随控制量大、抖振强等现象,应用中需研究切换增益与模型扰动界的关系,从而保证其良好的性能。对于慢变气动参数的不确定问题,引入自适应策略也是一种可参考方案。另外,一般采用气动控制方式的飞行器不能调节轴向速度的大小,难以按时间历程直接跟踪原基准弹道。Bouadi对此引入了一种以距离为独立变量的动态变换方法。
制导弹药在大气中的飞行历程同时存在非线性、时变、耦合和不确定性等特性,这给弹道跟踪控制系统的分析与设计带来了巨大的挑战。本文以气动控制机制的制导弹药为对象,从弹道力学特性和滑模控制原理上着手,探讨弹道跟踪控制器的设计问题。
1弹道修正滑模控制系统设计
1.1方案弹道跟踪控制原理
制导弹药弹道跟踪控制原理如图1所示。弹载计算机根据预设方案弹道指令和实际状态之间的误差,通过质心控制器求解法向加速度,再转换成攻角、侧滑角等指令信号作为姿态回路的输入指令。而姿态控制回路可采用较为成熟的经典控制器或动态逆方法设计,可等效为一个二阶动态环节。姿态角产生作用在制导弹药上的力改变飞行弹道,使制导弹药沿预设方案弹道飞行。由于制导弹药主动段的工作时间短、速度变化剧烈,同时气动舵提供的控制力有限,通常仅在弹道降弧段对飞行轨迹进行调整。
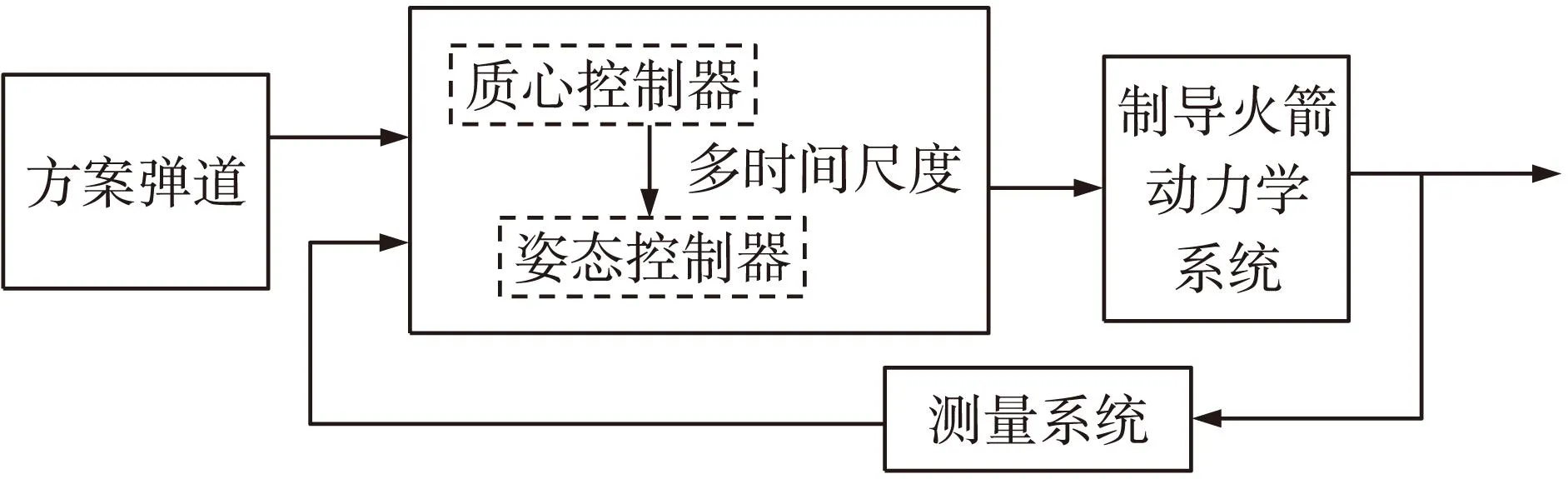
图1 制导弹药弹道跟踪控制原理图
1.2质心环节滑模控制律设计
质心控制律的主要任务是获取使制导弹药跟踪预定质心运动指令(高度yc和侧偏指令zc)的姿态角。选择状态变量X=(yzθψ)T,y,z,θ,ψ分别为高度、侧偏、弹道倾角和弹道偏角;控制变量u=(αβ)T,α,β分别为攻角和侧滑角;参考弹道质心运动输出指令为Yc=(yczc)T,当存在不确定情况时,控制系统可写为
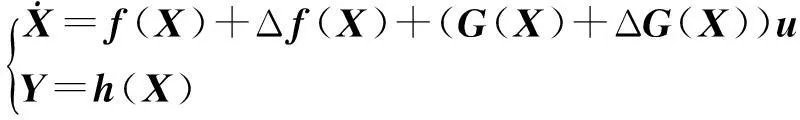
(1)
非线性函数及其不确定项为
f(X)= (f1f2f3f4)T
f1=vsinθ,f2= -vcosθsinψv
f3= -gcosθ/v,f4= 0
Δf(X)=(00ΔFy/(mv)-ΔFz/(mvcosθ))T
控制增益矩阵及其不确定项为
ΔG(X)=G(X)Δav/av
输出方程为
h(X)=(yz)T
式中:ΔFy、ΔFz分别为垂直于速度矢量的纵向力和侧向力的不确定项;v为飞行速度,g为重力加速度,av表示攻角偏量为一个单位引起的速度方向转动角速度增量。
通过非线性坐标变换得到正则形式:
ΔE(X))u
(2)
式中:Lfh,LΔfLfh分别为f和Δf的李导数形式;E(X),ΔE(X)分别为G(X)和ΔG(X)的李导数形式。
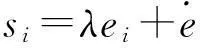
u=-E-1(F+Ks+εsgn(s))
(3)
上式切换增益ε为待定正常数,描述滑模趋近速度对角矩阵为K=diag(k1,k2),符号函数向量定义为sgn(s)=(sgn(s1)sgn(s1))T。
控制律中有关向量和矩阵表达式为
为了使系统状态到达并保持在滑动模态面上,还需确定控制律中的切换增益ε。
1.3闭环系统稳定性分析
令李雅普诺夫函数:
V(X)=sTs/2
(4)
将控制律代入并微分可得:
Ks+εsgn(s))]≤‖s‖‖ΔF‖-sTKs-ε‖s‖+
‖ΔE·E-1‖(‖F‖‖s‖+sTKs+ε‖s‖)≤
-ε(1-‖ΔE·E-1‖)‖s‖+(‖ΔF‖+
‖ΔE·E-1‖‖F‖)‖s‖-sTKs(1-‖ΔE·E-1‖)
(5)
若实际系统模型参数的摄动量有界,且下式成立:
1-‖ΔE·E-1‖>0
(6)
为了保证闭环控制系统在模型扰动的界上仍具备鲁棒性能,容易证明滑模控制器切换增益ε应满足:
(7)
为保证闭环系统的鲁棒性,控制器的切换增益须满足大于等效模型扰动的界。如果姿态控制系统性能较为理想,那么该质心控制律可以保证制导弹药在气动参数不准确的情况下也能到达并保持在滑动模态,实现对预定滑翔弹道高度、侧偏指令的跟踪。
1.4控制抖振与跟踪性能分析
综合误差si的界可以直接转换为飞行状态误差的界限。如ei(0)=0,eε=φ/λ(φ为边界层厚度),则有:
(8)
在边界层内平滑控制的抖振本质上是通过一个低通滤波器结构来实现的。设系统干扰项为ΔFi,将符号函数修改为饱和函数,则边界层内的系统运动为
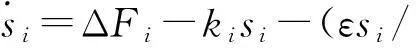
(9)
直观的意义是,干扰通过滤波器被过滤掉得到连续的动态si,而si再通过低通滤波转换过来得到最终的跟踪误差,于是在边界层内可以消除抖振。
若控制使系统状态收敛到边界层区域内,则稳态跟踪误差ei≤eε。根据该特性,可通过调整控制律中的切换增益、边界层参数以达到跟踪精度和鲁棒性能之间的某种权衡。
2过渡参考弹道设计
当启控点偏差较大时,直接对原方案弹道跟踪会造成气流姿态角饱和,飞行控制过程中的诱导阻力将使速度急剧损失。这里考虑设计新的过渡段参考弹道来逐渐消除弹道偏差,尽量避免产生控制饱和问题。
设过渡参考弹道为连接实际启控点Pc1(x1,y1,z1)和方案弹道上参考点Pc2(x2,y2,z2)的曲线弹道,同时将过渡参考弹道曲线在纵向、侧向平面内进行分解。以纵向平面的过渡参考弹道曲线设计为例,采用函数y=aLx3+bLx2+cLx+dL对连接实际启控点和方案弹道上参考点的过渡参考弹道曲线进行拟合。
(10)
同时,由制导炮弹飞行运动学关系,选择的过渡参考弹道需满足实际启控点和方案弹道参考点的纵向飞行速度方向约束dy/dx=tanθsecψv,于是有:
(11)
联立可得纵向平面的参考弹道曲线系数为
(12)
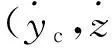
(13)
式(13)中的弹道倾角、弹道偏角的偏导数由过渡参考弹道或方案弹道提取。
3弹道跟踪仿真与分析
为了考核弹道跟踪控制方法对启控点误差、气动偏差和风场等的鲁棒性能,设置了2种弹道环境。情况1:考虑启控点位置和速度扰动的影响,启控点弹道参数偏差Δx=1 km,Δy=0.5 km,Δz=0.5 km,Δθ=-5°,Δψv=2°;根据风洞试验可获得先验气动参数最大误差,假设气动偏差ΔCx/Cx=5%,ΔCy/Cy=-10%。情况2:在情况1的条件下增加常值风干扰wy=-10 m/s,wz=10 m/s。
弹道跟踪控制器的切换增益根据气动误差、风场的界设定,以保持闭环控制系统的鲁棒性,并采用了边界层方法以减轻控制的抖振现象。
令边界层厚度φ=1.5时,实线为情况1下的实际弹道1,虚线为情况2下的实际弹道2。若进一步提高位置跟踪精度,设边界层厚度φ=0.5,点划线代表对应情况2下的实际弹道3。图3、图4反应了制导弹药受控后位置偏差的变化历程。制导弹药质心运动的动态过程主要取决于滑模面的特性,2种情况下的飞行轨迹基本重合,表明本文的控制器同时对初始扰动、风和气动参数偏差等具备鲁棒性,可完成对方案弹道的跟踪。由于边界层参数小,实际弹道3的位置跟踪精度高于实际弹道1和实际弹道2。观察到制导弹药在各种情况下均是按过渡参考弹道或预设方案弹道飞行,因而实际飞行弹道历程的性能可由弹道设计和弹道跟踪来保证。
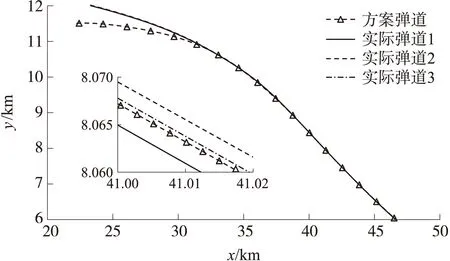
图3 采用滑模控制的射程-高度弹道曲线
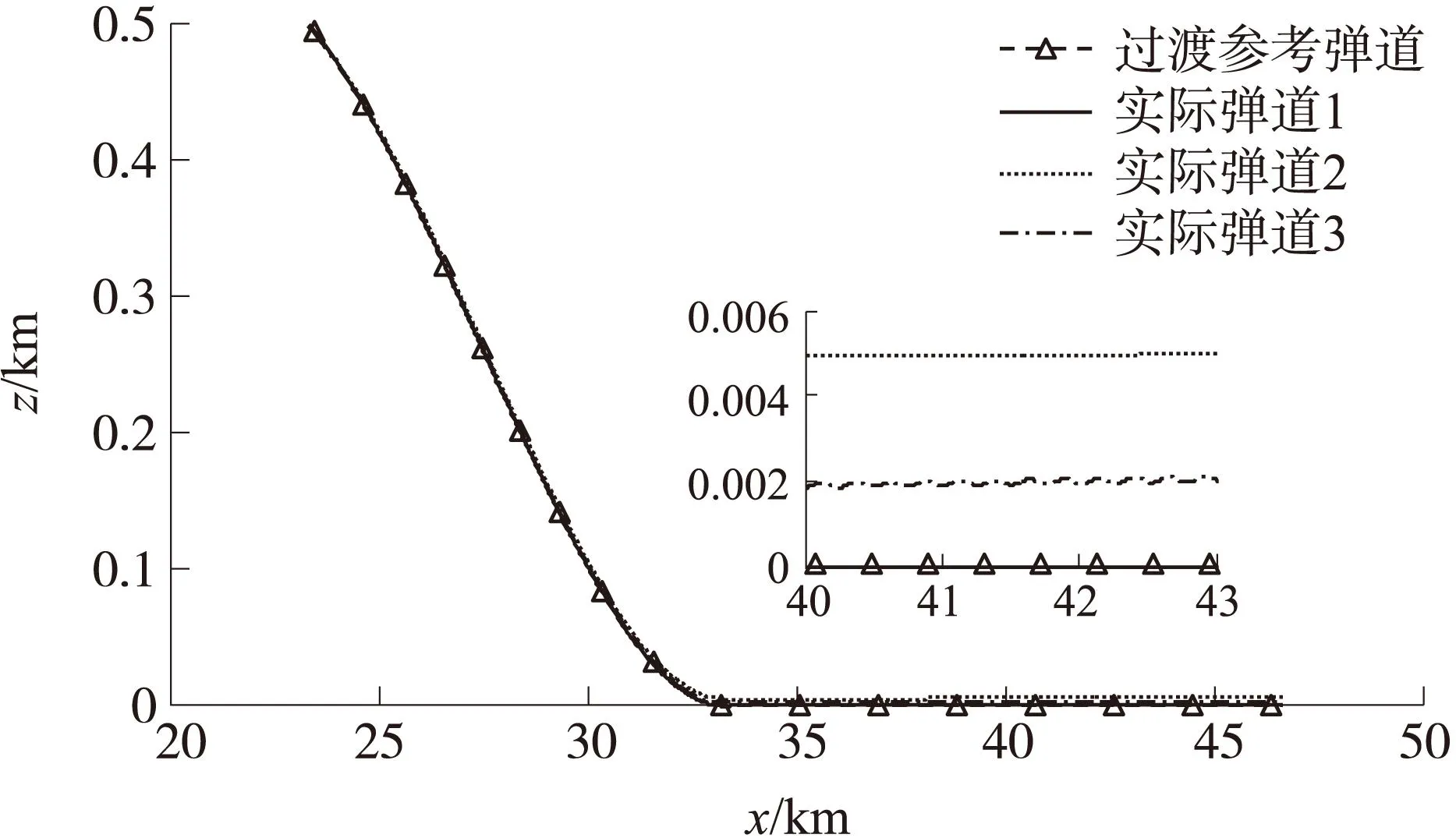
图4 采用滑模控制的射程-侧偏弹道曲线
图5显示方案弹道与实际弹道的速度变化曲线存在差异,且实际弹道2比实际弹道1的速度略有减小。产生速度差异的主要因素有:气动参数误差和气流姿态角之间的差异。由于设置的边界层参数较小,实际弹道3对应的飞行状态为了保持滑模状态,使得姿态角呈现为一定幅值的震荡现象,增加了诱导阻力,因而速度较实际弹道2衰减更快。

图5 采用滑模控制的速度随时间的变化曲线
图6、图7分别为弹道倾角和偏角曲线。闭环控制系统状态在滑模控制的作用下快速逼近滑动面,弹道倾角和偏角运动规律主要根据方案弹道和滑模模态进行变化。由于控制不连续和弹体惯性作用,理论控制精度更高的实际弹道3在期望值附近振荡。

图6 采用滑模控制的弹道倾角随射程的变化曲线
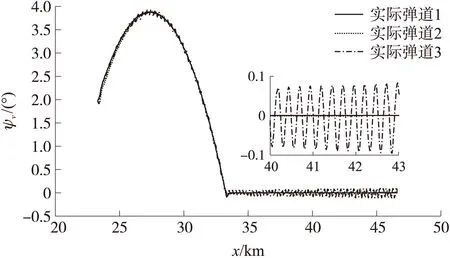
图7 采用滑模控制的弹道偏角随射程的变化曲线
图8、图9所示的攻角、侧滑角曲线反应了对实际弹道的气动控制策略,由于引入了合适的边界层,实际弹道1、实际弹道2中姿态角控制量均较为平滑。通过姿态调节产生相应的法向控制力使实际弹道的启控误差收敛,然后以合适的正攻角沿方案弹道飞行。
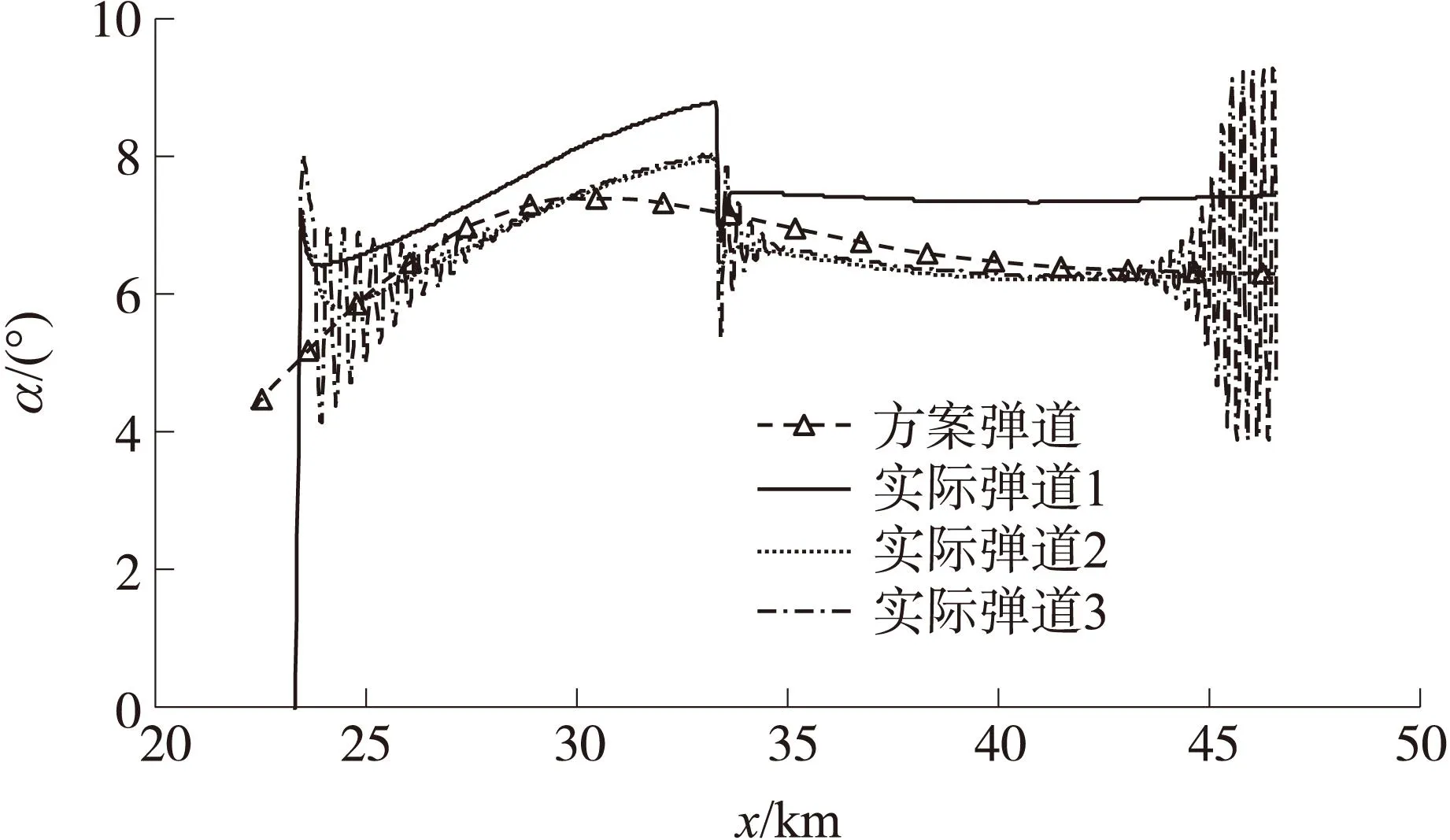
图8 采用滑模控制的攻角随射程的变化曲线
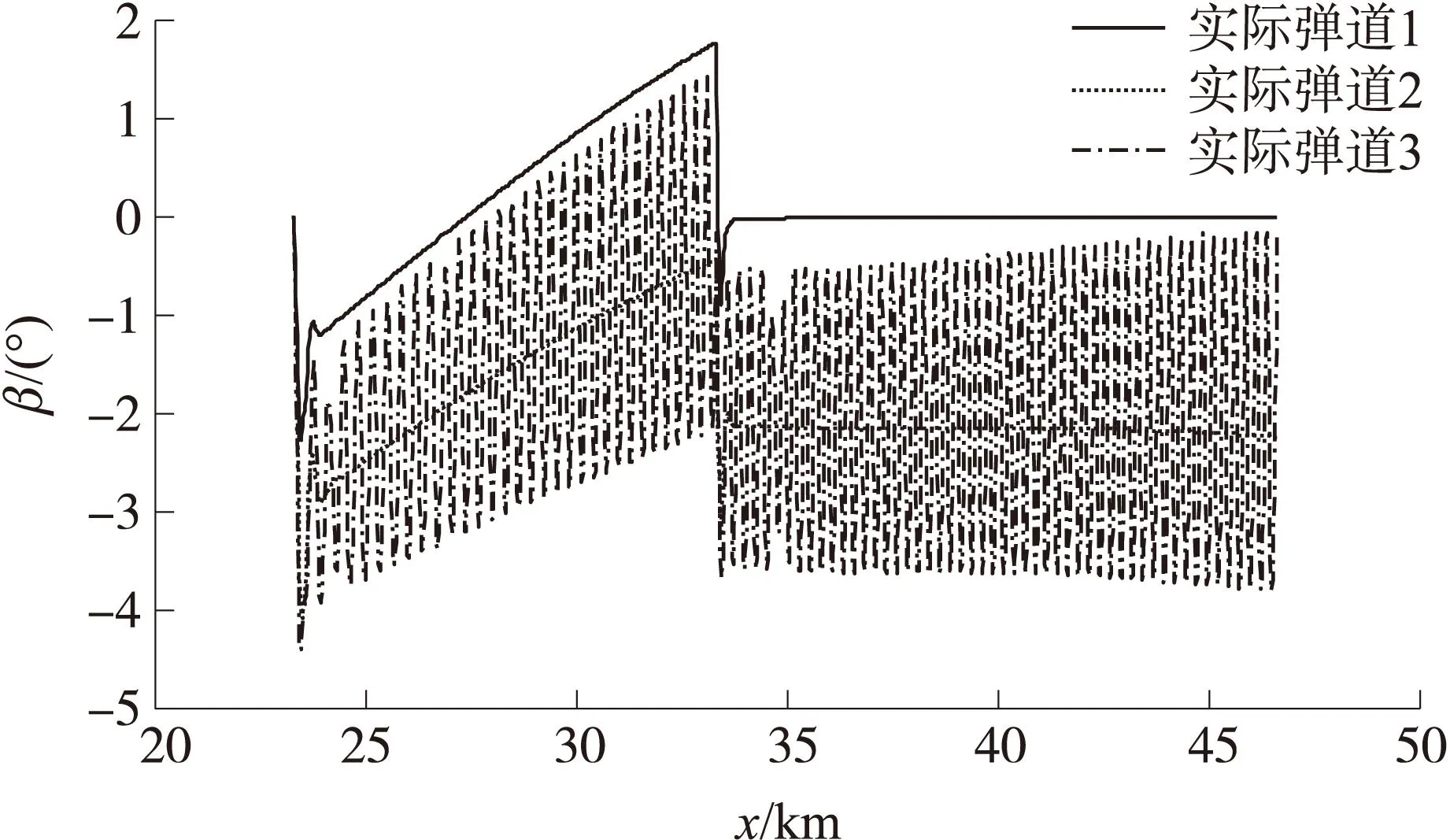
图9 采用滑模控制的侧滑角随射程的变化曲线
考虑侧向风的作用,制导弹药将以负的侧滑角飞行,使弹道保持在铅直面内。同时观察到:因为边界层厚度设置较小,在处理存在气动误差和风干扰的情况下,实际弹道3中的攻角和侧滑角在快速响应的动态控制阶段存在抖振。攻角与侧滑角的抖振不仅增加了姿态回路实现上的难度,同时增大了姿态角的幅值,容易诱发控制饱和。
抖振主要是由滑模控制中的鲁棒切换项产生的,可通过增大边界层厚度进一步平滑抖振,然而这同时也降低了对飞行弹道的跟踪精度。像其他类型的鲁棒控制方法一样,滑模控制也存在鲁棒性与控制精度之间的权衡问题。与气动参数的误差相类似,风的干扰也作为一个扰动因素影响着制导弹药的飞行运动,实际应用中应尽量保证控制模型的准确性,并保证飞行试验环境以获得满意的弹道跟踪控制效果。
4结束语
本文针对制导弹药方案弹道的实现问题,论述了基于滑模控制策略的弹道跟踪技术。基于动态逆和滑模控制理论设计了适用于制导弹药方案弹道跟踪的质心控制器,利用弹道滤波获得方案弹道指令的导数信息。通过李雅普诺夫理论和数值仿真验证了存在气动参数误差、外部扰动时闭环控制系统的鲁棒性能。
通过理论和数值分析得到以下结论:
①过渡参考弹道渐进消除初始误差的弹道是从几何运动关系导出,可进一步考虑飞行动力学设计性能优良的过渡参考弹道。
②采用滑模控制策略可以使实际弹道较严格地沿预设方案弹道飞行,并且可通过调整边界层来控制弹道跟踪的稳态误差。滑模控制的鲁棒性是以高频控制增益量为代价的,在应用滑模控制实施弹道跟踪任务时,设计的控制律需综合考虑控制精度与抖振现象。
参考文献
夏群力,郭涛,祁载康.空地导弹对应不同驾驶仪下的中制导高度控制回路设计.系统仿真学报,2008,20(24):6 763-6 766.
XIAQun-li,GUOTao,QIZai-kang.Designofaltitudecontrolloopsrelatingtodifferentautopilotsforair-to-groundmissilesmidcourseguidance.JournalofSystemSimulation,2008,20(24):6 763-6 766.(inChinese)
SANGHYUKP.PerformanceandLyapunovstabilityofanonlinearpath-followingguidancemethod.JournalofGuidance,Control,andDynamics,2007,30(6):1 718-1 727.
REINERJ,BALASGJ,GARRADWL.Robustdynamicinversionforcontrolofhighlymaneuverableaircraft.JournalofGuidance,Control,andDynamics.1995,18(1):18-24.
WANGXH,LIUJK,CAIYK.Trackingcontrolforavelocity-sensorlessVTOLaircraftwithdelayedoutputs.Automatica,2009,45(12):936-943.
LEEKW.Adaptiveslidingmode3-DtrajectorycontrolofF/A-18modelviaSDUdecomposition//AIAAGuidance,NavigationandControlConferenceandExhibit.HonoluluHawaii:AIAA,2008:1-22.
杨荣军.旋转制导炮弹的飞行弹道及控制系统设计方法研究.南京:南京理工大学,2012.
YANGRong-jun.Studyonflyingtrajectoryandcontrolsystemdesignforrollingguidedprojectile.Nanjing:NanjingUniversityofScience&Technology,2012.(inChinese)
BOUADIH.Aircrafttrajectorytrackingbynonlinearspatialinversion//AIAAGuidance,Navigation,andControlConference.MinneapolisMinnesota:AIAA,2012:1-17.
Application of Sliding Mode Control on Trajectory Following
for Guided Munitions
YANG Rong-jun1,YE Yao2,YAN De-heng1,WANG Yin1
(1.The 28th Research Institute of CETC,Nanjing 210007,China;
2.School of Public Administration,Nanjing Agricultural University,Nanjing 210095,China)
Abstract:In order to make guided munitions follow the planned trajectory effectively,a three-dimensional sliding-mode trajectory tracking-control-system was proposed.The tracking control scheme based on the trajectory correction strategy was discussed,and the tracking controller was designed by combining the dynamic inversion method and sliding mode control with reaching law.The influence of the controller parameters on the closed-loop stability,chattering and the tracking performance were also analyzed.A transition reference trajectory was designed to avoid control saturation problem caused by the start location deviation,and the smooth control-command information was given according to the geometry relationship.The simulation shows that the sliding mode control can make guidance munitions fly along the planned trajectory,and it is strong robust to external disturbance.The setting of controller parameters is a tradeoff between the control precision and the chattering problem.
Key words:guided munitions;trajectory following;trajectory control;sliding mode control;nonlinear control
中图分类号:TJ413.6
文献标识码:A
文章编号:1004-499X(2015)04-0024-06
作者简介:杨荣军(1986- ),男,工程师,博士,研究方向为武器控制与信息化。E-mail:rongjun802@163.com。
收稿日期:2015-07-18

