吸气式超声速导弹爬升段轨迹在线规划与跟踪设计
明 超,孙瑞胜,白宏阳
(南京理工大学 能源与动力工程学院,南京 210094)
吸气式超声速导弹爬升段轨迹在线规划与跟踪设计
明超,孙瑞胜,白宏阳
(南京理工大学 能源与动力工程学院,南京 210094)
摘要:为解决吸气式超声速导弹如何最优地爬升到巡航状态的问题,提出了一种吸气式超声速导弹的爬升轨迹在线规划与跟踪控制设计方法。将爬升段弹道分解为2个相切的圆弧,利用数学几何方法,推导了两相切圆的相关参数及代数方程,建立了爬升段的参考轨迹,并通过动虚拟目标追踪法设计了参考轨迹的跟踪制导律,从而实现了基于两圆相切理论的爬升段轨迹在线规划与跟踪控制,最后以典型工况为例,进行了数字仿真验证,并与hp自适应伪谱法的优化结果进行了对比分析。仿真结果表明,参考轨迹与优化结果差别不大,能够准确跟踪参考轨迹,同时算法简单,便于工程实现。研究成果可为吸气式超声速导弹爬升段轨迹设计提供参考。
关键词:吸气式超声速导弹;爬升段轨迹;相切圆;动虚拟目标;在线规划与跟踪
吸气式超声速导弹以比冲高、推阻比大的吸气式冲压发动机作为其动力装置,具有突防能力强、射程远、机动灵活等优势[1-4]。为充分发挥冲压发动机高空巡航的性能优势,爬升段弹道设计需要解决如何最优地从冲压发动机开机点爬升到巡航状态,而且爬升段需要加速和爬高,对全弹道的性能影响较大,因此,对吸气式超声速导弹的爬升段弹道进行合理地设计具有重要的理论研究意义和工程应用价值。
近年来,以吸气式发动机为动力的飞行器以其高性能的优势而备受关注[6-11]。尚腾、王华[6-7]等对以冲压发动机为动力导弹的爬升段弹道的参考轨迹进行优化设计,但并未考虑爬升段轨迹的跟踪控制。李海军等针对再入机动飞行器,提出一种基于优化方法和轨迹线性化控制相结合的最优制导与控制方案,但其参考轨迹的生成算法复杂,不便于在线实时计算。吕翔等通过建立吸气式组合动力飞行器的马赫数-动压参考曲线,利用二分法迭代攻角跟踪参考轨迹,但采用迭代方法获取参考轨迹的设计过程较为繁琐。Olds[10]等提出了迎角的优化模型,以实现等动压爬升,但优化模型的设计参数较多,且只能通过优化方法确定,不能在线实时提供爬升制导指令;闫晓东[11]等在此基础上,提出了一种基于高度-速度曲线的等动压爬升方法,但不满足最优性条件。综上,目前爬升段轨迹设计方法研究的不足之处主要集中在参考轨迹和制导指令在线实时计算不能保证,以及设计过程较为繁琐。
为此,本文以吸气式超声速导弹为研究对象,基于两圆相切理论和动虚拟目标导引方法,提出一种爬升段在线轨迹在线规划与跟踪控制方法,利用数学几何方法,推导了两相切圆的相关参数及代数方程,在线快速生成爬升段的参考轨迹,并通过动虚拟目标导引方法对参考轨迹进行实时跟踪制导,为吸气式超声速导弹爬升段轨迹工程设计提供参考。
1爬升段轨迹分析
1.1动力学模型
采用球体模型,忽略地球自转和地球曲率的影响,假设系统始终处于瞬时平衡状态,则吸气式超声速导弹运动的动力学模型可简化为[12]
(1)
式中:v,θ和L分别为导弹的飞行速度、弹道倾角和射程;r为地心距;H为高度,Re为地球半径;g为重力加速度;阻力Fx=qSrefCx,升力Fy=qSrefCy,由动压q和气动特性决定;Sref为参考面积;mc为发动机的燃料质量流量。
发动机推力Fp可由式(2)计算[13]:
Fp=Isp(H,Ma,α)mc
(2)
式中:Ma为飞行马赫数,Isp(H,Ma,α)为发动机比冲,以表格的形式给出。
1.2爬升段轨迹形式
从原理和经验分析可知,爬升段的弹道AB的中间会出现弹道倾角的拐点C,使得弹道倾角先从0°增加到拐点值,再逐渐减小到达巡航状态[14],如图1所示。
在图1中,起始点A(L0,H0)的状态:H0为起始高度,发射后助推段时间很短,不失一般性弹道倾角初值θ0=0°。终点B(LT,HT)的约束条件:HT为期望的巡航高度,弹道倾角θT因巡航平飞近似取为0°。
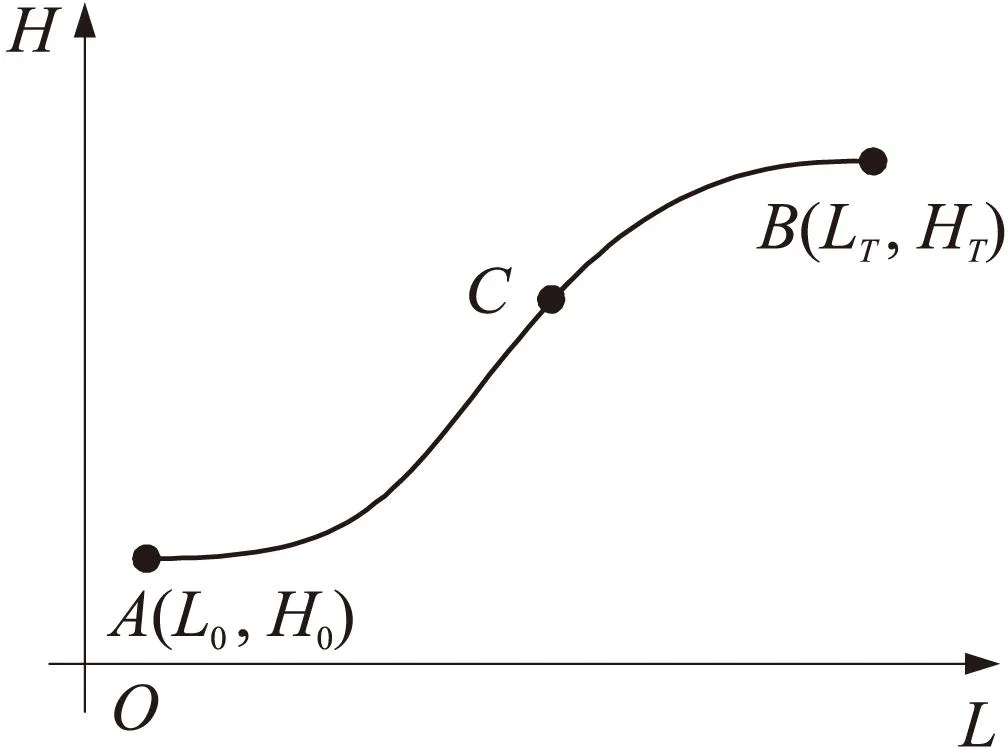
图1 爬升段轨迹形式
2轨迹在线规划设计
2.1问题描述

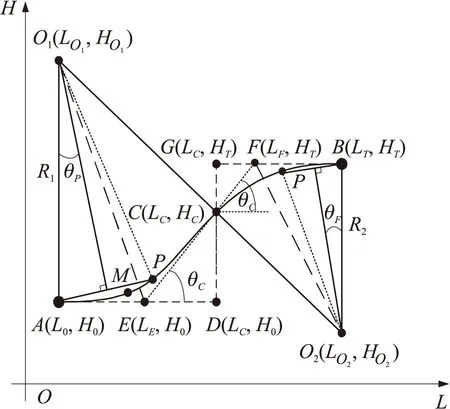
图2 爬升段轨迹辅助曲线图
2.2拐点信息
爬升段弹道AB的中间会出现弹道倾角的拐点C,当轨迹在线规划时,需确定拐点C的坐标C(LC,HC)及对应的弹道倾角θC。
由图2的几何关系,有:
(3)
(4)
联立式(3)、式(4),可求解出线段AE和线段BF的表达式为
(5)
根据G、C和D三点的几何关系,有:
GD=GC+CD=HT-H0
(6)
联立式(3)~式(6),得到:
(7)
将式(7)进行简化,并结合三角函数关系式,有:
(8)
求解方程组(8),即可求解出切点C处的弹道倾角θC,其表达式为
(9)
由式(9)可以看出,切点C处的弹道倾角θC为确定值,其大小只取决于导弹爬升段的起点和终点的位置信息。
不失一般性,简化取爬升段轨迹的中点[14]作为C点进行研究。
切点C点的横坐标LC为
(10)
切点C处的纵坐标HC为
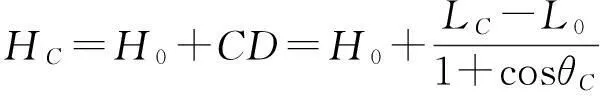
(11)
2.3爬升段参考轨迹

根据圆O1中的角度关系,可知:
(12)
在ΔAO1E中,利用直角三角形理论,可确定圆O1的半径R1为
(13)
圆心O1的坐标O1(LO1,HO1)为
LO1=L0,HO1=H0+R1
(14)
进而得到圆O1的代数方程为
(15)
同理,可推导出圆O2的半径R2和圆心坐标O2(LO2,HO2)表达式为
(16)
LO2=LT,HO2=HT-R2
(17)
圆O2的代数方程为
(18)
3轨迹跟踪设计
本文采用动虚拟目标导引方法实现对爬升段参考轨迹的跟踪制导。令虚拟目标点沿着设计的参考轨迹飞行,假定其速度与导弹一致,每一时刻的位置较导弹超前,导弹采用比例导引法跟踪动虚拟目标,从而通过动虚拟目标的引导作用实现对参考轨迹的跟踪。
3.1动虚拟目标点位置
吸气式超声速导弹爬升段起始点的信息A(L0,H0,S0),S0为飞行路程的初始值,导弹的当前点M(L,H,S),S为导弹的飞行路程,动虚拟目标点位置较导弹每一时刻位置超前,超前量记为ΔS,则虚拟目标点P(LP,HP,SP)的飞行路程SP为
SP=S+ΔS
(19)


SAP=SP-S0
(20)
根据弧长计算公式,可得到圆心角∠AO1P为
(21)
进而得到:
(22)
由直角三角形边角关系,有:
AP=2O1AsinθP=2R1sinθP
(23)
根据两点间距离计算公式,可得:
(24)
联立式(23)和式(24),有:
(LP-L0)2+(HP-H0)2=(2R1sinθP)2
(25)
虚拟目标点P(LP,HP)在圆O1上,从而满足方程:
(26)

(27)
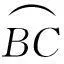
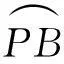
SPB=SAC+SCB+S0-SP
(28)

对应的圆心角∠BO2P为
(29)
进而有:
(30)
由几何关系,可得:
BP=2O2BsinθP=2R2sinθP
(31)
根据两点间距离计算公式有:
(32)
联立式(31)和式(32),有:
(LP-LT)2+(HP-HT)2=(2R2sinθP)2
(33)
虚拟目标点P(LP,HP)在圆O2上,因此满足:
(34)

(35)
3.2制导指令
吸气式超声速导弹采用比例导引法跟踪动虚拟目标,从而通过动虚拟目标的引导作用实现对参考轨迹的跟踪,比例导引律的基本形式[15]为
(36)
视线角速度为
式中:Kq为比例导引系数,RL=L-LP, RH=H-HP,L和H分别为导弹的位置分量,vL和vH分别为导弹的速度分量。
导弹的制导过载指令为
(37)
根据导弹的动力学方程,过载可表示为[15]
(38)
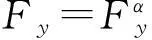
(39)
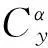
联立以上各式,可得到爬升段的飞行攻角制导指令为
(40)
4优化仿真与结果分析
以某吸气式超声速导弹为例,对爬升段轨迹在线规划与跟踪算法进行仿真验证。为了验证文中方法的合理性,分别采用以下2种方案对爬升段轨迹进行对比仿真分析。
方案1:采用hp自适应伪谱法[16-18]对爬升段轨迹进行优化设计,优化设计变量为飞行攻角α和燃料质量流量mc,选取燃料最省[19],即油耗mu最小作为优化的性能指标。
方案2:采用前文提出的爬升段在线规划与跟踪算法进行设计,冲压发动机的燃料质量流量采用方案1的优化结果进行调节。
4.1参数设置
吸气式超声速导弹爬升段优化设计的状态变量的初始条件设定为:Ma0=2.9,θ0=0°,L0=0,H0=15 km,m0=500 kg;飞行轨迹终端的设计约束条件为:Maf=3.0,θf=0°,Lf=45 km,Hf=20 km,其中,轨迹优化设计变量的约束条件设定为:0.2 kg/s≤mc≤1.2 kg/s,-2°≤α≤12°,虚拟目标导引法中的比例导引系数为Kq=2,超前量为ΔS=4 km。
4.2仿真结果分析
采用4.1节中的仿真参数,分别对2种方案下的吸气式超声速导弹爬升轨迹进行仿真,表1给出了2种方案下的爬升段弹道性能数据,对比仿真结果如图3~图8所示。

表1 弹道性能对比数据
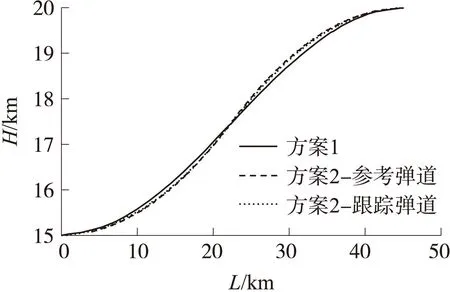
图3 弹道曲线
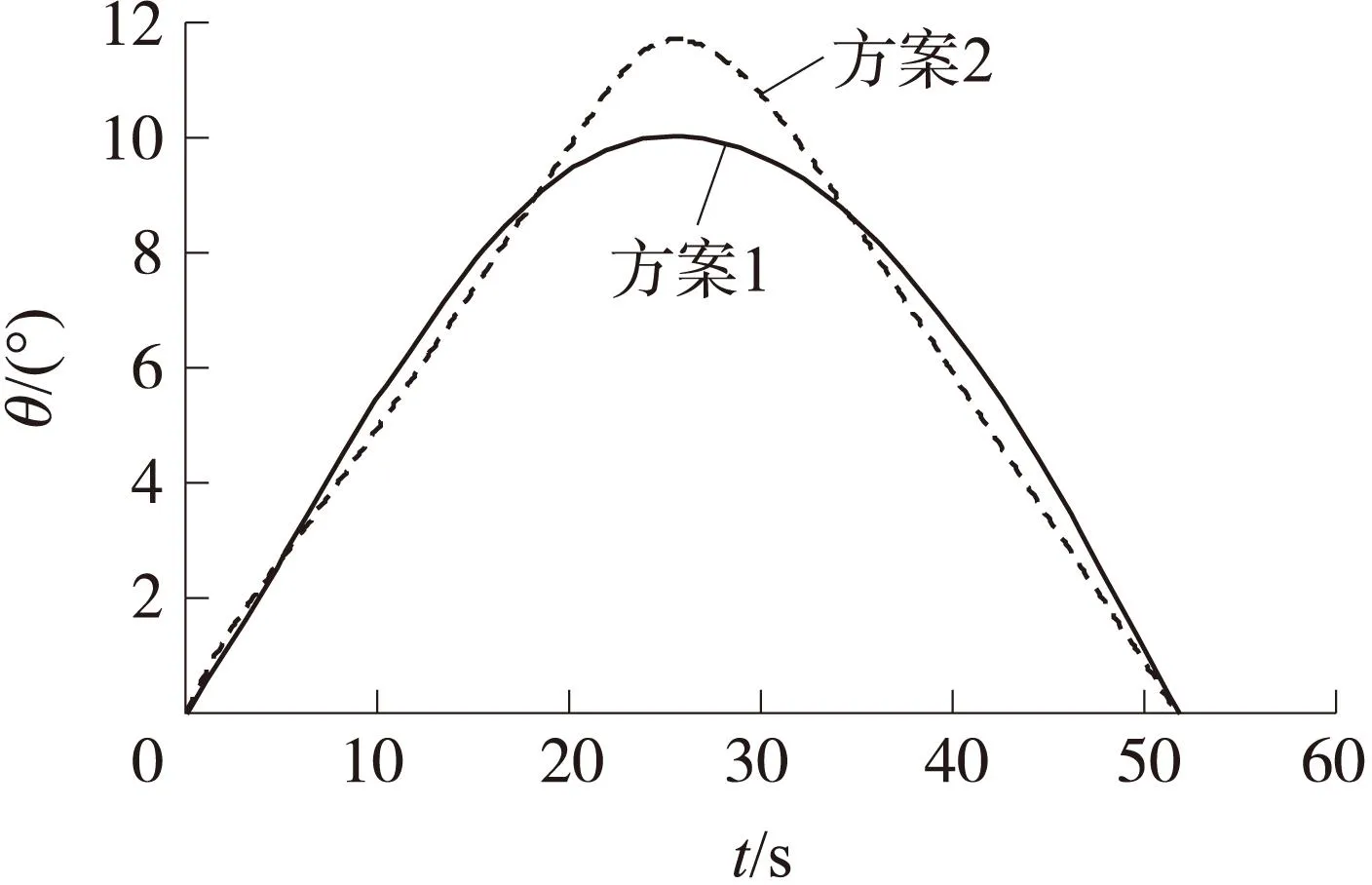
图4 弹道倾角变化曲线

图5 马赫数变化曲线
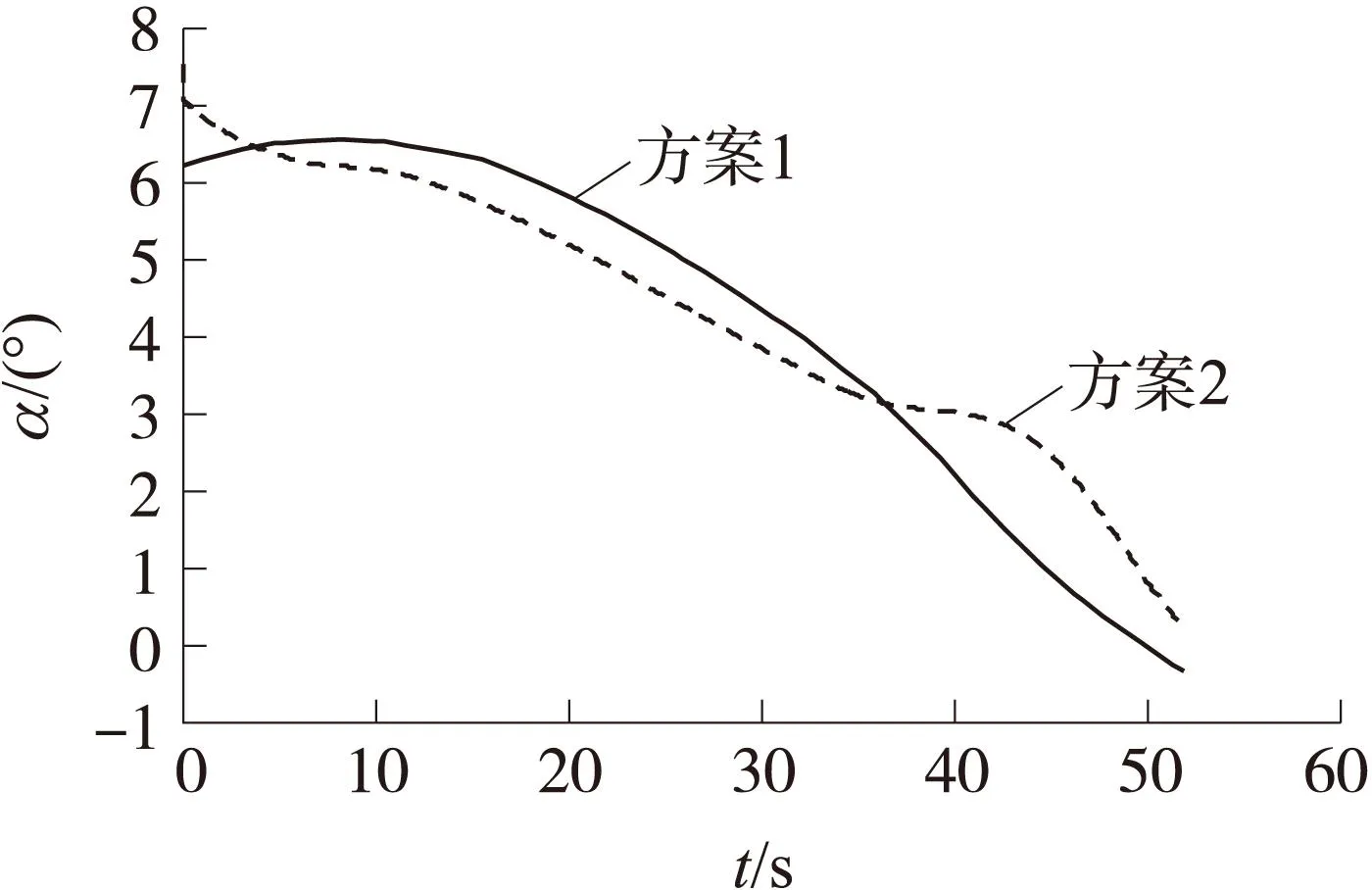
图6 攻角变化曲线
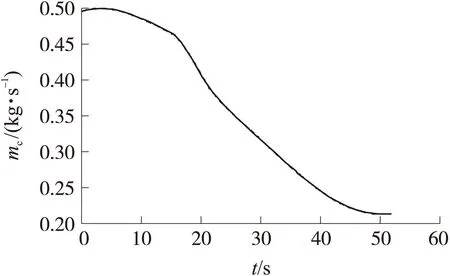
图7 燃料质量流量变化曲线

图8 推力变化曲线
仿真结果表明:2种方案下的爬升段轨迹设计均满足设计要求。从表1可以看出,2种方案下的油耗约为18.5 kg,相差不大。图3为吸气式超声速导弹爬升段轨迹的对比曲线,实线表示采用优化方法设计的爬升轨迹,虚线表示在线规划的参考轨迹,点线表示实际的跟踪曲线。由各仿真曲线可以看出,在线规划的爬升段轨迹与优化设计的轨迹差别不大,表明在线规划算法的正确性与最优性。在第3节制导指令求解过程中对升力系数进行了多项式拟合,存在模型的不确定性。从仿真结果可以看出,在存在模型误差的情况下,动虚拟目标追踪法仍能具有良好的制导效果,可实现对参考轨迹的准确跟踪,表明了动虚拟目标制导算法的正确性。
5结束语
①针对吸气式超声速导弹爬升段轨迹设计问题,提出了一种两圆相切理论的爬升段轨迹在线规划方法,该算法设计过程简单,只需输入起点和终点坐标,便于工程实现。
②提出了爬升段参考轨迹跟踪的动虚拟目标追踪法,在存在模型误差的情况下,该算法具有良好的抑制作用,可实现对参考轨迹的准确跟踪。
③通过与hp自适应伪谱法的爬升段轨迹对比仿真,以最小油耗为性能指标,2种方案下的最小油耗约为18.5 kg,仿真结果表明该在线规划与跟踪算法的最优性和合理性。
参考文献
MA J,LIANG J L.Development trends and directions of liquid ramjet/scramjet technology.Journal of Rocket Propulsion,2011,37(4):12-17.
方洋旺,柴栋,毛东辉,等.吸气式高超声速飞行器制导与控制研究现状及发展趋势.航空学报,2014,35(7):1 776-1 786.
FANG Yang-wang,CHAI Dong,MAO Dong-hui,et al.Status and development trend of the guidance and control for air-breathing hypersonic vehicle.Acta Aeronoutica et Astronautica Sinica,2014,35(7):1 776-1 786.(in Chinese)
HENRY J R,MCLELLAN C H.Air-breathing launch vehicle for earth-oribit shuttle new technology and development approach.Journal of Aircraft,1971,8(5):381-387.
黄琳,段志生,杨剑影.近空间高超声速飞行器对控制科学的挑战.控制理论与应用.2011,28(10):1 496-1 505.
HUANG Lin,DUAN Zhi-sheng,YANG Jian-ying.Changll-enges of control science in near space hypersonic aircrafts.Control Theory and Application,2011,28(10):1 496-1 505.(in Chinese)
王华,杨存富,刘恒军.以冲压发动机为动力的导弹爬升弹道优化.弹箭与制导学报,2008,28(3):185-187.
WANG Hua,YANG Cun-fu,LIU Heng-jun.Optimization research on climb trajectory for a ramjet powered missile.Journal of Projectiles,Rockets,Missiles and Guidance,2008,28(3):185-187.(in Chinese)
尚腾,谷良贤,赵吉松.冲压发动机导弹爬升轨迹与推力调节规律优化.飞行力学,2012,30(3):280-283.
SHANG Teng,GU Liang-xian,ZHAO Ji-song.Integrated optimum design for ramjet missile climb trajectory and thrust regulation.Flight Dynamic,2012,30(3):280-283.(in Chinese).
王华,杨存富,刘恒军.以冲压发动机为动力的导弹爬升弹道研究.现代防御技术,2008,33(2):27-30.
WANG Hua,YANG Cun-fu,LIU Heng-jun.Research on climb trajectory of ramjet engine powered missile.Modern Defence Technology,2008,33(2):27-30.(in Chinese)
李海军,黄显林,葛东明.再入机动飞行器最优轨迹设计与跟踪.系统工程与电子技术,2010,32(9):1 951-1 956.
LI Hai-jun,HUANG Xian-lin,GE Dong-ming.Optimal trajectory design and tracking for maneuver reentry vehicles.Systems Engineering and Electronics,2010,32(9):1 951-1 956.(in Chinese)
吕翔,何国强,刘佩进.RBCC飞行器爬升段轨迹设计方法.航空学报,2010,31(7):1 331-1 337.
LV Xiang,HE Guo-qiang,LIU Pei-jin.Ascent trajectory design method for RBCC-powered vehicle.Acta Aeronautica et Astronautica Sinica,2010,31(7):1 331-1 337.(in Chinese)
[10] OLDS J R,BUDIANTO I A.Constant dynamic pressure trajectory simulation with POST,AIAA 98-302.1998.
[11] 闫晓东,贾晓娟,吕石.RBCC动力飞行器等动压爬升方法.固体火箭技术,2013,36(6):711-714.
YAN Xiao-dong,JIA Xiao-juan,LV Shi.A ascent trajectory design method with constant dynamic pressure for RBCC powered vehicle.Journal of Solid Rocket Technology,2013,36(6):711-714.(in Chinese)
[12] 赵汉元.飞行器再入动力学与制导.长沙:国防科技大学出版社,1997.
ZHAO Han-yuan.Spacecraft reentry dynamics and guidance.Changsha:National University of Defense Technology Press,1997.(in Chinese)
[13] 孟斌.高超声速巡航导弹弹道设计与优化方法研究.哈尔滨:哈尔滨工业大学,2007.
MENG Bin.Method research on trajectroy design and optimization of hypersonic cruise missile.Harbin:Harbin Institute of Technology,2007.(in Chinese)
[14] 邢立伟,吕俊巧.一种飞行器的爬升弹道闭环优化技术研究.战术导弹技术.2013,21(5):20-24.
XING Li-wei,LV Jun-qiao.Close-loop optimization research on the climing trajectory of a kind of aerocraft.Tactical Missile Technology,2013,21(5):20-24.(in Chinese)
[15] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学.北京:北京理工大学出版社,2000.
QIAN Xing-fang,LIN Rui-xiong,ZHAO Ya-nan.Flight dynamics of missiles.Beijing:Beijing Institute of Technology Press,2000.(in Chinese)
[16] DARBY C L,HAGER W W,RAO A V.An hp-adaptive pseudospectral method for solving optimal control problem.Optimal Control Application and methods,2011,32(4):476-502.
[17] GILL P E,MURRAY W,SAUNDERS M A.SNOPT:an SQP algorithm for large scale constrained optimization.SIAM Journal on Optimization,2002,12(4):979-1006.
[18] DARBY C L,HAGER W W,RAO A V.Direct trajectory optimization using a variable low-order adaptive pseudo-spectral method.Journal of Spacecraft and Rockets,2011,48(3):433-445.
[19] 施雨阳,万自明,徐敏.冲压发动机导弹爬升轨迹/发动机一体化优化设计.计算机仿真,2013,30(10):138-142.
SHI Yu-yang,WANG Zi-ming,XU Min.Integrate optimization design of climb trajectory and motor for ramjet powered missile.Computer Simulation,2013,30(10):138-142.(in Chinese)

Design of Online Planning and Tacking Ascent Trajectory
for Air-breathing Supersonic Missile
MING Chao,SUN Rui-sheng,BAI Hong-yang
(School of Energy and Power Engineering,NUST,Nanjing 210094,China)
Abstract:To make the air-breathing supersonic missile(ASM)optimally climb to cruising state,an online planning and tracking method for ASM was proposed.The cruising phase was divided into two tangent circular-arcs.The relative parameters and algebraic equations of the two tangent circular arcs were derived by the geometric method.The reference trajectory was built,and a type of trajectory tracking guidance law was put forward by pursuing a virtual moving target.The online planning and tracking control of the ascent trajectory were implemented based on the theory of tangent circles.Taking some typical cases for instance,the verification was carried out by numerical simulation.By comparing with hp-adaptive pseudo-spectral method,the simulation results show that there is a bit difference between reference trajectory and optimal trajectory,and the reference trajectory can be tracked accurately.The proposed method can be applied to the engineering practice of the ascent trajectory design of ASM,and the research offers reference for the ascent trajectory design of ASM.
Key words:air-breathing supersonic missile;ascent trajectory;tangent circles;virtual moving target;online planning and tracking
中图分类号:TJ765;V412
文献标识码:A
文章编号:1004-499X(2015)04-0012-07
通讯作者:孙瑞胜(1978- ),男,副教授,博士,研究方向为飞行器总体设计。E-mail:srscom@163.com。
作者简介:明超(1989- ),男,博士研究生,研究方向为飞行器轨迹优化与制导控制。E-mail:nust802mc@126.com。
基金项目:国家自然科学基金项目(11176012);江苏省普通高校研究生科研创新计划工程(KYLX15-0394)
收稿日期:2015-07-30

