推力矢量拦截弹制导控制一体化设计
惠耀洛,南 英,邹 杰
(1.南京航空航天大学 航天学院,南京 210016;2.国家光电重点实验室,河南 洛阳 471009)
推力矢量拦截弹制导控制一体化设计
惠耀洛1,南英1,邹杰2
(1.南京航空航天大学 航天学院,南京 210016;2.国家光电重点实验室,河南 洛阳 471009)
摘要:针对采用推力矢量控制的拦截弹,首先给出了推力矢量和气动力的归一化设计方法,通过引入等效舵偏角的概念,将多控制输入问题转化为单控制输入问题,并进行求解,设计了推力矢量偏心和气动舵偏转的控制分配策略,给出了气动舵偏转角及推力矢量偏心角的数学表达式,解决了多控制量之间相互争斗的问题。在此基础上,通过模型标准化,采用Backstepping方法(反步法),借助Lyapunov再设计工具,对导弹制导与控制系统进行一体化设计,得到了俯仰平面内的制导控制律。仿真结果表明,和常规制导与控制方法分别设计相比,采用该制导控制一体化设计方法能够使拦截弹有效拦截机动目标,并且导弹的姿态和执行机构偏角的变化也更加平稳。
关键词:拦截弹;推力矢量;控制分配;制导控制一体化;反步法
推力矢量控制技术[1-4]可以使导弹在低速、高空的飞行状态下仍然能够产生较大的横向过载,显著改善导弹的机动性和可控性,第四代空空导弹以及大部分弹道导弹的助推飞行段都采用了推力矢量控制技术,但是推力矢量技术的引入又带了诸多问题:推力矢量装置的安装方式如何选择、推力矢量直接力和气动力的分配策略、推力偏心和发动机尾喷气流对弹体控制的影响等。因此,对于采用推力矢量控制技术的拦截弹,有必要研究制导控制一体化技术,以充分发挥推力矢量对拦截弹轨迹的控制作用,同时制导控制律应具有一定的抗干扰能力,能够有效抑制系统建模误差和外扰,从而使拦截弹准确命中目标。
自从Williams提出制导控制一体化概念后,该技术成为国内外制导控制领域研究的热点之一[6-17]。制导控制一体化将传统飞行器控制方法中的外环轨迹控制与内环姿态控制统一起来,由导弹和目标相对运动信息直接产生执行机构控制指令,不仅能够降低研发成本、提高系统可靠性,而且可以最大限度地发挥制导控制系统的性能。文献[12]通过把制导控制系统作为一个最优控制问题,采用状态依赖Riccati微分方程方法求取数值解,解决了三通道耦合的飞行器制导控制问题。文献[13]采用滑模变结构控制方法,设计了自适应非线性一体化导引与控制律。文献[14]针对地面固定目标采用滑模变结构控制方法研究了带末端角度约束的巡航导弹的制导控制一体化问题。文献[15]采用反馈线性化结合LQR方法设计了三通道耦合的制导控制一体化控制器。Backstepping设计方法是针对不确定系统的一种系统化的控制器综合方法,通过从系统的最低阶微分方程开始,通过选取Lyapunov函数并引入中间虚拟控制量,逐步设计出最终的控制律。文献[16]采用Backstepping控制方法设计了轨控式复合制导导弹的制导控制律,并且采用非线性干扰观测器对模型中的不确定性进行估计和补偿。文献[17]采用Backstepping控制方法设计了拦截机动目标的导弹制导控制律,并证明其在考虑目标机动和不确定性存在的条件下,视线角速率是输入到状态镇定的。本文首先对推力矢量拦截弹的执行机构控制量进行归一化设计,解决多输入控制变量的协作和分配问题,然后采用Backstepping方法,对推力矢量拦截弹进行制导控制一体化设计,数值飞行仿真表明,该方法可以最大程度地发挥推力矢量对拦截弹轨迹的控制作用,能够在保持拦截弹姿态稳定的前提下精确命中机动目标。
1推力矢量/气动力控制量归一化设计
定义推力矢量偏转角,如图1所示。
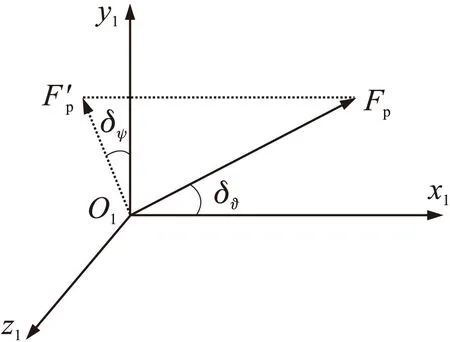
图1 推力矢量偏转角示意图
拦截弹主发动机喷管相对于弹体坐标系的摆角可分解为推力俯仰角δϑ和推力偏航角δψ,δϑ为推力矢量与弹体坐标系x1轴之间的夹角,δψ为推力矢量在弹体坐标系O1y1z1平面上的投影与y1轴的夹角。设推力大小为Fp,则推力在弹体坐标系各轴上的分量分别为
(1)
假设主发动机喷管口距拦截弹质心的距离为l,忽略推力矢量对拦截弹滚转通道的影响,可得推力矢量产生的力矩表达式为
(2)
式中:Mp,x、Mp,y和Mp,z分别为推力偏心产生的滚转力矩、偏航力矩和俯仰力矩。对整个弹体进行飞行力学仿真与分析可知,气动舵和发动机推力偏心主要对拦截弹姿态产生控制作用。以俯仰回路姿态控制系统为例,气动控制力矩的产生主要为气动俯仰舵产生的俯仰力矩(Mz1)和发动机推力偏心产生的俯仰力矩(Mz2)。
(3)
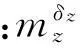
假设由气动俯仰舵和推力偏心各产生Mz1和Mz2的俯仰力矩,如果这些力矩由等效俯仰舵产生,则等效俯仰舵偏转量为
(4)
显然,
(5)
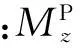
为兼顾减小拦截弹能耗和增强拦截弹的机动性,在舵面分配上,优先使用气动舵,当气动舵达到满偏时,保持气动舵面至此位置,同时开启推力矢量舵。由此得到俯仰舵偏转角和推力矢量偏转角的计算表达式:
(6)

(7)
式中:
2制导与控制一体化数学模型


(8)
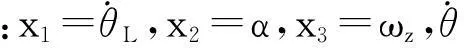
ξ=(ξ1ξ2ξ3)T+Δ,C=(100)
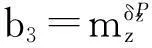
ξ1=atcos(θvt+θL)/r
ξ2=(mgcosθvm-Fpδϑ)/(mv)
ξ3=(mgcosθvm-Fpδϑ)cos(θvm-θL)/(mr)
将系统模型标准化,令:
得到:
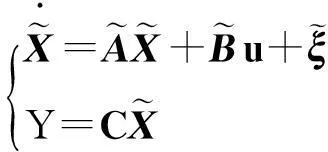
(9)
式中:
3基于Backstepping和Lyapunov再设计的制导控制一体化设计
将系统模型(9)标准化为
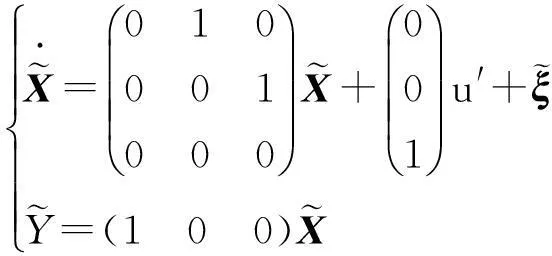
(10)
考虑存在系统未建模特性和不确定性干扰条件下的制导控制律设计。
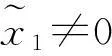

(11)
取状态反馈:
当Y>Y*时,dX1/dt>0,dX2/dt<0,则x2=1是演化稳定策略,政府激励无效的概率为1,此时购房者购买普通房,或者政府不奖励被动房的购房者,导致原来选择被动房的购房者转变为购买普通房,博弈收敛于帕累托劣均衡。
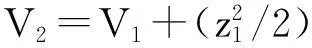
[(1+p)f1+f2]|z1|-z1υ1
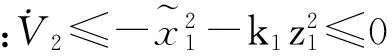

(12)
取:
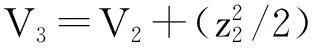
[k1(1+p)f1+(1+p+k1)f2+f3]|z2|-z2υ2
取:
υ2=[k1(1+p)f1+(1+p+k1)f2+f3]sgn(z2)
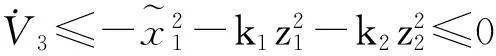

4数值仿真与分析
以目标在铅垂面内作正弦型机动飞行为例,设置拦截弹初始位置坐标(0,10km,0),初速500m/s,初始弹道倾角-30°,初始攻角-5°,发动机推力为20kN,比冲为233.37N·s/kg,持续时间23.3s,设定气动舵面偏转角范围为-25°~25°,推力矢量偏转角范围为-5°~5°。目标初始位置坐标(120km,25km,0),初速500m/s。制导律参数设置:k1=0.25,k2=0.15,p=0.5,f1=0.55,f2=0.48,f3=0.2。对推力矢量拦截弹1和拦截弹2分别采用PN制导+PID控制方法和本文的制导控制一体化方法,进行弹目飞行对抗仿真,仿真结果如图2~图9所示。
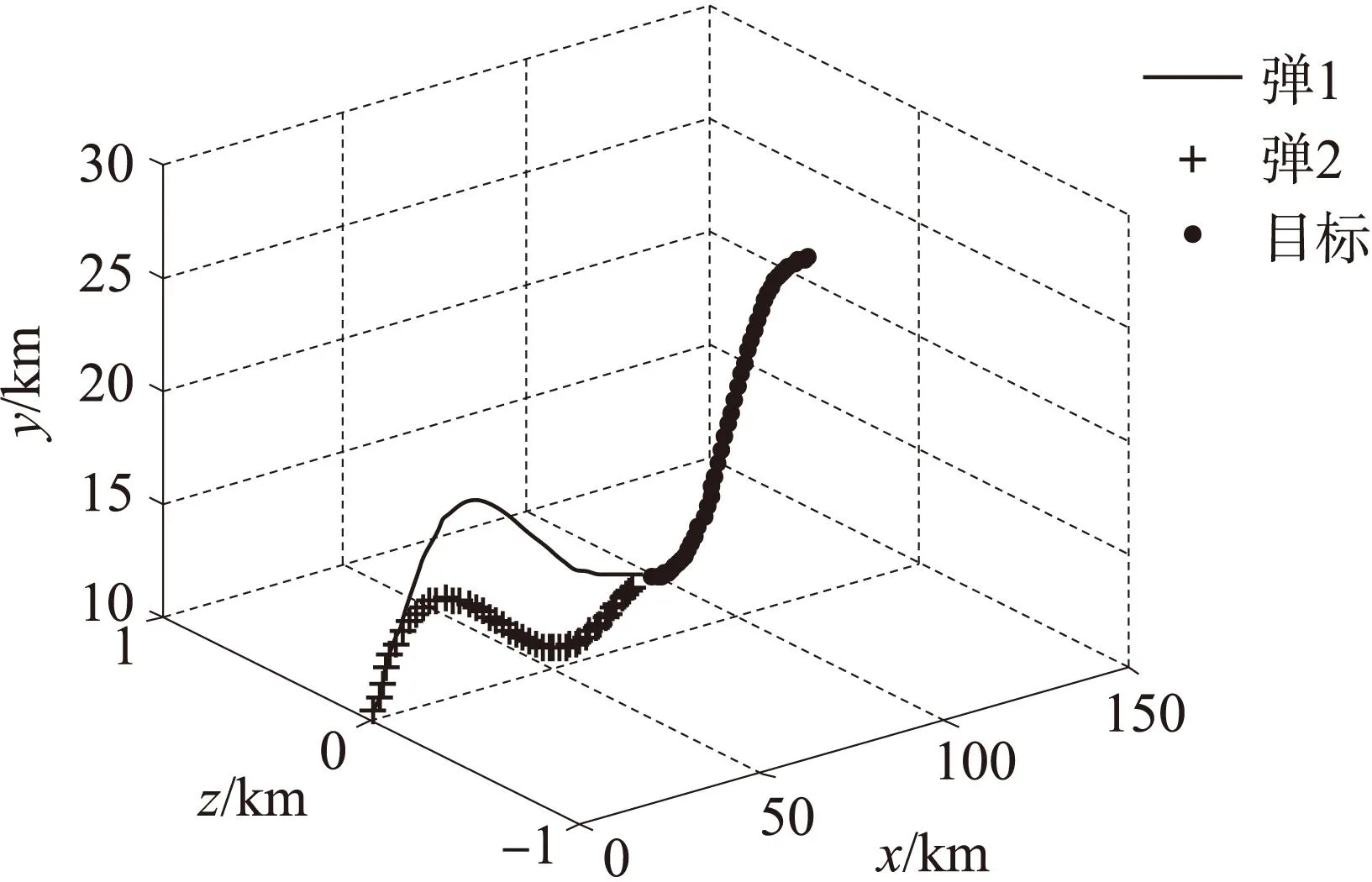
图2 拦截弹和目标的飞行轨迹
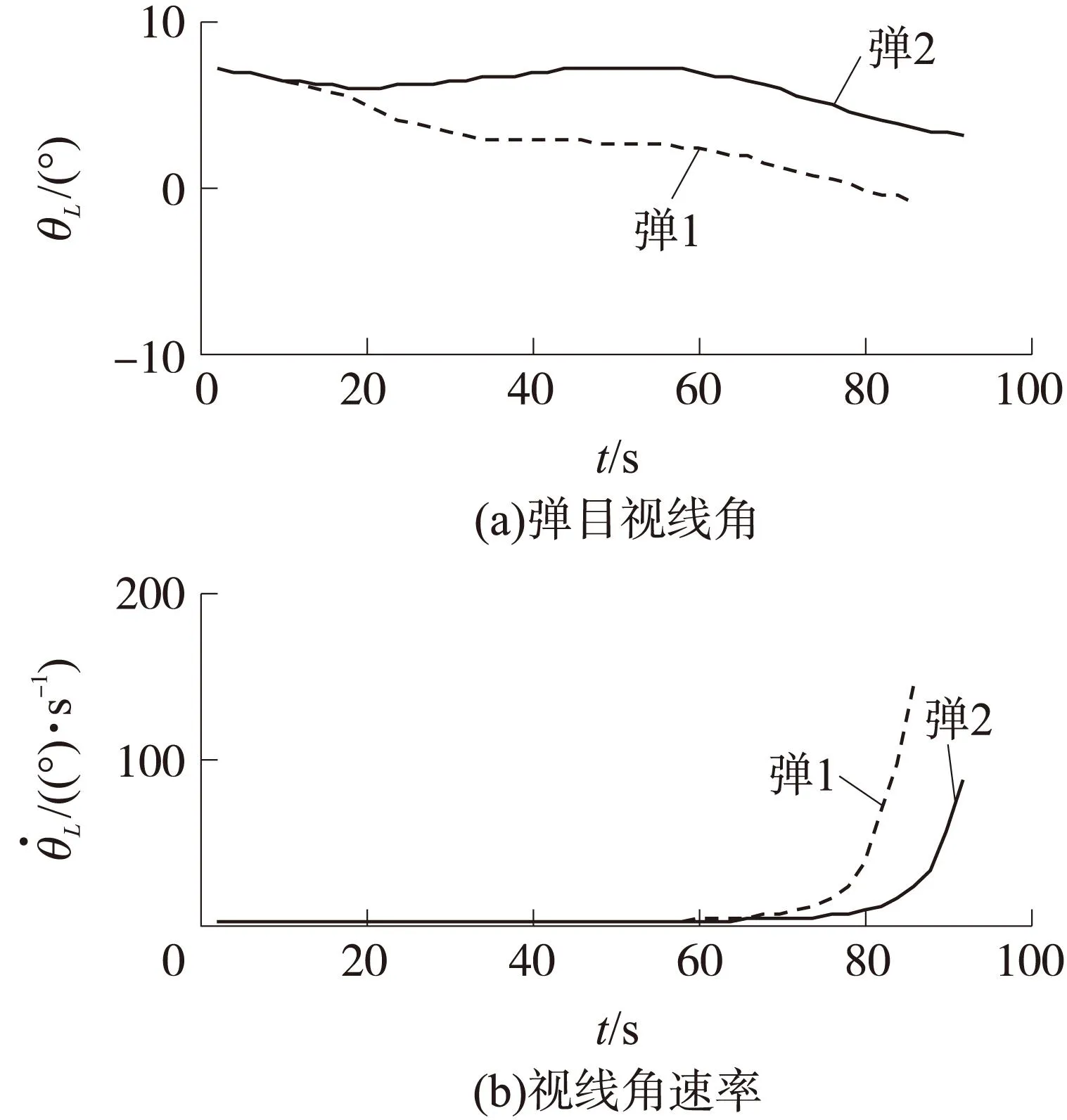
图3 弹目视线角和视线角速率随时间的变化
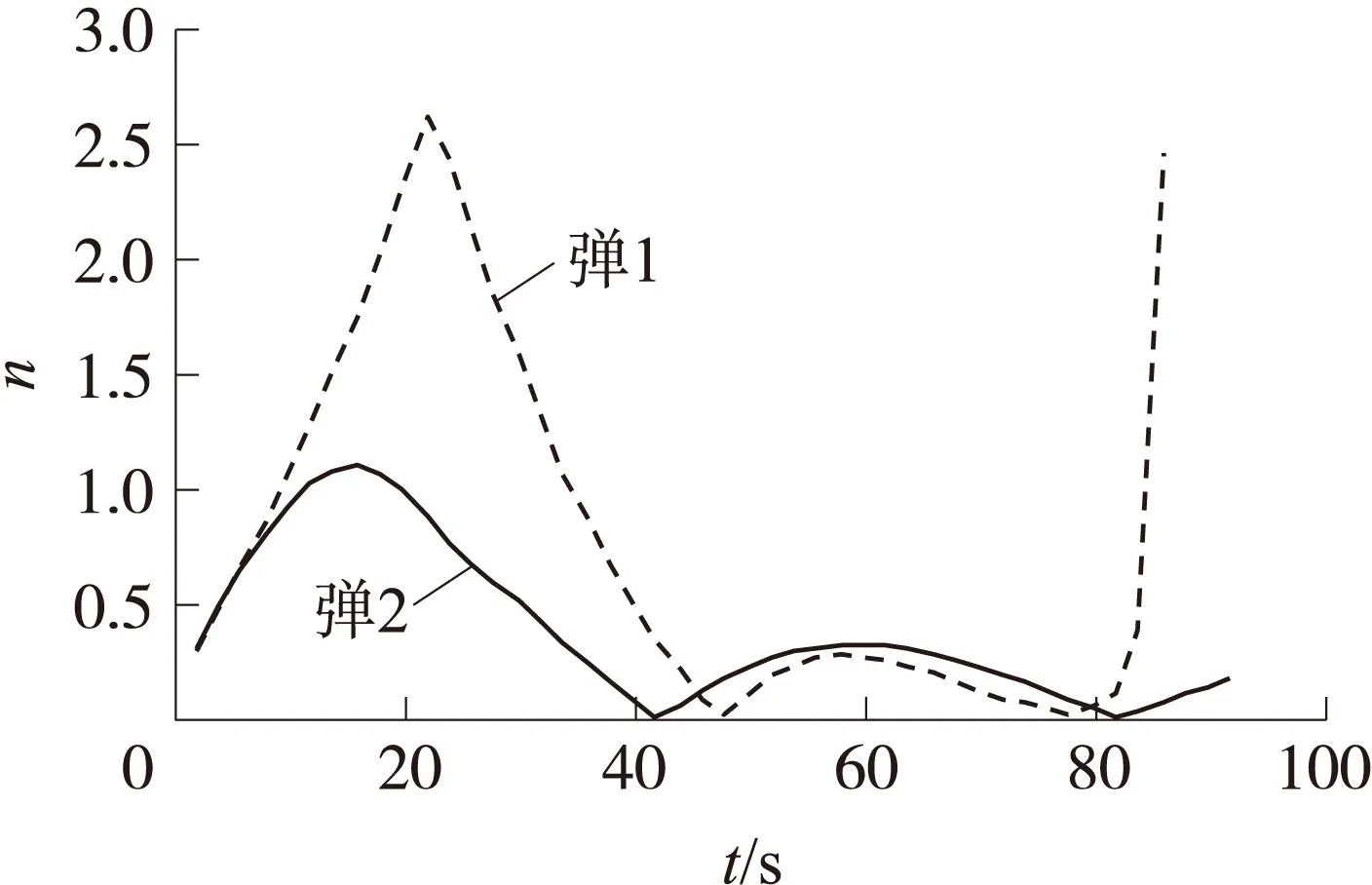
图4 拦截弹法向过载随时间的变化
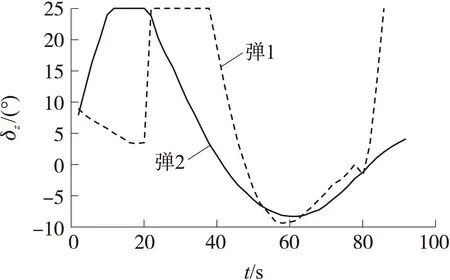
图5 舵偏角随时间的变化

图6 推力矢量角随时间的变化
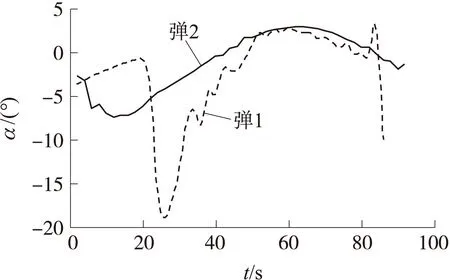
图7 拦截弹攻角随时间的变化

图8 拦截弹姿态俯仰角随时间的变化
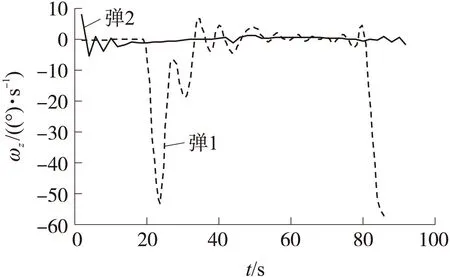
图9 拦截弹转动角速度随时间的变化
由图2知,拦截弹2比拦截弹1更能快速适应和跟踪目标飞行轨迹的变化,在目标作机动时,拦截弹2能够迅速转弯机动,这样可在导弹拦截末段有效减小脱靶量。
由图3知,拦截弹2的弹目视线角变化更加平缓,有利于自寻的制导阶段捕获和定位目标,在拦截末段拦截弹2的弹目视线角速率更小一些,也能使控制量的变化更加平稳,不易造成控制发散。由图4知,拦截弹1的平均需用法向过载和最大需用法向过载均大于拦截弹2,因此采用Backstepping制导控制一体化方法的导弹弹道更加平稳。
由图5和图6知,拦截弹 1和拦截弹 2在达到最大气动舵偏角25°后,舵偏角保持不变,开始启动推力矢量控制。拦截弹 2比拦截弹 1先开启推力矢量控制,且推力矢量偏角较小,仍然是因为采用Backstepping制导控制一体化方法的导弹的控制量能够快速适应目标变化,且变化较平稳。
由图7和图8知,拦截弹1的攻角和姿态俯仰角波动幅度大,容易使导弹失稳,而拦截弹 2的导弹姿态控制比较理想,攻角和姿态角都渐渐趋于稳定。由图9知,拦截弹 1的转动角速度较大,这也是造成导弹姿态波动的原因,从执行机构控制量变化和导弹弹道及最终脱靶量角度考虑,采用Backstepping制导控制一体化方法更具优势。
5结束语
本文研究了推力矢量拦截弹的制导控制一体化设计。对于存在推力矢量偏心的多控制输入系统,通过引入等效舵偏角的概念,将推力矢量偏转角和气动舵偏转角进行归一化设计,选取优先使用气动舵的控制分配策略,得到了控制量的表达式,在此基础上,采用Backstepping方法,设计了拦截弹俯仰平面内的制导控制律。仿真结果表明,该控制律能够使拦截弹在准确命中机动目标的同时,保持姿态稳定,并且弹道和控制量的变化较平缓,拦截效果理想。
参考文献
YEH Fu-kuang,CHIEN Hsiuan-hau,FU Li-chen.Nonlinear optimal sliding mode midcourse controller with thrust vector control//Proceedings of the American Control Conference.Anchorage,AK:AACC,2002:1 348-1 353.
ORR J S,SLEGERS N J.High-efficiency thrust vector control allocation.Journal of Guidance,Control,and Dynamics,2014,37(2):374-382.
JONSSON H,MALMBERG G.Optimal thrust vector control for vertical launch of tactical missiles.Journal of Guidance,Control,and Dynamics,1982,5(1):17-21.
WILLIAMS D E.Design of an integrated strapdown guidance and control system for a tactical missile,AIAA-83-2169.1983.
XIN M,BALAKRISHNAN S N,OHLMEYER E J.Integrated guidance and control of missiles withθ-Dmethod.IEEE Transations on Control Systems Technology,2006,14(6):981-992.
HUGHES T L,MCFARLAND M B.Integrated missile guidance law and autopilot design using linear optimal control,AIAA-2000-4163.2000.
TOURNES C,WILKERSON P.Integrated terminal guidance and automatic pilot using subspace stabilization,AIAA-2001-4275.2001.
IDAN M,SHIMA T,GOLAN O M.Integrated sliding mode autopilot guidance for dual controlmissiles,AIAA-2005-6455.2005.
[10] SHIMA T,IDAN M,GOLAN O M.Sliding mode control for integrated missile autopilot-guidance,AIAA-2004-4884.2004.
[11] 董飞垚,雷虎民,李炯,等.拦截弹自适应最优滑模制导与控制一体化设计.宇航学报,2013,34(11):1 456-1 461.
DONG Fei-yao,LEI Hu-min,LI Jiong,et al.Design of integrated adaptive optimal sliding-mode guidance and control for interceptor.Journal of Astronautics,2013,34(11):1 456-1 461.(in Chinese)
[12] PALUMBO N F,JACKSON T D.Integrated missile guidance and control:a state dependent Riccati differential equation approach//Proceedings of the 1999 IEEE International Conference on Control Applications.America:IEEE,1999:243-248.
[13] 段广仁,侯明哲,谭峰.基于滑模方法的自适应一体化导引与控制律设计.兵工学报,2010,31(2):191-198.
DUAN Guang-ren,HOU Ming-zhe,TAN Feng.Adaptive integrated guidance and control law design using sliding-mode approach.Acta Armamentarii,2010,31(2):191-198.(in Chinese)
[14] HOU M Z,DUAN G R.Integrated guidance and control for homing missiles against ground fixed targets.Chinese Journal of Aeronautics,2008,21(2):162-168.
[15] MENON P K,OHLMEYER E J.Nonlinear integrated guidance-control laws for homing missiles,AIAA-2001-4160.2001.
[16] 舒燕军,唐硕.轨控式复合控制导弹制导与控制一体化反步设计.宇航学报,2013,34(1):79-85.
SHU Yan-jun,TANG Shuo.Integrated guidance and control backstepping design for blended control missile based on NDO.Journal of Astronautics,2013,34(1):79-85.(in Chinese)
[17] YAN H,JI H.Integrated guidance and control based on backstepping and input-to-state stability.Asian Journal of Control,2011,16(2):654-658.
Integrated Guidance and Control of Interceptor With Thrust Vector Control
HUI Yao-luo1,NAN Ying1,ZOU Jie2
(1.College of Astronautics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;
2.Science and Technology on Electro-optic Control Laboratory,Luoyang 471009,China)
Abstract:Aiming at interceptor with thrust vector control,a method for integrated guidance and control was proposed.Based on the introduction of equivalent elevator angle,multiple-inputs control problem was transformed into a single input problem,and the problem of normalizing the thrust vector and aerodynamic force was resolved.The strategy of control distribution was designed,and expressions of elevator angle and thrust vector deflection angle were given.On the basis of the simplified and standardized model of attack-defense confrontation,integrated guidance and control law was obtained by using backstepping method and Lyapunov redesign method.Numerical simulation results show that the interceptors with this law of integrated guidance and control cannot only get targets effectively,but also make attitudes and the angles of actuators change smoothly compared with conventional method of guidance law and control law designed respectively.
Key words:interceptor;thrust vector control;control distribution;integrated guidance and control;backstepping
中图分类号:V448.2
文献标识码:A
文章编号:1004-499X(2015)04-0001-06
作者简介:惠耀洛(1989- ),男,硕士研究生,研究方向为航天器导航、制导与控制。E-mail:huiyaoluo91@163.com。
基金项目:航空科学基金项目(20140152002);南京航空航天大学研究生创新基地(实验室)开放基金(kfjj201458);中央高校基本科研业务费专项基金项目
收稿日期:2015-08-23

