对经济增长的时间序列和回归分析
赵丽影
对经济增长的时间序列和回归分析
赵丽影

摘要:时间序列分析在经济运用中作用十分明显。本文利用1995—2014年国内生产总值的相关资料,运用时间序列分析,应用Eviews软件对经济增长时间序列进行模型识别、拟合、估计和预测。而改革开放以来,投资在经济增长中的作用越来越明显,在对经济增长序列进行时间序列分析的同时,也结合回归分析建立经济增长和投资的回归模型来分析经济增长和投资的协整关系。
关键词:经济增长;时间序列分析;ARIMA模型;回归模型;投资;协整关系
时间序列数据是计量经济模型的主要数据形式,在实证分析中,许多经济变量是以时间序列的形式出现的,从而时间序列分析在经济运用中作用十分明显。本文通过对经济增长时间序列的时序分析,包括初步识别,拟合模型及模型估计,预测等来简要介绍应用Eviews软件进行时序分析的大致情况。
经济增长是指一个国家或一个地区生产商品和劳务能力的增长。按照库兹涅茨的理解,经济增长不仅指人均国民收入增加,也包括社会制度结构的变化。许多经济学家都提出了各自的经济增长理论,建立了一些经济增长模型。目前对投资与经济增长的关系研究一般认为,投资与经济增长之间存在着正相关关系,即投资的增长会促进经济增长。改革开放以来,投资在经济增长中的作用越来越明显,在对经济增长序列进行时间序列分析的同时,本文也结合回归分析建立经济增长和投资的回归模型来进行分析。
一、数据
本文采用1995—2014年的时间序列数据,数据来源于国家统计局网站。为了进行进一步的统计分析,对数据作了一定的整理:
由于查到的是当年价格计算的数据,为消除物价变动影响,用1995年数据作为不变价格来调整国内生产总值和固定资产投资,即用各年国内生产总值除以各年以1995年为基期的商品零售价格指数,用查到的全社会固定资产投资总额除以各年以1995年为基期的固定资产投资价格指数。结果见表1。
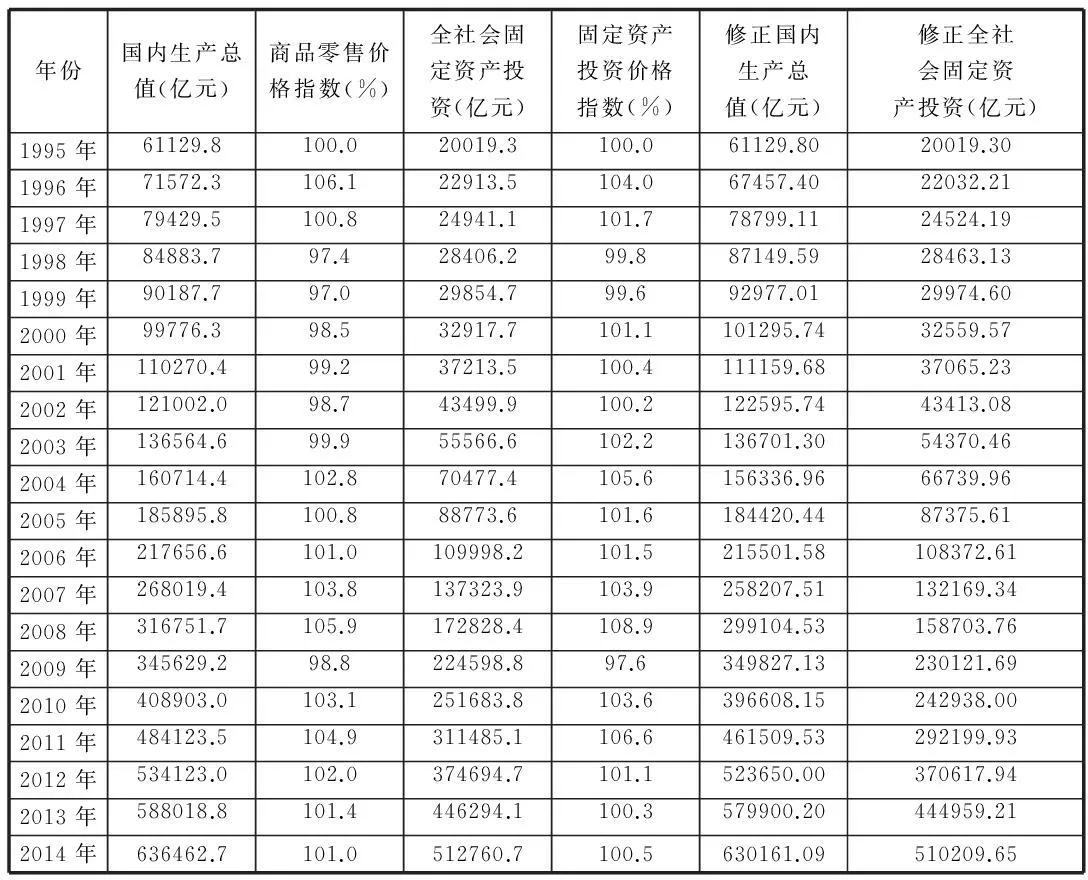
表格1 1995—2014年经济增长数据
数据来源:国家统计局网站
二、方法
(一)ARIMA模型
1.模型建立
(1)数据的平稳性检查。做出1995—2014年修正后的国内生产总值{yt}的时序图,可以看出,该序列大致呈现出指数增长趋势,具有明显的非平稳性。(2)数据的平稳化处理。如果用非平稳序列来建立模型,就会出现虚假回归问题,对于含有指数趋势的时间序列,可以通过对序列取对数来消除指数趋势。绘制取对数后{Inyt}的时序图知取对数后的数据仍然不平稳且具有线性趋势。对于有线性趋势的时间序列我们常常通过差分处理来消除数据的线性趋势。相距一期的两个序列值之间的减法运算称为1阶差分运算。表达式为:▽Inyt=Inyt-Inyt-1,经过1阶差分处理后的{▽Inyt}的时序图显示,序列的平稳性较显著。(3)模型定阶、参数估计、模型检验。利用Eviews软件做出1阶差分后的对数国内生产总值序列{▽Inyt}的自相关图和偏自相关图,如图1。
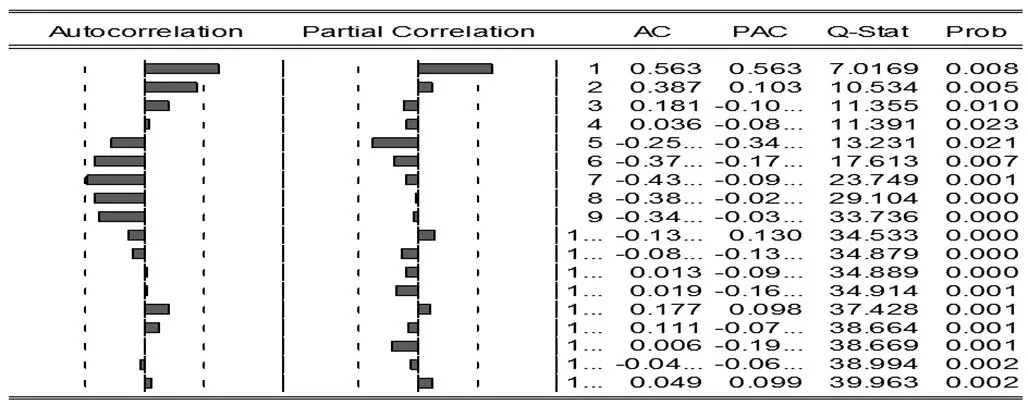
图1 1阶差分后序列的自相关图和偏自相关图
自相关图显示,延迟1阶之后,其他的自相关系数都落入2倍标准差范围以内,而且自相关系数向零衰减的速度非常快,延迟9阶之后自相关系数即在零值附近波动。这是一个非常典型的短期相关的样本自相关图。由时序图和样本自相关图的性质,可以认为该序列平稳,因而采取1阶差分序列{▽Inyt}研究即可。
考虑到自相关系数拖尾,偏自相关系数1阶截尾,所以考虑用AR(1)模型拟合1阶差分后的对数国内生产总值序列{▽Inyt}。考虑到前面已经进行的1阶差分运算,实际上是用ARIMA(1,1,0)模型拟合原序列。利用最小二乘估计,拟合结果为:

对残差序列进行白噪声检验,可以发现,在延迟阶数为6阶和12阶的情况下,Q统计量的值分别为3.036和6.461,P值分别为0.694和0.841。显然,拟合检验统计量的P值都显著大于显著性检验水平0.05,可以认为该残差序列即为白噪声序列。
最小二乘法的结果中,系数显著性检验的结果显示两参数均显著。这说明ARIMA(1,1,0)模型对该序列建模成功。
1.模型拟合。由ARIMA(1,1,0)模型的具体形式可以得到模型的拟合图,如图2。此时的AIC=-4.23374,SC=-4.134809。
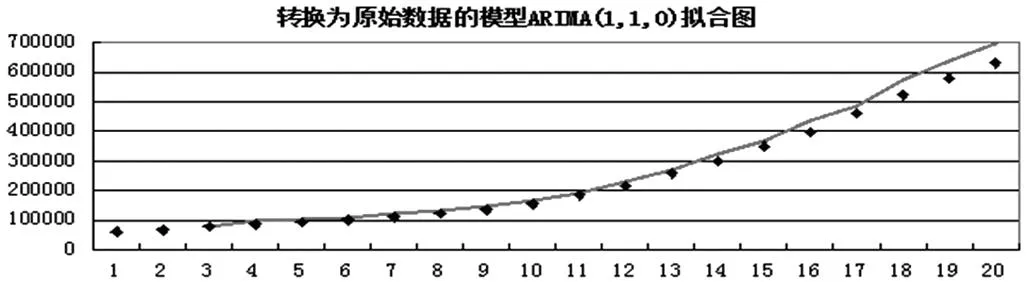
图2 转换为原始数据的模型ARIMA(1,1,0)拟合图
2.模型预测。在拟合模型ARIMA(1,1,0)下,2015年的修正后的国内生产总值为749663.0196亿元。这一预测结果可以与2016年时公布的2015年的国内生产总值数据来进行对比,进而检验模型预测结果的准确性。
(二)关系检验
1.因果关系。分析国内生产总值和全社会固定资产投资之间的因果关系。对两者进行Granger检验,Granger检验的结果显示,在以全社会固定资产投资不是国内生产总值的影响因素为原假设的条件下,P值为0.0058(<0.05),因而有充分的理由拒绝原假设,认为全社会固定资产投资和国内生产总值之间具有因果关系。
2.协整关系。考虑到国内生产总值与全社会固定资产投资之间有逻辑上的因果关系,将全社会固定资产投资作为变量考虑进国内生产总值序列的模型中。协相关图显示,协相关系数几乎全部显著非零,这说明全社会固定资产投资和国内生产总值之间具有回归关系。
由前面的分析我们知道,在没有进行对数和差分转换之前的修正的国内生产总值序列是非平稳的,而修正的全社会固定资产投资序列也是非平稳的,而两者之间又确实具有某种均衡关系,因而可以认为以修正的全社会固定资产投资为自变量的序列{x1},…,{xk}和以修正的国内生产总值为响应变量的序列{yt},两者之间具有协整关系。
(三)回归模型
1.模型建立
(1)先将原数据做对数变换以保证其平稳性和正态性。构造回归模型。利用最小二乘法,构造出的回归模型如下:Inyt=4.203298+0.698784Inxt+εt
(2)残差序列单位根检验。根据残差序列单位根检验结果,P值=0.032(<0.05)可以认为此时的残差序列为平稳的,即{Inxt}和{Inyt}两者之间具有协整关系。对残差序列{εt}进行分析,发现利用中心化的MA(1)模型对其可以进行较好的拟合,拟合结果为:εt=(1+0.600841B)vt。检验结果显示回归模型显著成立,参数显著非零,残差序列{vt}为白噪声序列。
(3)综合的回归模型。由以上的分析可以得出,回归模型为:
Inyt=4.203298+0.698784Inxt+(1+0.600841B)vt
上述的分析说明,尽管国生产总值对数序列{Inyt}和全社会固定资产投资对数序列{Inxt}都是非平稳序列,但是由于他们之间具有协整关系,所以可以建立动态回归模型准确地拟合它们之间的互动关系。
2.模型拟合。由回归模型的具体形式可以得到回归模型的拟合图,如图3。此时的AIC=-3.196445,SC=-3.096872。
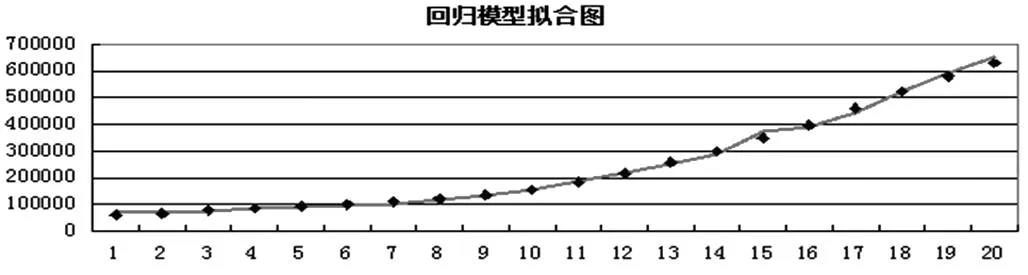
图3 回归模型拟合图
3.模型预测。利用2015年的修正后的全社会固定资产投资额就可以预测出2015年的修正后的国内生产总值。
三、比较
从模型ARIMA(1,1,0)和回归模型的拟合图可以看出,回归模型的拟合图要更好,ARIMA模型的拟合值在后几年普遍要比实际值大,我觉得产生这种差异的原因主要在于:
首先,由前面的分析我们知道,在时间序列的分析中可以选择的模型有很多,不同的模型产生的结果自然不同,这对拟合的精度会产生重要影响,因而要谨慎选择模型。
其次,在建立回归模型的时候,我们对该回归的残差序列建立中心化MA模型,然后将原回归方程的误差项用其中心化MA模型代替。这个模型比单纯的时间序列模型预测效果要好。但同时,回归模型也有着一些缺陷:本文中的回归分析只简单地比较了国内生产总值和固定资产投资之间的关系,由于两者之间很强的相关性,因而使得模型的拟合性很强。但是我们应该注意到,这样的关系在国内生产总值和消费之间也同样存在,因而更加多元的综合分析会更加合理。本文只是简单地设定了国内生产总值和固定资产投资之间是一元的线性关系,模型的简单一定程度上增加了拟合性。
此外,我们也应该看到,尽管回归模型的拟合效果要比ARIMA模型要好,但是ARIMA模型的AIC值和SC值要更小,这说明ARIMA模型在一定程度上要比回归模型更合理。
四、分析
根据中国1995—2014年的国内生产总值数据,我们不难看出,在1995—2000年间,由于1997年亚洲金融危机的影响放缓了中国经济的增长,中国经济始终在低位徘徊,增长速度缓慢。自2000年后中国经济出现了持续快速的增长,但是在2008年世界金融危机的时候国内生产总值有所下降。
影响经济增长的因素很多,包括外部的和内部的,并且这些因素中有相当一部分是不可控的,例如在未来几年内出现大的自然灾害以及出现战争、出现经济危机、通货膨胀等特殊情况。而现实中已经发生的比如:现在投资市场的疯狂,股市大起大落,严重影响了股民的信心,尽管央行以及几大证券公司不断地采取措施救市,但是股市仍在不断地涨停和跌停中风雨飘摇,这也在一定程度上说明了现在中国经济趋于放缓,像国内生产总值这样的综合指标在未来几年仍然会增长,但是增速会下降。在这样的经济形势下,有人就会担心中国经济会不会硬着陆,从我们的分析中可以看出,这样的结果并不会发生,像国内生产总值这样的经济指标的增速是比较稳定的。(作者单位:吉林财经大学经济学院)
参考文献:
[1]于妮莎,王珊珊,《对经济增长的时间序列分析》[J],价值工程,2007年第7期。
[2]李晴,杨春,《时间序列分析模型及其在GDP预测中的应用研究》[J],安徽农业科学,2011年第39卷20期。
[3]严天艳,吕王勇,朱丽萍,《中国人均GDP的时间序列模型的建立与分析》[J],西南民族大学学报·自然科学版,2008年第34卷第6期。
[4]陈娟,余灼萍,《我国居民消费价格指数的短期预测》[J],统计与决策,2005年2月(下)。

作者简介:赵丽影,女,吉林松原人,吉林财经大学数量经济专业硕士研究生。

