例析牛顿第二定律中的突变类问题

周鹏

解决牛顿第二定律的相关问题的关键在于要理解并掌握牛顿第二定律的“四同一相对”的特点，即“同时、同体、同向、同一单位制和相对于惯性系”.其中“同时”是指当合外力改变时，与之相对应的加速度一定是同时改变.因为外力可以突变，所以加速度也存在突变问题.

而对于变化类问题，必须先搞清楚有哪些量瞬时不变，所谓“以不变应万变”.在我们当前的知识背景下，不会突变的物理量有：“速度”和“两端均连有质点的弹簧的弹力”（这主要是因为在“突变”的前提下，变化的时间△t可以认为等于0，从而有△v=a△t=0；弹簧的弹力跟形变量成正比，而形变量改变时，与弹簧相连的质点必须产生相应的位移，也需要时间）.而对于我们常见的轻绳或轻杆而言，一般都是处理成刚体模型，即忽略它们原来的一点点微小的形变，所以它们恢复形变则可以认为不需要时间，也就是说轻绳或轻杆中的弹力可以突变.当然，如果将轻弹簧从中间位置剪断，由于剪断处没有质量，则原来形变的弹簧将产生无限大的加速度，使形变瞬间恢复，所以，一旦弹簧的一端没有质点相连，其弹力也认为可以瞬间减为零.在了解了哪些物理量不能突变后，接下来的处理过程就跟正常用牛顿定律解题时一样了，先进行突变前后的受力分析，找到突变后瞬时的合外力，即可利用牛顿第二定律求得瞬时加速度.下面以几个典型例题加以说明.

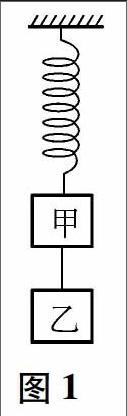
例1 如图1所示，物体甲、乙质量均为m，弹簧和悬线的质量可以忽略不计.当悬线被烧断的瞬间，甲、乙的加速度数值应是下列哪一种情况

（）

A.甲是0，乙是g

B.甲是g，乙是g

C.甲是0，乙是0

D.甲是g/2，乙是g

解析 这是一道最基本的突图1变类问题.悬线被烧断前，弹簧的弹力F弹=2mg，与总重力平衡.悬线被烧断瞬时，两物体所受重力不变，弹簧的弹力不能突变，而悬线的拉力立即变为零，所以，由牛顿第二定律可知：a乙=mg/m=g，向下；a甲=（F弹-mg）/m =g，向上.即选项B正确.

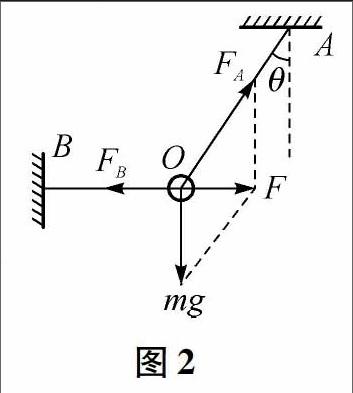
例2 如图2所示，用两根橡皮绳悬挂一质量为m的小球，BO水平，AO与竖直方向成θ角，现将BO剪断，剪断瞬间，小球的加速度是多少？若AO为轻绳，小球的加速度又是多少？

解析 本题最初是上海市的一道高考题，解题的关键在于橡皮绳形变明显，形变需要时间，所以剪断BO的瞬间可认为其形变量和弹力均不发生变化；轻绳形变极小，形变发生变化几乎不需时间，所以剪断BO的瞬间其形变量或弹力均会发生明显变化.

（1）若AO为橡皮绳，剪断BO前，小球受力情况如图2所示.

由平衡条件可得：mg与FA的合力F跟F等值反向，即F=FB=mgtanθ，方向水平向右.

剪断BO瞬间，FB消失，而mg不变，FA亦不能突变，即mg和FA的大小、方向都没有变化，故小球在剪断BO瞬时所受的合外力与剪断BO前完全相同.所以由牛顿第二定律得：a=F/m=gtanθ，方向水平向右.这也就意味着小球在一个极短的时间内将先沿水平方向加速运动，然后因FA减小而逐渐向下偏.

（2）若AO为轻绳，则在剪断BO的瞬时，不仅FB消失，并且FA的大小也要瞬间发生变化，此时我们就无法再根据剪断前的受力寻找剪断后的合力，所以应改变思路，在剪断后小球的运动情况上找突破口.

因为剪断BO后，小球沿圆弧左右摆动，A点为圆心，O点是摆动的最高点，所以可知剪断BO后，小球的瞬时加速度沿O点的切线方向向下.

剪断OB瞬时，在最高点O，小球的重力沿AO方向的分力mgcos0与此时刻的FA相互平衡（此时无速度，不需要向心力，所以沿AO方向小球受力平衡），重力沿O点切线方向的分力mgsinθ就成了小球的合外力.

由牛顿第二定律可得：a=F合/m=gsinθ，方向沿O点切线方向向右下方.

可见，这里需要注意的是：瞬时性问题的处理思路一般有两个方向：若除突变因素本身外无其他力发生突变，可根据原来的稳定状态分析瞬间状态；若除突变因素本身外还有其他力发生突变，只能通过后来的运动过程推测瞬间状态.

在以上两例中，质点的受力情况和运动情况都比较明确，相对而言也容易处理，在有些情况下，物体的受力情况并不明确，还需要先进行假设和讨论.

例3 如图3所示，木块A、B用轻弹簧相连，放在用细绳悬挂的木箱C内，都处于静止状态，它们的质量分别为m、2m和3m.当剪断细绳的瞬间，求各物体的加速度大小及其方向？

解析从系统的自由端开始分析.对木块A，在细绳剪断前受重力和弹簧的弹力而平衡，在细绳剪断后瞬间重力不变，而弹簧的弹力又不能突变，所以仍受力平衡，从而aA=0.

本题的难点在于木块B、C在细绳剪断后的受力和运动情况分析，因为直观上较难判断B、C在细绳剪断后是否会分开.所以，在这里要先作一个假设，假设B、C在细绳剪断后会分开，即剪断后FBC=0.（当然，也可以假设不会分开，即剪断后FBC>0）

由假设可知，剪断后FC合=mc9= mcac，得ac=g，方向竖直向下；

FB合=mBG+F弹=mAg+mBg=3mg=2maB，得aB=1.5g，方向竖直向下；

而B、C分开的条件是ac>aB，这与上述结果矛盾，所以以上假设不成立.也就是说，细绳剪断后，B、C不会分开，而是作为一个整体一起向下加速运动.

则对B、C整体，受总重力mBg+mc9=5mg和弹簧的压力F弹=mAg=mg，即FBc合=6mg，由牛顿第二定律得，加速度：aB=aC=FBC合/5m=1.2g.

这个结果才是合理的，因为B、C间存在弹力，所以木块B的加速度1.2g应当比B单独运动时的加速度1.5g要小，而木块C的加速度1.2g应当比C单独运动时的加速度g要大.