高延性混凝土单轴受压本构模型研究

邓明科，潘姣姣，秦 萌,2，刘海勃

(1．西安建筑科技大学土木工程学院，陕西 西安710055；2．成都天华西南建筑设计有限公司，四川 成都610016)

高延性水泥基复合材料[1-4](engineered cementitious composite，ECC)是一种具有高强度、高韧性和高耐损伤能力的新型材料，在拉伸和剪切荷载下表现出良好的多裂缝开展和应变硬化特性，可显著提高混凝土材料的韧性和耐损伤能力，在土木工程领域具有广泛的应用前景．为便于ECC在混凝土结构中的应用，本课题组采用ECC设计理论制备了高延性混凝土(high ductile concrete，HDC)，并对其进行了受压、受弯与受拉力学性能的试验研究[5-8]，但是对高延性混凝土的单轴受压应力-应变关系仍需进一步的研究．

混凝土单轴受压本构关系是研究结构构件承载力和变形能力的主要依据，对于构件的弹塑性全过程分析和结构延性设计均具有重要的意义．李艳等通过单轴受压试验，得到了高韧性PVA-FRCC单轴受压本构方程[9]；焦楚杰等通过试验得出了钢纤维高强混凝土单轴压缩本构方程[10]；徐世烺等研究了超高韧性水泥基复合材料的单轴受压应力-应变全曲线和非线性分析模型[11]．前期研究表明[12]，与普通混凝土相比，高延性混凝土单轴受压时，基体内部的纤维桥联作用，使试件纵向受压时受到稳定的横向约束力，其抗压韧性和受压变形能力明显提高，因此，高延性混凝土的单轴受压本构模型与普通混凝土有较大区别．

本文选取尺寸为100 mm×100 mm×300 mm的棱柱体试件，进行高延性混凝土单轴受压试验，并考虑纤维掺量、粉煤灰掺量、水胶比和砂胶比对应力-应变曲线形状及其特征点的影响，提出适用于高延性混凝土的单轴受压本构模型，为高延性混凝土结构设计和非线性数值模拟提供了理论依据．

1 试验概况

试验采用的高延性混凝土基本组成为：水泥(P·O 42.5R)、I级粉煤灰、泾阳天然河砂(最大粒径为1.18mm)、矿物掺合料、PVA纤维和水．PVA纤维的具体参数见表1，试验配合比设计见表2，其中配合比1为不含纤维的水泥砂浆基体对比试件．

表1 PVA纤维性能指标Tab.1 Properties of PVA fiber

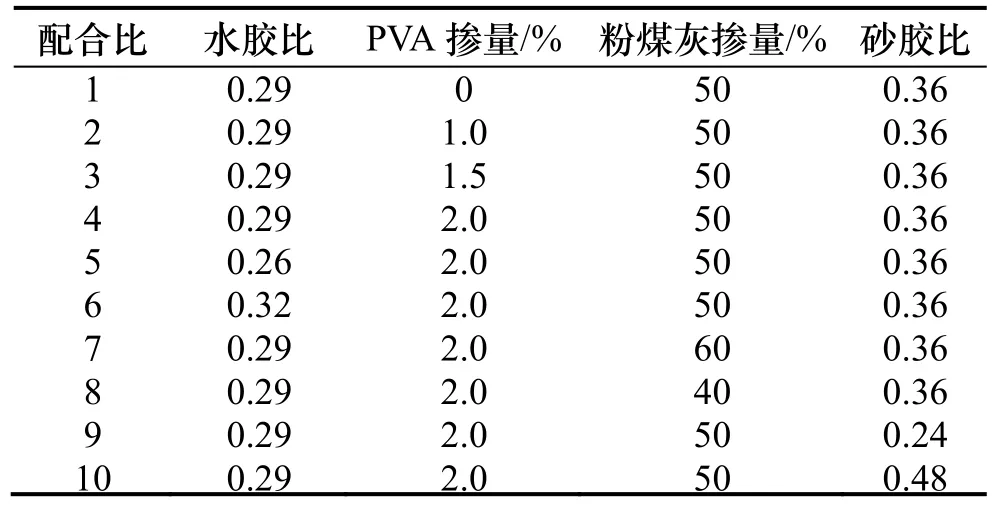
表2 试验配合比设计Tab.2 Mix design for experimental program

2 试验结果分析

2.1 试件破坏形态

砂浆基体的受压破坏过程与混凝土类似，试件达到峰值荷载以后发生崩裂，并立即丧失承载力，发生明显的脆性破坏．

高延性混凝土试件纵向受压时，横向产生拉伸变形．试件的上、下端因受到加载垫板的约束而横向变形较小，中部虽受到加载垫板的约束力很小，但受到基体内部纤维桥联应力的约束作用明显．由于 HDC良好的拉伸应变硬化性能，试件中部的横向拉伸变形始终可以受到纤维桥联应力的有效约束，使基体内部纵向裂缝的出现和扩展明显滞后．直到试件横向拉伸变形超过了 HDC的极限拉应变时，基体内部的纤维被拔出或拉断，试件中部受到的横向约束力失效，在最薄弱处出现纵向裂缝并上下贯通形成一条主裂缝．试件破坏过程中，主斜裂缝两侧试块发生明显错动，试件承载力基本保持不变．由于纤维的桥联作用，试件受压破坏以后仍保持一定的剩余承载力和较好的完整性．试件纵向受压的裂缝分布及破坏形态如图1所示．

图1 HDC试件裂缝分布及破坏形态Fig.1 Crack distribution and failure mode of HDC specimens

2.2 单轴受压应力-应变曲线

试验测得各组试件单轴受压的应力-应变曲线如图2所示．从图2中可以看出，本次试验测得的高延性混凝土单轴受压破坏过程和应力-应变曲线具有以下特点：

加载初期，曲线上升段的应力-应变基本保持为线弹性关系，斜率基本保持不变；当应力达到抗压强度的80%左右时，纤维提供的横向约束力达到最大值，由于内部裂缝的扩展，应变增长速度加快，使应力-应变曲线斜率减小；试件达到峰值荷载时，纤维提供的横向约束力失效，试件中部裂缝迅速扩展并向上下两端延伸，荷载迅速降低；当应力下降至峰值荷载的 10%～20%，应力-应变曲线下降段出现一个拐点(曲率最大点)，之后曲线趋于平缓．

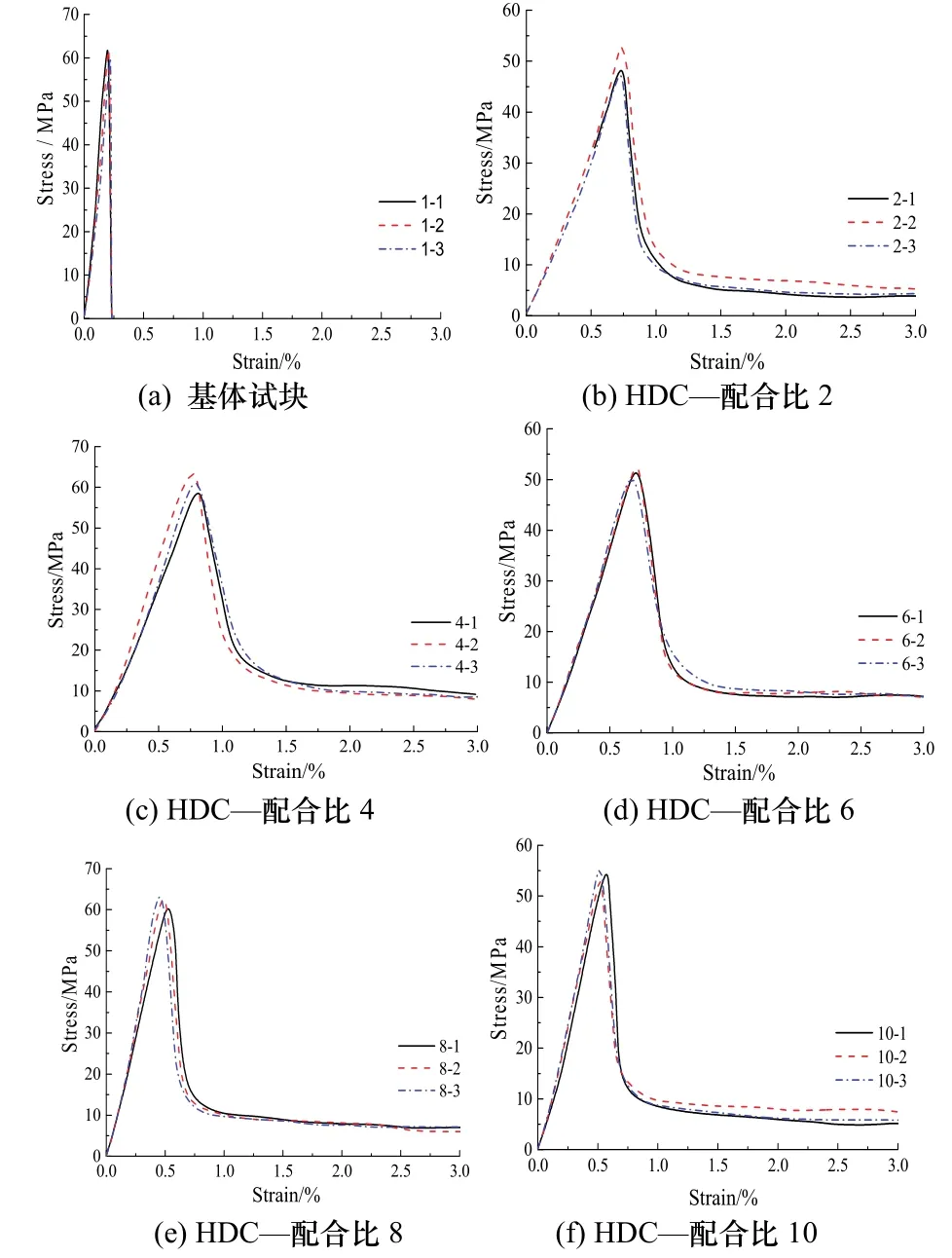
图2 HDC单轴受压应力-应变曲线Fig.2 Uniaxial compression stress-strain curves of HDC

2.3 单轴受压应力-应变曲线特征点

表 3给出了各组试件应力-应变曲线的特征点及其对应的应力和应变值．由图2和表3可以看出，砂浆基体(配合比1)对应的峰值应变为0.002 1，与《混凝土结构设计规范》[15]相应混凝土的峰值应变接近．高延性混凝土的峰值变形较砂浆基体试件均有明显提高，9组不同配合比HDC的峰值应变可达砂浆基体的2.61～3.15倍，表明HDC达到峰值荷载以前的变形能力得到明显提高，具有约束混凝土受 力特点．

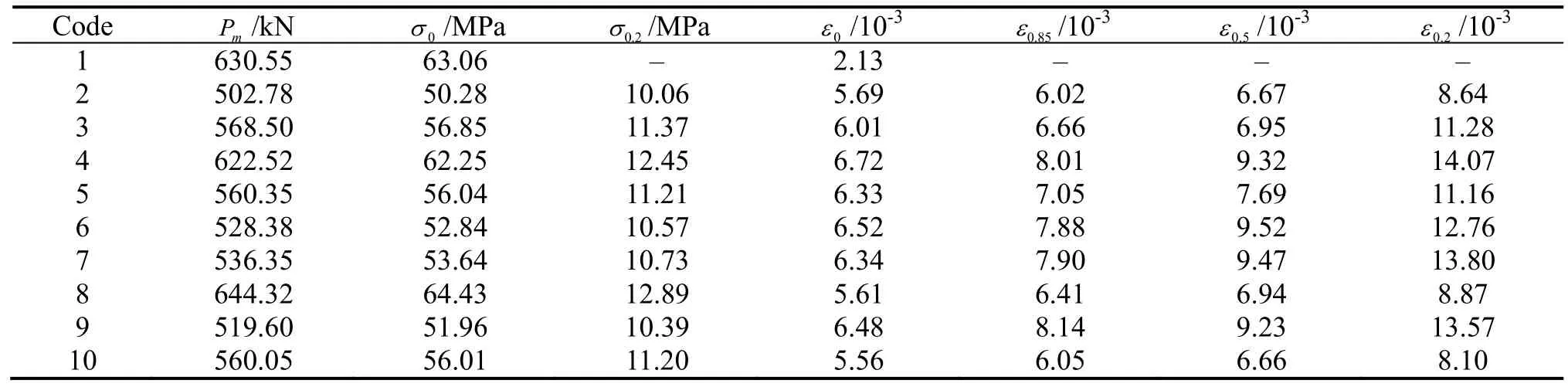
表3 HDC受压本构模型参数Tab.3 Parameters of HDC compression constitutive model

图3 各因素对受压应力-应变曲线各特征值的影响Fig.3 Influence of various factors on characteristic value of compression stress-strain curves

2.4 各因素对应力-应变曲线特征点的影响分析

根据表3的试验结果，可得纤维掺量、水胶比、粉煤灰掺量和砂胶比四种因素对 HDC单轴受压应力-应变曲线特征点应变值的影响如图3．对各因素的影响分析如下：

(1) 纤维掺量

高延性混凝土基体内部乱向分布的短纤维能有效阻止内部微裂缝的产生和发展，提高了试件单轴受压的变形能力．由表3和图3(a)分析可得，随着纤维掺量的增加，高延性混凝土应力-应变曲线的峰值应变提高不明显，但极限压应变均有明显提高．当纤维掺量由1%增加到2%时，ε0.85、ε0.5和ε0.2分别提高了33.06%、39.73%和62.85%．

(2) 水胶比

水胶比减小，拌合物的和易性降低，导致基体内部纤维分散不均匀，使得纤维的增韧和阻裂作用减弱．由图3(b)可以看出，水胶比为0.26的试件极限压应变比水胶比为0.29和0.32的试件均有所降低．由于本次试验中水胶比的变化范围较小，水胶比对试件单轴受压变形能力的影响较小．

(3) 粉煤灰掺量

由表3和图3(c)可以看出，当粉煤灰掺量由40%增加至50%时，试件的峰值应变和极限压应变均有明显提高，这是因为粉煤灰可以改善纤维与基体之间的界面特性，有助于发挥纤维的增韧作用，在一定程度上提高试件的受压变形能力．但粉煤灰掺量过高，试件抗压强度有所降低．

(4) 砂胶比

砂胶比由0.24增加至0.36时，试件变形能力提高并不明显；增大至0.48时，高延性混凝土的抗压强度有所提高，但纤维与基体之间的摩擦力增大，使得纤维大多被拔断，在一定程度上降低了材料的拉伸变形能力，导致其受压变形能力降低．因此，砂胶比过高，试件单轴受压的极限压应变明显降低．

3 单轴受压本构关系

3.1 单轴受压应力-应变曲线

图4 HDC单轴受压无量纲应力-应变曲线Fig.4 Uniaxial compression dimensionless stress-strain curves of HDC

从图4可大致看出HDC应力-应变曲线的特点：其走向规律与混凝土相似，由上升段和下降段组成；曲线上升段斜率单调下降；在峰值应力点，曲线斜率降为零；曲线下降段，先出现一个拐点，接着出现曲率最大点，然后曲线趋于平缓．

根据以上分析，结合参考文献[14]，高延性混凝土的应力-应变曲线应满足以下条件：

3.2 本构模型的确定

基于高延性混凝土单轴受压应力-应变曲线的形状及其特点，可采用以下三种模型：

(1) 过镇海建议的分段式曲线方程[14]：

(2) Sargin建议的有理分式曲线方程[13]：

根据条件⑥，③下降段应力-应变曲线可表示为：

(3) Saenz建议的有理分式曲线方程[13]：

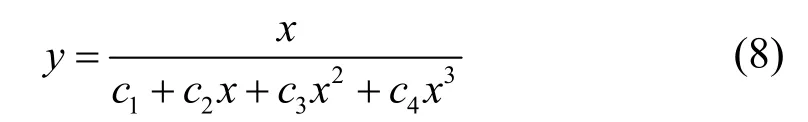
因此上升段应力-应变曲线可表示为：

上述三种模型的上升段和下降段在曲线峰值点连续，并符合上述全部几何特征(①～⑦)的要求．为了便于对比和分析三种模型，统一将上升段曲线方程中的参数设为aα，下降段曲线方程中的参数设为dα，二者均具有相应物理意义[14]．

上升段参数aα为初始弹性模量(E0)与峰值割线模量(Eg)的比值；下降段参数当y≡1，峰值点后为水平线(全塑性)；当dα=∞时，y≡0，峰值点后为垂直线(脆性)．

根据条件②，可推出三种模型中参数aα的取值范围．经过推导与代换，三种模型的曲线方程及其参数取值范围如下：

(1) 过镇海建议的分段式曲线方程(模型1)：

(2) Sargin建议的有理分式曲线方程(模型2)：

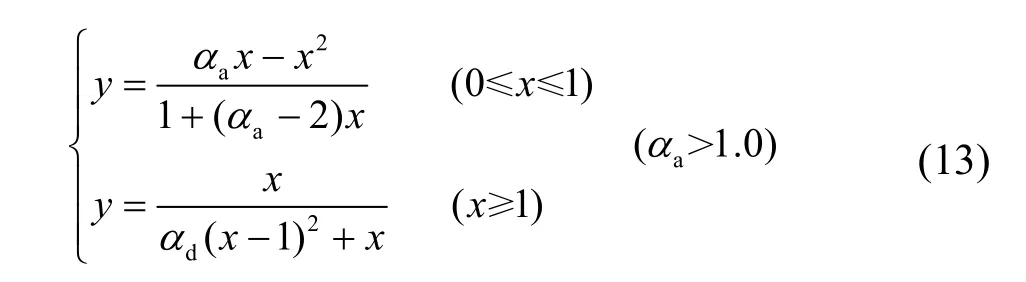
(3) Saenz建议的有理分式曲线方程(模型3)：

可见，三种模型的应力-应变曲线上升段方程有所差异，下降段均采用同一方程．

3.3 本构模型参数的确定

与普通混凝土相比，HDC的单轴受压应力-应变曲线具有以下特性：

(1) 纤维的横向约束作用，使试件弹性段明显变长，达到峰值应力80%以前均接近线性，纵向裂缝的产生和发展滞后．

(2) 基体内部的纤维桥联作用，使HDC的峰值应变明显提高，具有约束混凝土的受力性能．

(3) 达到峰值荷载以后，纤维的横向约束作用失效，曲线下降段更陡峭．

(4) 试件破坏以后仍具有一定的残余强度，曲线下降段出现拐点．

因此，高延性混凝土单轴受压应力-应变曲线的上升段参数aα和下降段参数dα与普通混凝土应有所不同．

基于上述分析，依据最小二乘法，对高延性混凝土单轴受压应力-应变曲线进行非线性回归，得到三种模型的参数及其相关系数如表4所示．由曲线参数的物理意义可知，上升段参数aα越大，峰值应力与弹性极限应力的差值越大，下降段参数dα越小，曲线下降越平缓．

由表4可见，模型1的上升段参数aα与试验结果相差较大，其相关系数明显小于模型 2和模型3．考虑配合比设计中各因素变化的影响，对模型2和模型3上升段参数和下降段参数进行如下分析：

随着纤维掺量的增加，单轴受压应力-应变曲线上升段参数aα逐渐增大，下降段参数dα逐渐减小，表现为曲线的上升段和下降段均逐渐趋于平缓，曲线下方所包含的面积逐渐增大，说明纤维掺量增大，试件受压破坏过程中吸收的能量增加，试件的抗压韧性提高．水胶比减小，aα逐渐减小，dα逐渐增大，表现为曲线的上升段和下降段逐渐陡峭，曲线下方所包含的面积有所减小，试件的抗压韧性有所降低．粉煤灰掺量增大以及砂胶比减小，aα逐渐增大，dα逐渐减小，曲线下包的面积有所增大，试件的抗压韧性提高．

以上三种本构模型的无量纲应力-应变曲线与HDC受压试验曲线对比如图5所示．通过对比表4中的相关系数和图5中的曲线可以发现：采用模型2和模型3得到的拟合曲线与试验曲线吻合较好，其中模型2最接近于试验曲线．

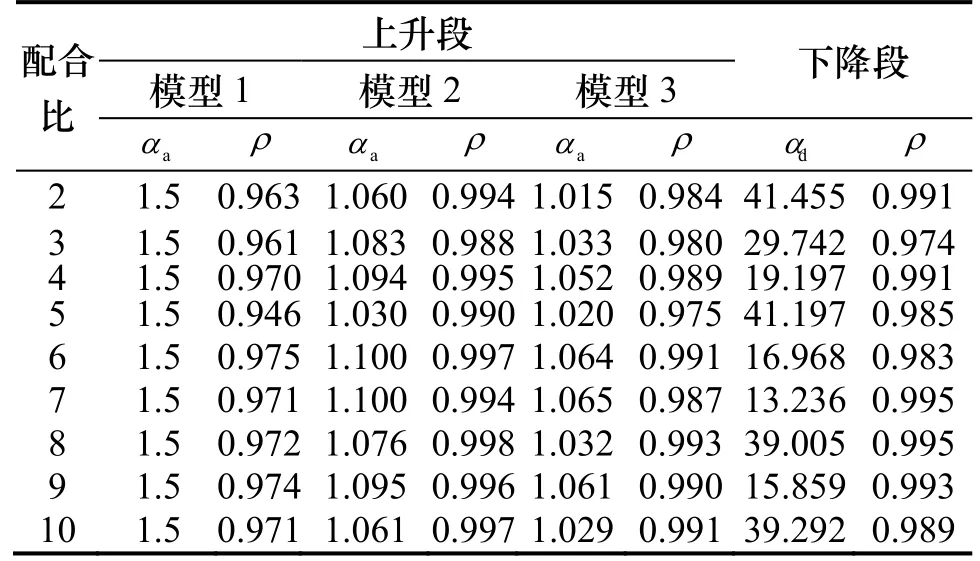
表4 HDC应力-应变曲线参数Tab.4 Parameters of HDC stress-strain curve

图5 实测应力-应变全曲线与本构模型的对比Fig.5 Comparison between stress-strain curve and constitutive model

4 结论

(1) 高延性混凝土试件单轴受压时，试件中部受到基体内部纤维桥联应力的约束作用，纵向裂缝的产生和发展滞后，试件破坏以后始终具有10～20%的剩余承载力和较好的完整性，表现出较高的抗压韧性．

(2) 纤维掺量、粉煤灰掺量和砂胶比对HDC单轴受压应力-应变曲线的特征点均有一定的影响．纤维掺量增大，HDC的极限压应变明显提高；粉煤灰掺量增加，HDC的峰值应变和极限压应变均有明显提高，但抗压强度有所降低；砂胶比增大，HDC的抗压强度有所提高，但极限压应变明显降低．

(3) 与普通混凝土相比，HDC单轴受压应力-应变曲线的弹性段明显变长，峰值应变明显提高，曲线下降段更陡峭并出现明显拐点，其上升段参数aα和下降段参数dα也有所不同．

(4) 依据最小二乘法，对三种HDC单轴受压本构模型上升段参数和相关系数进行分析发现，采用模型2和模型3得到的拟合曲线与试验曲线吻合较好，其中模型2最接近于试验曲线．

References

[1] LI V C, LEUNG C K Y. Steady state and multiple cracking of short random fiber composites [J]. Journal of Engineering Mechanics, ASCE, 1992, 188(11): 2246-2264.

[2] LI V C. ECC–tailored composites through micromechanical modeling[C]//Fiber Reinforced Concrete: Present and the Future. Montreal: Canadian Society of Civil Engineering, 1998: 64-97.

[3] LI V C. On engineered cementitious composites (ECC): a review of the material and its applications [J]. Journal of Advanced Concrete Technology, 2003, 1(3): 215-230.

[4] LI V C, WANG S, WU C. Tensile strain-hardening behavior of PVA-ECC [J].ACI Materials Journal,2001,98(6): 483- 492 .

[5] 邓明科, 孙宏哲, 梁兴文, 等. 延性纤维混凝土抗弯性能的试验研究[J]. 工业建筑, 2014, 44(5): 85-90.DENG Mingke , SUN Hongzhe, LIANG Xingwen, et al.Experimental study of flexural behavior of high ductile fiber reinforced concrete [J]. Industrial Construction,2014, 44(5):85-90.

[6] 邓明科, 孙宏哲, 梁兴文, 等. 延性纤维混凝土抗压与抗弯性能研究[J]. 工业建筑, 2014, 44(10): 115-121.DENG Mingke, SUN Hongzhe, LIANG Xingwen, et al.Experimental study of compressive behavior and flexural behavior of high ductile fiber reinforced concrete [J].Industrial Construction, 2014, 44(10): 115-121.

[7] 邓明科, 秦萌, 梁兴文. 高延性混凝土抗压性能试验研究[J]. 工业建筑, 2015, 45(4) : 120-126.DENG Mingke, QIN Meng, LIANG Xingwen. Experimental study of compressive behavior of engineered cementitious composities[J]. Industrial Construction,2015, 45(4): 120 -126.

[8] 寇佳亮, 邓明科, 梁兴文. 延性纤维增强混凝土单轴拉伸性能试验研究[J]. 建筑结构, 2013, 43(1): 59-64.KOU Jialiang, DENG Mingke, LIANG Xingwen. Experimental study of uniaxial tensile properties of high ductile fiber reinforced concrete [J]. Building Structure,2013, 43(1): 59-64.

[9] 李艳,刘泽军. 高韧性PVA-FRCC单轴受压力学性能及本构关系[J].建筑材料学报, 2014,17(4): 606-612.LI Yan, LIU Zejun. The uniaxial compressive mechanical properties and constitutive relation of high toughness PVA–FRCC.[J]. Journal of Building Structures,2014,17(4): 606-612 .

[10] 焦楚杰, 孙伟, 秦鸿根, 等. 钢纤维高强混凝土单轴受压本构方程[J]. 东南大学学报(自然科学版),2004,34(3): 366-369.JIAO Chujie, SUN Wei, QIN Honggen, et al. The uniaxial compression constitutive equation of steel fiber reinforced high strength concrete [J]. Journal of Southeast University (Natural Science Edition),2004,34(3):366-369.

[11] 徐世烺, 蔡向荣, 张英华. 超高韧性水泥基复合材料单轴受压应力-应变全曲线试验测定与分析[J].土木工程学报,2009,42(11): 79-85.XU Shilang, CAI Xiangrong, ZHANG Yinghua. Experimental measurement and analysis of the axial compressive stress-strain curve of Ultra High Toughness Cementitious Composities[J]. China Civil Engineering Journal, 2009, 42(11): 79-85.

[12] 邓明科,刘海勃,秦萌,等. 高延性纤维混凝土抗压韧性试验研究[J].西安建筑科技大学学报(自然科学版),2015,47(5):660-665, 677.DENG Mingke, LIU Haibo, QIN Meng, et al. Experimental study research on compressive toughness of the high ductile fiber reinforced concrete[J].J. of Xi’an Univ.of Arch. & Tech.(Natural Science Edition), 2015,47(5):660-665,677.

[13] 过镇海.混凝土的强度和变形(试验基础和本构关系)[M]. 北京: 清华大学出版社,1997.GUO Zhenhai.The strength and deformation of concrete(experimental basis and constitutive relation), principle and application [M]. Beijing: Tsinghua University Press,1997.

[14] 过镇海,时旭东.钢筋混凝土原理和分析[M]. 北京: 清华大学出版社,2003.GUO Zhenhai, SHI Xudong. Reinforced concrete theory and analyse[M]. Beijing: Tsinghua University Press,2003.

[15] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010-2010 [S]. 北京: 中国建筑工业出版社.Ministry of Housing and Urban-Rural Development of People's Republic of China. Code for design of concrete structures: GB 50010-2010[S]. Beijing: China Building Industry Press.