建筑钢板件力磁效应的ANSYS有限元模拟研究
苏三庆,高 波,王 威,易术春,马小平
(西安建筑科技大学土木工程学院,陕西 西安 710055)
钢材在建筑钢结构、桥梁钢结构及大跨空间钢结构等土木工程领域得到广泛使用,钢结构的节点等关键部位在服役过程中承受各种动载或交变荷载作用,容易造成局部应力集中和微观缺陷拓展,这可能导致构件在低于材料屈服强度情况下发生突发性的断裂,及时找出结构断裂前的危险区域对这些大型工程项目尤为重要.目前,常规的无损检测方法存在只能检测出已成形的宏观缺陷的弊端,在实际工程应用中具有一定的局限性;而金属磁记忆检测技术作为一门新兴的无损检测方法[1-2],它不需要外磁场的激励,而以地磁场为背景磁场,通过测量应力引起的残余漏磁场,即可对铁磁材料的应力集中程度和损伤等实现早期检测诊断,解决了上述问题,所以,金属磁记忆检测技术有望在建筑钢结构等工程中的早期健康检测得到广泛应用[3-5].
现阶段金属磁记忆检测方法的研究主要集中在探索性实验和理论模型建立等方面,例如,任吉林等对 20#钢进行了不同程度的拉伸试验,测量了卸载后的试件表面漏磁场信号,指出磁记忆信号的变化与材料内部微观组织的状态密切相关[6];基于经典Jiles-Artherton理论模型,冷建成等对Q235低碳钢做了拉伸试验,提出了考虑塑性变形影响的改进模型[7],通过对45#钢扭转试验,徐明秀等验证了扭转材料的改进Jiles-Atherton模型,拓展了该模型的应用范围[8];杨理践等采用密度泛函理论的平面波赝势法,计算了晶体磁性能随力的定量变化关系,并对金属磁记忆效应中的力-磁耦合关系做出定量分析[9].但是目前缺乏相关数值模拟的研究,姚凯[10]等假设铁磁材料的应力和磁导率之间满足线性关系,仅分析了一定应力水平下提离值等对漏磁信号幅值的变化趋势,未做定量化分析.
因此,通过对建筑钢结构广泛使用的Q345B钢的人工浅槽拉伸试件进行二维平面有限元数值模拟,根据应力表征铁磁材料磁参数(磁导率)的力磁效应关系式,分析不同应力状态下空气中法向漏磁信号B(y)及其梯度的分布规律,最后通过试验验证模拟结果.
1 基本原理
1.1 麦克斯韦方程组
麦克斯韦方程组是经典电磁理论的基础,它可以解决任何宏观电磁现象和电磁过程.金属磁记忆检测是以地磁场为背景磁场,对给定地理位置座标的空间来说,可以认为地磁场强度值保持恒定不变.当铁磁构件处于无电流源域时,其无源稳态磁场的麦克斯韦方程组为
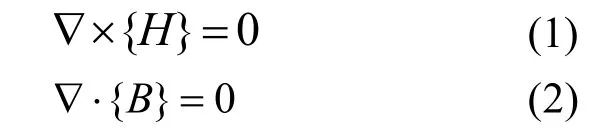
式中:{B}为磁感应强度矢量,{H}磁场强度矢量.
为提高电磁场数值计算的效率,引入矢量磁位函数(磁矢势){A}来减少求解的自由度数,此磁矢势满足

从上述(1)~(3)式可推得:

对二维平面模型,对于磁矢势{A}有
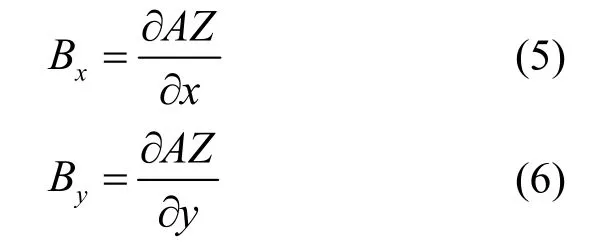
式中,AZ表示磁矢势{A}在Z方向的分量,它是电磁方程计算中的唯一变量.
1.2 力磁关系式
文献[11]根据磁介质磁化理论分析计算,得到了反映铁磁材料力磁效应的函数关系式

从该方程可以推导如下方程式
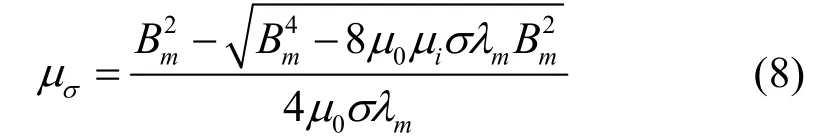
式中:真空磁导率μ0=4π×10-7H/m,Q345B为低碳钢,其饱和磁感应强度Bm=2.5 T,饱和磁滞伸缩系数λm=5×10-6,初始相对磁导率μi=260,μσ为应力不为零时计算得到的相对磁导率.
2 模拟过程
模拟由静力学分析和静磁学分析两阶段组成.静力学采用线性强化弹塑性模型分析得到钢板拉伸荷载下的应力分布结果,将此结果保存在单元表中;在静磁学分析中,调用储存在单元表中的应力分布结果来修改铁磁材料的相对磁导率,以此来模拟应力对铁磁材料磁学属性的影响[12].
图1给出了Q345B钢试件的尺寸模型,在试件中部的两侧预先设置对称分布的人工浅槽以模拟应力集中,浅槽大小为l×b=1 mm×3 mm,试件厚δ=10 mm,检测线分布在槽口附近,长度为60 mm,检测点等间距分布.
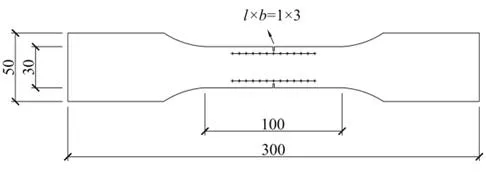
图1 试件尺寸Fig.1 Size of specimen
2.1 建立模型
静力学和静磁学分析时,都采用相同单元划分的试件尺寸模型,为考虑应力集中的影响,对缺陷所在区域的网格细化.静磁学分析时还应在试件模型外部添加空气模型,以采集试件外表面空气中的漏磁信号.建立的试件尺寸模型如图2所示.
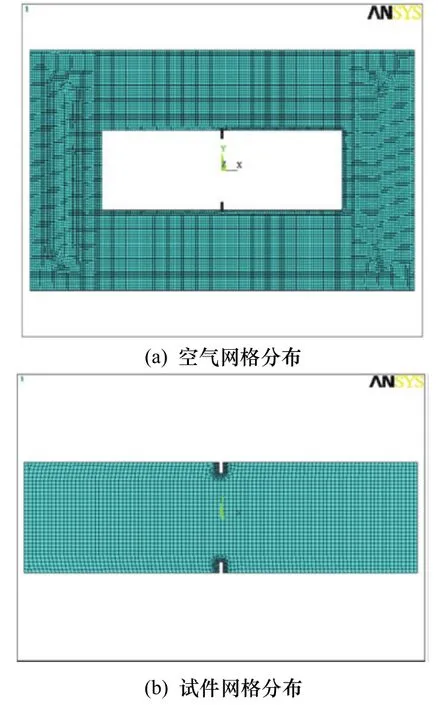
图2 单元网格划分Fig.2 Meshing of finite element model
划分网格的单元大小设置为 1 mm,在缺陷处包含一层网格加密区,图2(a)为外层空气模型,图2(b)为内层试件模型,单元总计15 154个.
2.2 加载和求解
静力学分析中,对模型一端施加全部位移约束,另一端施加均匀拉力的线载荷,建好模型后,端面的约束和载荷会自动传递到单元的节点上.为了使模拟结果和实验结果具有可比性,荷载的加载等级与实验结果一致.
在地磁场环境下进行二维平面静磁学分析时,除了试件模型外,其外侧还有一层空气模型,对于空气模型的外边界需施加通量垂直边界条件[13].根据力磁关系式(8)可求得不同应力水平下铁磁材料的磁导率,铁磁材料单元的磁学属性赋值以后,便可得到该模型在地磁场下施加拉力载荷后铁磁材料的表面漏磁场分布情况,并将计算所得的磁场强度法向分量保存起来.因为计算的单元数量很多,模拟时通过ANSYS参数化语言将材料的磁学属性赋值给单元,并保存计算得到的漏磁分布结果.
3 模拟结果分析
3.1 应力的分布规律
试验前对Q345B钢板拉伸测试发现,当试件拉伸到110 kN时,在试件中部出现非常明显的颈缩现象,此时颈缩对试件内部磁畴结构的影响加剧[6],不适于用应力表征磁信号的变化规律,因此不考虑110 kN以后试件拉伸作用下磁信号的变化情况.
图3(a)展示了试件在85 kN拉伸荷载作用下的应力云图,从中可以看出,应力幅值的最大值出现在缺口的内侧,缺口外边缘处应力幅值最小,并且缺口处应力云图呈现“鱼尾”状分布.图3(b)给出了试件名义屈服前后,沿着试件长度方向缺口部位的应力分布情况,越靠近缺陷位置,应力幅值越大,应力集中程度越高,图中出现的双峰现象与应力云图分布规律吻合,X坐标轴中间位置的应力幅值与计算得到的缺陷处名义应力值一致.

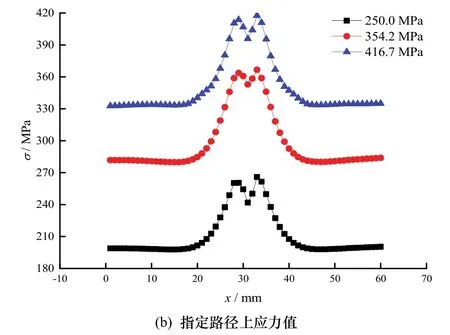
图3 槽口处应力集中分布Fig.3 Stress concentration of pits in specimen
3.2 磁信号的分布规律
由金属磁记忆检测法的原理[14]可知,在轴向拉伸应力作用下铁磁体内部的磁畴组织发生了定向和不可逆的重新取向,从而导致应力或应变集中区域表面的漏磁场发生变化.当拉应力增加时,铁磁性材料中磁畴的磁矩方向趋向一致,最终在应力或应变集中处积聚大量磁化能形成较强的漏磁场,表现为法向分量B(y)过零点,梯度值K出现极值.图4分别表示弹、塑性阶段应力集中区磁感应强度B(y)和其梯度值K随应力的变化规律.

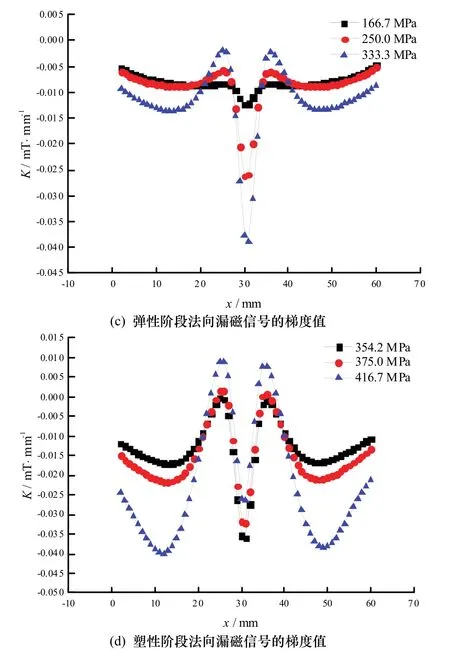
图4 有限元模拟的弹、塑性阶段法向漏磁信号及其梯度值的分布Fig.4 Normal component with its gradient of MFL value at elastic & plastic stage of the modeling
分析图 4(a)和图 4(c)可以看出,宏观上,弹性阶段试件表面的磁信号曲线形貌相近,其大小分布与载荷强度存在正相关关系,与磁信号法向分量的分布图过坐标轴原点呈中心对称不同,梯度值左右两侧的分布关于x轴的中线呈轴对称。细观上,进一步观察可见,磁信号法向分量的绝对值随载荷增加而增大,其大小在应力σ=333.3 MPa时比σ=166.7 MPa时增大近一倍,达到0.4 mT。同时,梯度的幅值也随载荷增加而增大,在缺陷处梯度值的变化幅度明显,在x轴中点处出现极值,为−0.04 mT/mm。此外,在试件中部即x=30 mm处,磁信号法向分量始终过零点,不受载荷大小的变化而发生位置改变,这些与理论分析的结果符合.进入塑性阶段后,试件缺陷处名义应力从σ=354.2 MPa增大到σ=416.7 MPa,从图4(b)和图4(d)中可以看出,应力集中区域的磁信号的变化比弹性阶段更剧烈,磁信号法向分量及其梯度值的曲线发展趋势保持一致,但幅值变化显著.需要指出的是,塑性阶段缺陷附近处磁信号法向分量及其梯度值的分布范围沿试件长度方向伸长,这与弹性阶段变化稍有区别,因为塑变对试件的磁畴的影响加剧,造成试件表面的漏磁场强度在缺陷处出现波动,非线性变化趋势增强.
基于上述分析可知,磁感应强度变化较好地反映了弹性阶段磁记忆信号随应力集中程度的分布规律,在试件屈服后,塑变引起的磁畴结构变化显著,虽然对用应力表征磁记忆信号造成干扰,但可利用弹性阶段和塑性阶段磁信号变化迥异的特点,实现应力集中程度及损伤状态的早期识别.
4 试验结果验证
试验材料选用广泛应用的Q345B钢,考虑退火处理后试件内部组织结构的变化会造成试件磁导率相应的改变,以及考虑到实际工程情况,因此未对试件进行高温退火处理.试验中采用在线测量方法,实验前在试件的检测范围内画好检测线,检测点间距为5 mm,采集数据时,沿着画好的检测线依次逐点在线测量试件表面漏磁场法向分量B(y)值,保持探头垂直紧贴于试件表面,测量时应远离强磁场的干扰.拉伸试验在WAW-2000D电液伺服万能试验机上进行,磁记忆信号检测设备选用高精度WT10B 型数字高斯计,最大量程为200 mT,分辨率为0.01 mT.
对浅槽试件进行轴向拉伸测试时,发现浅槽试件分别加载到85 kN 和110 kN时发生屈服和出现明显的颈缩现象.由于颈缩会干扰应力和磁记忆信号间的变化规律,因此对颈缩不予考虑,细化后浅槽试件的加载等级为:0、20、40、60、80、85、90、100 kN.
图5(a)和(c)、图5(b)和(d)分别表示拉伸荷载下试件弹性、塑性阶段应力集中程度对法向磁感应强度B(y)和其梯度值K的影响规律[5].
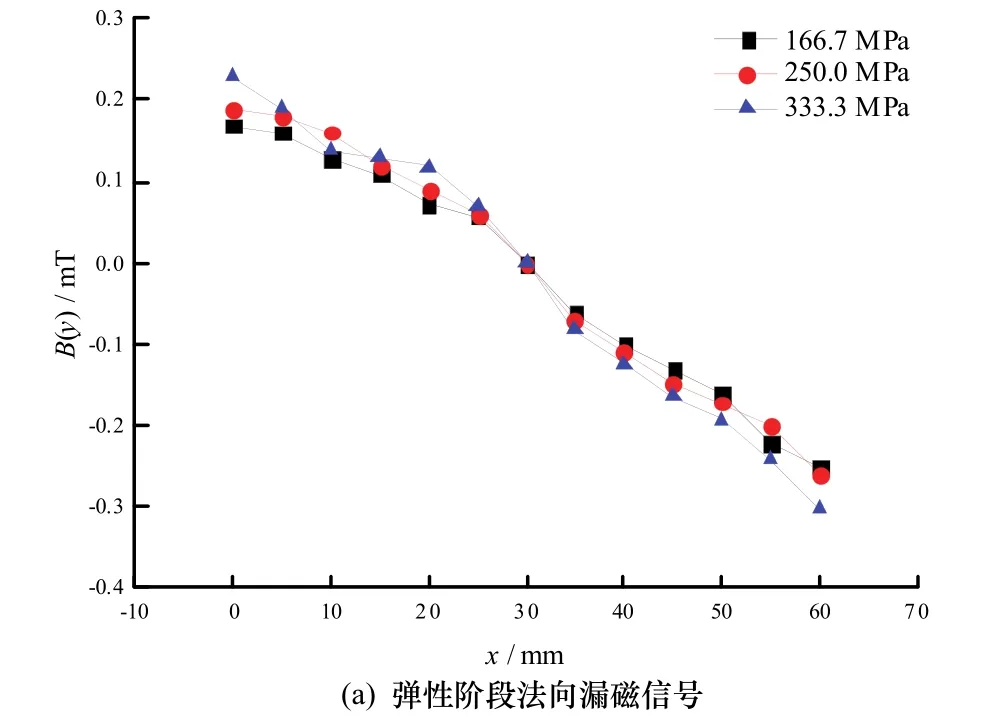

图5 试验的弹、塑性阶段法向漏磁信号及其梯度值的分布Fig.5 Normal component with its gradient of MFL value at elastic & plastic stage of the experiment
由图5可知,随着拉应力的增加,磁场强度的绝对值随之增大,磁场强度的梯度值也随之增大,在试件中间位置磁场强度值B(y)过零点,磁场强度的梯度值K出现最大值。模拟得到的结果在试件缺陷处有明显的上下波动现象,而在试验中未观察到此现象,一方面与试验时信号采集点密度以及仪器分辨率等因素有关,另一方面试验时试件两侧端部夹持产生的漏磁场也会影响检测准确度,这两方面是造成试验中捕捉到的磁记忆信号与模拟的结果在缺陷处略有区别的主要因素.总体上,模拟的计算结果和试验数据的变化趋势相符合,漏磁场分布区域及幅值范围相差不大,证实了模拟结果的可靠性,本文有限元模型可用于建筑中钢板件的拉伸磁记忆有限元分析.
5 结论
(1) 根据已知的力磁效应表征函数,对 Q345B建筑钢板件进行了有限元建模分析,得出不同受力阶段应力集中对铁磁构件磁记忆信号的变化规律,可为工程早期损伤的识别提供参考.
(2) 有限元模拟结果较好反映了弹性阶段磁信号与应力间的变化规律,进入塑性阶段以后,应变的较快增长对用应力来表征磁信号变化造成干扰,但可根据弹塑性阶段磁信号变化迥异的特点,实现损伤早期发现.
(3) 通过模拟得到的漏磁场分布区域、幅值分布范围与实验结果相吻合,该数值模拟方法可用于建筑中钢板件的拉伸磁记忆有限元分析.
References
[1] DUBOV A A. Development of a metal magnetic memory method[J]. Chemical & Petroleum Engineering, 2012,47:837-839.
[2] WU Dabo, XU Minqiang, LI Jianwei. Study on physical mechanism of metal magnetic memory technique[J].Applied Mechanics & Materials, 2010, 34-35:841-844.
[3] WANG Wei, YI Shuchun, SU Sanqing. Experimental investigation of stress and damage characterization of steel beam buckling using magnetic memory signals[J].Structural Design of Tall & Special Buildings, 2016,25(11):508-518.
[4] 王威, 曾发荣, 苏三庆, 等. 基于磁记忆的受弯钢梁力-磁效应试验[J].材料科学与工程学报,2016,34(1):109-114.WANG Wei, ZENG Farong, SU Sanqing, et al.Experimental research on magnetic mechanical effectiveness of bending steel beam based on metal magnetic memory[J]. Materials Science & Engineering,2016,34 (1):109-114.
[5] 王威, 易术春, 苏三庆, 等. 建筑钢试件拉伸应力与其磁记忆效应漏磁场梯度的对应关系研究[J].西安建筑科技大学学报(自然科学版),2015,47(3):341-346.WANG Wei, YI Shuchun, SU Sanqing, et al. Research on the relationship between magnetic flux leakage gradient by metal magnetic memory effect and tensile stress of building steel specimen[J]. J. Xiʹan Univ. of Arch. & Tech.(Natural Science Edition), 2015,47(3):341-346.
[6] 任吉林, 王东升, 宋凯, 等. 应力状态对磁记忆信号的影响[J]. 航空学报,2007, 28(3): 724-728.REN Jilin, WANG Dongsheng, SONG Kai, et al.Influence of stress state on magnetic memory signal[J].Acta Aeron Nautical Et Astronautica Sinica, 2007,28(3):724-728.
[7] LENG Jiancheng, LIU Yang, ZHOU Guoqiang, et al.Metal magnetic memory signal response to plastic deformation of low carbon steel[J]. Ndt & E International,2013, 55(3):42-46.
[8] XU Mingxiu, XU Minqiang, LI Jianwei et al. Metal magnetic memory field characterization at early fatigue damage based on modified Jiles-Atherton model[J].Journal of Central South University, 2012,19(6):1488-1496.
[9] 杨理践, 刘斌, 高松巍,等. 金属磁记忆效应的第一性原理计算与实验研究[J].物理学报,2013,62(8):086201-086207.YANG Lijian, LIU Bin, GAO Songwei, et al.First-principles calculation and experimental study of metal magnetic memory effects[J]. Acta Physica Sinica,2013, 62(8): 086201-086207.
[10] 姚凯,王正道,邓博,等. 金属磁记忆技术的数值研究[J].工程力学,2011(9):218-222.YAO Kai, WANG Zhengdao, DENG Bo, et al. Numerical study on metal magnetic memory technique[J]. Engineering Mechanics,2011,28(9):218-222.
[11] 王社良, 王威, 苏三庆, 等. 铁磁材料相对磁导率变化与应力关系的磁力学模型[J].西安科技大学学报,2005,25(3):288-291.WANG Sheliang, WANG Wei, SU Sanqing, et al.Magneto-mechanical model on differential permeability and stress of ferromagnetic material[J].Journal of Xiʹan University of Science and Technology, 2005,25(3):288-291.
[12] 阎照文.ANSYS10.0工程电磁分析技术与实例详解[M].北京:中国水利水电出版社,2006.YAN Zhaowen.ANSYS10.0Engineering electromagnetic analysis technique and detailed examples[M]. Beijing:China Water Resources and Hydropower Publishing House, 2006.
[13] 胡仁喜. ANSYS13.0多物理耦合场有限元分析从入门到精通[M]. 北京:机械工业出版社,2012.HU Renxi. ANSYS 13.0 multi-physics coupling finite element analysis (From entry to the master)[M]. Beijing:Mechanical Industry Press, 2012.
[14] 任吉林, 林俊明, 池永滨, 等. 金属磁记忆检测技术[M]. 北京: 中国电力出版社,2000.REN Jilin, LIN Junming, CHI Yongbin, etal. Metal magnetic memory testing technology[M]. Beijing: China Electric Power Press,2000.

