新型自复位方钢管混凝土框架的抗侧刚度研究
王先铁,刘立达,周绪红,贺 博,郑江
(1.西安建筑科技大学土木工程学院,陕西 西安710055;2.重庆大学土木工程学院,重庆 400030)
我国现阶段的抗震思想是“小震不坏,中震可修,大震不倒”[1].目前,“小震不坏和大震不倒”已经可以做到,但是对于“中震可修”的实现缺乏具体做法.震后会因为主体结构发生较大的塑性变形而导致结构维修费用和时间增加,有些结构甚至无法完全修复而不能继续使用[2].近年来,以减小建筑结构震后残留变形为目标、有效控制结构最大变形的自复位结构,逐渐成为国内外研究的热点.
20世纪90年代初,自复位结构概念首先在美国的PRESSS研究计划中被提出[3],其技术核心为通过引入后张拉预应力使结构具有自复位能力,从而解决结构的残余变形问题.梁柱自复位节点是自复位结构的关键组件之一.美国里海大学的J.Ricles等[4]首先将自复位节点应用于钢框架结构,并对 8个十字型梁柱自复位节点进行了试验研究.结果表明,后张拉自复位节点具有优异的弹性刚度、强度及延性,节点初始弹性刚度可达到全焊接节点,未出现明显的残余变形.Garlock等[5-6]研究了初始预应力大小、预应力束等对自复位节点性能的影响.结果表明,自复位节点具有很好的耗能性能和延性.Midorikawa等[7]对自复位预应力钢框架进行了三向模拟地震振动台试验研究.结果表明,自复位钢框架上部结构的变形等于或略小于柱脚刚接钢框架弹性阶段的变形.在国内,潘振华等[8]对 4个自复位钢框架节点的低周反复荷载试验表明,梁、柱在整个加载过程中保持弹性,塑性变形主要集中在节点角钢处.蒋成良等[9]采用有限元软件ANSYS研究了钢绞线预应力大小对自复位钢框架性能的影响.张艳霞等[10]对3个腹板摩擦耗能的钢框架自复位节点研究表明,梁柱等主要构件基本处于弹性,残余转角很小,实现了自复位目标.
综上所述,目前的自复位节点大多为绕梁翼缘转动节点,且柱子基本为H型钢.但由于后张拉梁柱节点对节点区强度和刚度有较高要求,因此,钢框架自复位节点构造复杂,易产生预应力损失.方钢管混凝土柱比型钢柱具有更高的强度和刚度,且具有良好的经济性、施工性能及建筑适用性.将方钢管混凝土框架与自复位梁柱节点结合即可形成自复位方钢管混凝土框架.本文提出了一种新型绕梁腹板销轴转动的自复位方钢管混凝土框架节点,推导了自复位方钢管混凝土框架的抗侧刚度计算公式,并通过有限元软件 ABAQUS建模分析,验证了刚度计算公式的合理性,分析了钢绞线面积和初始预应力大小对框架自复位性能的影响,研究了自复位框架的失效机制并给出初始预应力建议值.
1 新型自复位框架梁柱连接节点
新型自复位方钢管混凝土框架梁柱连接节点如图1所示.预应力钢绞线一端锚固于方钢管柱壁外侧的端板,另一端锚固于与钢梁腹板和翼缘焊接连接的锚固板,方钢管混凝土柱内置套管,以利于钢绞线贯通,预应力钢绞线沿梁腹板中线对称分布.该节点可有效避免以往自复位框架梁柱节点易出现的“梁增长”[11]现象.

图1 自复位节点构造形式Fig.1 Detail of self-centering connection
自复位节点转动时,梁翼缘与柱壁保持分离,上下相对位置处的钢绞线受力不同.以节点向右侧转动为例,下层钢绞线处于拉伸状态,其应力值将增大;上层钢绞线处于松弛状态,其应力值将会减小.理想情况下,上层钢绞线应力增量与下层钢绞线应力减小值相同.钢绞线拉伸和松弛形成一对力偶,为结构提供恢复力.从能量角度看,结构恢复力为借助结构弹性势能的释放和重力势能的转换来实现,即利用结构自身吸收地震能量的释放以获得恢复力,从而减小结构的残余位移[12].
2 新型自复位方钢管混凝土框架抗侧刚度计算公式
对于图1所示自复位节点,发生转动时,钢绞线中的预应力将发生变化.设较大内力为P1,较小内力为P2,初始内力为P0,且钢绞线选用同一种材料和直径.则

式中:APT为钢绞线截面面积;EPT为钢绞线弹性模量;LPT为钢绞线长度;Δ为节点转动时,钢绞线的变形量;ϕ为结构侧移角;y为钢绞线距梁中线的距离;Δ损失为节点转动过程中中梁受压产生的变形.
对于单个自复位节点,钢绞线内力对梁中线弯矩为
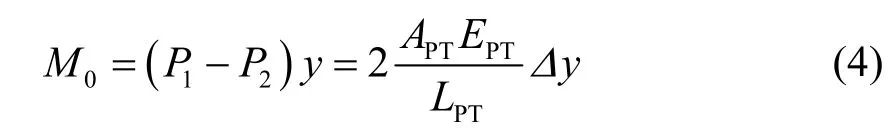
对于单层自复位框架(图2).当发生单位转角时,由虚功原理,有
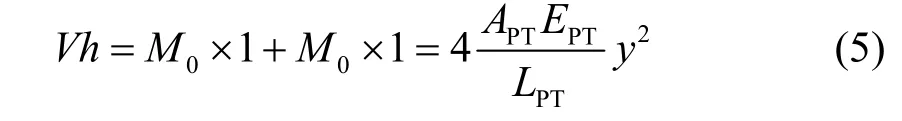
则单层自复位框架的侧向刚度为

同理,对于n层自复位框架,有
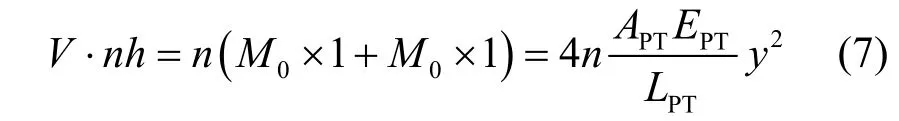
则其对应的侧向刚度为

由公式(6)可知,自复位框架侧向刚度与钢绞线材料属性、钢绞线截面面积及其布置位置等有关,与框架梁、柱等构件截面无关.公式(6)、(8)成立的条件为钢绞线处于受拉状态且未达到屈服应力.
为保证自复位框架节点转动性能,以钢绞线达到最大应力为极限状态,梁柱截面强度应满足

式中:MC,MB分别为框架柱和框架梁按截面边缘屈服为极限状态确定的抗弯承载力设计值;M0′为极限状态下,自复位节点转动产生的弯矩.
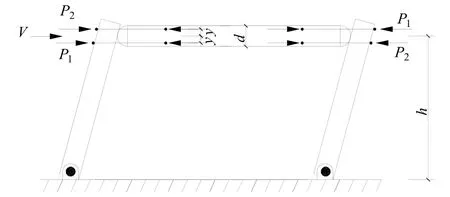
图2 单层自复位框架Fig.2 Single-storey self-centering frame
3 抗侧刚度计算公式有限元验证及参数分析
3.1 模型建立
采用有限元软件ABAQUS对自复位框架抗侧刚度计算公式进行验证.分别建立单跨单层和单跨三层1:3模型,跨度2 300 mm,层高1 300 mm.通过改变关键参数研究自复位框架抗侧刚度与各参数之间的关系,并检验抗侧刚度计算公式的正确性.根据文献[13]和公式(9)确定模型主要构件尺寸.方钢管截面为□400×12,内灌C40混凝土,钢梁截面为H300×150×10×12.销轴直径为 30 mm.通过改变钢绞线面积和初始预应力,研究其对自复位框架抗侧刚度的影响,钢绞线沿梁高方向间距 200 mm,钢绞线有效长度为1 090 mm.梁柱钢材屈服强度fy=345 MPa,弹性模量E=2.06×105MPa,强化模量取为0.02E,泊松比ν=0.3.钢绞线的弹性模量EPT=1.95×105MPa,抗拉强度标准值fy1=1 865 MPa.预应力通过降温法施加,具体计算方法为

式中:Δt为需要施加的温度值;ε为钢绞线对应的应变值;α为钢绞线的线膨胀系数,取1.25×10-5/℃;T0为钢绞线预拉力;EPT为钢绞线的弹性模量;APT为钢绞线截面面积.
钢材均选用壳单元(S4R),钢绞线选用杆单元(T3D2),销轴和钢管内混凝土选用实体单元(C3D8R).考虑构件的几何、材料及接触非线性.混凝土采用塑性损伤模型,其塑性参数取值[14]如表1所示.
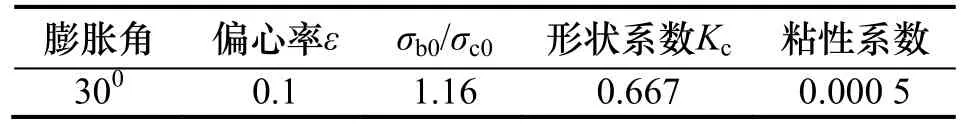
表1 混凝土材料塑性参数Tab.1 Plastic coefficients of concrete
方钢管与混凝土之间的接触关系法向定义为“硬”接触,切向采用库伦摩擦模型,摩擦系数取0.6.销轴与钢板预留孔面接触关系为法向定义为“硬”接触,切向采用库伦摩擦模型,摩擦系数为0.3.为防止结构发生面外变形,对顶梁和中梁上翼缘施加面外约束.方钢管混凝土柱脚采用铰接.按位移控制加载方法在柱顶施加位移荷载,取极限位移角为2%.有限元模型及网格划分如图3所示.各模型钢绞线面积及预拉力大小如表2、表3所示.
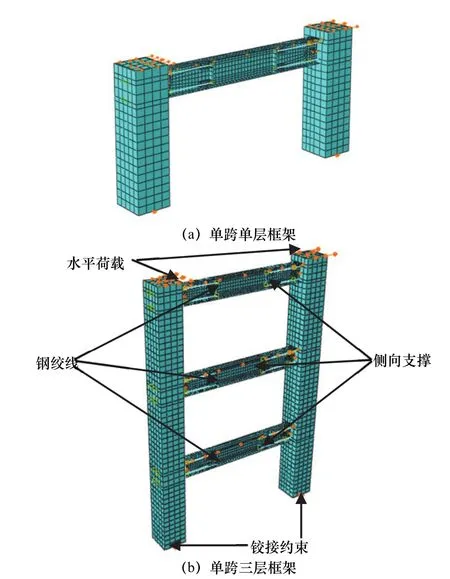
图3 框架有限元模型Fig.3 Finite element models of frame

表2 各模型钢绞线面积Tab.2 Section areas of strands in each models

表3 各模型钢绞线预应力Tab.3 Pre-stress of strands in each models
3.2 结果分析
对上述模型进行往复加载,设层高为h,以h/400为初始加载位移,之后以初始位移的整数倍循环加载,直至加载位移为h/50[13].有限元分析得到的各模型荷载-位移曲线如图4所示.
由图 4可知,自复位框架在循环荷载作用下,荷载-位移呈线性关系,荷载-位移曲线为过原点的直线,残余位移很小,具有很好的自复位能力.因本文自复位框架中未设置耗能构件,侧向荷载作用下框架始终保持弹性,因此自复位框架没有耗能能力.由图4(a)、(c)可知,随着钢绞线截面面积的增大,自复位框架侧向刚度和承载力增大;由图4(b)、(d)可知,当钢绞线截面面积不变时,随着初始预应力的增大,自复位框架侧向刚度几乎不变,说明当框架和钢绞线处于弹性时,初始预应力大小对自复位框架侧向刚度影响很小,和公式(6)、(8)与初始预应力无关一致,初步验证了公式的合理性.
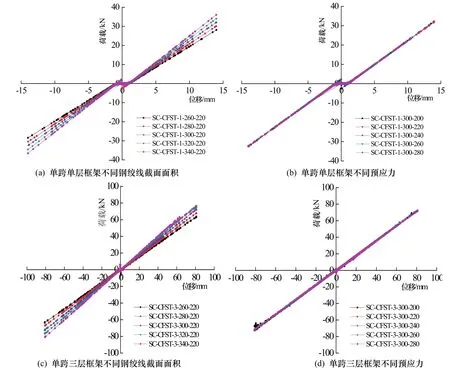
图4 各模型荷载-位移曲线Fig.4 Load-displacement curves of models
由图4可得不同钢绞线截面面积时自复位框架的侧向刚度,并与公式(6)、(8)得到的侧向刚度理论值进行对比,如表4所示.由表4可知,随着钢绞线截面面积增大,自复位框架的侧向刚度逐渐增大.单层自复位框架理论刚度略大于有限元分析刚度;三层自复位框架理论刚度小于有限元分析刚度.对于单层自复位框架,随着钢绞线截面面积增大,理论刚度值与有限元分析刚度值误差逐渐增大.对于三层自复位框架,随着钢绞线截面面积增大,误差逐渐减小.因此,对于单层自复位框架,当钢绞线截面面积较小时,理论值与有限元值吻合较好;对于多层自复位框架,当钢绞线截面面积较大时,理论值与有限元值吻合较好.由表 4可知, 公式(6)、(8)具有较好的精度.
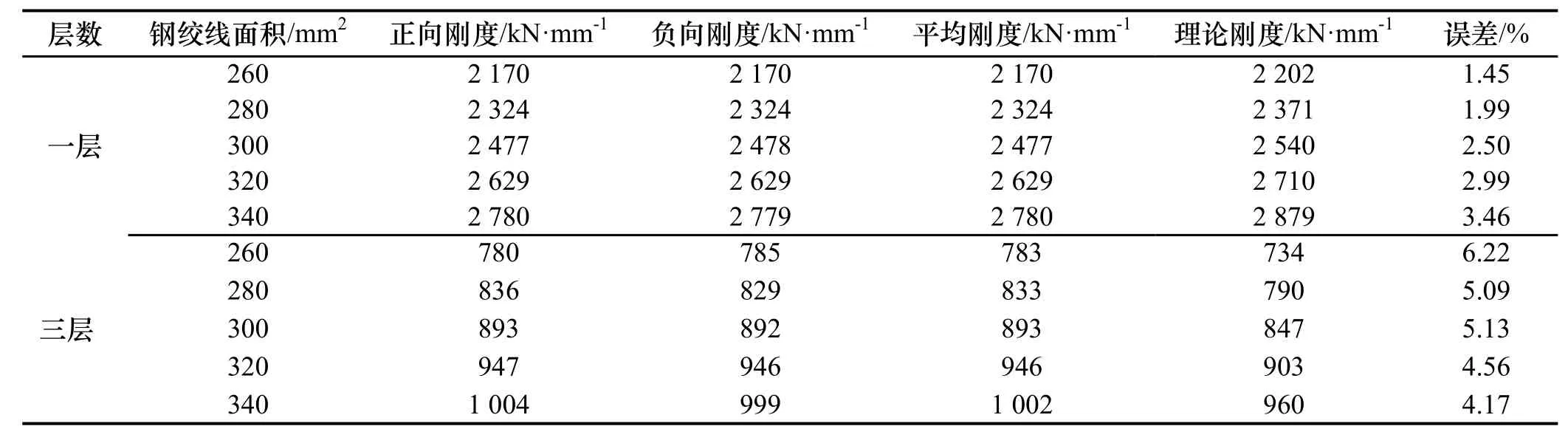
表4 公式与有限元刚度值对比Tab.4 Comparison of theory stiffness and finite element analysis
4 失效机制分析
对于自复位框架结构,需保证钢绞线始终处于弹性状态,才能保证框架具有自复位能力.为研究自复位框架结构的失效机制,对上述三层框架模型进行有限元分析.取钢绞线截面面积为300 mm2,极限位移角为4%,初始预拉力分别取100 kN、220 kN、370 kN,分别对应模型1、模型2、模型3.有限元分析得到的荷载-位移关系如图5所示,极限位移时(2%层间位移角)对应von Mises应力如图6所示.
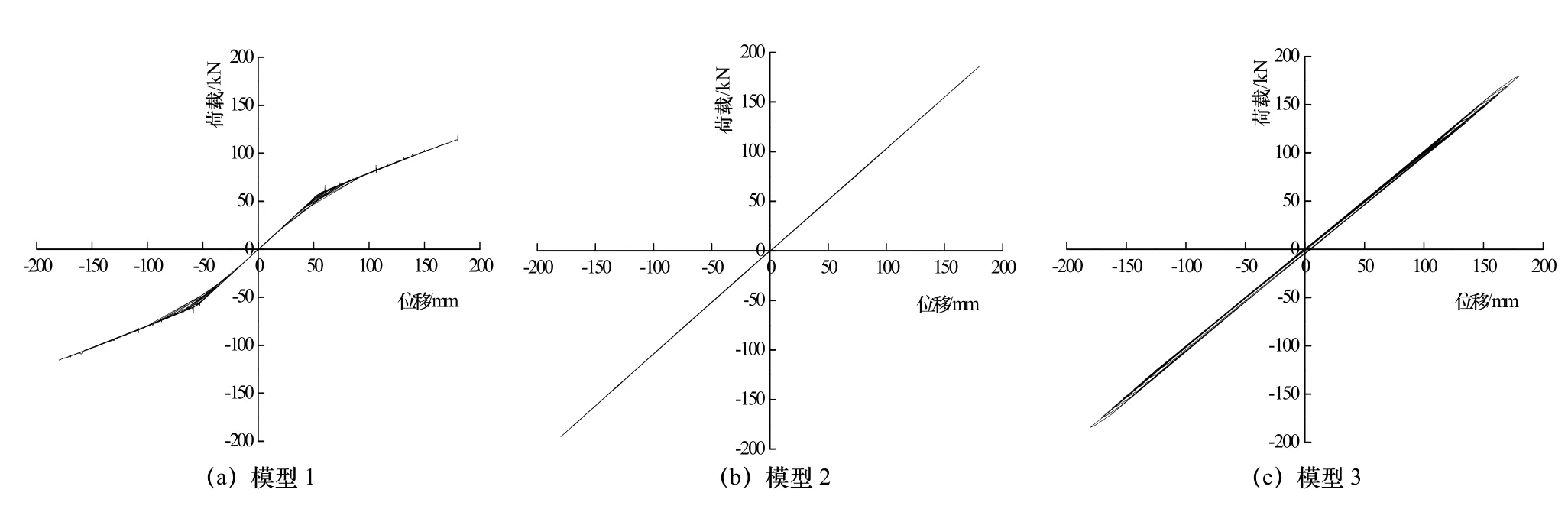
图5 不同模型的荷载-位移曲线Fig.5 Load-displacement curves of models

图6 von Mises应力Fig.6 von Mises stress
由图5可知,加载初期,三个模型的荷载-位移曲线与预应力参数分析结果一致,框架刚度相同;加载后期,模型1的荷载-位移曲线出现明显偏折,框架刚度减小,承载力增长缓慢.结合图6可知,模型1中钢绞线最大应力为1 064 MPa,钢绞线最小应力为零,框架恢复力机制发生改变,即由钢绞线力偶提供恢复力转变为单根钢绞线提供恢复力,框架刚度降低,与图5(a)中荷载-位移曲线的变化对应.模型2的荷载-位移曲线为直线,框架具有良好的自复位能力,为理想的自复位框架结构.模型 3的荷载-位移曲线出现较小的滞回环,与模型 2相比,模型3的荷载-位移曲线存在残余变形,且当加载到每周循环目标位移时,框架刚度值有减小的趋势.结合图6和钢绞线应力分布可知,钢绞线最大应力已达到其抗拉强度.因钢绞线达到抗拉强度后将无法提供恢复力,且随着位移的增大,框架刚度逐渐减小,结构将失去自复位能力.因有限元软件本构关系的限制,钢绞线达到抗拉强度后可再次回到弹性阶段,不能反应钢绞线屈服即失效的性能.因此,图5(c)未能明显地显示自复位性能的减弱和刚度退化.但是,通过有限元分析,探明了自复位框架的失效机制及失效的原因.
由以上分析可知,自复位框架存在两种失效机制,分别为一侧钢绞线应力减小为零或一侧钢绞线达到抗拉强度.因此,初始预应力取值不能过大或过小.已知目标侧移时,需提前确定初始预应力大小,预防上述两种失效机制的发生,保证自复位框架结构具有良好的自复位能力.
5 初始预应力取值
为保证自复位框架在允许侧移内处于弹性阶段,且具有良好的自复位能力,应合理确定钢绞线初始预应力值.取层间位移角限值为 1/50[1],即ϕ=2%.为避免自复位框架失效,钢绞线初始预应力需满足以下条件:

则初始预应力取值范围为:
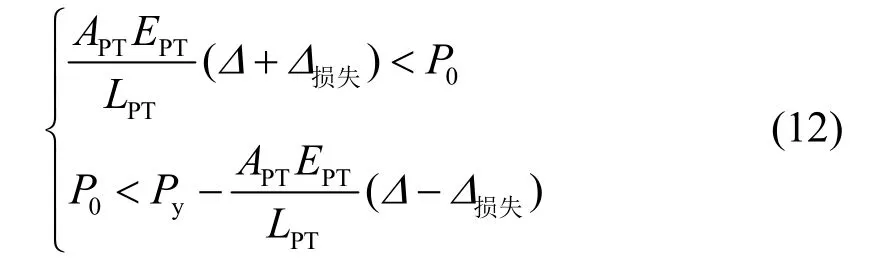
为简化计算,可忽略由于梁的轴向压缩导致的预应力损失,则公式(12)可简化为:

公式(13)可初选钢绞线初始预应力,通过有限元分析,调整和最终确定初始预应力值.
6 结论
提出了一种新型绕梁腹板销轴转动的自复位方钢管混凝土框架梁柱连接节点.推导了新型自复位方钢管混凝土框架的抗侧刚度计算公式,并通过有限元分析验证了公式的合理性,探明了自复位框架的失效机制,给出了钢绞线初始预应力取值建议.得到以下结论:
(1) 绕梁腹板销轴转动的自复位框架抗侧刚度与钢绞线材料属性、截面面积及其布置位置等有关,与框架梁、柱等构件截面无关.
(2) 新型自复位框架在循环荷载作用下,荷载-位移呈线性关系,荷载-位移曲线为过原点的直线,残余位移很小,具有良好的自复位能力.
(3) 由抗侧刚度公式和有限元参数分析可知,随着钢绞线截面面积增大,自复位框架侧向刚度和承载力增大;钢绞线处于弹性时,初始预应力大小对自复位框架侧向刚度影响很小.
(4) 对于单层自复位框架,当钢绞线截面面积较小时,理论值与有限元值吻合较好;对于多层自复位框架,当钢绞线截面面积较大时,理论值与有限元值吻合较好.抗侧刚度计算公式具有较好的适用性.
(5) 自复位框架存在两种失效机制,分别为一侧钢绞线应力减小为零或一侧钢绞线达到抗拉强度.合理选取初始预应力值可避免失效机制的发生.
References
[1] 中华人民共和国住房和城乡建设部和国家质量监督检验检疫总局联合发布. 建筑抗震设计规范: GB 50011-2010[S]. 北京:中国建筑工业出版社,2010.Ministry of Housing and Urban-Rural Development of the People's Republic of China and General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China Code for seismic design of buildings: GB 50011-2010 [S]. Beijing: China Architecture & Building Press, 2010.
[2] 张爱林, 张艳霞, 刘学春. 震后可恢复功能的预应力钢结构体系研究展望[J]. 北京工业大学学报,2013,39(4):507-515.ZHANG Ailin, ZHANG Yanxia, LIU Xuechun. Research outlook of earthquake resilient prestressed steel structures[J].Journal of Beijing University of Technology,2013, 39(4): 507-515.
[3] PRIESTLY M J N. Overview of PRESSS research program[J]. PCI Journal, 1991, 36(4): 50-57.
[4] RICLES J, SAUSE R, PENG S W, et al. Experimental evaluation of earthquake resistant posttensioned steel connections[J]. J. Struct. Eng., 2002, 128(7):850-859.
[5] MARIA M Garlock, JAMES M Ricles, RICHARD Sause.Experimental studies of full-scale posttensioned steel connections[J]. Journal of Structural Engineering, 2005,131(3):438-448.
[6] GARLOCK M, SAUSE R, Ricles J. Behavior and design of post-tensioned steel frame systems[J]. J. Struct. Eng.,2007, 133(3): 389-399.
[7] MIDORIKAWA M, ISHIHARA T, AZUHATA T, et al.Three dimensional shaking table tests on seismic response of reduced-scale steel rocking frames[C]// Proceedings of the 3rd International Conference on Advances in Experimental Structural Engineering. San Francisco,USA: Earthquake Engineering Research Center, 2009.
[8] 潘振华,潘鹏,叶列平,等. 自复位钢框架节点有限元模拟及参数分析[J]. 建筑结构学报,2011,32(3):35-42.PAN Zhenhua, PAN Peng, YE Lieping, et al. Modeling and parametric study of beam-to-column connection for self-centering steel moment frames[J]. Journal of Building Structures, 2011, 32(3): 35-42.
[9] 蒋成良,李启才. 钢绞线预应力的改变对自复位钢框架性能影响[J].苏州科技学院学报(工程技术版),2013,26(3):28-31.JIANG Chengliang, LI Qicai. Influence of prestress change in stand on seismic behavior of self-centering frame[J]. Journal of Suzhou University of Science and Technology(Engineering and Technology),2013,26(3):28-31.
[10] 张艳霞, 张爱林, 孙文龙. 震后可恢复功能的钢框架预应力梁柱节点性能研究[J]. 工业建筑,2014,44(11):160-167.ZHANG Yanxia, ZHANG Ailin, SUN Wenlong. Behavior study of self-centering beam-column connections in resilient steel frames after earthquake[J]. Industrial Construction, 2014, 44(11): 160-167.
[11] PATRICIA M. Clayton, DANIEL M. Dowden, TYLER Winkley, et al. Experimental investigation of self- centering steel plate shear walls[C]//Structures Congress,2012: 1586- 1597.
[12] 陈以一, 贺修樟, 柯珂, 等. 可更换损伤元结构的特征与关键技术[J]. 建筑结构学报,2016,37(2):1-10.CHEN Yiyi, HE Xiuzhang, KE Ke, et al. Characteristics and technical issues on structural systems with replaceable damage-concentrated elements[J]. Journal of Building Structures, 2016, 37(2): 1-10.
[13] PATRICIA M Clayton, TYLER B Winkley, JEFFREY W Berman, et al. Experimental investigation of self-centering steel plate shear walls[J]. Journal of structural engineering, 2012, 138:952-960.
[14] Dassault Systemes Simulia Corp. ABAQUS Analysis user's manual version 6.10[M]. Province, RI: Dassault Systemes Simulia Corp., 2010.

