低渗透储层非线性渗流压力传播规律

张琪琛， 陈民锋， 陈　璐， 吴　丽， 乔聪颖, 李晨辰

(中国石油大学 (北京) 石油工程学院，北京　102249)



低渗透储层非线性渗流压力传播规律

张琪琛， 陈民锋*， 陈璐， 吴丽， 乔聪颖, 李晨辰

(中国石油大学 (北京) 石油工程学院，北京102249)

摘要：低渗透油藏流体在地层中的流动一般表现出非达西渗流的特征，其在储层中的压力传播过程和压力分布规律与达西渗流明显不同.本文从分析开发中的不稳定渗流过程入手，建立了不同驱替压力梯度条件下的分段渗流数学模型，并采用稳定逐次逼近法，求解得到了拟线性渗流区与非线性渗流区的压力分布方程；基于实际油田开发情况，还系统地研究了在生产过程中非线性渗流条件下的压力传播规律，以及压力传播边界的压力分布规律，并对比分析了不同流动状态下的压力分布差别.研究表明：在生产过程中，随着压力波的向外传播，流体的流动由线性渗流转变为非线性渗流；而储层中的压力分布存在线性渗流分界点，且线性渗流分界点与井壁之间的距离随着压力波的传播先增大后减小，使得非线性流动区域不断增大.

关键词：低渗透油藏； 非线性渗流； 压力传播边界； 线性渗流分界点

0引言

低渗透储层由于启动压力梯度的存在及非线性渗流特征，其流体流动不再符合线性达西定律[1-3].目前，描述低渗透油藏渗流的模型主要为拟启动压力梯度模型、分段模型和连续模型三类[4].其中，拟启动压力梯度模型理论相对成熟，但该模型忽略了非线性渗流特征对储层流体的影响，对非线性渗流特征较强的低渗透油藏适用性较差；连续性模型主要分为三参数模型和两参数模型,三参数模型不能体现最小启动压力梯度对低渗透油藏的影响，而两参数模型无法反映非线性渗流特征的影响因素[5-10]；而分段模型则能够精确描述流体渗流过程中不同渗流阶段的渗流规律.

本文依据低渗透储层流体的非线性渗流特征，建立了非线性渗流分段数学模型，并提出逐次稳定迭代求解方法，分析研究了非线性渗流条件下的压力传播过程与分布特征.

1非线性渗流条件下压力传播过程及渗流方程基本解

1.1　压力传播过程分析

由于低渗透油藏存在启动压力梯度，故低渗透储层压力传播过程与常规油藏存在差异[11].根据低渗透储层非达西渗流特征曲线,如图1所示，其储层中流体流动状态随着驱替压力梯度的增大而变化，其中oa段为非流动段，ad段为非线性段，de段为拟线性段.定义a点为最小启动压力梯度、c点为拟启动压力梯度、b点为临界压力梯度[12].

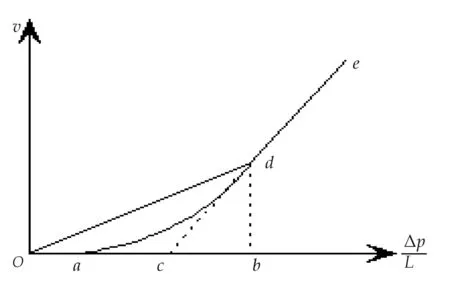
图1　低渗透非达西渗流特征曲线

非线性渗流条件下，渗流速度分段模型可表示为[12]：

(1)

式(1)中:c为拟启动压力梯度，MPa/m；a为最小启动压力梯度，MPa/m；b为临界压力梯度，MPa/m；k为储层渗透率，10-3μm2；μ为地层原油粘度，mPa·s；n为渗流指数，小数.

与常规基于启动压力梯度推导得到的压力分布相比，在分段模型条件下的压力分布分为两段表示，而且存在线性渗流分界点，与常规启动压力梯度模型压力传播过程有明显的差别.

采取分段模型描述储层中流体的渗流特征，其储层中相应的压力传播过程如图2所示.其中，定义两个新的相关物理参数:

①压力传播边界：在生产过程中，随着压力波的向外传播，在一定条件下压力波能够传播到的外边界.

②线性渗流分界点：在压力传播边界范围内，储层中线性渗流和非线性渗流的分界点.在开采过程中，线性渗流分界点以内的压力梯度较大，满足线性渗流条件，称为拟线性流动，而在线性渗流分界点以外的流动为非线性流动.

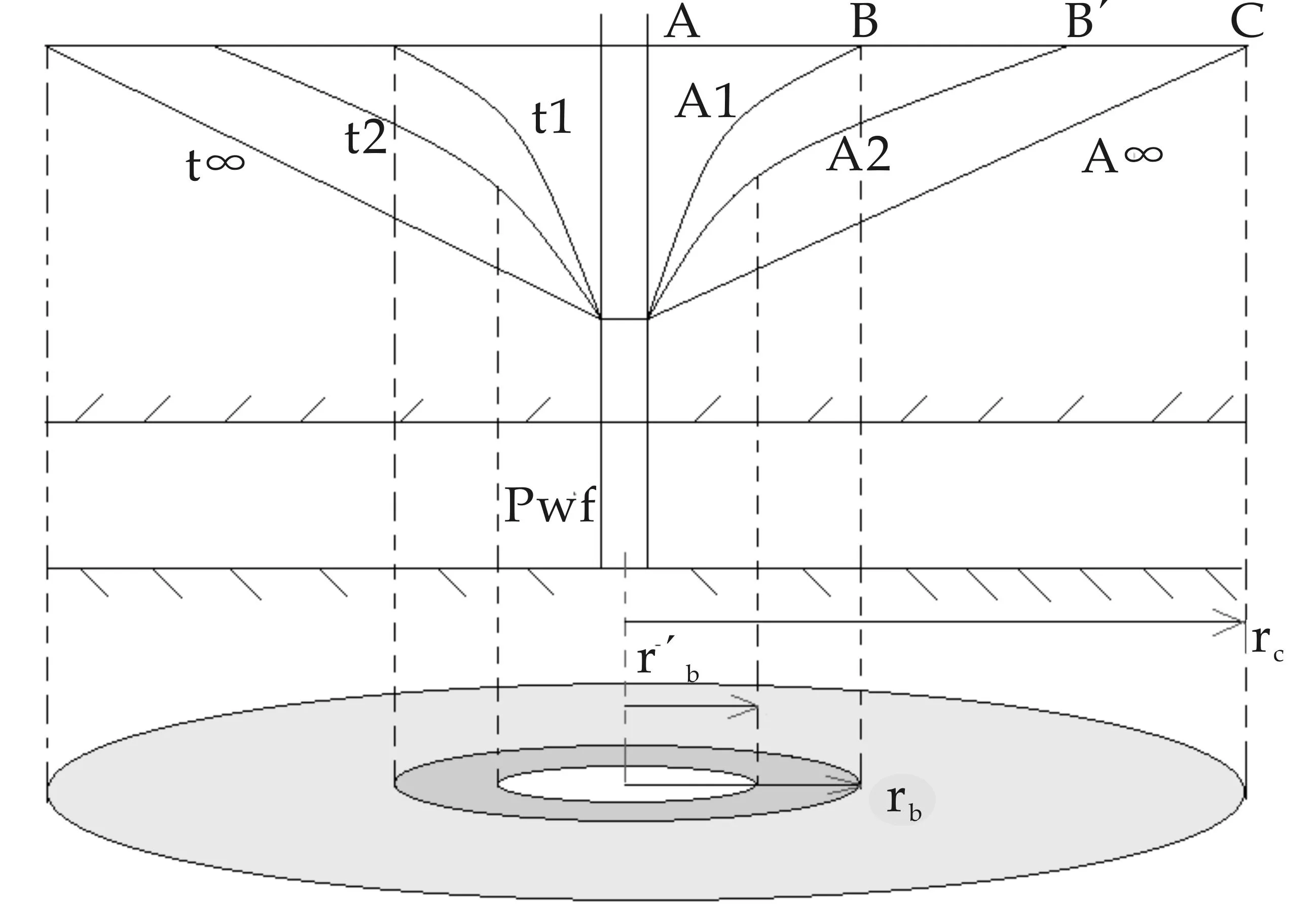
图2　储层中压力传播过程

当储层开始投入生产时，由于近井区域驱替压力梯度较大，储层中流体的渗流方式为拟线性流，随着压力波不断地向外扩张，储层中驱替压力梯度也不断下降.当压力波动边界传播至储层rb处时(图(2)中B处)，若此处驱替压力梯度恰好等于临界压力梯度，则半径rb以内储层流体渗流方式为拟线性流，而半径rb上的点即为线性渗流分界点;当压力波继续向外传播时，压力传播边界处的驱替压力梯度小于临界压力梯度，线性渗流分界点以外的储层流体渗流方式转化为非线性流.当压力传播边界到达B′时，此时的线性渗流分界点距井距离由rb变化为rb′.储层中存在半径rc(图(2)中C处)，此处驱替压力梯度小于等于最小启动压力梯度，使得该处渗流速度vc= 0，则半径rc即为极限动用半径.

1.2　非线性渗流方程的基本解

非线性渗流方程的求解采用逐次稳态逼近法，即将不稳定渗流过程中不同时刻的压力分布特征用稳态方法来描述，将压力传播的非稳态过程用一系列渐变的稳态过程来逼近[1].

非线性渗流方程为[13-15]：

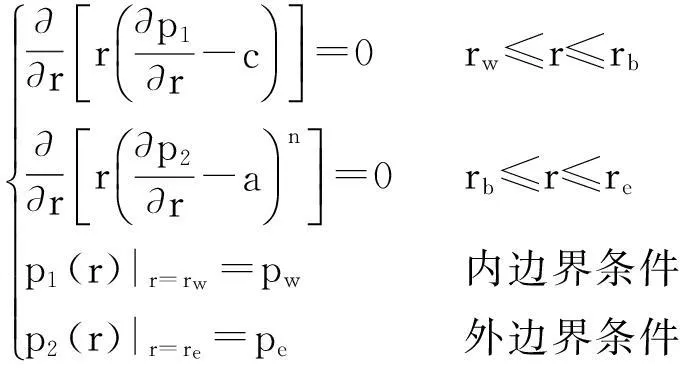
(2)

限制条件一，两种流动状态在线性渗流分界点处的压力相等：

p1(r)|r=rb=p2(r)|r=rb=prb

(3)

限制条件二，两种流动状态在线性渗流分界点处的渗流速度相等：

(4)

其中，rb为线性渗流分界点对应的距井距离;prb为线性渗流分界点处的压力.

通过求解方程组(2)，再利用限制条件(3)和(4)可以求得不同渗流阶段的压力分布表达式.

当rw≤r≤rb时，在线性渗流分界点以内，拟线性段压力分布表达式为：

c(r-rw)

(5)

当rb≤r≤re时，在线性渗流分界点以外，非线性段压力分布表达式为：

a(re-r)

(6)

公式(5)中的re′为拟线性渗流条件下的压力传播边界；式(6)中的re为储层流体在非线性渗流条件下的压力传播边界，re可以由re′求出，求解过程在章节1.3中.

将公式(5)、(6)对r求导，得到了不同渗流阶段的压力梯度表达式.

当rw≤r≤rb时，拟线性段压力梯度表达式为：

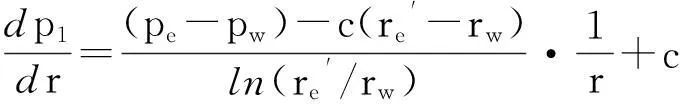
(7)

当rb≤r≤re时，非线性段压力梯度表达式为：

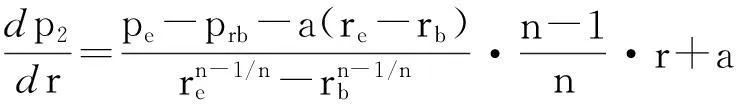
(8)

1.3线性渗流分界点及非线性压力传播边界的确定

由于储层中流体的渗流分为两个阶段，即拟线性渗流阶段和非线性渗流阶段，对应的储层渗流区域亦分为拟线性渗流区域和非线性渗流区域，而区分两个渗流区域的则是线性渗流分界点.

两个渗流区域的范围不是固定不变的，而是随着生产的进行而发生变化.因此,线性渗流分界点的确定，对于非线性渗流条件下压力传播边界的确定，以及渗流区域变化规律和流体渗流规律的研究具有十分重要的意义.

线性渗流分界点及非线性压力传播边界的求解步骤如下：

①在生产过程中，近井区域的压力梯度大于临界压力梯度，随着压力传播边界不断向外扩张时，压力传播边界处的驱替压力梯度值也不断减少.因此，根据公式(7)可以确定出线性渗流分界点的最大位置.

②根据拟启动压力梯度模型，令拟线性渗流条件下的压力传播边界为re′.利用不同位置re′，结合拟线性渗流压力梯度表达式(7)来确定不同的线性渗流分界点.

③根据限制条件(3)和(4)，并利用拟线性渗流条件下压力传播边界re′及其对应线性渗流分界点，应用迭代方法求解出非线性渗流条件下的压力传播边界re.

1.3.1线性渗流分界点的确定

在压力传播边界处的驱替压力梯度值减小到临界压力梯度之前，压力传播边界以内区域的储层流体渗流特征为拟线性的，因此,线性渗流分界点距井距离随压力传播边界的扩大而增加;当压力传播边界处驱替压力梯度值等于临界压力梯度时，此时线性渗流分界点距井距离达到最大值，即rbmax.根据公式(7)可得到：

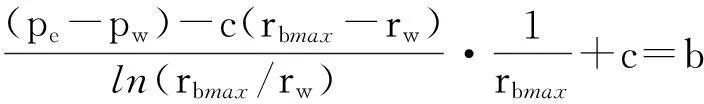
(9)

通过求解下文所述的隐式方程(11)可得到rbmax.

压力波到达线性渗流分界点距井最大距离位置后，压力波继续向外传播，当压力传播边界处的驱替压力梯度值小于临界压力梯度值时，压力传播边界内的储层流体会出现两种流动状态，即拟线性流和非线性流.由于压力波波及范围内储层各点的驱替压力梯度值随着压力传播边界的扩大而减少，因此,线性渗流分界点距井距离随着压力波向外传播而不断缩小.

假设当压力波到达线性渗流分界点距井最大距离rbmax后，压力波继续以拟线性渗流规律向外传播，根据公式(7)可以得到含有线性渗流分界点位置rb的隐式方程：

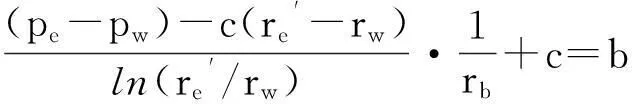
(10)

式(10)中:re′为拟线性渗流条件下压力传播边界，m.

迭代求解公式(10),可以得到拟线性渗流条件下，压力传播边界到达不同位置时对应的线性渗流分界点的不同位置rb.

1.3.2非线性压力传播边界的确定

由图1可以看出，拟启动压力梯度模型中渗流特征为图中ec段，若用线性渗流特征来代替曲线渗流特征对储层流体的影响，会人为地将最小启动压力梯度变大.因此，非线性渗流条件下压力传播边界re与拟线性渗流条件下压力传播边界re′是不同的，且re可以通过re′求出.根据限制条件(3)和(4)，可以求出储层流体在非线性渗流条件下压力传播边界re的隐式表达式：

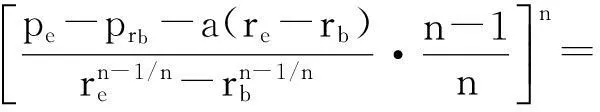
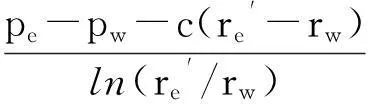
(11)

由公式(5)、(10)，可求出线性渗流分界点处的压力分布：

(12)

将公式(12)代入公式(11)，应用迭代方法求解隐式方程(11)即可求出非线性渗流条件下压力传播边界re.

根据拟线性渗流条件下压力传播边界re′，求解出线性渗流分界点和非线性条件下压力传播边界re，将求解出的rb与re代入公式(6)、(8)中，可以得到非线性渗流条件下的压力分布及压力梯度表达式,进而可以得到不同渗流阶段的分段压力分布表达式.

2开发过程中的压力分布规律

2.1　油藏参数取值

油藏基本参数如下：油藏原始地层压力为15.0 MPa；生产压差为5.0 MPa；储层渗透率 为30×10-3μm2；储层有效厚度为60 m；地层原油粘度为100 mPa·s; 最小启动压力梯度a为0.01 MPa/m；拟启动压力梯度c为0.03 MPa/m；临界压力梯度b为0.04 MPa/m.

由公式(4)、(7)、(8)可以求出渗流指数n：

(13)

将各参量代入到公式(13)中，求出渗流指数n=1.313 3.

2.2　开发过程中的压力传播规律

根据公式(5)、(6)可以得到分段模型的压力分布规律.为了能够更好地观察非线性渗流压力传播过程中非线性渗流区与拟线性渗流区的变化规律及压力分布特征，引入了具有相同线性渗流分界点的拟启动压力梯度模型.

基于示意图(如图2所示)，分段模型段压力传播边界到达不同位置A0、A1、A2、A3,…(不同开发阶段)时的压力分布规律分别如图3～6所示.

由图3~6可以看出:非线性渗流条件下的压力分布分为两段，在近井区域,压力波以拟线性渗流规律传播，在远井区域，压力波以非线性渗流规律传播；随着生产的进行，拟线性渗流区先增大后缩小，即线性渗流分界点距井壁的距离先增大后变小；储层中绝大部分区域为非线性渗流区域，只有近井的小部分区域为拟线性渗流区域;非线性渗流条件下压力波波及范围更大，在拟启动压力梯度模型中储层无法动用的地带,在非线性渗流模型中储层则是可以动用的.

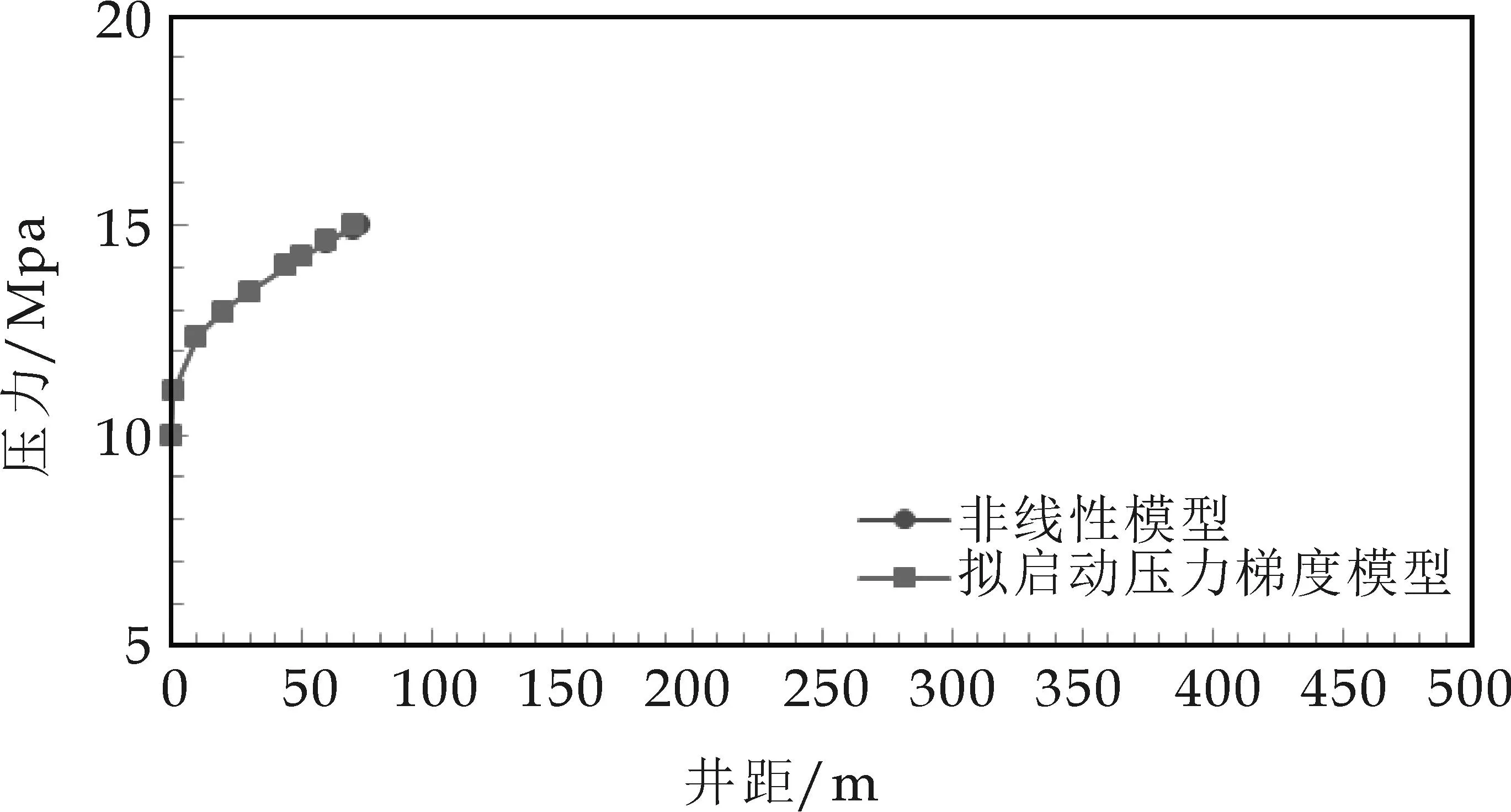
图3　A0位置非线性渗流压力分布规律

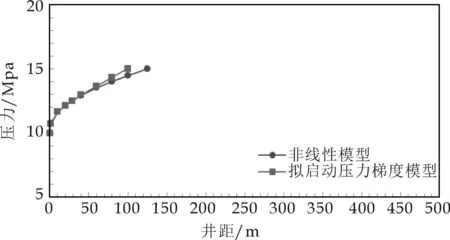
图4　A1位置非线性渗流压力分布规律

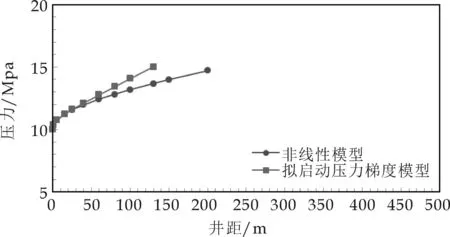
图5　A2位置非线性渗流压力分布规律

图6　A3位置非线性渗流压力分布规律

2.3　压力分布规律

基于上述分析，将不同位置的压力传播边界压力分布规律整合，得到了非线性渗流条件下压力波动边界传播到不同位置时的压力分布图,如图7所示.

图7　不同开发阶段非线性压力分布规律

由图7可以看出，随着生产的进行，地层的压力不断下降.压力波传播的距离越远，生产时间越长，地层中压力分布呈线性分布的范围就越大.当压力波动边界传播到极限半径处时，储层中绝大部分区域处于非线性渗流区，只有近井极小范围内处于拟线性渗流区.

不同渗流模型下，其压力传播边界传播到同一位置时的压力分布规律如图8所示.

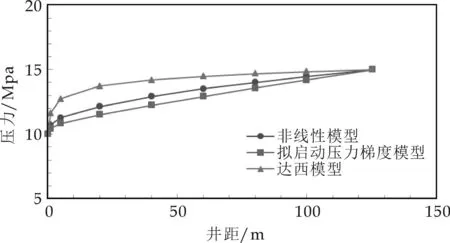
图8　不同模型压力分布曲线图

由图8可以看出，三类流动状态下，压力分布规律大体一致，压力均是以漏斗形式分布于储层之中.其中，同样的规律是：近井地带压力梯度大，压力损耗大，占整个生产压差的比例高，而远井地带曲线变得较为平缓.

不同的规律是：在压力波传播过程中，达西渗流所需要的压力梯度最小，消耗储层压力最小；拟线性渗流所需压力梯度最大，消耗储层压力最大；非线性渗流介于两者之间.因此,对于非线性渗流特征明显的低渗透油藏，忽略非线性因素对储层流体渗流的影响，会造成较大的误差.

一般在实际油田开发工程计算中，储量极限动用半径等于储层中渗流速度为零处所对应的泄油半径[1].根据上述方法并结合油藏实际开发数据，如图6所示，得到拟启动压力梯度模型的极限动用半径为166.77 m，而非线性分段模型得到的极限动用半径为500.10 m；在开发初期，渗流速度较大，随着压力波的向外传播，储层中流体渗流速度越来越小，逐渐转变为低速的非线性流动，在这种状态下，相比于拟启动压力梯度模型计算结果，压力波传播的范围有很大地增加.因此，对于低渗透油田开发，流体渗流的非线性特征对储层极限动用影响很大，非线性分段模型能够更加精确地描述低渗透储层流体渗流规律.

3结论

通过上述研究，可以得出以下结论：

(1)低渗透储层在生产过程中，其储层中渗流存在拟线性渗流区和非线性渗流区，两渗流区之间存在线性渗流分界点.随着生产的进行，线性渗流分界点距井壁的距离先增大后减小，而储层中非线性渗流区的范围则不断增大，且储层中绝大区域属于非线性渗流区.

(2)在非线性特征较强的低渗透储层中，非线性渗流段对压力分布规律的影响不可忽略，应用分段模型能够精确描述低渗透储层在非线性渗透条件下的压力分布规律.

(3)与拟启动压力梯度模型相比，分段模型可以更准确地描述低渗透储层中的渗流规律;基于分段模型计算的压力波及范围相对较大，对合理开发井距的确定更为准确.

参考文献

[1] 陈民锋，李晓风，赵梦盼，等.启动压力影响下确定油藏有效动用半径[J].断块油气田，2013，20(4):462-465.

[2] 黄延章．低渗透油层渗流机理[M]．北京：石油工业出版社，1998．

[3] 吕成远，王建，孙志刚．低渗透砂岩油藏渗流启动压力梯度实验研究[J]．石油勘探与开发，2002,29(2):86-89．

[4] 杨仁锋，姜瑞忠，刘世华，等.特低渗透油藏非线性渗流数值模拟[J].石油学报,2011,32(2):299-306.

[5] 时宇,杨正明,黄延章.低渗透储层非线性渗流模型研究[J].石油学报, 2009，30(5):731-734.

[6] 杨正明,于荣泽,苏致新,等.特低渗透油藏非线性渗流数值模拟[J].石油勘探与开发，2010， 37(1):94-98.

[7] 窦宏恩，杨旸.低渗透油藏流体渗流再认识[J].石油勘探与开发，2012， 39(5):633-640.

[8] 邓英尔,刘慈群.低渗透油藏非线性渗流规律数学模型及其应用[J].石油学报,2001,22(4):72-77.

[9] 姜瑞忠，杨仁锋，马勇新，等.低渗透油藏非线性渗流理论及数值模拟方法[J].水动力学研究与进展,2011,26(4):444-452.

[10] 杨清立，杨正明，王一飞，等.特低渗透油藏渗流理论研究[J].钻采工艺，2007,30(6):52-54.

[11] 计秉玉，何应付．基于低速非达西渗流的单井压力分布特征[J].石油学报，2011,32(3)：466-469．

[12] 时佃海.低渗透砂岩油藏平面径向渗流流态分布[J].石油勘探与开发,2006,33(4):491-494.

[13] 黄延章.低渗透有层非线性渗流特征[J].特种油气藏,1997,4(1):9-14.

[14] 孙玉凯，宋洪庆，朱维耀，等．低渗透油藏非达西渗流地层压力计算方法及分析[J]．岩土力学，2009，30(2):138-141．

[15] 罗成栋，章彤，钟飞翔，等.一种求解低速非达西渗流试井模型的新方法[J].断块油气田，2004，11(3)：79-82．

【责任编辑：晏如松】

Transmission of pressure in low permeability

reservoir with non-linear seepage

ZHANG Qi-chen, CHEN Min-feng*, CHEN Lu, WU Li,

QIAO Cong-ying, LI Chen-chen

(College of Petroleum Engineering, China University of Petroleum(Beijing), Beijing 102249, China)

Abstract:Fluid flow in low permeability reservoir conforms to non-Darcy seepage，the distribution and transmission of pressure are obviously different in Darcy and non-Darcy seepage.This paper starts with the analysis of the process of unstable seepage in the oilfield development,and set up a multi-stage mathematic model,which in different pressure gradient is taken into accounted.A method of steady-state successive approach to unsteady-state solution is used to get the equation of the distribution of pressure in quasi-linear and non-linear seepage region in different condition of displacement pressure gradient.Based on oilfield cases, the transmission and distribution of pressure in the condition of non-linear seepage are studied systematically,besides,the difference of distribution of pressure in different flow state is analyzed.The analysis shows that,in the process of production,the flow of fluid is changed from the linear Darcy flow to the non-linear seepage flow;In the condition of non-linear seepage,there is a linear seepage demarcation point,and the distance between borehole wall and linear seepage demarcation point increases to the maximum and then starts to decrease,while the non-linear seepage region increases with the transmission of pressure.

Key words:low permeability reservoirs; non-linear seepage; pressure transmission boundary; linear seepage demarcation point

中图分类号：TE348

文献标志码：A

文章编号：1000-5811(2016)01-0102-05

通讯作者:陈民锋(1971-)，男，河南清丰人，副教授，博士，研究方向：油田开发系统理论方法、三次采油技术,cmfllp96@126.com

作者简介:张琪琛(1990-)，男，黑龙江鹤岗人，在读硕士研究生，研究方向：油田开发系统理论方法

基金项目：国家973重点基础研究计划项目(2015CB250905)