低渗透矩形油藏不稳定渗流压力动态分析
刘海龙


摘要:目前,低渗透矩形油藏地层渗流压力求解的研究比较成熟,但是对于渗流压力的动态分析及渗流压力影响因素分析的研究尚存在一些不足。针对低渗透矩形油藏难动用的难题,基于两参数连续模型,运用稳态逐次替换法,分别建立了定压和定产两种生产形式下的压力动态分析模型,并从地层物性和导压系数两个层面进行了相关因素分析。分析认为:无论在定产模型还是在定压模型中,压力传播距离与时间均为二次三项式关系,且压力传播快慢与产量、渗透率呈正相关,与流体黏度、井底流压、启动压力梯度呈负相关。实例计算表明:所建立的模型可靠,为矩形油藏注水开发,预计注水见效时间,提供一定的理论依据。
关键词:矩形油藏;低渗透油藏;不稳定渗流
中图分类号:TE1211 文献标志码:A文章编号:1672-1098(2016)01-0075-08
Abstract:At present, the research on solution of seepage pressure in low permeability rectangular reservoir formation is relatively mature. However, there are still some deficiencies in the study of dynamic analysis of the seepage pressure and the influencing factors on seepage pressure. Aiming at the difficult problem of low permeability rectangular reservoir, based on the two-parameter continuous model, the dynamic analysis models for constant pressure or fixed production were established separately by using the steady state successive substitution method, and the related factors analysis was carried out from the aspects of the formation characteristics and the pressure coefficient.The analysis showed that whether in the fixed production model or in the constant pressure model, the relationship between the pressure propagation distance and time is quadratic trinomial, and the speed of pressure propagation is positively correlated with the yield and the permeability, but negatively correlated with the viscosity of the fluid, the bottom hole flowing pressure and the starting pressure gradient.Example calculation showed that the models are reliable, which can provide some theoretical basis for the rectangular reservoir development by water injection and for the calculation of expected effective time of water injection.
Key words:rectangular reservoirs; low permeability reservoirs; unsteady seepage
随着我国国民经济稳定增长,石油需求不断增加,我国已经成为仅次于美国的世界第二大石油消费国[1]。但是由于中、高渗透油藏后备石油储量不足,每年新增探明储量中,低渗透油藏比例越来越大,因此加速开发低渗透油藏,意义重大[2]。
目前,我国的老油田开采面临两大难问题:高含水和低渗透。针对于低渗透的研究,前人已经做出了很多研究,且取得了重大进展:如马尔哈辛提出低渗透油藏存在启动压力梯度,并从微观角度解释了其产生的机理[3];Pascal 等人首次应用数值积分方法——有限差分法[4-5],在考虑启动压力梯度条件下,求解流体渗流压力分布。
宋付权等人结合室内实验,建立低渗透油藏岩心一开一关渗流数学模型,对一维压力传播边界进行数值求解[6];李凡华等人考虑启动压力梯度,建立了无限大和有界低渗透油藏不稳定渗流试井分析模型[7];邓英尔等人在实验的基础上,首次提出非达西渗流连续函数模型,并建立了非线性稳态渗流的压力和产量公式[8];刘鹏程等人结合室内实验和油田实际生产,提出压敏分段变化理论,并在此基础上给出了油气井单井产能公式和产量预测方法[9-10];郝明强等人考虑启动压力梯度和压敏效应,通过拟压力变换,推导了平面径向流压力分布公式[11]。朱圣举采用稳态逐次替换法,给出了不同渗流方式下,低渗透油藏孔隙中弹性流体低速不稳定渗流压力的传播规律[12]。杨清立提出的两参数非线性连续模型既反映出流体在低渗介质中渗流时存在最小启动压力梯度的现象, 又可以很好地描述非线性段特征[13]。姜瑞忠基于两参数模型,采用数值模拟方法,建立了两维两相非线性渗流数值模型[14]。但是目前针对于压力传播规律的研究还很欠缺,且大多只考虑拟启动压力梯度,认为低渗透油藏渗流的启动压力梯度与油藏本身的无关,其无法真实反映地下流体的渗流特征。或是基于一维径向渗流[15],或是研究定产量生产[16],然而实际生产中,存在定井底流压生产情况,且对于生产中的大型线性排状注水,或是渗流物理模拟实验,流体会发生一维单向流动,因而有必要对低渗透油藏不稳定渗流压力进行动态分析。
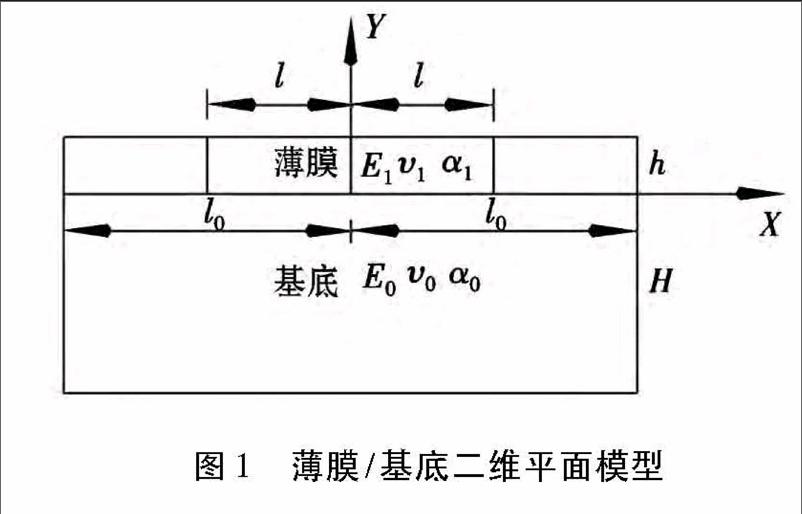
1物理模型
为一平面带状等厚低渗油藏,地层流体微可压缩,粘度为μ,油藏平均厚度为h,宽度为w,长度为L,地层外边界压力为pe,井底流压为pwf,油藏中一口井以定产量或是定井底流压方法生产,储层中的流体以不稳定渗流形式流向井筒。
目前非线性渗流的数学模型描述方法很多[17-19],如表1所示。
dpdx=-(a-1-bN)+(a-1-bN)2+4abN2b=
-(a-1-bN)+(a-1+bN)2+4bN2b(4)
对(4)式进行讨论,当a→∞,b→0时,(4)式可简化为dpdx=N=μqwkh,此解与达西定律对应,验证了解析解是正确的。
利用文献12中的稳态逐次替换法,可得
由式(12)可知,压力传播与时间成幂指数关系,这与中高渗油藏的一维压力传播与时间为线性关系不同。原因在于低渗透油藏本身孔喉小,在压力敏感效应下,孔喉直径缩短为原始的70%[21]。且存在启动压力梯度,尤其是储层能力不足时(压力系数太小,小于1时),使得孔隙流体压力不足以传播到井筒,启动压力梯度影响更为明显。低渗透油藏在两种机制作用下,压力传播速度变慢,传播规律发生变化。
对于实际油田开发而言,要提高压力传播速度,必须借助外来能量来补充地层能量的不足,如注水或注气,从而提高储层孔隙流体压力,减小或消除启动压力梯度的影响,进而使得油田正常开发。采用压裂改造低渗透储层,在储层中建立“流动网络”,联通储层更多的渗流通道,增大储层暴露的渗流面积,加上外部注水或注气,提前补充地层能量,增加储层压力,减小储层流体渗流阻力,使得低渗透储层启动压力梯度减小或“消失”。
1) 模型应用。取文献16的参数:低渗透油藏地层原始压力为30 MPa,孔隙度为012,渗透率为12 mD,流体黏度为0256 mPa.s,启动压力梯度为002 MPa/m,流量为10 m3/d,矩形油藏长、宽、高分别为100 m、20 m、5 m,a、b取值为0908、105。将上述数据代入式(12),并与表1中的拟压力梯度模型和达西模型作对比,结果如图2所示。
t/d
1. 拟启动压力梯度模型;2. 拟线性模型;3. 达西模型
图2显示了不同渗流模型下压力传播的范围和深度,三种模型的趋势大致相同,在井筒附近压降梯度最快,远离井筒处的压降梯度慢慢变缓。当压力传播距离相同时,非线性模型所用时间比拟启动压力梯度模型的小,比达西模型的大,这是因为在低渗透油藏中,当压力达到最小启动压力梯度时,地层中的流体就开始流动,而启动压力梯度模型中,只有当压力克服拟启动压力梯度时,流体才可以流动,故在传播相同距离时,所用时间要长。相反,由于达西模型不考虑启动压力梯度的影响,因而在传播相同距离时,用的时间最少。各模型计算结果相差很大,低渗透、特低渗透油藏由于具有明显的非线性渗流特征,采用线性模型分析问题,必然会导致较大的误差,因此建议使用非线性模型进行相关问题的分析和计算。
随着油田实际生产的进行,压力传播的动边界逐渐往外扩大,分别取x=20 m,40 m,60 m,80 m,100 m,将数据带入式(12),观察其压力随时间的变化规律,如图(3)所示。再取t=60 d,70 d,80 d,90 d,观察各时间地层中的压力分布规律,如图(4)所示。
由图3知:随着油井的采油,压力逐渐向边界扩展,当动边界扩展到20 m,40 m,60 m,80 m,100 m时,压力降落漏斗急剧增大,尤其在井筒附近表现最为突出,地层压力不断降低。图4显示:不同时间,压力波及的范围不一样,地下压力存在压力波及区和未波及区,井筒附近的压力变化最为明显,越偏离井筒,压力降落速度偏低。
2) 单因素分析。压力传播快慢受控于地层物性、温压力系统等因素,考虑实际生产需要,本文主要研究产量、渗透率、黏度等对压力传播快慢的影响。分别取图5表明:随着渗透率的增大,压力传播的越来越快(动边界往外扩散速度增大),因为渗透率增大,地层流体流动能力增强,相应的地层阻力减小,压力波更容易向外传播,进而动边界向往移动速度增大。
图6显示:随着黏度的增大,压力传播的越来越慢(动边界往外扩散速度减小),这是因为地层流体黏度越大,流动阻力就越大,需要更多的时间克服阻力流动,压力传播速度变慢,动边界往外扩散速度降低。
由图7知,对于同一时间,随着采油量的增加,压力传播的越远,即压力传播的越快。因为在相同时间内,增加采油量,就必须提高地层流体的流速,则就需要提高压力梯度,但是对于定边界压力的低渗透油藏,相同距离的压力梯度是一样的,为达到压力梯度在时间上的不一致,就必须使压力传播的更快,才能满足油井产油量增加。反过来,采油量的增大,生产压差也会在一定程度上增加(以增大生产压差提高油井产量),需要压力扩散到更大的空间范围,增加压力激动区的面积,即表现出,压力传播相同时间时,随着油井产量的提高,压力传播的越快、越远。
式(17)定压条件下,时间与压力传播距离关系式。与定产模型呈现类似的规律。式(17)表明:定井底流压条件下,矩形油藏压力开始降落,呈“漏斗状”向外扩展,只是压力在近井壁处近似为一定值,当压力传播到边界时,由于边界压力一定,这时为保持这种定井底流压的情况,必须对地层补充能量,此时油井的产量主要是两部分:一部分是边界进入地层的流体,q1,并且流量逐渐增加;另一部分是边界内部地层依靠弹性能量膨胀产生的流体q2,但是却逐渐减少。当油井产量为q1时,由不稳态渗流转变为稳态渗流。
1) 模型应用。由式(17)知:时间与压力传播距离为二次三项式,若井底流压为75 MPa时,数据相关数据代入式(28),并依此取启动压力梯度为002 MPa/m,007 MPa/m,020 MPa/m和渗透率为025 mD,050 mD,10 mD,20 mD得到定压生产10 d的压力传播规律,如图8所示。
由图8知:启动压力梯度和渗透率均能在一定程度上减缓压力传播速度。启动压力梯度大,地层阻力大;渗透率大,地层阻力小。两种因素相互制约,由于启动压力梯度是低渗透油藏储层本身的属性,通过外部很难改变,但是地层渗透率却是可以改造的。目前工艺上主要采用压裂、酸化进行,低渗透油藏更多采用压裂进行增产。
2) 单因素分析。同理,如212所述,本文主要研究井底流压、渗透率等对压力传播快慢的影响。分别取pwf=12 MPa,14 MPa,16 MPa,18 MPa观察压力
由图9知:图形斜率逐渐变小,压力传播速度减小,直到压力波及到边界。主要是因为传播距离越远,耗散的能量越大,若得不到外界能量的及时补给,则地层流体无法克服地层阻力,从而使得油井产量下降,这也是诸多低渗透油藏采用注水开发,补给地层能量的原因。当传播距离不大时,井底流压的影响较小,随着距离的增大,井底流压的影响增大。
减小井底流压,放大生产压差,可以有效提高油井产量,但是并非井底流压越小越好,而是油井以最合理的井底流压生产,可实现油井高效、稳定开发。(14)式解出x(t),并代入(17)式,求解得合理井底压力为
pwf=pe-(a2-a)2b[(bfa-1)+
(bfa-1)2+8b2a2μBfkφ0ct(1-a)](22)
f=(1-a)2[a+ab-(b-1)a2] (23)
将文献17数据代入式(22)得合理井底压力为1031 MPa,对应的最大产油量326 m3/d。
3实例分析
我国部分地区由于长期受到地质活动的影响,导致这些地区出现了很多的复杂断块油藏,苏北的台兴油田是一个典型的狭长型低渗透复杂断块油田[22-23]。该油田由于受到多级断层相互作用,使得台兴油田发育Ⅲ-Ⅴ级断层11条,断层将整个台兴油田分为11个含油断块。每个含油断块都有独立的温度、压力系统,每个小油藏形状近似矩形,宽度较小,长度较长,符合本文模型的应用条件。下面以文献23中的区块为例,进行实例分析。
目前数值模型的理论是建立在经典达西渗流基础上的,而Eclipse2010中的E300模块是针对低渗透油藏,考虑了启动压力梯度,因此将本文的定产模型计算的某时刻的井底流压(定产解)与数值模拟结果(数值解)对比,如表2所示。由表2可知,相对误差基本控制在8%内,说明定流压模型是可靠的。
表2定产模型实例计算对比表
时间
/d定产解
/(m3·d-1)数值解
/(m3·d-1)相对误差
/% 1017492161717552 2017202158837668 3016951156317787 4016729154127873 5016532152157966 6016355150438022 7016194148848089 8016048147388163 9015913146098195
由于定流压模型中,设定井底流压为常数,因此将式(17)带入式(14),求得不同时刻的产量(定压解),并与数值模拟(数值解)对比,如表3所示。由表3可知,相对误差控制在77%内,则定流压模型是可靠的。
表3定流压模型实例计算对比表
时间
/d定压解
/(m3·d-1)数值解
/(m3·d-1)相对误差
/% 10271225097485 20285527134974 30327930726313 40313933807678 50365938966477 60423845216678 70560159295856 80691772464756 4结论
1) 定产模型中,时间与压力传播距离为二次三项式关系,且在压力传播速度上,两参数连续模型比达西模型慢,比拟启动压力梯度模型要快,与流体黏度呈负相关,与产量、渗透率呈正相关;
2) 定压模型中,时间与压力传播距离亦为二次三项式关系,但压力传播速度与渗透率呈正相关,与井底流压、启动压力梯度呈负相关。
3) 实例计算表面,建立的定产模型、定压模型是可靠的。
参考文献:
[1]胡文瑞.中国低渗透油气的现状与未来[J].中国工程科学,2009,11(8):29-37.
[2]王光付,廖荣凤,李江龙,等.中国石化低渗透油藏开发状况及前景[J].油气地质与采收率,2007,14(3):84-89.
[3]MILLER R J.Threshold gradient for water flow in clay system, Proc[J].Soil.Sci.Soc.Am.,1963,27:606-609.
[4]PASCAL.F.Consolidation with Threshold Gradient[J].Inter.J. for Numerical and Analytical Methods in Geomechanics.1980,5:247-261.
[5]ALVARO,P,FARUK C.Mddification of Darcys law for the threshold pressure gradient,[J].Petrol.Sci.Eng.1999,22(4):237-240.
[6]宋付权,刘慈群,李凡华.低渗透介质含启动压力梯度一维瞬时压力分析[J].应用数学和力学,1999,20(1):25-33.
[7]李凡华,刘慈群.含启动压力梯度的不定常渗流的压力动态分析[J].油气井测试,1997,6(1):1-4.
[8]邓英尔,刘慈群.低渗油藏非线性渗流规律数学模型及其应用[J].石油学报,2001,22(4):72-77.
[9]刘鹏程,王晓冬,李素珍,等.地层压敏对低渗透气井产能影响研究 [J].西南石油学院学报,2004,26(5):37-41.
[10]刘鹏程,王晓冬,万玉金.三区复合油藏有限导流垂直裂缝井井底压力动态分析[J].油气井测试,2004,13(1):4-7.
[11]郝明强,胡永乐,李凡华.微裂缝性特低渗透油藏产能研究[J].石油天然气学报,2009,31(2):100-104.
[12]朱圣举.低渗透油藏的压力波传播规律[J].新疆石油地质,2007, 8(1):85-87.
[13]杨清立,杨正明,王一飞,等.特低渗透油藏渗流理论研究[J].钻采工艺,2007,30(6):52-54.
[14]XU J.Non-Darcy flow numerical simulation for low permeability reservoirs,SPE 154890.
[15]史瑞娜,王晓冬.低渗透地层压力扰动传播规律[J].特种油气藏,2011, 18(4):80-82.
[16]黄爽英,陈祖华.引入启动压力梯度计算低渗透砂岩油藏注水见效时间[J],河南石油,2011,15(5):22-24.
[17]BAOQUAN ZENG,LINSONG CHENG,CHUNLAN LI.Low velocity non-linear flow in low permeability reservoir[J].Petrol.Sci.Eng.2011,80(1):1-6.
[18]李松泉,程林松,李秀生,等.特低渗透油藏非线性渗流模型[J].石油勘探与开发,2008,35(5):606-612.
[19]XU J.Transient pressure behavior for dual porosity low peameability reservoir based on modified darcy.s equation[C]//SPE 153480.

