蒙特卡洛仿真在出版社生产计划决策上的应用

游少波

目前出版社的退货率不低，在生产计划阶段的决策失误，是造成库存的主要原因之一。因此，我们用蒙特卡洛仿真模型来对出版社的生产计划作前期模拟是极具意义的。

热词：蒙特卡洛仿真 生产计划 应用

出版社的生产计划包括以下几部分：一是确定图书新产品的定价;二是首次印刷的数量;三是确定在营销上的投入规模;四是赢利的情况预测。

出版社在制定生产计划时会遇到一系列问题，如产品的定价问题、营销费用的投入比例问题以及由此带来的成本与利润的关联问题等等。如果有若干同类产品竞争，消费者首先看重的就是产品价格。作为供应链上游的出版社，以最低的成本赚取最大的利润就是最终目标。而增加利润的最简单的办法就是在保证图书内容质量的前提下，尽可能地将书价定得高一些。但在目前的市场环境下，这样做的风险很大，如果书价定得不合理，不但终端读者不接受，处于供应链中间环节的批发商和零售商也会考虑到市场的接受能力，从而对产品进货数量产生疑虑。图书上市后，出版社有时会在营销方面投入宣传费用，但营销费用投入多少是合理的呢？这种投入与产品定价和印数的关系如何？赢利的预测情况会怎样呢？会不会产生库存积压？这些问题对于出版社是非常关键的，如果解决不好，必将使产品销售的前景变得不明朗。

由于图书产品的需求是随机事件，因此，我们用蒙特卡洛仿真模型来对出版社的生产计划作前期模拟是极具意义的。

传统的风险估计方法通常是估算出若干种不同情况下的系统性能，例如最好情况下的利润与最坏情况下的利润，然后进行分析。这种方法称为“what-if”分析法。但这种分析一般难以全面地、综合地、详细地描述风险的大小。蒙特卡洛方法是研究随机事件规律的一种仿真技术。蒙特卡洛方法的基本原理是：运用一连串随机数来表示一项随机事件的概率分布;然后利用任意取得的随机数从该项概率分布中获得随机变量值。

由概率定义知，某事件的概率可以用大量试验中该事件发生的频率来估算，当样本容量足够大时，可以认为该事件的发生频率即为其概率。因此，可以先对影响其可靠度的随机变量进行大量的随机抽样，然后把这些抽样值一组一组地代入功能函数式，确定结构是否失效，最后从中求得结构的失效概率。蒙特卡洛仿真方法正是基于此思路进行分析的。

蒙特卡洛仿真的逻辑流程是：设有统计独立的随机变量Xi（i=1，2，3，…，k），其对应的概率密度函数分别为fx1，fx2，…，fxk，功能函数式为Z=g（x1，x2，…，xk）。

首先根据各随机变量的相应分布，产生N组随机数x1，x2，…，xk值，计算功能函数值Zi=g（x1，x2，…，xk）（i=1，2，…，N），若其中有L组随机数对应的功能函数值Zi≤0，则当N→∞时，根据伯努利大数定理及正态随机变量的特性有：结构失效概率，可靠指标。

从蒙特卡洛方法的思路可看出，该方法回避了结构可靠度分析中的数学困难，不管状态函数是否非线性、随机变量是否非正态，只要模拟的次数足够多，就可得到一个比较精确的失效概率和可靠度指标。

现在我们可以用蒙特卡洛仿真来对出版社的生产计划进行仿真。出版社计划出版一本新书并制定了几个生产方案，已知单位定价可以采取18元、20元和25元三种方案，但不同的产品定价会带来市场不同的需求量。在三种方案里，营销费用可以变化，如果定价越高，读者接受能力越低，需要投入的宣传费用也将更大。不同的定价也会造成需求量的正态分布和标准方差的不同。现在，需要对几种不同的方案做出比较并决定采取何种方案。已知固定成本是100000元。我们可以运用蒙特卡洛仿真法对这三种方案连续做500次仿真，以求得最佳的方案。

已知条件：

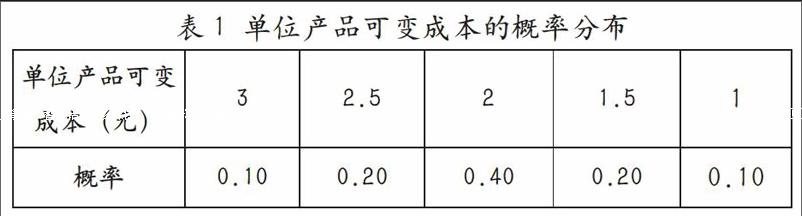
此表的数据表示单位产品的可变成本的概率分布。因为目前的图书产品的主要可变成本包括纸张价格的变化、水电成本、选择新技术产生的成本等。这些数据来源于出版社的出版科，根据历次印刷中的可变因素发生的概率得出。

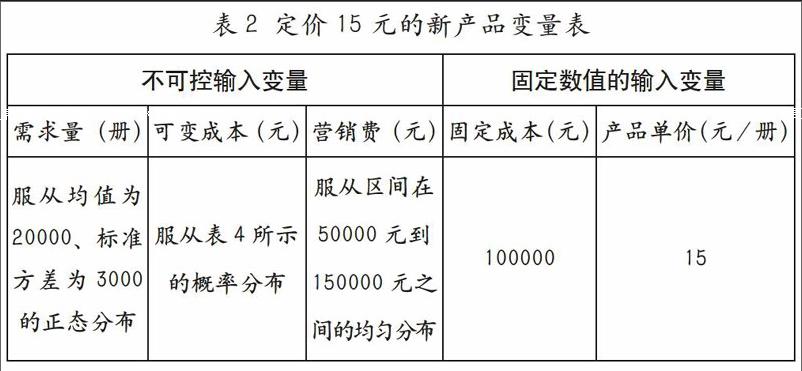
该新产品的投产有3个不可控的输入变量：需求量、可变成本和营销费;有2个固定数值的输入变量：产品的固定成本、产品价格。以产品定价15元为例，数据如表2。

如果我们用传统的风险分析方法计算：

最大利润=（单价-最低可变成本）×平均需求量-最低营销费用-固定成本=（15-1）×20000-50000-100000=130000（元）

最小利润=（单价-最高可变成本）×平均需求量-最高营销费用-固定成本=（15-3）×20000-150000-150000=-60000（元）

由此可得，新产品的最高利润为130000元，最低利润为-60000元，即亏损60000元。

传统的风险分析方法忽略了随机因素，仅考虑若干情况下的结果，如最好结果和最差结果。蒙特卡洛方法则是运用一连串随机数来表示一项随机事件的概率分布;然后利用任意取得的随机数从该项概率分布中获得随机变量值。

在本案例中，有3个不可控的随机输入变量：需求量、可变成本和营销费。其中需求量可以从同类产品的销售中得出服从均值为20000、标准方差为3000的正态分布，由此取均值20000作为产品的需求量;可变成本是在1元至3元之间、服从表1所列的概率分布的随机数;新产品所需的营销费是在100000元至150000元之间。另外，该产品的固定成本为100000元，产品单价为15元。

我们现在运用仿真模型对该新产品的风险进行分析。首先生成一系列随机数以代表不可控变量的概率分布，得到不可控变量的抽样值，然后输入到反映系统运行规律的相应的公式（模型）中进行仿真，最后对仿真结果进行统计分析。在Excel可以采取四个步骤来进行运算和统计。

第一步，输入已知数据

即在单元格中分别输入产品的单价和固定成本、需求量（正态分布）的均值和标准方差、营销费（均匀分布）的最小值和最大值、可变成本以及根据其概率分布得到的对应的随机数区间、可变成本的各个可能值、各可变成本对应的随机数区间的下限与上限。

随机数之间的下限与上限是根据可变成本的概率和累计概率确定的。我们可以根据以往出版行业可变成本发生的概率，得出其对应的随机数区间如表3。

第二步，生成一系列随机数，得到不可控输入变量的抽样值

本案例中不可控输入变量是：需求量、营销费和可变成本。在Excel上产生一系列随机数，可以得到不可控变量的抽样值。

选取单元分别表示需求量、营销费和可变成本的一组抽样值。在单元格中输入公式，可得到按正态分布的需求量抽样值，将上述公式复制499个单元格，得到另外499个需求量抽样值。

第三步，仿真运算

用某个单元格表示利润，用下述公式计算利润：

利润=（单价-可变成本）×需求量-营销费用-固定成本

同样将上述公式复制到499个单元格，得到另外499个抽样值下对应的利润。

第四步，统计分析

为了使得结果更加符合实际情况，通常需要进行多次仿真。本案例中已经进行了500次仿真，即对500格抽样值进行了仿真运算，得到了500个运算结果（利润），最后对这些运算结果进行统计分析。统计结果中可利用公式计算产品的平均利润值、标准方差、最大利润和最小利润、亏损的次数与概率，还可以根据需要计算其他统计量。例如，可用count if命令计算利润超过10万元的概率，等等。

我们可以将仿真结果展示如下：

从产品风险仿真的统计结果可以看出，该新产品的平均利润约为59939元，标准方差约为49593元，最小利润约为-94842元，最大利润约为224923元，亏损的概率是10%。

此外，我们还可以根据新产品定价的不同方案来做仿真分析。现在我们对于此新产品的投产再多拟定两个方案，即将新产品定价为18元或20元，再将这两个方案与定价为15元的方案作比较，同样进行仿真。这两个方案中，随着定价的改变，方案中的需求量的均值、标准方差与营销费用的投入情况也将发生改变。变化的趋势是：定价高则需求量相对较少，方差值也大，而营销费用的投入相应也要多一些。定价18元和20元的演算过程与15元定价的仿真过程一样，仿真结果如下：

由表7我们可以看出，本例中几个方案的对比结果，在现有的条件下，定价18元的方案相对比较有利。此方案亏损的风险相对较小，但获利较大。具体方案为表8：

蒙特卡洛仿真的优点是综合考虑了众多市场因素对生产计划的影响，从市场需求预测的角度出发，对产品的定价、营销费用的投入、首印数等进行了全局考虑，避免了出版社在制定生产计划时的盲目性，它能更加客观全面地描述实际系统的行为，并可以结合供应链上的不确定因素的影响，制定多种方案进行预测，在选取最佳方案保证利润最优化的前提下，为有效规避库存带来的亏损风险、合理地制定配送策略创造了条件。 （作者系广东新世纪出版社有限公司副社长）