带TMD及Maxwell阻尼器结构的随机地震响应
邹万杰,寇金鑫,李创第,葛新广
(广西科技大学土木建筑工程学院, 广西柳州545006)
带TMD及Maxwell阻尼器结构的随机地震响应
邹万杰,寇金鑫,李创第,葛新广
(广西科技大学土木建筑工程学院, 广西柳州545006)
摘要:为了对同时设置TMD及Maxwell阻尼器的建筑结构随机地震响应进行分析,将结构响应以第一振型展开,所得运动方程中质量矩阵、刚度矩阵、阻尼矩阵均非对称,故采用扩阶复模态理论对其解耦,获得了结构以第一振型表示的地震响应的解析表达式。算例分析结果表明:同时设置TMD及Maxwell阻尼器的结构比单一设置TMD或Maxwell阻尼器的减震效果更好,而且可以有效减少阻尼器的受力。
关键词:随机地震响应;扩阶复模态;TMD;Maxwell阻尼器
0前言
为减小地震作用对建筑结构的影响,多种被动控制技术(如TMD、粘滞阻尼器和粘弹性阻尼器)已广泛应用于地震响应的控制中[1-6]。TMD减震主要是通过建筑物附加TMD装置耗散地震输入的能量,以达到减小主体结构的地震反应。因其具有构造简单,经济实用,维护方便和易于安装等优点受到较多科研工作者以及工程界的关注[7]。目前,在世界各地的部分高层建筑上和高耸结构上已成功安装了TMD,比如美国纽约的Citicorp Center和波士顿的John Hancock Building。根据报道,这两栋建筑物在风荷载作用下加速度响应可降低40%[8]。粘弹性阻尼器主要通过增大原结构的刚度与阻尼来降低结构的地震响应,从而实现了建筑结构的耗能减震。其作为一种适用范围广且耗能效率高的被动控制装置,在新建建筑结构及对已有建筑结构的加固方面都有着广泛的应用,同时对于高层、高柔及大跨桥梁等结构形式有较为显著的减震效果[9-10]。我国在2010版建筑抗震规范又对耗能减震设计内容作了补充和完善[11]。
由于TMD的布置需要一定的空间,一般都布置在顶层,而粘弹性阻尼器布置较为灵活,一般设置在层间,为此研究将两者结合起来进行地震动控制具有一定的工程应用意义。本文将Maxwell耗能阻尼器及TMD同时施加在建筑结构上,利用扩阶复模态法对此类混合被动控制结构的随机地震响应问题进行了系统分析,得到了结构地震响应的解析表达式,算例分析表明其具有更加良好的减震效果。
1结构运动方程
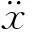
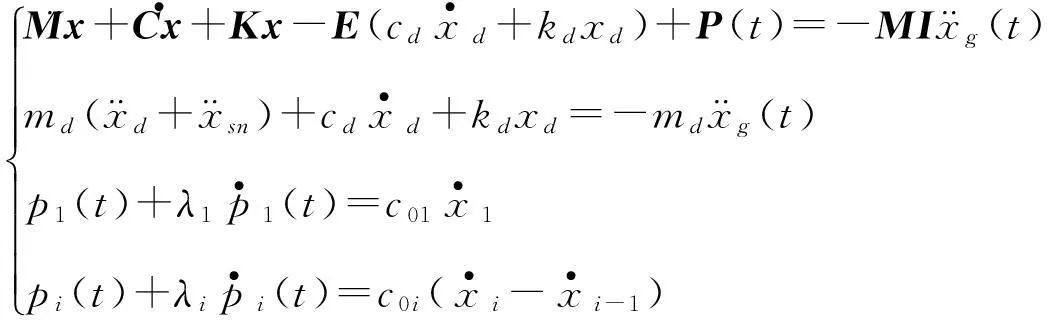
(1)
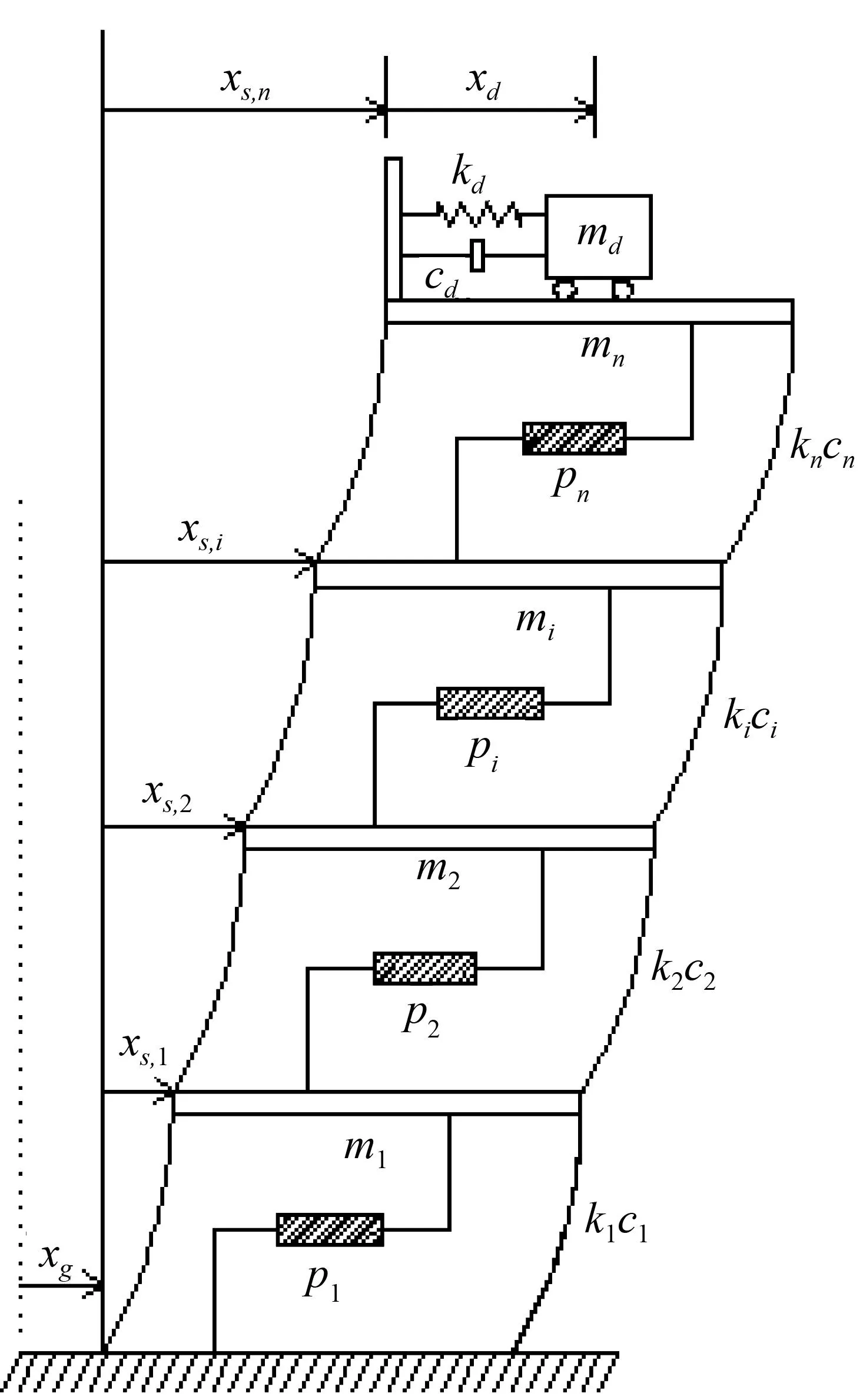
图1 计算简图Fig.1 Calculation diagram
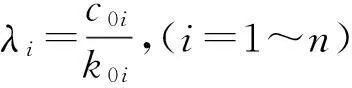
对于多高层规则的建筑结构,结构可按第一振型展开[12],令:
x=φq,
(2)
式中:φ=[φ1,φ2,…φn]T,q为第一振型对应的广义位移。
将式(2)代入运动方程(1)中并经整理后,结构的运动方程可化为以下形式:
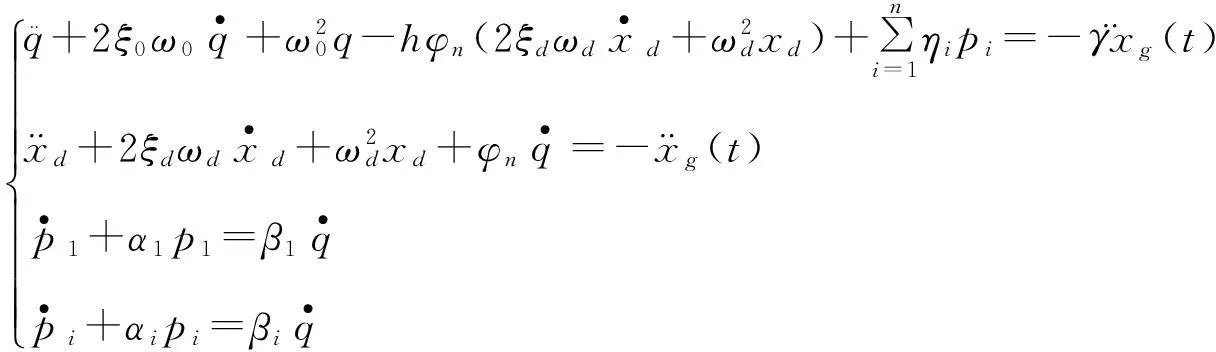
(3)
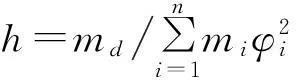
2结构响应分析
设状态变量z(t)为:
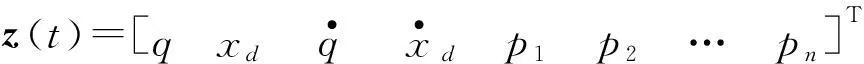
(3)
由式(3)可将原结构运动方程组化为一阶状态方程组:
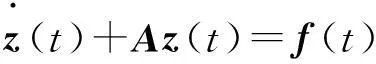
(4)
式中:
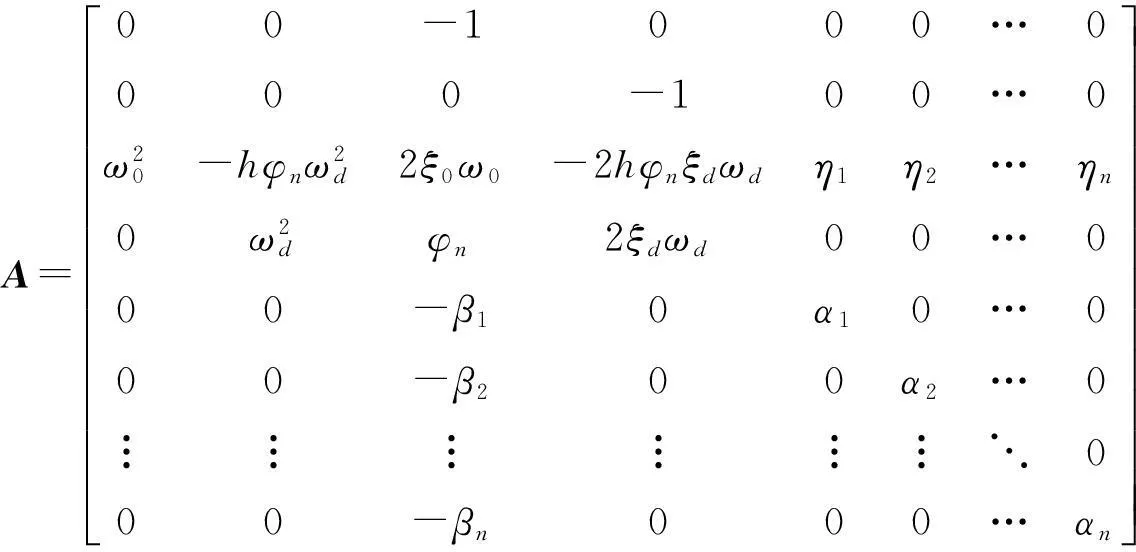

方程(4)的特征根方程为:
det[Iλj+A]=0,
(5)
即:
当n=1时,将行列式按最后一列展开,得:
当n=2时,将行列式按最后一列展开,得:
以此类推,当n=n时,特征根方程可化为:
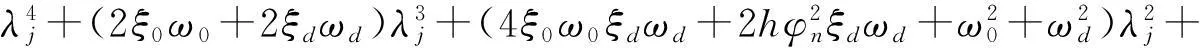

(6)
由上面所得的特征根方程可以求得的n+4个特征根λj。方程(5)的右、左复模态Uj和Vj所满足的方程分别为:
[Iλj+A]Uj=0;[Iλj+A]TVj=0,
(7)
令:
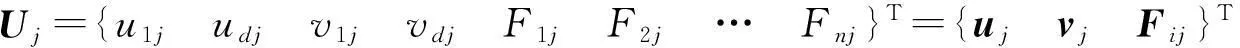
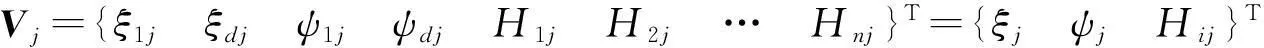
(8)
经计算可得:
根据文献复模态理论[13-16],令:
z(t)=UY(t)。
(9)
由矩阵U、V的正交性,方程(4)可化为以下形式:
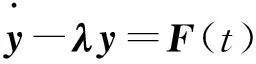
(10)
可得结构响应为:
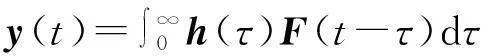
(11)

式 (11) 的分量形式为:
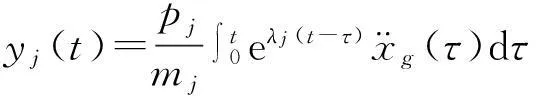
(12)
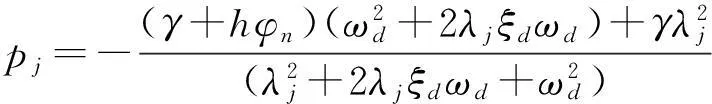
由式(11)及式(12),得结构各层的位移、速度以及TMD和Maxwell阻尼器的响应分别为:
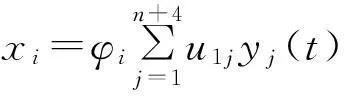
(13)
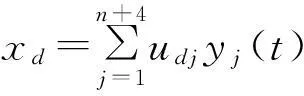
(14)
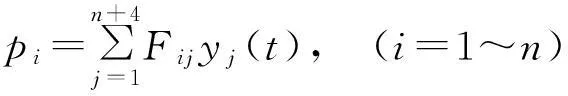
(15)
3结构响应方差分析
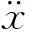
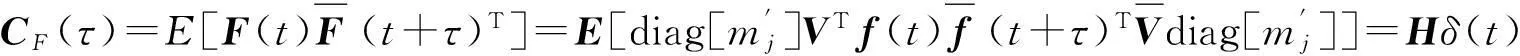
(16)
式中:
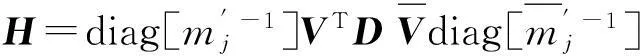
D为(n+4)×(n+4)矩阵,其中D(3,3)=γ2,D(3,4)=γ,D(4,3)=γ,D(4,4)=1,其余元素全为0。
H的分量形式为:
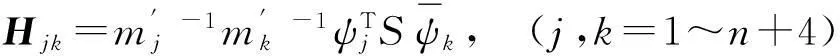
(17)
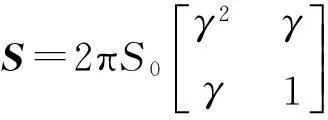
模态响应向量Y的协方差函数矩阵可表以示为:
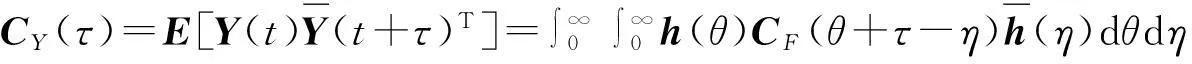
(18)
将上式展开:
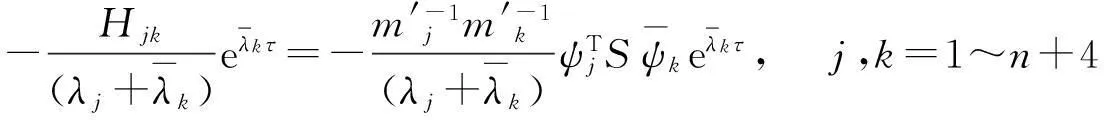
(19)
令τ=0,由式(12)、式(13)以及式(20),得结构各层的位移、速度以及TMD和Maxwell阻尼器的响应方差分别为:
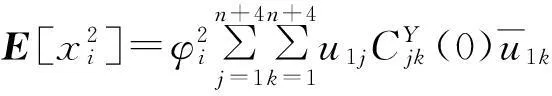
(20)
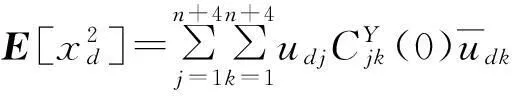
(21)
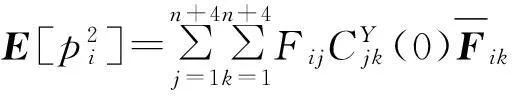
(22)
4算例
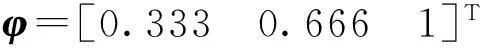

表1 结构响应方差

表2 Maxwell阻尼器受力方差
从表1可看出设置两种阻尼器结构的位移、速度响应方差均比仅设置一种阻尼器的小。以顶层为例,设置两种阻尼器的结构其位移方差相比仅设置Maxwell阻尼器和仅设置TMD 分别降低13.5%、25.6%;而速度方差分别降低19.1%、26%,说明减震效果更为显著。
从表2可看出在已施加Maxwell阻尼器的结构上再设置TMD则Maxwell阻尼器的受力方差比不设置TMD的少。以顶层为例,阻尼器的受力方差比不加TMD 的降低24.0%,说明Maxwell阻尼器的受力明显减少,更能有效的保护结构的安全。
5结语
本文对同时设置TMD及Maxwell耗能阻尼器的结构随机地震响应进行了分析。由于所对应的运动方程阻尼、质量和刚度均非对称,因此采用扩阶复模态方法进行解耦,获得了在平稳白噪声激励下结构地震响应的解析表达式,从而建立了多高层建筑结构当同时设置TMD和Maxwell两种减震装置时结构随机地震响应解析分析的一般方法。算例表明结构同时设置TMD及Maxwell阻尼器时比单一只设置TMD或Maxwell阻尼器的减震效果更好,且在Maxwell耗能结构的基础上设置TMD装置可减少Maxwell阻尼器的受力,降低了结构振动中Maxwell阻尼器先于原结构破坏的机率,进一步提高了结构的安全性。
参考文献:
[1]SOONG TT, DARGUSH G F.Passive energy dissipation systems in structural engineering[M]. England: John wiley and Ltd,1997.
[2]周云.粘弹性阻尼减震结构设计[M]. 武汉:武汉理工大学出版社,2006.
[3]周云,邓雪松,吴从晓.高层建筑耗能减震新体系概念与实现[J]. 工程抗震与加固改造,2007,29(6):1-9.
[4]欧进萍, 吴斌, 龙旭.耗能减震结构的抗震设计方法[J]. 地震工程与工程振动, 1998, 18(2): 98-107.
[5]秦丽, 李业学,徐福卫.TMD对结构地震响应控制效果的研究[J]. 世界地震工程, 2010, 26(1): 202-206.
[6]王彩华, 吴剑锋,张丽娜.用于工程结构减震控制的耗能减震技术[J]. 工程与建设, 2009, 23(3): 377-378.
[7]谭平.带TMD结构的随机地震响应分析的新方法[J]. 北京理工大学学报,2010,30(4): 390-391.
[8]LIN CC, HU C M, WANG J F, et al.Vibration control effectiveness of passive tuned mass dampers[J]. Journal of the Chinese Institute of Engineering.1994,17 (3): 367-376.
[9]李创第,黄天立,李暾,等.基础隔震结构随机地震响应分析的复模态法[J]. 地震工程与工程振动, 2002, 22(6): 122-128.
[10]蔡雪霁.基于遗传算法的粘滞阻尼减震结构的抗震优化设计[D]. 广西科技大学土木建筑工程学院, 2013.
[11]中华人民共和国国家标准.建筑抗震设计规范(GB50011-2010)[S]. 北京: 中国建筑工业出版社, 2010.
[12]WISCHING P H, YAO T P.Model response of structures[J]. Journal of structural Division,ASCE, 1970,96(4):879-882.
[13]陈欧阳.非对称非经典结构实空间解耦和地震作用取值方法及其在多高层隔震结构中应用[D]. 南宁:广西大学土木建筑工程学院, 2013.
[14]李创第, 陈欧阳, 葛新广, 等.多层隔震结构近似实空间解耦及地震作用取值[J]. 广西大学学报:自然科学版,2013, 38(4): 785-794.
[15]FANG T, WANG Z Z.Stationary response to second-order filtered white noise excitation[J]. AIAA J.1986, 24(6):1048-1051.
[16]黄东梅, 李创第, 朱乐乐.基础隔震结构基于设计反应谱的地震作用取值[J]. 西安建筑科技大学学报:自然科学版,2007, 39(4): 504-511.
(责任编辑唐汉民梁碧芬)
Random earthquake response of structure with TMD and Maxwell damper
ZOU Wan-jie, KOU Jin-xin, LI Chuang-di, GE Xin-guang
(Department of Civil Engineering, Guangxi University of Science and Technology, Liuzhou 545006, China)
Abstract:In order to analyze the random earthquake response of a structure with TMD and Maxwell damper, the vibration response of the structure is expanded into a two-degree-of-freedom movement equation by the first mode. Because the corresponding matrices of the quality, stiffness and damping are all asymmetric, the extended complex modal method is used to decouple the equation. A numerical example shows that the shock-absorbing effect of the structure equipped with TMD and Maxwell damper together is better than that of the structure only equipped with TMD or Maxwell damper, and the force of Maxwell damper can be effectively reduced.
Key words:random earthquake response; extended complex modal method; TMD; Maxwell damper
中图分类号:TU313.3
文献标识码:A
文章编号:1001-7445(2015)06-1352-07
doi:10.13624/j.cnki.issn.1001-7445.2015.1352
通讯作者:邹万杰(1974—),男,广西蒙山人,广西科技大学副教授,博士; E-mail:705450818@qq.com。
基金项目:广西自然科学基金资助项目(2011GXNSFA018032)
收稿日期:2015-10-19;
修订日期:2015-11-01

