离散非线性系统的有限时间控制

孟晓玲，王战伟，毛北行

(郑州航空工业管理学院数理系， 河南　郑州　450015)



离散非线性系统的有限时间控制

孟晓玲，王战伟，毛北行

(郑州航空工业管理学院数理系， 河南郑州450015)

[摘要]本文针对一类离散非线性系统的有限时间控制问题，利用线性矩阵不等式以及有限时间有界的概念，给出了离散非线性系统有限时间有界的充分性条件.

[关键词]有限时间；稳定；有界

在实际工程中，常常要求控制系统的轨迹不超出一定的界限.该问题引起了众多学者的关注[1-6].文献[7]讨论了两类不确定线性系统的有限时间控制问题，并将问题的可解性归结为线性矩阵不等式.文献[8]研究了离散奇异系统的有限时间控制问题.文献[9]研究了一类不确定线性离散系统有限时间观测器设计.本文针对一类离散非线性系统的有限时间控制问题，给出了离散非线性系统有限时间有界的充分性条件.

1主要结果

考虑如下离散非线性系统

x(k+1)=Ax(k)+Bu(k)+f(x(k))

(1)

假设1非线性函数f(x(k))满足条件：‖f(x(k))‖≤l‖x(k)‖，其中l为大于零的常数.

定义1给定正数δ,ε，且δ<ε，以及N∈N+，正定矩阵R，系统(1)关于(δ,ε,R,N)称为有限时间稳定的，若：

xT(0)Rx(0)≤δ2⟹xT(k)Rx(k)<ε2,

∀k∈{1,2,…,N} .

考虑如下带有扰动的系统

x(k+1)=Ax(k)+Bu(k)+f(x(k))+ω(k)

(2)

ω(k+1)=Fω(k)

(3)

定义2给定正数δ、ε、d，且δ<ε以及N∈N+，正定矩阵R，系统(2)、(3)关于(δ,ε,R,N,d)称为有限时间有界的，若：

xT(0)Rx(0)≤δ2⟹xT(k)Rx(k)<ε2,

∀ω(k):ωT(k)ω(k)≤d，∀k∈{1,2,…,N}

1)s<0；

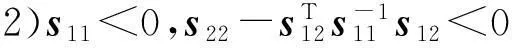
定理1系统(1)关于(δ,ε,R,N)称为有限时间稳定的，若存在对称正定矩阵P，及反馈控制律u(k)=Kx(k)，使得下列不等式成立：

(A + BK)TP(A +BK) + (l2-1)P +

l[(A +BK)TP +P(A +BK)]≤0

(4)

(5)

证明构造Lyapunov函数V(x(k))=xT(k)Px(k),则有：

V(x(k+1))-V(x(k))

=xT(k+1)Px(k+1)-xT(k)Px(k)

=[(A +BK)x(k) +f(x(k))]TP[(A +BK)×

x(k) +f(x(k))]-xT(k)Px(k)

≤xT(k){(A+BK)TP(A+BK)+(l2-1)P+

l[(A+BK)TP+P(A+BK)]}x(k)

由(4)可知

V(k+1)-V(k)≤0

(6)

对(6)从0到k-1求和，可得V(k)-V(0)≤0即:

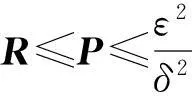
xT(k)Px(k)≤xT(0)Px(0)⟹

xT(k)Rx(k)≤xT(k)Px(k)≤

若

xT(0)Rx(0)≤δ2⟹xT(k)Rx(k)<ε2，

从而系统(1)关于(δ,ε,R,N)称为有限时间稳定的.

定理2系统(1)是可解的，若存在对称正定矩阵P，及反馈控制律u(k)=Kx(k)，使得下列不等式成立：

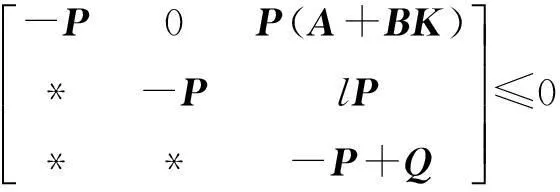
(7)

其中：Q=l[(A+BK)TP+P(A+BK)].

证明由定理1可知系统(1)关于(δ,ε,R,N)称为有限时间稳定的充分条件为：

(A+BK)TP(A+BK)+(l2-1)P+

l[(A+BK)TP+P(A+BK)]≤0

(8)

对(8)利用引理1，得到(8)等价于如下矩阵不等式：

(9)

很容易得到(7).

定理3系统(2)、(3)关于(δ,ε,R,N,d)称为有限时间有界的，若存在对称正定矩阵P、Q及反馈控制律u(k)=Kx(k)，使得下列不等式成立：

(10)

P≤R

(11)

δ2+λmax(Q)d<ε2

(12)

Ω1=(A+BK)TP(A+BK)+(l2-1)P+

l[(A+BK)TP+P(A+BK)]

Ω2=FTQF-Q+P，I为适当维数的单位矩阵.

证明构造Lyapunov函数

V(x(k))=xT(k)Px(k)+ωT(k)Qω(k),

则

V(x(k+1))-V(x(k))

=xT(k+1)Px(k+1)+

ωT(k+1)Qω(k+1)-xT(k)Px(k)-ωT(k)Qω(k)

≤[(A +BK)x(k) +f(x(k)) + ω(k)]T

P[(A+BK)x(k) +f(x(k)) +ω(k)]

-xT(k)Px(k) +ωT(k)(FTQF-Q)ω(k)

≤0

由(10)可知

V(k+1)-V(k)≤0

(13)

对(13)从0到k-1求和，可得V(k)-V(0)≤0，即：

xT(k)Px(k) + ωT(k)Qω(k)

≤xT(k)Rx(k) + ωT(k)Qω(k)

≤xT(0)Rx(0) + ωT(0)Qω(0)

≤δ2+λmax(Q)d

若

xT(0)Rx(0)≤δ2⟹

xT(k)Rx(k)≤δ2+λmax(Q)d<ε2，

从而满足定义2.

2结论

本文针对一类离散非线性系统的有限时间控制问题，得到了系统有限时间有界的条件，结论以线性矩阵不等式形式给出，便于利用Matlab求解.该问题的有限时间混沌同步是需要进一步研究的课题.

[参考文献]

[1]AmatoF，AriolaM，CosentinoC，eta1．Necessaryandsufficientconditionsforfinite-timestabilityoflinearsystems[C]．2003AmericanControlConference，IEEEPress：2003(5)：4452-4456．

[2]AmatoF，AriolaM，Cosentino.Controloflineardiscrete-timesystemsoverafinite-timeinterval[C]．43rdIEEEConferenceonDecisionandControl，Atlantis：IEEEPress：2004(2)：1284-1288．

[3]AmatoF．Finite-timecontrolofdiscrete-timelinearsystem[J].IEEETransAutomatControl，2005，50(5)：724-729．

[4]DoratoP．Shorttimestabilityinlineartimevaryingsystem[C]．IRElnternationalConventionRecordPart4，1961：83-87．

[5]AmatoF，AriolaM，AbdallahCT，etal.Dynamicoutputfeedbackfinite-timecontrolofLTIsystemssubjecttoparametricuncertaintiesanddisturbances[C]．EuropeanControlConference,Kals-mhe，1999：1176-1180．

[6]AmatoF，AroliaM，DoratoP．Statefeedbackstabilizationoverafinite-timeintervaloflinearsystemssubjecttonormboundedparametricuncertainties[C]．The36thAllertonConference，Monticello：1998．

[7]AmatoF，AroliaM，DobatoP．Finite-timecontroloflinearsystemssubjecttoparametricuncertaintiesanddisturbance[J]．Automatic，2001，37：1459-1463．

[8]黄发，吴保卫.离散奇异系统的有限时间控制[J].重庆师范大学学报：自然科学版，2012,29(2)：51-54.

[9]朱琳，沈艳军. 一类不确定线性离散系统有限时间观测器设计[J].电机与控制学报，2008,12(1)：99-108.

[10]俞立. 鲁棒控制——线性矩阵不等式处理方法[M].北京：清华大学出版社，2002.

(责任编辑穆刚)

Finite-time control of discrete-time nonlinear system

MENG Xiaoling, WANG Zhanwei, MAO Beixing

(Department of Mathematics and Physics, Zhengzhou Institute of Aeronautical Industry Management, Zhengzhou He’nan 450015, China)

Abstract：The paper deals with the problem of finite-time control for one kind of nonlinear discrete systems. Using LMI and finite-time bounded conception the sufficient conditions of finite-time control were obtained.

Key words：finite-time; stable; bounded

[中图分类号]O482.4

[文献标志码]A

[文章编号]1673-8004(2015)05-0030-03

[作者简介]孟晓玲 (1976—)，女，安徽安庆人，讲师，硕士，主要从事复杂网络与混沌同步方面的研究.

[基金项目]国家自然科学基金项目(51072184)；国家自然科学基金数学天元基金项目(11226337)；航空基金项目(2013ZD55006)；河南省高等学校青年骨干教师资助计划项目(2013GGJS-142)；郑州航空工业管理学院青年基金项目(2014113002)；河南省高等学校重点科研项目(15B110011).

[收稿日期]2014-11-05