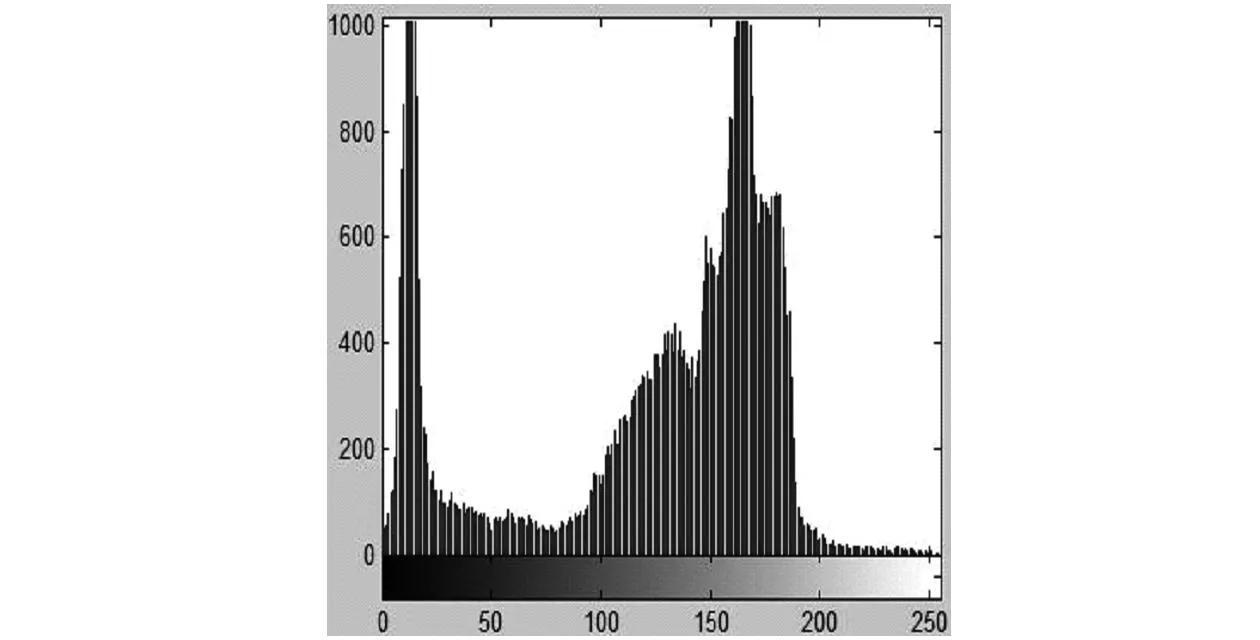
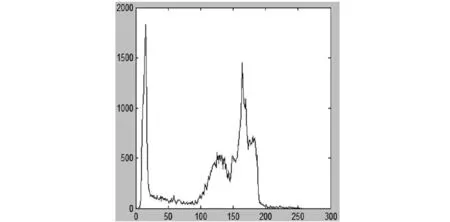
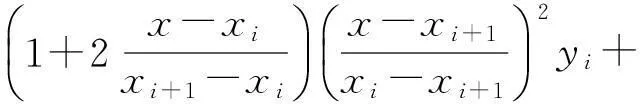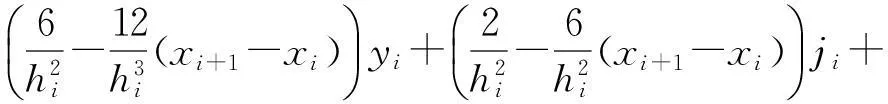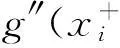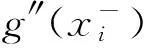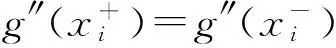基于样条插值的图像分割算法研究

程东旭， 杜娅丽

(中原工学院, 郑州 450007)

基于样条插值的图像分割算法研究

程东旭， 杜娅丽

(中原工学院, 郑州 450007)

摘要：针对传统分割算法中的阈值选择问题，提出了一种改进的图像阈值分割算法。采用样条插值方法对图像的灰度直方图进行曲线拟合，获得直方图的曲线表达。利用函数极值的特点寻找直方图曲线的极值点，获取阈值，对图像进行阈值分割。实验结果表明，改进算法获得的阈值较其他算法有更好的分割效果。

关键词：阈值分割;直方图;曲线拟合;样条插值

图像分割是图像处理领域的一个重要组成部分，分割效果直接影响图像分析、模式识别等。图像分割算法有两类：传统图像分割算法和现代图像分割算法[1]。前者有双峰法、迭代法、Otsu法等，后者有多种方法，大多数是将一些特定理论的研究成果运用到图像分割中，如：数学形态学、遗传算法理论、模糊理论、小波变换理论等，是针对特殊的图像结合特定的数学方法进行分割的先进图像分割技术。

本文在阈值分割算法的基础上，提出一种基于样条插值的现代图像分割算法。首先利用样条插值拟合图像的直方图，获得直方图的曲线表达式；再利用函数极值的特点寻找直方图曲线的极值点，获取阈值，对图像进行阈值分割。

该方法的特点：①适用于所有具有波峰、波谷的图像，克服了传统算法的不足；②根据阈值多位于直方图波谷位置的特点，巧妙利用函数极值的特点寻找直方图曲线的极值点，获取阈值；③与传统的分割方法相比，具有计算简单、运算效率高以及速度快等特点，并且所得结果更加准确，分割效果更好。

1图像分割原理与算法

1.1图像分割基本原理

1.1.1灰度阈值分割方法

灰度阈值分割方法是输入图像g到输出图像k变换的一种方式，变换表达式为：

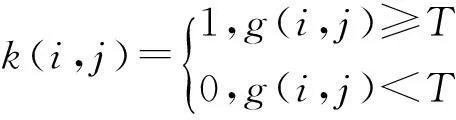
(1)

其中：T为阈值；目标物体像素k(i,j)=1；背景像素k(i,j)=0。

上述方法是图像分割中最常用的算法，具有计算简单、运算效率高、速度快等优点[2]。其关键是阈值的确定，合适的阈值可准确地分割图像。

1.1.2区域生长分割方法

区域生长算法是集合所有具有相似性质的像素构成区域。具体为：找一个种子像素作为每个需要分割的区域生长的起点；合并种子像素周围与种子像素具有相似或者相同性质的像素，形成新的种子像素；继续训练这些新像素，直到再也没有像素可被合并为止，从而生成一个区域[3]。

区域生长分割方法的优点在于计算简单，对较均匀的连通目标进行分割具有较好的效果。它的缺点就是对噪声比较敏感，种子点需要人为地加以确定，还有可能会导致区域内空洞；另外，它是串行算法，当需要分割的目标比较大时，分割速度比较慢。

1.2传统图像分割算法

1.2.1双峰法

双峰法适用于以下图像中：要分割图像的灰度直方图分布比较有规律；图像背景和分割目标区域的灰度各自形成一个波峰，满足波峰与区域一一对应。其分离思想为：将对应在双峰间的波谷处的灰度值作为阈值，即可将图像背景中有意义的部分分割出来[4]。

该方法的缺点为：当双峰间出现波谷比较平坦或图像灰度直方图波形不明显等情况时，使用该方法难以确定阈值，需采用其他方法才能完成阈值选择。

1.2.2迭代法

迭代法选取阈值的基本思想是利用程序自动搜寻最合适的阈值。具体为：初始值T0是图像灰度的中值，图像全部的像素被分为前景和背景；将积分后的结果取平均值作为新的阈值，按此阈值再次将图像分为前景和背景；反复迭代下去，直到阈值不再变化为止，将此时的阈值作为最终的结果并运用于图像分割[5]。迭代公式如下：

(2)

其中：灰度级的个数为L；灰度值k的像素点的个数为lk。当Ti+1=Ti时，迭代结束，Ti即为阈值。

1.2.3Otsu法

Otsu法适用于图像灰度直方图有双峰但无低谷或双峰与低谷都不明显的图像。它将图像灰度值分成两类，最佳阈值为类间方差与类内方差分离度最大时的灰度值。

同一区域具有相似的灰度特性，不同区域灰度差异明显，当两个区域之间灰度差较大时，两个区域的平均灰度u1、u2与整个图像的平均灰度u之差也较大[6]。

该方法的特点：对图像二值化时准确而快速，当图像分割目标和背景的灰度值差距比较大时，效果更加明显。

2基于样条插值的阈值分割算法

2.1样条插值

设在区间[m,n]内插入k-1个节点，即:

m=x0

构造一个三次样条插值函数g(x)。

已知：

(1)节点处的函数值为：

f(xi)=yi(i=0,1,…,k)

(2)三次样条插值函数g(x)满足以下3个条件：

(a)g(xi)=yi(i=0,1,2,…，k)；

(b)g(x)在每一个小区间[xi,xi+1]上是一个三次多项表达式；

(c)g(x)∈C2[m,n]。

求解过程如下：

假设区间[m,n]上三次样条插值函数g(x)存在，用ji表示g(x)在点xi处的微商，曲线通过点(xi,yi)(i=0,1,2,…,n)，且在每一个小区间[xi,xi+1]上满足以下条件：

g(xi)=yi, g(xi+1)=yi+1

(3)

g′(xi)=ji, g′(xi+1)=ji+1

(4)

利用Hermite插值公式写出小区间[xi,xi+1]上的样条插值函数g(x)的表达式：

(5)

但是在节点xi(i=0,1,2,…,k)上的微商ji未知，如果要用表达式(5)，必须设法求出(j0,j1,…,jk)的值。利用函数g(x)在节点xi上的二阶微商连续的性质，将上述表达式对x求微商，同时令hi=xi+1-x，得到以下表达式：

(6)

(7)

(9)

令

(10)

在每个内点建立方程，则得到下列方程组:

(1-αi)ji-1+2ji+αiji+1=βi(i=1,2,…,k-1)

(11)

这是关于未知数(j0,ji,…,jk)的k-1个线性方程组。这个方程组会有无穷多个解，但是实际问题是只能选取一个特定的解。因此根据具体情况，补充两个附加条件，假设曲线在两个端点处的二阶微商已知,

令y″0=y″n=0,或g″(x0)=g″(xk)=0，可得：

(12)

将式(12)与式(11)联立，可以解出唯一的未知数(j0,j1,…,jk)。

将求得的ji代入公式(5)中，求出区间[xi,xi+1]上的样条插值函数g(xi) (i=0,1,2,…,k-1)。

采用样条插值得出插值函数，当插值节点加密时，插值函数收敛于它本身，其微商收敛于函数的微商，其结果比多项式插值得到的结果更优越。从图1、图2可以看出，采用该方法得出的拟合曲线与原图像的直方图非常接近。

2.2基于三次样条插值的阈值选取算法

首先，在得到图像的灰度直方图的基础上，为了使图像灰度值更加具有连续性，采用三次样条插值方法拟合图像灰度曲线，根据所得到的图像灰度曲线，找到阈值所在的灰度区间。这一步主要是为了更加准确地寻找阈值分割点，缩小阈值所在的区间范围。

其次，截取阈值所在区间，采用三次样条插值方法有针对性地再次进行曲线拟合。

最后，寻找曲线的极值点。本文主要采用逐步差分的方法来计算拟合曲线的极小值点。当该点左边的差值为正，右边差值为负的时候，该点为极小值点，即图像像素明显变化的点。用该点作为阈值，将大于该点的像素点设为1，小于该点的像素点设为0，从而将图像分割出来。

2.3基于三次样条插值的阈值图像分割

采用三次样条插值方法拟合图像灰度直方图曲线，找到图像像素明显变化的区域，提取该区间，再次进行三次样条插值，进一步拟合图像灰度曲线。采用差分的方法找到该区域的极小值点，确定该极小值点为阈值点。

具体步骤如下：

(1)读取将要分割的图像，如果是彩色图像，先将彩色图像转化为灰度图像；

(2)对图像进行中值滤波，减少噪声对图像分割的影响；

(3)计算该图像的灰度值，画出图像的灰度直方图，如图1所示。

图1　图像灰度直方图

(4)利用Matlab编程进行三次样条插值拟合，拟合出图像的灰度曲线，查看图像灰度曲线的波动情况，确定阈值所在的区间。截取这一区间，采用三次样条插值方法有针对性地再次进行曲线拟合。三次样条插值拟合图像灰度曲线如图2所示。

图2　样条插值拟合曲线

(5)采用差分的方法寻找曲线的极值点。编写循环语句，当找到满足条件的点时，终止程序运行，输出该点的灰度值作为阈值，将图像的灰度转化到[0,1]之间，从而完成图像的分割。

2.4实验结果

采用经典传统方法中的双峰法、迭代法、Otsu法分别进行图像分割，与本文采用三次样条插值方法选取阈值进行图像分割的结果进行对比(如图3所示),结果发现采用三次样条插值选取阈值的方法具有很大的优越性。

(a)双峰法　　　　　　　　(b)迭代法

(c)Otsu法　　　　　　　(d)三次样条插值法图3　图像分割结果对比

3结语

经过与经典传统分割方法对比发现，三次样条插

值函数收敛于函数本身，而且其微商也收敛于函数的微商。采用三次样条插值方法选取阈值更加准确，分割效果更好，并且计算简单、运算效率高、速度快。

综合本次图像分割的实现方法以及分割效果，该分割方法还存在一些不足，如一些参数设置不够优化，导致分割效果不是特别理想。随后的研究可以将算法进行优化，并结合其他图片进行分析，将三次样条插值选取阈值方法做得更加完善。

参考文献:

[1]徐瑞.图像分割方法及性能评价综述[J].宁波工程学院学报,2011,23(3):76-79.

[2]何俊,葛红,王玉峰.图像分割算法研究综述[J].计算机工程与科学，2009,31(12)：58-61.

[3]魏津瑜,施鹤南,苏思沁.基于改进算法的自动种子区域生长图像分割[J].中南大学学报(自然科学版)，2013(s2):311-315.

[4]余松煜，周源华，张瑞.数字图像处理[M].上海：上海交通大学出版社，2007.

[5]陈宁宁.几种图像阈值分割算法的实现与比较[J].人工智能及识别技术, 2011, 7(13): 3109-3111.

[6]郭永芳,于明,黄凯.基于细菌趋药性的Otsu双阈值图像分割算法[J].计算机工程,2011, 37(22):8-11.

(责任编辑：席艳君)

Image Segmentation Algorithm Study Based on Spline Interpolation

CHENG Dong-xu, DU Ya-li

(Zhongyuan University of Technology, Zhengzhou 450007, China)

Abstract:In order to solve the threshold selection problem of the traditional segmentation algorithms, an improved spline interpolation algorithm for image segmentation is presented. Firstly, the spline interpolation is used to obtain the image histogram fitting curve. Secondly, the extreme points of the histogram curve is found based on the characteristic of the function extreme and the threshold is obtained. Then, the image is segmented with the threshold. Numerical experiments show that the threshold segmentation obtained by the improved algorithm is better than other algorithms.

Key words:threshold segmentation; histogram; curve fitting;spline interpolation

文章编号：1671-6906(2015)01-0013-04

作者简介：杨艳(1982-)，女，河南济源人，硕士，讲师。

基金项目：国家自然科学基金数学天元基金(11326167)；河南省高等学校重点科研项目(15A110045)

收稿日期：2014-03-21

中图分类号：TG142.1

文献标志码：ADOI:10.3969/j.issn.1671-6906.2015.01.003