基于Gauss曲率的医学超声图像去噪算法研究

杨　艳， 孙　俊, 程东旭

(中原工学院, 郑州 450007)

基于Gauss曲率的医学超声图像去噪算法研究

杨艳， 孙俊, 程东旭

(中原工学院, 郑州 450007)

摘要：针对医学超声图像清晰度低，易受乘性噪声污染等问题，提出了一种基于Gauss曲率的超声图像去噪算法，并构造一种Gauss曲率扩散函数，自适应控制扩散速度，克服了传统去噪算法不能保护弱边缘的缺点。根据变分法得到Euler-Lagrange方程，给出一种计算平衡系数的方法，并引入图像差异范数作为终止迭代准则。数值实验仿真结果显示，该算法能够有效去除医学超声图像中的噪声，较好地保留超声图像中大量存在的弱边缘信息，本算法的PSNR比传统算法提高了大约4 dB。

关键词：高斯曲率； 医学超声图像； 各向异性扩散； 乘性噪声

受设备环境等外界因素的影响，医学超声图像在获取过程中不可避免地会受到噪声的干扰，使得图像质量降低，影响图像的进一步处理(如图像边缘信息的检测、图像的分割、图像特征的提取、图像表示以及进一步的理解和识别等)，从而影响病情的诊断，耽误治疗。医学超声图像中的噪声主要是乘性噪声，传统的各向异性扩散PDE算法主要是针对加性噪声，去除乘性噪声的效果不好。因此，如何去除医学超声图像中的乘性噪声成为医学超声图像处理的研究热点。

2003年Rudin L等首次提出了去除乘性噪声的全变差算法(RLO)[1]。之后，Aubert G等建立了基于最大后验概率估计的AA算法[2-3]，在此基础上，Huang Y M等和Jin Z M等分别提出了严格凸的HNW算法[4]和JY算法[5]。这些算法的主导思想都是对乘性噪声进行对数变换之后看作加性噪声处理。利用对数变换能保留图像细节、噪声以及边缘等图像信息之间差别的性质，达到去除乘性噪声的目的。但对数变换又缩小了它们之间的差异，使得小边缘与弱噪声之间的差异化更小，再采用传统的全变差方法进行去噪则会影响去噪效果，模糊边缘信息。针对以上不足和医学超声图像的特点，本文提出了一种基于Gauss曲率[6-7]的去除医学超声图像噪声算法，将传统的全变差算法改为Gauss曲率驱动算法，并提出了一种自适应的平衡参数选择算法，快速去除医学超声图像中的噪声，同时保护图像边缘等信息。

1基于全变差的去噪算法

常见的乘性噪声算法可假设为

g=uv

(1)

其中:g为含噪图像；u为原始图像；v为乘性噪声。假设噪声v服从均值为1的Gamma分布，其概率密度函数为：

(2)

这里Γ(L)为Gamma函数，由Gamma分布的性质可知乘性噪声的方差为1/L。

Rudin L等于2003年提出一种去除乘性噪声的RLO算法[1]：

(3)

(4)

由于算法(4)中的目标函数并不总是非凸的，从而难以得到全局最优解。为了克服这一不足，引入变量z(x)=logu(x),构造对数函数来代替原始图像。Jin Z M等提出JY算法[5]:

(5)

由于(z(x)+g(x)e-z(x))关于z(x)的二阶导数g(x)e-z(x)总大于0，故该算法为严格凸的。在求解之后，采用指数变换u=ez(x)恢复图像即可。

上述各算法都是对传统去除加性噪声的全变差算法的推广，采用∫Ω|u(x)|dx或∫Ω|z(x)|dx作为正则项，扩散速度依赖于像素点的梯度幅值，受偶然性因素影响较大。

2基于Gauss曲率的自适应全变分算法

2.1算法提出

基于RLO算法、AA算法以及JY算法等的不足，本文构造一种基于Gauss曲率[6-7]的去噪声算法，将图像看作z=u(x,y)的曲面，则Gauss曲率定义为:

(6)

将Gauss曲率引入JY算法，构造最小能量泛函为:

(7)

其中,kG为Gauss曲率；φ(·)为单调不减的非负函数，且满足φ(0)=0,用来控制扩散速度；λ为平衡系数；∫Ω[z(x)+g(x)e-z(x)]dx为保真项。

由于Gauss曲率为最大主曲率和最小主曲率的乘积，因此在任何一个主曲率为0的区域都取0。在穿越锐利边缘方向最大主曲率很大，而沿着锐利边缘方向最小主曲率为0，从而Gauss曲率为0。因此Gauss曲率算法能很好地保持锐利边缘。去除乘性噪声多采用对数变换方法，将噪声算法g=uv转化为logg=logu+logv，再利用去除加性噪声的思想来去除乘性噪声。对数变换虽然能够保持边缘，但同时也不可避免地会弱化边缘，尤其是本身就具有较小梯度幅值的图像特征信息，通过变换后会更加不明显。基于梯度的算法很容易忽略此微弱边缘信息，而Gauss曲率却能较好地保持这些信息。

为了获得更好的去噪效果，提出一种新的扩散函数：

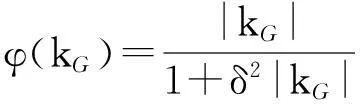
(8)

其中：δ2为对数图像z(x,y)的方差。

2.2算法求解

(9)

对(9)式采用最速下降法求解，得到扩散方程

全面提升基层党员干部的统战工作能力和水平，必须实现党员干部教育培训机制与统战教育培训体系的无缝对接，构建系统完善、科学管用的领导干部统战教育培训体系。系统的教育培训，既解决思想认识不到位的问题，又解决工作方法不专业的问题。

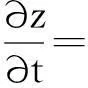
(10)

对于平衡系数λ的计算，在(9)式两端同时乘以(g(x)e-z(x)-1)，再在Ω上积分可得:

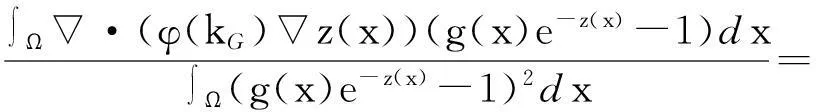
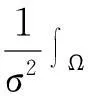
(11)

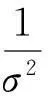
对(10)式采用差分格式进行迭代求解:

z(m+1)=z(m)+△t[(φ(m)(kG)z(n))+λ(g(m)e-z(m)-1)]

(12)

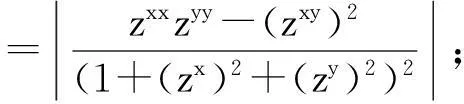
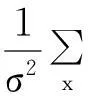
((g(x)e-z(x))(m)-1)

(13)

为了控制迭代次数，引入图像范数的概念，称‖z(x)‖2为图像z(x)的范数，‖z(x)-u(x)‖2为图像z(x)与u(x)的差异范数。

综上分析，给出本文改进算法步骤如下：

Step1：初始迭代次数m=1，最大迭代次数lmax，终止误差ε。时间步长Δt，获取观察图像数据g，令u(1)=g,z(1)=logu(1)；

Step2：利用(13)式计算λ(m)；

Step3：利用(12)式计算z(m+1)；

Step5：利用u(m)=ez(m)，计算得到恢复图像。

3数值仿真实验

对本文算法采用医学超声图像进行仿真实验，在原始图像中加入均值为1、方差为10的Gamma噪声，分别利用RLO算法、AA算法、JY算法和本文算法进行去噪，实验结果如图1所示。

由仿真结果图可以看出，本文算法在保证去噪效果的同时，可以更多地保留一些弱边缘信息，恢复图像与原始图像更加逼近。为了客观描述实验效果，计算各去噪算法效果的PSNR(峰值信噪比)，数据如表1所示。

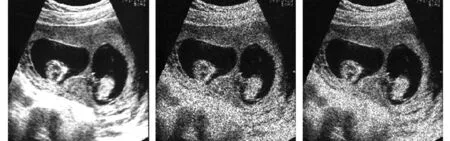
(a)原始图像　　　　　　　　　　　(b)含噪图像　　　　　　　　　　　(c)RLO算法

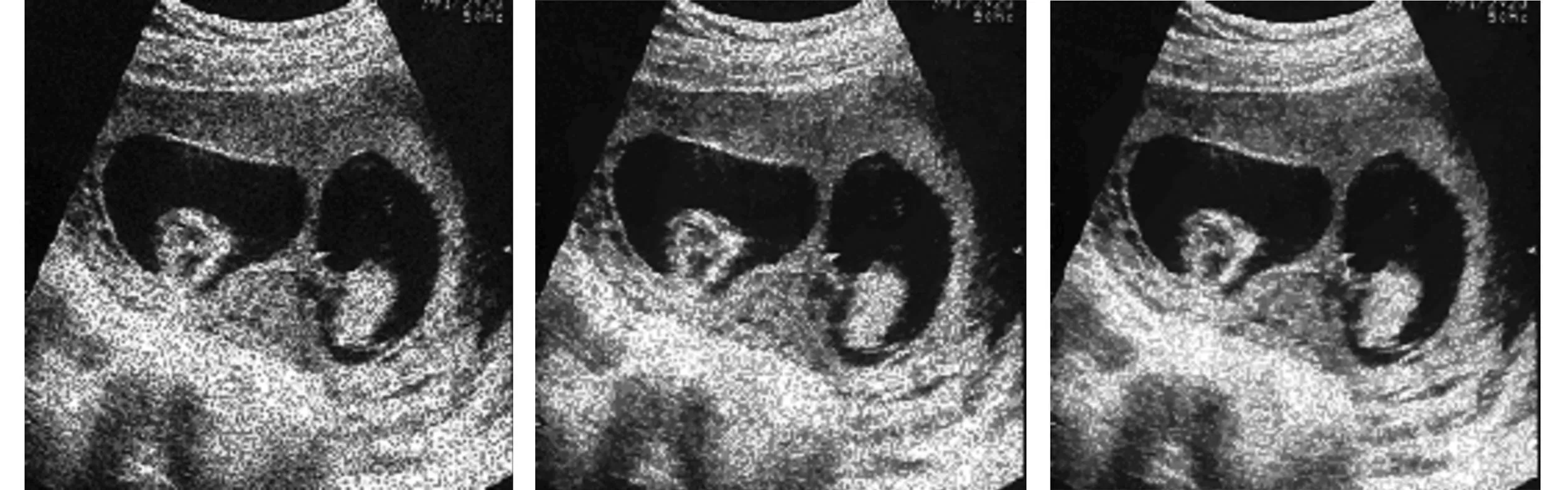
(d)AA算法　　　　　　　　　　　　(e)JY算法　　　　　　　　　　　　(f)本文算法图1　原始图像、含噪图像与各种算法去噪结果

表1　各种去噪算法的PSNR比较

由表1可知本文算法的PSNR数据最大，这与图1所示结果是一致的。

4结语

针对医学超声图像MRI图像中噪声的特点，分析了经典的RLO算法、AA算法和JY算法的不足，利用Gauss曲率所具备的优点，构造一种基于Gauss曲率的各向异性扩散去噪算法。通过数值实验仿真可知，本文算法在医学超声图像去噪方面效果较好，并能有效保护图像中的弱边缘，有利于医学超声图像的后续处理。

参考文献:

[1]Rudin L, Lions P L, Osher S. Multiplicative Denoising and Deblurring: Theory and Algorithms[M]. New York: Springer, 2003: 103-119.

[2]Aubert G, Aujol J. A Nonconvex Model to Remove Multiplicative Noise[C]//Proceedings of the 1st International Conference on Scale Space and Variational Methods in Computer Vision. Italy: Springer, 2007： 68-79.

[3]Aubert G, Aujol J. A Variational Approach to Removing Multipli-cative Noise[J].SIAM Journal on Applied Mathematics, 2008, 68(4): 925-946.

[4]Huang Y M, Ng M K, Wen Y W. A New Total Variation Method for Multiplicative Noise Removal[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 20-40.

[5]Jin Z M, Yang X P. Analysis of a New Variational Model for Multiplicative Noise Removal[J]. Journal of Mathematical Analysis and Applications, 2010, 362(2): 415-426.

[6]Suk H L,Jin K S. Noise Removal with Gauss Curvature-driven Diffusion[J].IEEE Transactions on Image Processing, 2005, 14(7): 904-909.

[7]Firsov D, Lui S H. Domain Decomposition Methods in Image Denoising Using Gaussian Curvature[J].Journal of Computational and Applied Mathematics, 2006, 193(2): 460-473.

(责任编辑：姜海芹)

Denoising Algorithm of Medical Ultrasound Image Based on Gauss Curvature

YANG Yan, SUN Jun, CHENG Dong-xu

(Zhongyuan University of Technology, Zhengzhou 450007, China)

Abstract：A medical ultrasound image denoising algorithm based on the gauss curvature is proposed according to the medical ultrasound image characteristics which have low definition and is vulnerable to be polluted by the multiplicative noise. A new Gauss curvature diffusion function is constructed and the diffusion velocity can be controlled adaptively. It overcomes the shortcoming that the traditional denoising algorithm can not protect the weak edges. A method of calculating equilibrium coefficient is presented based on the Euler-Lagrange equation which is obtained by the variation method. The image difference norm is introduced as the iteration stopping criterion. Numerical simulation results show that the new algorithm can remove the noise in medical ultrasound image effectively and retain the weak edge information exist in the ultrasound image. The experimental data shows that the PSNR of the new algorithm is about 4dB higher than the traditional algorithms.

Key words:Gauss curvature; medical ultrasound image；anisotropic diffusion; multiplicative noise

文章编号：1671-6906(2015)01-0017-05

作者简介：巫付专(1965-)，男，河南安阳人，教授，研究方向为电力电子与电力传动及电能质量调节。

基金项目：河南省教育厅科学技术研究重点项目(13B470299)

收稿日期：2014-03-26

中图分类号：TP391

文献标志码：ADOI:10.3969/j.issn.1671-6906.2015.01.004