一般函数的计算机病毒模型最优控制

孙德顺，苏永美

(北京科技大学 数理学院,北京 100083)

一般函数的计算机病毒模型最优控制

孙德顺，苏永美

(北京科技大学 数理学院,北京 100083)

摘要：研究一类改进的一般函数的计算机病毒模型，并引入杀毒软件作为系统的控制变量，应用极小值原理，得到一个时变的最优控制策略。时变的控制策略不但能够使得购买杀毒软件及其更新的费用最小,而且能将被感染的计算机的数目降到最低。数值模拟显示：在控制的这段时间内，并不需要一直保持最大的效力。

关键词：计算机病毒;一般函数;最优控制;数值模拟

基金项目：国家自然科学基金项目(61074192,11101028)

作者简介：孙德顺(1990-),男,山东临沂人,硕士生;苏永美(1971-),女,山东临沂人,副教授,博士,硕士生导师,主要从事常微分方程定性与稳定性分析,生物数学模型、计算机模型的最优控制方面的研究.

收稿日期：2014-09-05

文章编号：1672-6871(2015)02-0096-04

中图分类号：O175.12

文献标志码：志码：A

0引言

计算机病毒通过各种渠道，从已被感染的计算机扩散到未被感染的计算机,其破坏性及传染性对社会造成极大的伤害，仅2008年，计算机病毒在全球造成的经济损失就高达85亿美元。考虑到计算机病毒和生物学病毒[1-3]有很高的相似性，相应的计算机病毒模型[4-8]被提出，通过研究其动力学特性，从而找到能有效控制病毒在网络中传播的方法。

自极小值原理被提出以来，最优控制理论得到了极大的发展，在控制生物学病毒的传播上得到了广泛的应用，但是在计算机病毒最优控制方面却研究的很少。文献[9-10]利用控制理论研究计算机病毒模型，但都是基于双线性函数和具体函数的研究。本文利用最优控制理论的方法，在文献[11]提出的模型基础上进行研究。通过引入控制变量，提出目标函数，转化为最优控制的问题，并以数值模拟验证其正确性。

1模型

所有计算机分为易感染病毒计算机S，已感染病毒计算机I,获得暂时性免疫计算机R。本文根据文献[11]，提出带有控制的计算机病毒模型如下:

(1)

在文献[11]中,p为免疫率;b为入网率;考虑到杀毒软件的存在，每台易感染病毒计算机S都获得暂时性免疫，此时的免疫率为α1;μ为断网率;γ为暂时性免疫计算机R重新成为易感染病毒计算机的比率;γ2为已感染病毒计算机成为易感染病毒计算的杀毒率;α为已感染病毒计算机获得免疫的免疫率;由于已感染病毒计算机的侵入，t时刻每台易感染病毒计算机S的感染率为βI/f(I)。文献[11]中的字母表示和本文模型中字母具有相同的意义。但是在实际情况中，用户可以通过操作杀毒软件来控制感染病毒的计算机数目，而文献[11]中杀毒率γ2和α是常数，不能很好地反映人为操作杀毒软件的作用。因此，本文在文献[11]的基础上进行改进，将常数γ2和α改成控制变量函数ωu(t)和(1-ω)u(t)，这里u(t)代表杀毒率。根据文献[12]，标准发生率更加符合实际情况，所以本文将一般发生率f(I)改为f(S,I)。

2最优控制问题

根据庞德里亚金的极小值原理，需要在系统 (1)上建立一个最优控制系统来控制病毒的传播。为了建立最优控制系统，对于给定的整数T>0，选择下面的集合作为控制集：

U={u(t)∈L2(0,T):0≤u(t)≤1,0≤t≤T}，

(2)

其中，控制变量u(t)可以通过更新杀毒软件，将感染病毒的计算机数目降低到一个较低水平甚至几乎为0。

目标泛函定义为：

(3)

其中：t0为控制的起始时刻;tf为控制的终点时刻;S11、R11、Q11表示对应变量的权重。给定初始条件为：

S(t0)=S0,I(t0)=I0,R(t0)=R0。

(4)

选取上述的目标函数J(u(t))是为了既能保证将受感染的计算机的数量控制到最低水平，同时也可以保证为此而购买的杀毒软件和软件的更新费用最少。

为了找到目标泛函的最小值，定义Hamiltonian函数[13]如下：

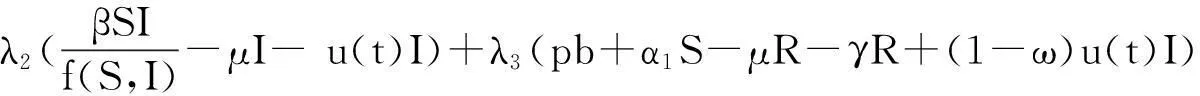
(5)

最优控制的存在性证明。由文献[14]，且方程(1)~方程(3)满足如下条件：

(Ⅰ)控制集和相对应的状态变量集为非空集合。

(Ⅱ)可测集U是闭的凸集。

(Ⅲ)系统(1)方程的右边关于u的线性函数，并且是连续有界的。

(Ⅳ)目标泛函的被积函数L(I,u)在U上是凹函数。

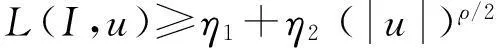
综上所述，系统(1)存在最优控制。

利用庞德里亚金的极小值原理求出最优控制的必要条件如下[13]：

(Ⅱ)斜状态方程：

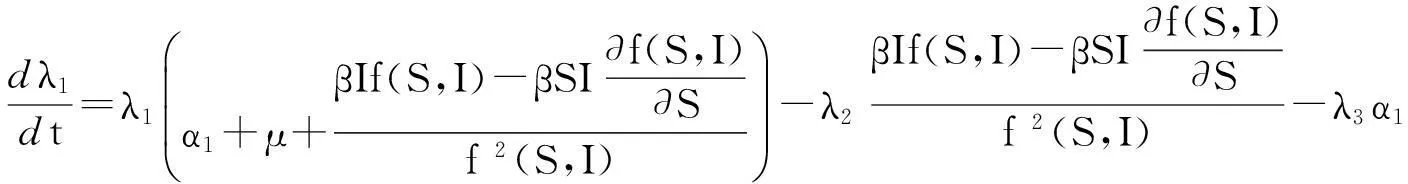
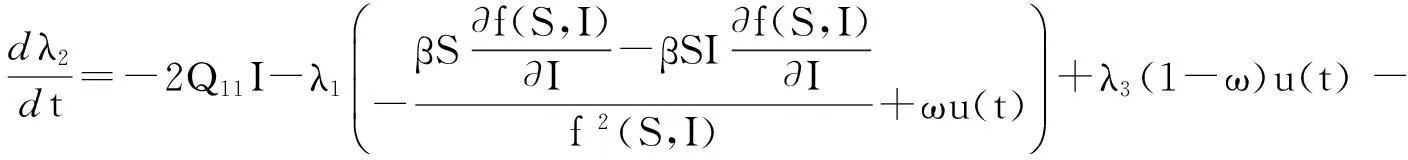
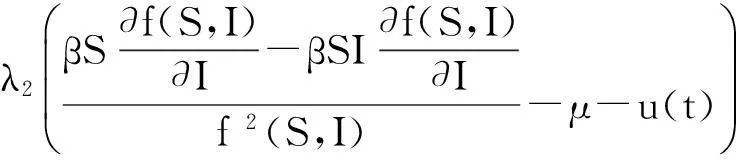
(Ⅲ)横截条件：λi(T)=0，i=1，2，3。

(Ⅳ)边界条件：S(t0)=S0,I(t0)=I0,R(t0)=R0。

因为假定控制的范围是0≤u(t)≤1，本文得到最优控制变量如下：

3数值模拟

根据前面的理论分析，通过数值模拟来验证使用适当的控制策略之后，计算机病毒传播将得到有效控制。此外，将杀毒率分别是常数和变量函数进行比较，通过数值模拟得到：时变的最优控制模型能够更加有效地抑制计算机的感染和病毒的传播。

数值模拟选取如下参数：p=0.1，b=5，α1=0.1，μ=0.003，β=0.038，γ=0.6，γ1=0.01，γ2=0.003，ω=0.5;初值选取：S(0)=800，I(0)=200，R(0)=50。 控制的时间t0=0，tf=100，S11=0，Q11=1 000，R11=5 000。

图1为在有无控制条件下，未感染、易感染和免疫的计算机数量的变化趋势和控制量。

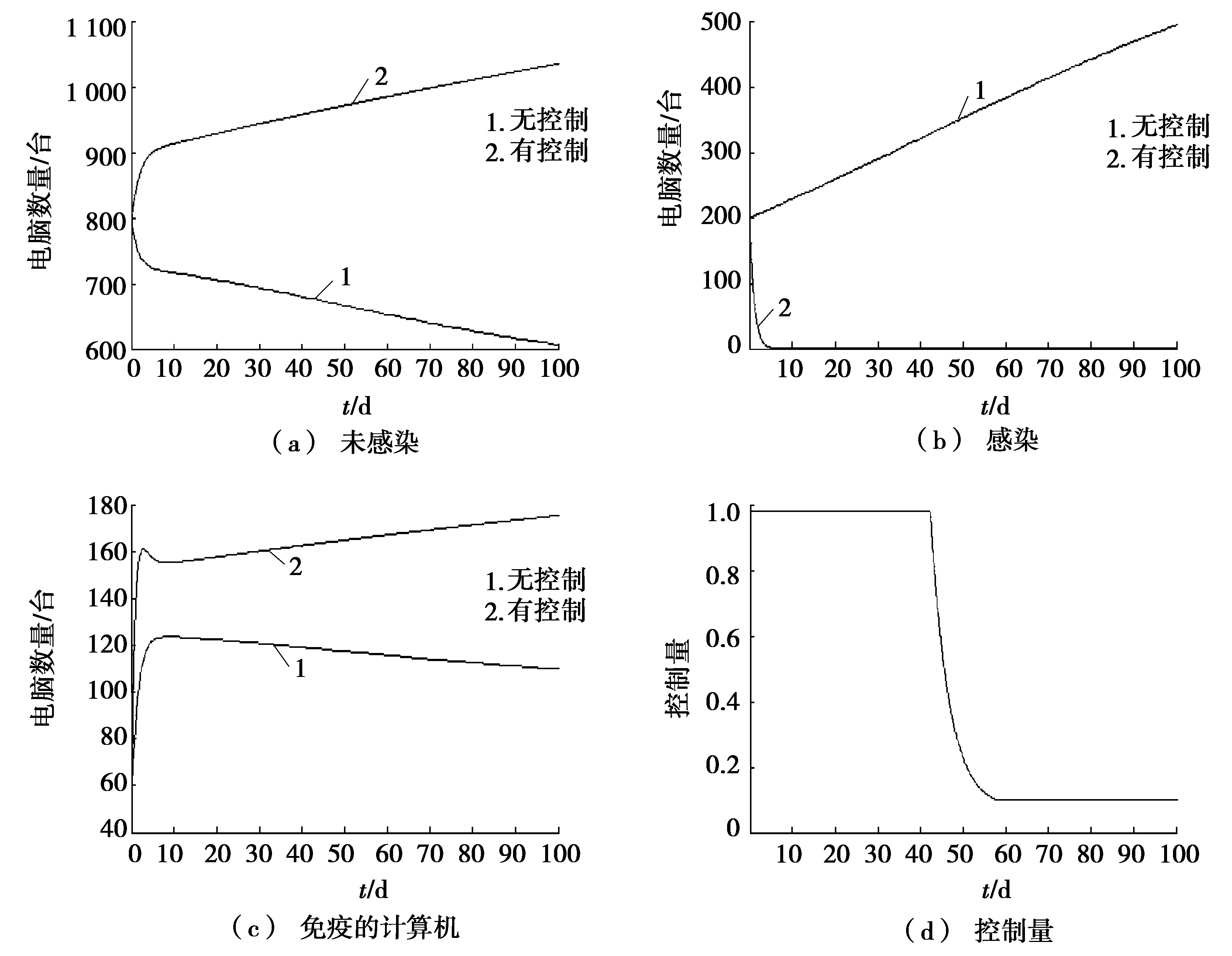
图1　在有无控制条件下，未感染、易感染和免疫的计算机数量的变化趋势以及控制量

由图1可看出：在经过如图1d的控制量的条件下，计算机病毒的蔓延和传播得到了有效的控制。通过图1a可明显看到：在没有有效控制的条件下，易感染的计算机数量是明显下降的，甚至接近600，而在经过控制的条件下，易感染计算机的数量(也就是健康的计算机数量)是逐渐增加的。图1b中显示的是被感染的计算机的数量，同样的，在没有控制的条件下，感染的计算机数量几乎呈直线上升，如果是这样，造成的后果将不可估量。加入了控制，也就是杀毒软件，在前5天被感染的计算机数量就降下来了。同样对于图1c，在加入控制之后的免疫的计算机较以往也是有所提升。图1d表示最优控制量的变化趋势。通过图1d可以看到：在控制的前42天需要保持控制的最大效力，从第42天到第55天，控制逐渐降到极小值;而再从第55天到第100天，控制的效力维持在0.15，也就是说只需维持一个低的效力就能保证计算机都是健康的。

4结论

在有最优控制条件下，易感染的计算机的数量和被感染的计算机的数量趋势是符合目标函数的预期，而在没有控制的条件下，计算机病毒的传播无法被控制。从控制量的走势也可以明显看到：并不需要一直持续的最大效力，就可以将计算机病毒的传播控制住。这也是符合最优控制的目标：在费用最小的前提下，被感染的计算机的数量最少。

参考文献：

[1]Wierman J C,Marchette D J.Modeling Computer Virus Prevalence with a Susceptible Infected Susceptible Model with Reintroduction[J].Computational Statistics & Analysis，2004,45(1):3-23.

[2]Yuan H,Chen G.Network Virus Epidemic Model with the Point to Group Information Propagation[J].Applied Mathematics and Computation,2008,206(1):357-367.

[3]Mishra B K,Saini D K.SEIRS Epidemic Model with Delay for Transmission of Malicious Objects in Computer Network[J].Applied Mathematics and Computation,2007,188(2):1476-1482.

[4]Billings L,Spears W M,Schwartz I B.A Unified Prediction of Computer Virus Spread in Connected Networks[J].Physics Letters A,2002,297(6):261-266.

[5]Piqueira J R C,Navarro B F.Epidemiological Models Applied to Viruses in Computer Networks[J].Joumal of Computer Science,2005(1):31-34.

[6]Gan C Q,Yang X F,Liu W P,et al.A Propagation Model of Computer Virus with Nonlinear Vaccination Probability[J].Commun Nonlinear Sci Numer Simulat,2014,19:92-100.

[7]Mishra B K,Pandey S K.Dynamic Model of Worms with Vertical Transmission in Computer Network[J].Applied Mathematics and Computation,2011,217:8438-8446.

[8]王娟;何俊杰;王倩.一类具有时滞的媒介传染病模型非负解的存在性[J].郑州大学学报:理学版,2014,46(3):1-4.

[9]张旭龙,杨小帆.计算机病毒的最优控制模型[J].计算机应用研究,2011,28(8):3040-3042.

[10]Zhu Q Y,Yang X F,Yang L X,et al.Optimal Control of Computer Virus Under a Delay Model[J].Applied Mathematics and Computation,2012,218:11613-11619.

[11]Gan C Q,Yang X F,Liu W P,et al.An Epidemic Model of Computer Viruses with Vaccination and Generalized Nonlinear Incidence Rate[J].Applied Mathematics and Computation,2013,222:265-274.

[12]Min L Q,Su Y M,Kuang Y.Mathematical Analysis of a Basic Virus Infection Model with Application to HBV Infection[J].Rocky Mountain J Math,2008,38:1573-1584.

[13]秦晓慧,黄健群,董海瑞,等.现代控制理论与应用[M].北京:国防工业出版社,2007:186-191.

[14]Kamien M I,Schwartz N L.Dynamics Optimization:the Calculus of Variations and Optimal Control in Economics and Management[M].Netherland:Elsever Science,2000.