基于模糊Smith方法的航标烤漆室恒温控制系统设计

张 晶 ，吴和宣 ，魏 武

（1.华南理工大学 自动化科学与工程学院，广州 510641；2.广东省航道局，广州 510030）

航标是保障海（江）中船舶安全航行的重要助航设施。一个新投放于海（江）中工作的浮标，随着工作时间的延续，长期浸泡在水中表面易受腐蚀，最终要周期性的回收保养。航标表层防腐蚀涂装的质量对浮标的周期性寿命有着决定性的影响[1]。

防腐涂装的油漆涂上后需要在专用的航标烤漆室进行恒温烘干，烤漆室的温度控制对于航标涂装最后的质量具有较大影响。航标烤漆室作为被控对象具有典型的大滞后大惯性的特点，由于在其中进行烘干的航标数量并不确定，故还具有时变的特点，其控制难度比较大。

目前全国大多数烤漆室的温度控制采用比较成熟的PID控制方案，其具有结构简单、鲁棒性好、控制直观等优点。但是对于具有大滞后，时变等特点的对象，一般的PID算法很难对其进行快速有效的控制，并且对对象的适应能力较弱[2]。因此，本文设计了一套基于模糊Smith智能控制算法以及STM32单片机的控制系统，用于控制具有大时滞、大惯性以及时变特性的恒温烤漆室。

1 硬件系统结构

本文设计的温度控制方案的硬件系统主要由STM32控制器、温度传感器、功率控制器、时钟与复位电路、输入键盘以及显示模块组成。其中STM32、时钟电路、输入键盘和LCD显示器集成在一块主控板上，安装于工人操作台。温度传感器安装于烤漆室内部并与主控板相连。加热炉功率控制器接收STM32的设定值并控制加热炉的功率。

本方案采用了型号为STM32F103ZET6的芯片作为控制系统的主控制器。该型号芯片自带512 KB的Flash和64 B的SRAM，不需要外接存储器，还拥有3个12位模数转换器ADC、11个定时器、112个快速I/O接口，资源丰富，可以满足本方案的需求，同时保证了较低的成本和功耗[3]。

温度传感器模块采用DS18B20，该模块成本低廉，抗干扰能力强，有12位精度。BS12B20安装于烤漆室内部，通过线路与主控板相连接。测得的温度经STM32的ADC转换为数字量输入，经过模糊Smith控制器算法模块计算后输出PWM波作为加热炉功率控制器的控制信号。

LCD显示模块采用常见的2.8寸TFT-LCD显示屏，用于显示当前温度，加热时间，以及设定温度等数据。另外配有常见矩阵键盘进行系统设置。

功率控制器作为控制单元，接收PWM波，按照PWM波的占空比调整加热炉的功率，以改变烤漆室的温度。硬件系统框图如图1所示。

图1 硬件系统Fig.1 System framework for hardware

2 模糊Smith控制器

2.1 Smith预估理论

时间滞后大系统难以控制的根源是因为控制对象的纯滞后环节会包含在系统的特征方程中，使得系统不稳定。对于时间滞后大的系统，常采用在控制器上并联一个Smith预估器的方法来用于补偿控制对象的纯滞后，消除时滞环节的影响[4-6]。Smith预估的原理框图如图2所示。

图2 Smith预估原理Fig.2 Smith predictor schematic diagram

图中：D（s）为控制器；Go（s）e-τs为带有纯滞后环节的控制对象；Gm（s）（1-e-τms）为 Smith 预估器。 Smith 预估器的 Gm（s）应当尽可能等于被控对象的 Go（s），τm应该尽可能等于被控对象的τ。经过计算可知整个系统的闭环传递函数为

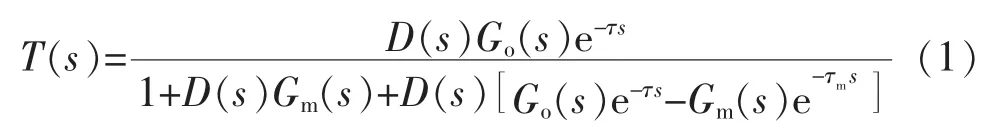
可以看出，能准确得知被控对象的情况下，加入Smith预估控制器可以有效地消除系统传递函数特征方程中的纯滞后环节，使得系统控制效果变得更好。

2.2 模糊PID与Smith预估复合控制器设计

Smith预估需要被控对象的参数来设定控制器，对于大滞后系统，当能够较为准确地获得被控对象的参数的时候，Smith预估控制器的控制效果明显优于常规PID控制。但是在实际生产过程中，往往难以准确获取被控对象的准确模型，如果控制对象的模型误差较大的话控制效果会急剧下降甚至出现发散。考虑到这一情况，本文在控制系统中引入了对模型参数变化不敏感的模糊控制器。

模糊控制器不依赖具体的数学模型，其控制规则库和隶属度函数从成熟的经验中归纳得出。具有动态特性好、抗干扰能力强、对于对象适应性好等优点，目前已有较多学者研究了其在温度控制中的应用[7-9]。同时，针对模糊控制调节精度不高、静差大的缺点，再引入成熟的PID控制器以及Smith预估器组成复合控制器[10-11]。其结构如图3所示。

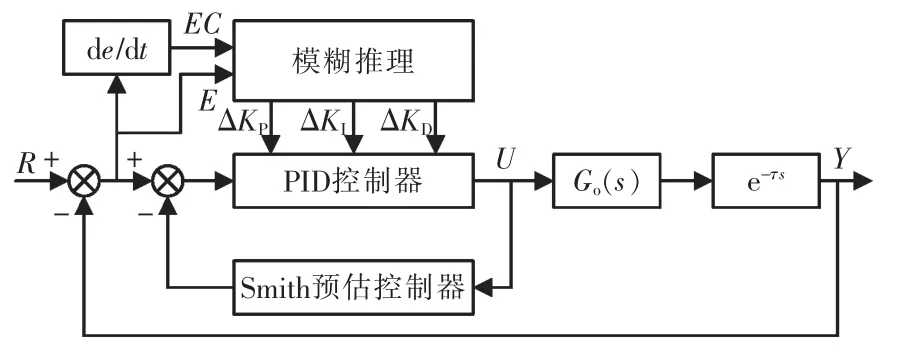
图3 模糊Smith控制器结构Fig.3 Fuzzy Smith controller structure diagram

模糊控制器接收偏差以及偏差的变化率作为输出，通过模糊推理在线调整PID控制器的控制参数。PID控制器两端并联了一个Smith预估器，如前文所述，Smith预估器与控制对象的纯滞后环节相抵消，使得纯滞后环节对特征方程中的极点位置影响减小。Smith预估器的参数与控制对象的实际值误差越小则其控制效果越好。由于模糊控制器对参数误差不敏感，一定程度上可以起到降低模型参数误差干扰的作用。

2.3 参数整定以及模糊推理

在模糊控制器中所有的语言变量的语言值分为 7 个值｛NB，NM，NS，ZO，PS，PM，PB｝，语言值的隶属度函数除NB和PB选用高斯函数以外，其余均选用三角函数。为了增强系统的鲁棒性，隶属度函数在0的附近取得更抖[12]，模糊推理采用典型Mandami型，解模糊方法采用中心法。模糊控制器的隶属度函数如图4所示。

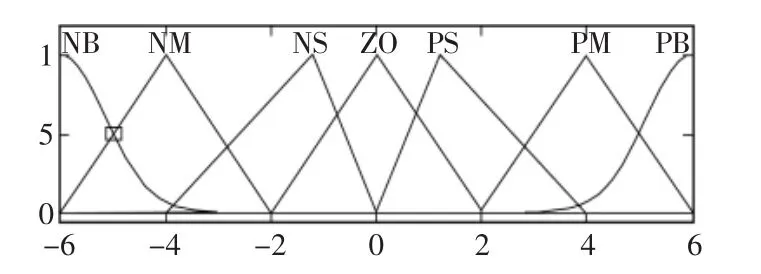
图4 模糊控制器的隶属度函数Fig.4 Membership function of fuzzy controller

模糊控制器的输入为偏差E与偏差的变化率EC，输出为 ΔKP（k）、ΔKI（k）、ΔKD（k）。模糊控制器的输出量对 PID控制器的参数KP、KI、KD进行在线调整，调整公式为

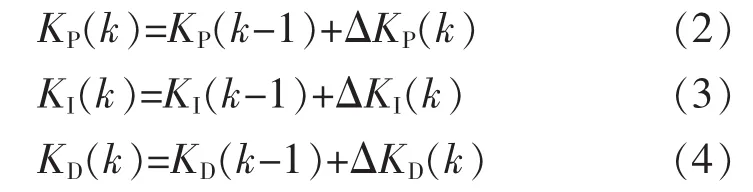
式中：KP（k）、KI（k）、KD（k）为 PID 控制器的比例系数、积分系数、微分系数；ΔKP（k）、ΔKI（k）、ΔKD（k）为PID控制器各个系数的修正量，通过模糊控制器将输入的精确量偏差和偏差变化率进行模糊化、模糊推理以及解模糊等步骤得到，表达式为

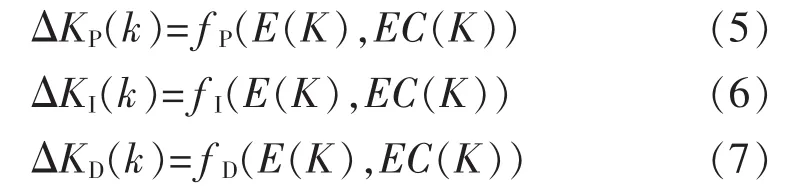
经过人工经验的整定和实验调整，可以取如表1～表3所示的规则库。

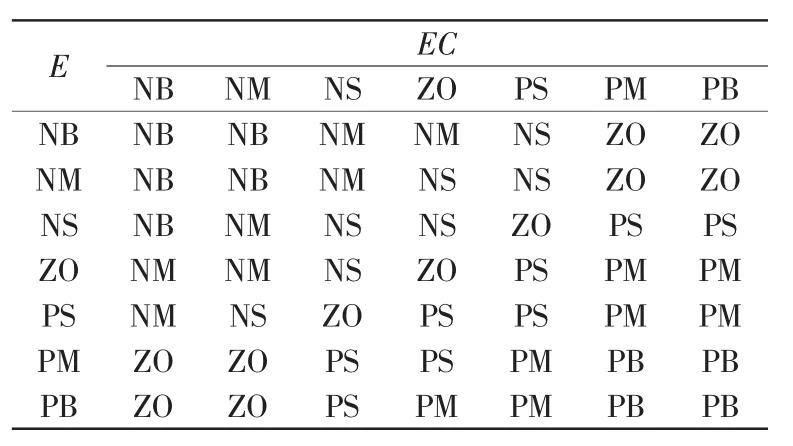
表1 ΔKP的模糊规则Tab.1 Fuzzy rules for ΔKP

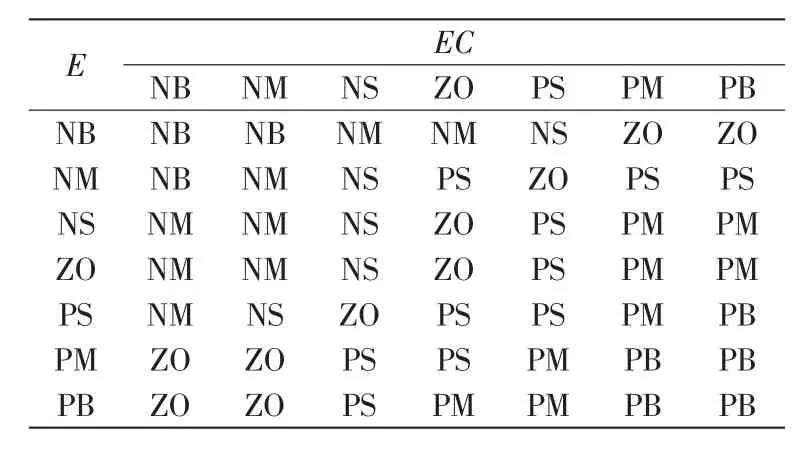
表2 ΔKI的模糊规则Tab.2 Fuzzy rules for ΔKI

表3 ΔKD的模糊规则Tab.3 Fuzzy rules for ΔKD

3 软件结构

在编程实现中，软件主要分为控制器模块、信号转换计算模块、参数配置与显示模块3个部分。控制器模块分为模糊控制模块、PID控制模块、以及Smith预估器3个子部分。3个模块在单片机内部相互通信，整合为整个智能控制器。信号转换模块一方面通过ADC采集的温度数据转换为具有具体物理意义的温度数值，另一方面将控制器的数字输出量转换为相应的PWM波的占空比。参数配置与显示模块用于检测键盘输入、设置跟踪温度与烤漆加热时间等参数，以及在LCD显示屏幕上显示当前系统信息。

开始运行后，系统先获取设定温度，然后采集当前温度，计算偏差和偏差变化率。偏差和偏差变化率输入智能控制器计算输出量，再转化为对应的PWM波控制烤漆室加热器的功率。软件结构框图如图5所示，整体工作流程如图6所示。

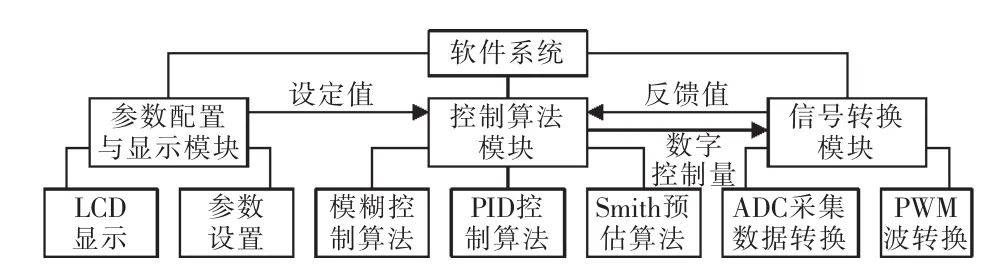
图5 软件结构Fig.5 System framework for software

图6 软件流程Fig.6 Software flow chart

4 仿真与分析

针对前文提出的模糊Smith智能控制方法，采用Matlab/Simulink进行建模以及仿真分析，通过仿真实验对比其与传统PID控制的性能。

首先选定被控对象，一般的大滞后大惯性环节可以近似为1个一阶惯性环节与1个纯滞后环节串联，烤漆室的近似数学模型为

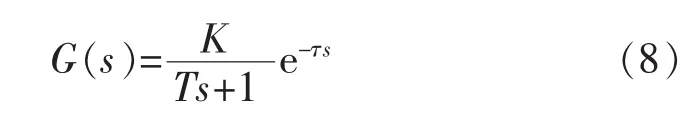
式中：K为增益；T为时间常数；τ为纯滞后时间。对于具体的对象，工程上一般使用实验法来测定被控对象数学模型中的各个参数，常用阶跃响应曲线法、矩形脉冲扰动法、周期扰动法等方法以确定K、T、τ。本文仿真所采用对象 K=2.2，T=2670，τ=130。

实际上由于在设计Smith预估器的时候很难取得准确的对象模型，这里人为设定一定的误差，Smith预估器取为

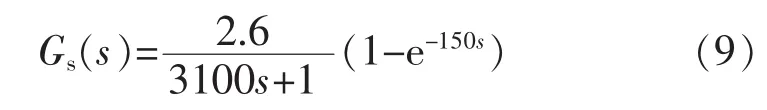
上式在取值的时候人为地按照比被控对象的模型参数T、τ较大的值设定。因为在实际生产过程中，会向烤漆室中加入不定数量的大质量航标，会明显提高被控对象的时间常数以及纯滞后时间，所以在设计Smith预估器的时候，应当将Smith预估器模型中对应的参数对应的时间常数和纯滞后时间适当的取较大的值。确定被控对象和Smith预估器的参数后，在Simulink中搭建仿真模型进行仿真。

4.1 与常规控制方案的对比

对于前文所述的控制对象，分别采用模糊Smith控制与PID控制经过调整整定控制参数和各个系数后，进行仿真分析，可以得到如图7所示的响应曲线。曲线A为模糊Smith控制器的响应曲线，曲线B为经过参数整定后的常规PID控制器的响应曲线。

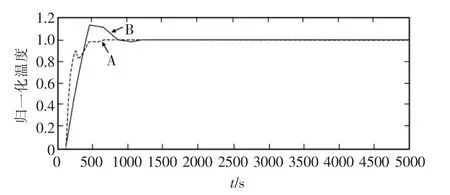
图7 两种控制方案的阶跃响应Fig.7 Step response of two kinds of methods

当取Δ=0.05时，2种方案的控制效果如表4所示。

表4 阶跃响应控制效果Tab.4 Controll effect of step response

在保证基本无静差的条件下，采用模糊Smith智能控制器对大滞后大惯性对象进行控制具有响应快、超调小的特点，其控制效果明显优于常规PID控制。

4.2 抗扰动能力

保持控制参数不作改变，在t=3000 s时在控制对象前面加入一个幅值为0.3的阶跃扰动信号，响应曲线如图8所示。A为模糊Smith控制器的响应曲线，B为PID控制器的响应曲线。A曲线由于阶跃干扰造成的偏离小于B曲线，模糊Smith控制器的抗干扰能力比常规PID控制器有一定提升。

图8 两种控制方案的抗扰动性能Fig.8 Comparison of the ability of anti-disturbance between two controll method

4.3 对控制对象改变的适应性

如前文所述，加入烤漆室烘烤的航标会使得整个被控对象的时间常数和纯滞后时间出现较大增加。因此，这里将被控对象进行修改，时间常数T由2670增加到4500，纯滞后时间τ由130增加到200。在保持控制器的各个参数完全不变的情况下进行仿真，得到如图9所示的响应曲线。曲线A为模糊Smith控制器的响应曲线，曲线B为PID控制器的响应曲线。

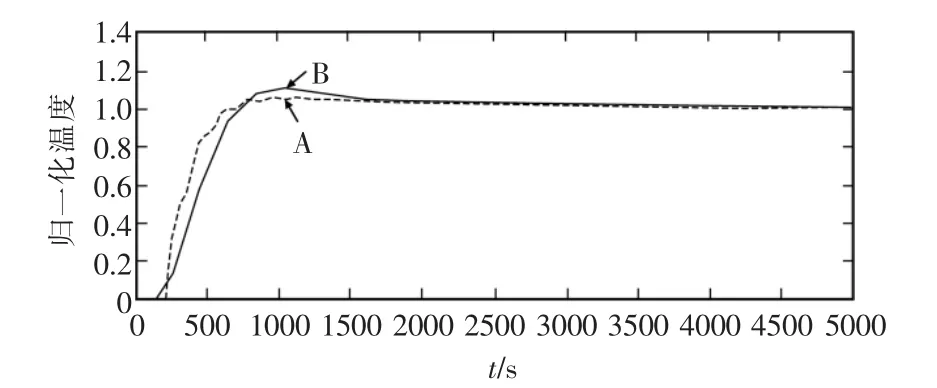
图9 被控对象变化时的响应曲线Fig.9 Correspondence curv when the controlled object been changed

当取Δ=0.05的情况下，控制效果如表5所示。

表5 被控对象变化时的控制效果Tab.5 Controll effect when the controlled object been changed

在控制器不做任何更改，而烤漆室加入大量航标导致被控对象的惯性和纯滞后大幅度增加的情况下，模糊Smith控制器体现出了明显的优势，响应速度降低的程度远低于PID控制器，并且超调量更小。

5 结语

本文针对航标烤漆室控制对象大滞后、大惯性、时变的特点，设计了一套基于STM32单片机模糊Smith恒温控制系统，硬件成本低廉、实现方便。经过仿真实验表明，对于大时滞大惯性的烤漆室控制对象，采用模糊Smith智能控制方法与常规PID控制器相比具有响应速度快、超调小、抗干扰能力强的特点，而且对于被控对象的参数变化不敏感，在模型参数不准确并且时变的条件下明显具有更好的适应能力。

[1]李石莲，陈宇红，李明佳.海上航标重防腐方法应用[C]//中国航海学会航标专业委员会沿海航标学组、无线电导航学组、内河航标学组年会暨学术交流会，2009.

[2]李科.温控系统的智能PID控制算法研究[D].湖北：华中科技大学，2006.

[3]廖义奎.Cortex-M3之STM32嵌入式系统设计[M].北京：中国电力出版社，2012.

[4]朱晓东，王军，万红.基于Smith预估的纯滞后系统的控制[J].郑州大学学报：工学版，2004，25（1）：77-81.

[5]赵东亚，邹涛，王治平.Smith预估控制研究进展[J].化工进展，2010，29（8）：1406-1410.

[6]杜锋.基于新型Smith预估器的网络控制系统研究[D].成都：西南交通大学，2008.

[7]李丹，谢植，程杰.模糊控制在温度控制系统中的应用与发展[J].黄金学报，2000（4）：294-297.

[8]路桂明.基于模糊PID控制的电锅炉温度控制系统的研究[D].哈尔滨：哈尔滨理工大学，2007.

[9]段江霞.模糊PID控制在大惯量时滞温度控制系统中的应用研究[D].兰州：兰州大学，2013.

[10]杨凯锋.模糊Smith智能控制方法的研究及其单片机实现[D].湖南：湖南大学，2005.

[11]崔颖.基于Smith预估器的模糊PID控制方法研究[D].大连：大连理工大学，2006.

[12]文定都，何玲.基于Smith模糊PID控制算法的炉温控制系统[J].仪表技术与传感器，2009（4）：107-108.