基于PSO优化BP神经网络的逆运动学求解研究

赵建强 ，刘满禄 ，2，王 姮

（1.西南科技大学 特殊环境机器人技术四川省重点实验室，绵阳 621010；2.中国科学技术大学 信息科学技术学院，合肥 230026）

机器人的运动学逆解问题是对智能机器人进行运动规划与智能控制的重要前提。其本质就是通过给定的机器人末端位姿参数来求取对应位姿的机器人各个关节变量的值。自机器人学创立以来，该问题一直是机器人领域的研究热点[1]。运动学逆解的传统求解方法主要有几何法[2]、解析法[3-4]、迭代法[5]等。可以通过解析法得到简单机构的封闭解，复杂机构一般很难得到封闭解，需要进行迭代处理，然而迭代法的运算量很大、精度无法保证、耗时较长导致了实时性比较差，几何法对机构的构型要求比较严格，通用性受到了很大的限制。机械臂的实时控制对于机械臂的应用是至关重要的，这其中一个关键的影响因素就是逆运动学求解的快速性。训练完毕的神经网络，其运算速度非常快，故而越来越多的研究者关注于用神经网络来解决机械臂的逆运动学求解问题[6-8]。针对传统的BP神经网络存在收敛速度慢、易陷入局部极值导致输出误差偏大的缺陷，已经提出了一些用来优化BP神经网络的方法，主要从优化神经网络结构[9]、优化网络中的权值和阈值[10-11]、更改神经网络的训练样本组织形式[12]以及对网络输出结果的优化[13]。本文利用PSO对BP神经网络进行优化，在随机初始化BP神经网络的权值和阈值之后，通过适应度函数计算PSO粒子的适应度，根据粒子自身的历史最优和全局最优来更新粒子的位置和速度，从而不断地搜索最优的方向，在加快收敛速度的同时，逐渐向全局最优收敛，将优化后的BP神经网络应用到机器人逆运动学的求解问题上。结合MotomanMH6S机械臂做了运动学仿真实验，验证了其在机器人逆运动学求解应用中的有效性。

1 BP神经网络及逆运动学分析

1.1 MotomanMH6S的运动学分析

根据文献[14]对MotomanMH6S机器人进行运动学建模。首先在机器人的每个连杆上都固定一个坐标系，得到如图1所示的机器人连杆坐标模型，用 ai、αi、di、θi4 个运动学参数描述机器人的每个连杆，得到其D-H参数，如表1所示。

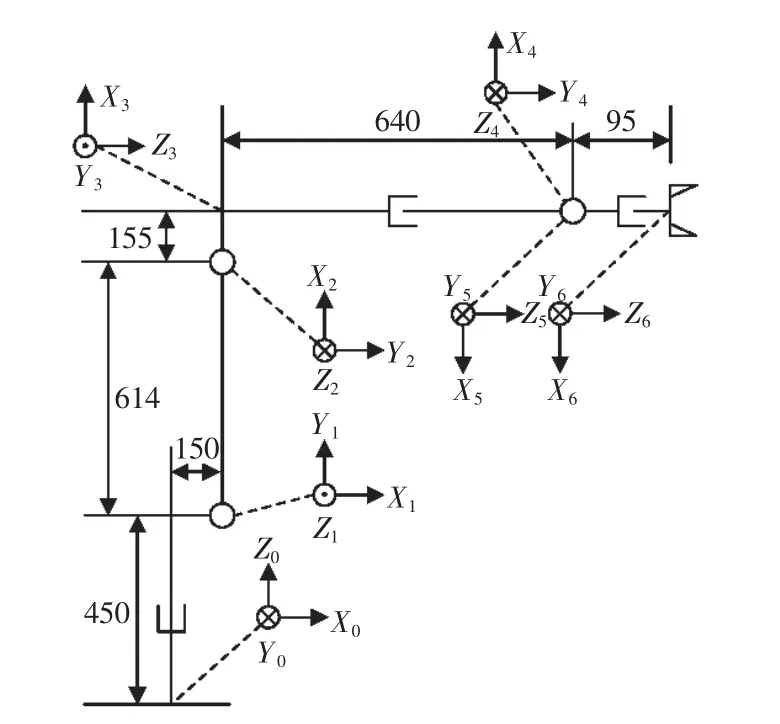
图1 Motoman MH6S机器人连杆坐标模型Fig.1 Robot Motoman MH6S linkage coordinate model diagram

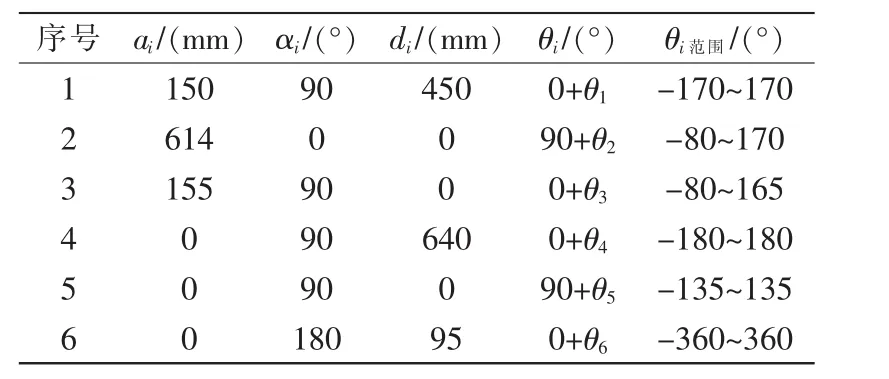
表1 MotomanMH6S的D-H参数Tab.1 Motoman MH6S D-H parameter

根据表1所示的Motoman MH6S机器人的D-H参数，可计算机械臂各相邻连杆的位姿变换矩阵为

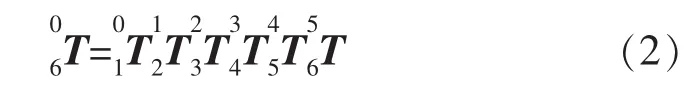
则其运动学方程为

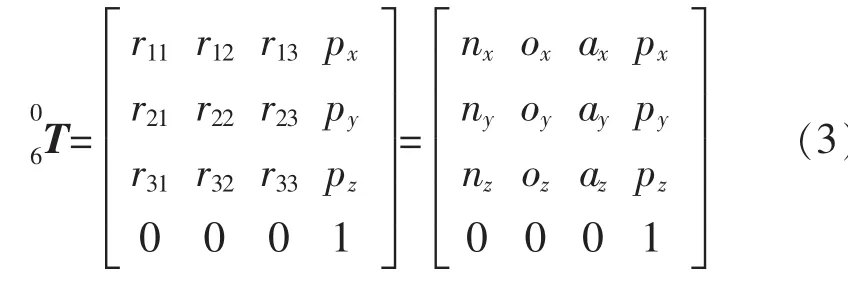
已知机器人各个关节的关节变量θi（i=1，2，…，6），根据式（2）、式（3）可求出末端执行器的姿态 R（nx，ny，nz，ox，oy，oz，ax，ay，az）和位置 P（px，py，pz），这就是机器人的运动学正解，可通过运动学正解来得到机器人操作空间数据集。由给定操作空间的姿态（nx，ny，nz，ox，oy，oz，ax，ay，az）和 位 置 （px，py，pz）来 求 解关节空间机器人的关节变量 θi（i=1，2，…，6）的过程就是逆运动学。由于nx，ny，nz是机器人末端执行器所在坐标系的OX轴相对于基坐标系的3个方向余弦，ox，oy，oz是机器人末端执行器所在坐标系的OY轴相对于基坐标系的3个方向余弦，ax，ay，az是机器人末端执行器所在坐标系的OZ轴相对于基坐标系的3个方向余弦，可根据坐标变换原理，将姿态R按Z-Y-Z轴的旋转序列进行欧拉变换得到欧拉角α、β、γ，变换公式为

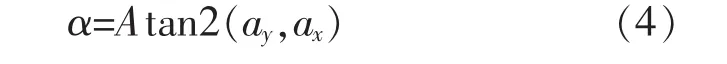
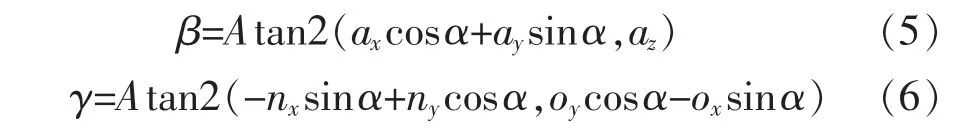
式中，Atan2 为反正切函数。 将 α、β、γ、px、py、pz作为BP神经网络模型的输入变量，关节变量θi（i=1，2，…，6）为模型的输出变量。

1.2 BP神经网络

BP网络可以比作是从输入到输出的高度非线性映射，即F∶Rn→Rm，其最大特点是通过误差的反向传播来修正网络的权值和阈值，本质是从输入Xi∈Rn到输出 Yi∈Rm可存在某一映射 Γ（·），使yi=Γ（xi）（i=1，2，…，n），要求出映射 F（·），使得在某种意义下（通常在最小二乘意义下），F（·）是 Γ（·）的最佳逼近，神经网络对简单的非线性函数进行数次逼近复合，可近似表达复杂的函数，这种任意逼近的存在性问题可由Kommogorow定理及通用逼近定理给出。其中单个神经元为McCulloch-Pitts模型[15]，如图2所示。

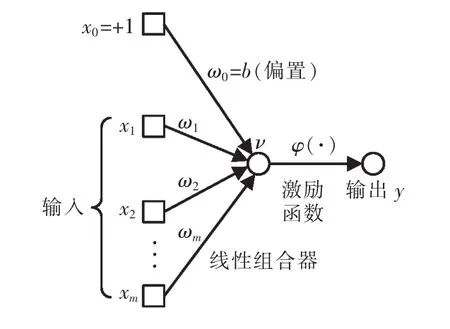
图2 单个神经元的McCulloch-Pitts模型Fig.2 McCulloch-Pitts model of individual neurons

图中输入向量的分量为 xj（j=1，2，…，m），输入的权值分量为 ωj（j=1，2，…，m）。若权值为正数，则表示相应的输入节点处于兴奋状态，起加强作用；若权值为负数，则起抑制作用。φ（·）为激励函数，其输入ν是输入向量的加权之和，称为诱导局部域。理论上已经证明，隐含层采用sigmoid型激励函数的3层前馈神经网络可以以任意精度逼近任何连续映射。在本文的网络结构中，输入层有6个神经元，分别对应 α、β、γ、px、py、pz；输出层有 6 个神经元，分别对应6个关节的关节角。隐藏层神经元个数的选择是一个很复杂的问题，目前还没有任何一个理论指导精确地计算隐藏层神经元个数，只能通过经验和多次实验来确定。若隐藏层神经元太少，不能满足系统对训练精度的要求，若隐藏层神经元太多，会导致网络的训练时间过长且泛化能力减弱。在对各种结构进行大量试验、比较之后，选取2个隐含层，节点数分别为21和29。本文设计的BP神经网络拓扑结构如图3所示。

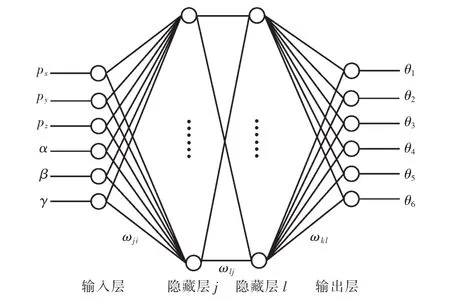
图3 BP神经网络拓扑结构Fig.3 BP neural network topology structure

2 基于PSO优化的BP神经网络

粒子群优化算法（PSO）起源于对鸟群捕食的行为研究，是一种基于进化的计算技术。系统初始化为一组随机粒子，粒子在解空间追随最优的粒子进行搜索，通过迭代搜寻最优值，所以PSO是一种基于迭代的优化工具。在每一次迭代中，粒子通过跟踪2个“极值”来更新自己。第一个就是粒子本身所找到的最优解。这个解叫做个体极值Personal Best.另一个极值是整个种群目前找到的最优解。这个极值是全局极值Global Best。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居，那么在所有邻居中的极值就是局部极值。

假设在D维空间中存在m个粒子，将第i个粒子的速度向量记为 Vi=［vi1，vi2，…，viD］，将其位置向量记为 Xi=［xi1，xi2，…，xiD］，在每一次迭代中，粒子根据2个因素更新自己的速度和位置，一个是该粒子自身的历史最优值，记为 Pi=［ pi1， pi2，…， piD］，另一个是整个粒子群体的全局最优值，记为G=［g1，g2，…，gD］，其速度和位置的更新公式为[16]

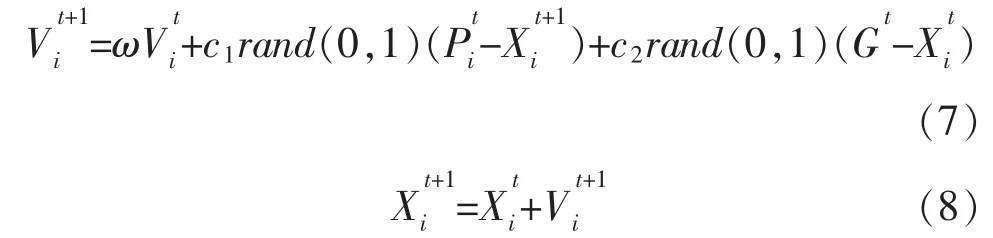
式中：rand（）是（0，1）之间的随机数；ω 是粒子保持原来速度的系数，即惯性权重；c1是粒子追踪其历史最优值的随机加速度项权重，代表粒子的自身经验；c2是粒子追踪全局最优值的随机加速度项权重，代表粒子的社会经验；t为当前迭代次数。为防止粒子的盲目搜索，一般建议将其位置和速度限制在一定的区间［-Xmax，Xmax］、［-Vmax，Vmax］[17]。

单纯的BP神经网络算法在求解逆运动学的时候存在易陷入局部极值、输出误差偏大、学习效率不高等问题。为了解决上述问题，本文运用PSO算法优化BP神经网络参数，使得搜索在整个解空间中进行，通过优化得到的最佳网络参数改善了BP神经网络的网络结构，从而提高了BP神经网络的泛化能力。算法流程如图4所示。

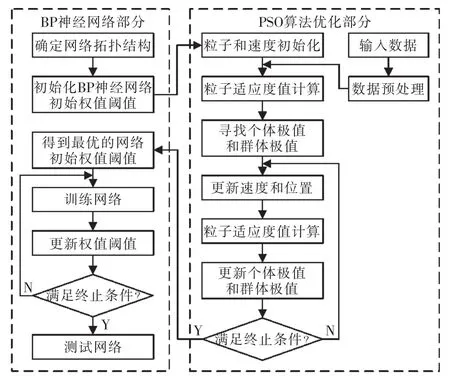
图4 PSO优化BP神经网络算法流程Fig.4 Algorithm flow chart of PSO optimize the BP neural network

将采样数据进行归一化处理，确定BP神经网络结构并且随机生成初始权值、阈值，将初始的BP神经网络参数作为粒子初始值，计算相应粒子的适应度，然后通过迭代找到最优解。其中，适应度函数定义为BP神经网络训练时输出的关节角度与期望关节角度误差的平方和，表示为

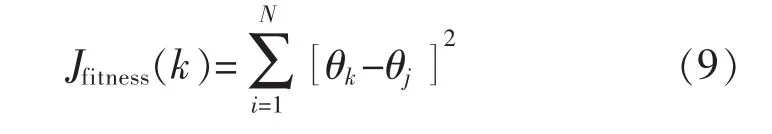
其中，网络的输出θk是关于网络权值ω的函数：

同时设置其他参数如下：种群规模定为30，最大代数为50，惯性权重ω=0.9，学习因子c1=c2=1.5，BP神经网络隐层的神经元个数为21、29，输入层到隐层与隐层到隐层之间的传递函数为sigmoid，隐层到输出层的传递函数为linear，为了提高训练速度，训练算法选用Levenberg-Marquardt反向传播方法。对优化后的BP神经网络进行训练，并对最终训练得到的神经网络进行测试。

3 优化算法在逆运动学中的求解

网络结构和PSO的参数确定以后，将使用样本数据对算法进行训练。在仿真实验中，采用Motoman-MH6S型机器人在其工作空间的10000组数据，其中选用9500组数据用作训练样本，500组数据用作测试样本。首先将训练样本中的位置向量和姿态欧拉角作为BP神经网络的输入节点，关节角度作为网络的输出节点，然后采用PSO算法以式（9）作为适应度函数在解空间进行优化搜索。粒子群收敛以后，返回BP神经网络的权值和阈值。对优化并训练好的网络，用测试样本数据进行仿真测试，求得网络对样本中各个关节角变量的输出值。

网络训练后，对于训练样本，网络性能（MSE）为0.060379。将测试样本中的500组关节角度期望值与PSO优化的BP神经网络求出的关节角度进行比较得到其误差范围为［-0.0906，0.0848］，测试集通过该神经网络的输出值的均方差范围为［3.1180×10-5，0.0034］，而未加PSO优化的BP神经网络对500组测试样本求解的误差范围为［-0.4068，0.3536］，均方差范围为［1.5258×10-4，0.0383］。 图 5～图 10 为测试集分别经PSO优化的BP神经网络与未加优化的BP 神经网络的输出误差 Δθi/（°）（i=1，2，…，6）的对比，图11为测试集经上述2个神经网络输出的MSE对比，表2、表3为测试集的误差，均方差表现范围。

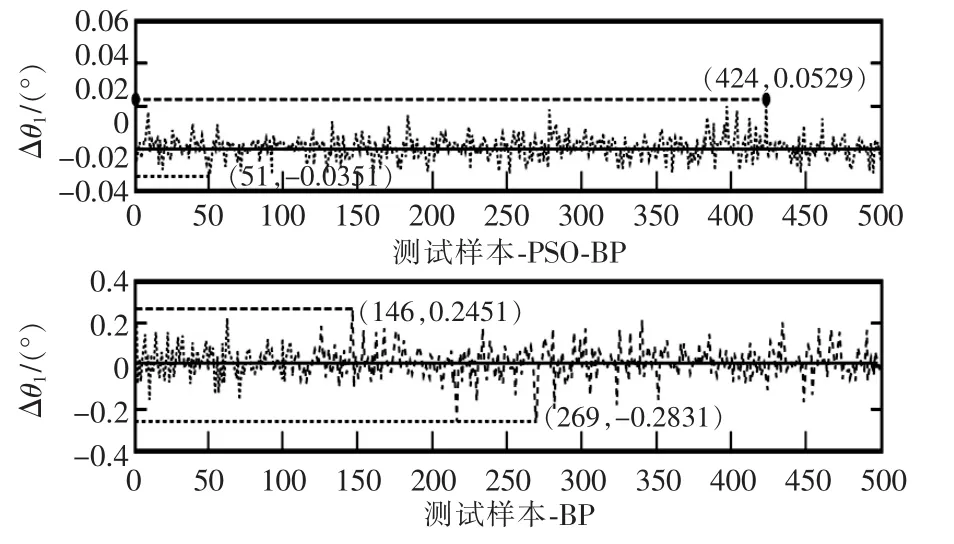
图5 测试集的θ1的误差对比Fig.5 Error contrast of the test set’s θ1

图6 测试集的θ2的误差对比Fig.6 Error contrast of the test set’s θ2

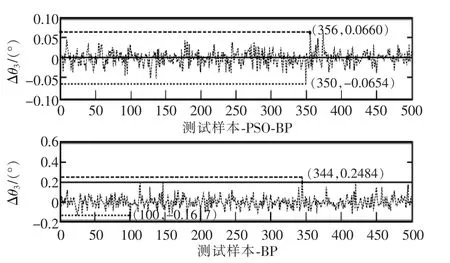
图7 测试集的θ3的误差对比Fig.7 Error contrast of the test set’s θ3

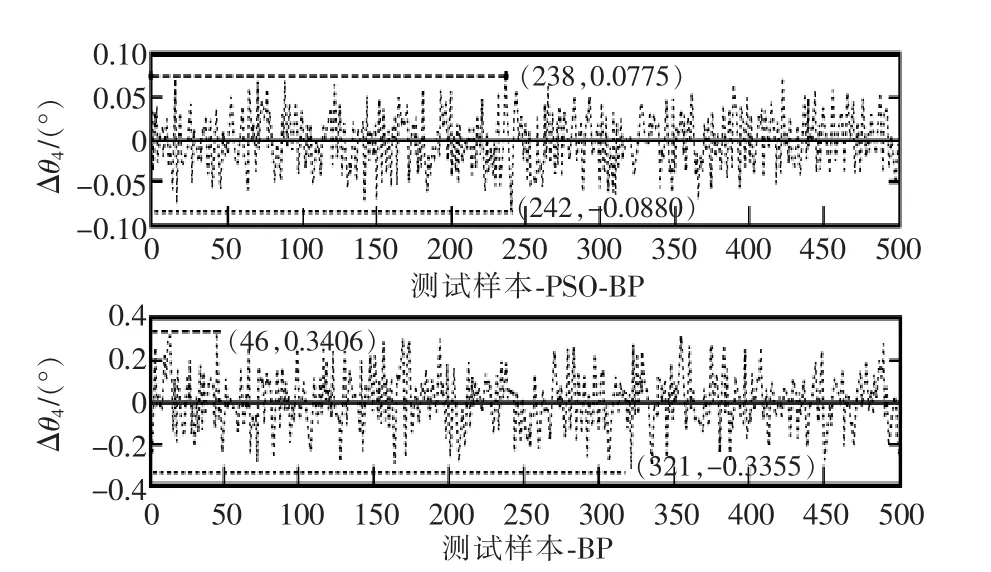
图8 测试集的θ4的误差对比Fig.8 Error contrast of the test set’s θ4

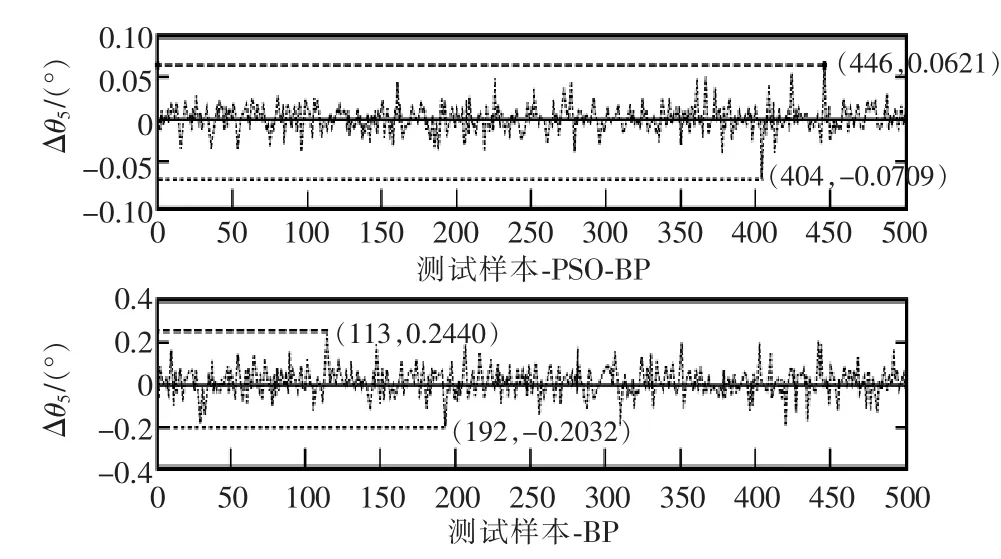
图9 测试集的θ5的误差对比Fig.9 Error contrast of the test set’s θ5

图10 测试集的θ6的误差对比Fig.10 Error contrast of the test set’s θ6

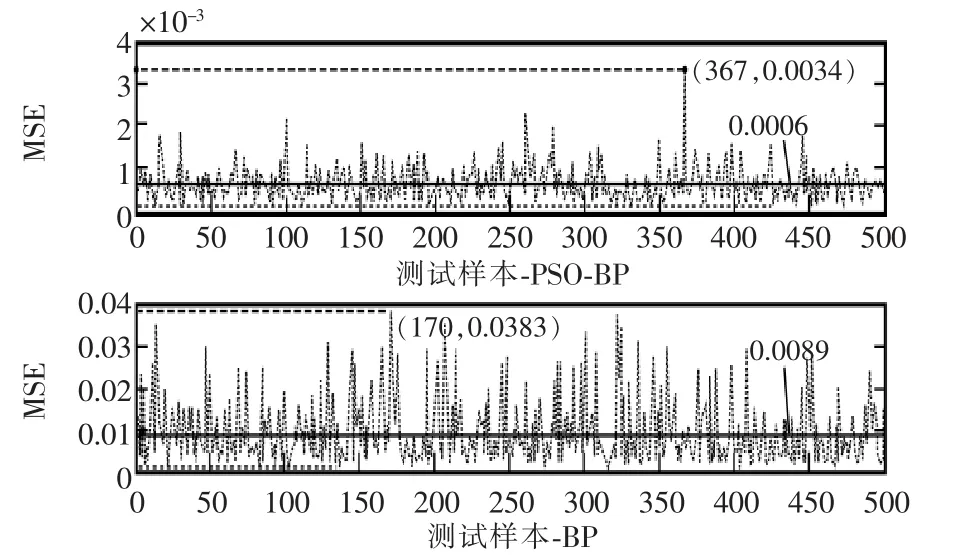
图11 测试集的θ的MSE对比Fig.11 MSE contrast of the test set’s θ

表2 测试集θi的误差表现范围Tab.2 Error range of test set’s θi

表3 测试集θ的均方差表现范围Tab.3 MSE range of test set’s θ

由图5～图10可得知，PSO优化的BP神经网络在求解机械臂逆运动学时的误差表现明显比单纯的BP神经网络提高了一个数量级。由图11可知，PSO优化的BP神经网络在求解机械臂逆运动学时的均方误差表现也比单纯的BP神经网络提高了一个数量级。同时，表2中可得知PSO优化的BP神经网络在求解机械臂逆运动学时的最大误差在［-0.1，0.1］之间，这进一步验证了本文方法在机械臂逆运动学求解方面的有效性。

文献[6]中最终选择的最优BP神经网络对四自由度机械臂的逆运动学求解所得的关节角度误差表现范围与本文中PSO-BP对六自由度机械臂的逆运动学求解所得的关节角度误差表现范围对比如表4所示，其中将文献[6]中的单位由弧度值转换为角度值表示。由表4中数据的对比可得出PSO-BP在求解机械臂逆运动学时的关节角度输出精度比文献[6]中的BP神经网络高一个数量级，从而验证了本文提出的PSO-BP在求解机械臂逆运动学应用中的有效性。

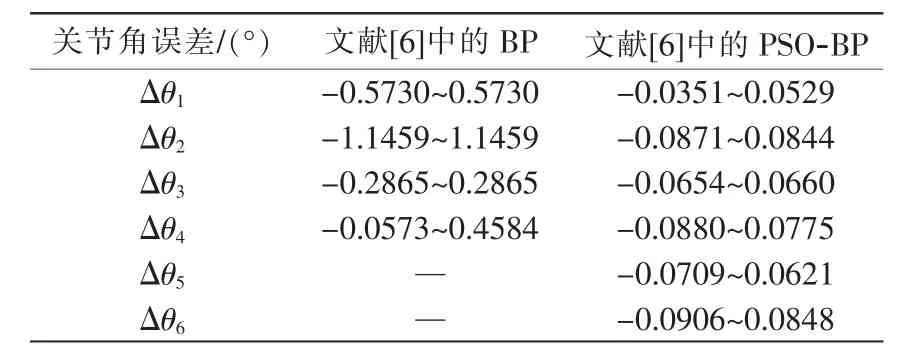
表4 文献[6]中的BP与PSO-BP在求解逆运动学时的误差对比Tab.4 Error contrast of PSO-BP and BP in paper[6]for solving inverse kinematics

4 结语

本文使用PSO优化的BP神经网络来求解机械臂逆运动学问题，得到了比较理想的效果，说明了该方法在机械臂逆运动学求解中的有效性。相比传统的逆运动学求解方法，通过训练BP神经网络来得到从机械臂工作空间到关节空间的复杂非线性映射关系，避免了求解逆运动学时极其复杂的推导过程。但是，单纯的BP神经网络在求解逆运动学时，易陷入局部极值导致输出误差偏大，这直接影响着神经网络在逆运动学求解问题上的实用性，本文通过使用PSO算法对BP神经网络进行优化，弥补了上述缺陷。同时，还有一些问题有待进一步解决，比如由图5和图7可以观察到对于关节角4和关节角6的误差相对偏大，这可能是由于系统中某一特定复杂的耦合关系所致，以及应用神经网络求解机械臂逆运动学时的多解问题和奇异性问题等。接下来可考虑结合RBF、Elman网络及相应的约束条件来寻找这些问题的解决方案。

[1]JohnJ.Craig.机器人学导论[M].贠超，等译.机械工业出版社，2006.

[2]Shimizu M，Kakuya H，Yoon W K，etal.Analyticalinverse kinematic computation for 7-DOF redundant manipulators with joint limits and its application to redundancy resolution[J].IEEE Transactions on Robotics，2008，24（5）：1131-1142.

[3]Vasilyev IA，Lyashin A M.Analyticalsolution to inverse kinematic problem for 6-DOF robot-manipulator[J]，Automation and Remote Control，2010，71（10）：2195-2199.

[4]Loh B G，Rosen J.Kinematic analysis of 7 degress of freedom upper-limb exoskeleton robot with tilted shoulder abduction[J].International Journal of Precision Engineering and Manufacturing，2013，14（1）：69-76.

[5]Korein J U，Badler N I.Techniques for generating the goaldirected motion ofarticulated structures[J].IEEE Computer Graphics and Applications，1982，2（9）：71-81.

[6]李文博，曹兵，张云波.基于BP神经网络的排爆机械臂逆运动学分析[J].计算机测量与控制，2016，24（1）：207-211.

[7]Chen H，Chen W S，Xie T.Wavelet network solution for the inverse kinematics problem in robotic manipulator[J].J Zhejiang Univ.SCIENCE A，2006，7（4）：525-529.

[8]ChiddarwarSS，BabuN R.ComparisonofRBF andMLP neural networks to solve inverse kinematic problem for 6R serial robot by a fusion approach[J].Engineering Applications of Artificial Intelligence，2010（23）：1083-1092.

[9]Oyama E，Agah A，MacDorman K F，et al.A modular neural network architecture for inverse kinematics model learning[J].Neurocomputing，2001，30（40）：797-805.

[10]杨国军，崔平远.机械手逆运动学神经网络算法研究[J].中国机械工程，2002，13（3）：249-251.

[11]LiZ M，LiC G，Lv S J.A method forsolving inverse kinematics ofPUMA560 manipulatorbased on PSO-RBF network[C]//International Conference on Natural Computation，2012：298-301.

[12]郝轶宁，王军政，汪首坤，等.基于神经网络的六自由度摇摆台位置正解[J].北京理工大学学报，2003，23（6）：736-739.

[13]Koker R.A genetic algorithm approach to a neural-networkbased inverse kinematics solution of robotic manipulators based on error minimization[J].Information Sciences，2013（222）：528-543.

[14]Corke P.Robotics，vision and control[M].Berlin：Springer-Verlag，2011：137-139.

[15]HaykinS.神经网络与机器学习[M]申富饶，等译.北京：机械工业出版社，2011.

[16]陈志敏，薄煜明，吴盘龙，等.收敛粒子群全区域自适应粒子滤波算法及其应用[J].南京理工大学学报，2012，36（5）：861-868.

[17]Kinoshita K，Murakami K，Isshiki M.Solution of inverse kinematics by PSO based on split and merge of particles[C]//ICAISC，2013：108-117.