轴用弹性挡圈临界转速计算分析

轴用弹性挡圈临界转速计算分析

李宣秋，张明月，张海平，冯西友

(山推工程机械股份有限公司，山东济宁272073)

摘要：介绍了轴用弹性挡圈使用原理及范围，分析了挡圈临界转速失效机理，建立了单一旋转离心力作用下挡圈受力模型，通过微积分对挡圈模型进行受力分析，给出了在离心力作用下，轴用弹性挡圈临界转速推导方法及计算公式。结合某型号推土机变速箱使用案例，对推导公式进行了验证，为设计及相关问题原因分析提供参考。

关键词:弹性挡圈临界转速危险转速轴用挡圈挡圈模型

中图分类号：TH133.2文献标识码：A

作者简介：李宣秋(1982-)，男，山东济宁人，工程师，硕士，从事工程机械传动系统研究。

收稿日期：2015-04-02

Research on critical rotation speed of elastic collar for shaft

LI Xuanqiu,ZHANG Mingyue,ZHANG Haiping,FENG Xiyou

Abstract:The working principle and application range of axial spring collar is introduced in this paper. The failure mechanism under critical rotational speed is analyzed. The force model of spring collar under single centrifugal force is established, and analyzed with calculus method. Taking this as a foundation, the derivation method and calculation formula of critical rotational speed under single centrifugal force is derived. Taking the actual application of the speed changing box of certain bulldozer as subject, the formula of allowed rotational speed and working principle of axial spring collar is presented, which provides reference for the design of axial spring collar and the analysis of related problems.

Keywords:elastic collar；critical rotation speed；loosen speed；shaft collar；collar model

0引言

在传动系统轴系结构设计中，轴用弹性挡圈由于其安装方便、结构紧凑等优点得到了大量的应用，且其应用范围不断扩展，弹性挡圈的可靠性直接影响着整个传动系统的可靠性及运行安全。[1]

轴用弹性挡圈在工作状态下，如图1所示，随着轴转速的提升，应能依靠挡圈自身弹力及其与挡圈槽底尺寸差卡紧在挡圈槽底随轴一起转动，否则会造成挡圈内圈与挡圈槽底相对运动，造成相关零部件损坏失效，甚至导致挡圈脱落失效。目前对于轴用弹性挡圈的设计，主要依据被固定件相关尺寸，依靠经验或参照已有产品进行设计、选型，这种设计方法对于低速工况基本没有问题，但对于转速逐步提高的现代机械来说，随着轴转速的提升，弹性挡圈在离心力作用下脱离挡圈槽的机率逐步提升，参照设计已经无法满足使用要求[2-3]。文献[2]利用卡氏定理，分析了轴用弹性挡圈的径向变形，为相关设计提供了参考，文献[4]推荐了轴用弹性挡圈许用转速计算公式，但未给出推导过程。

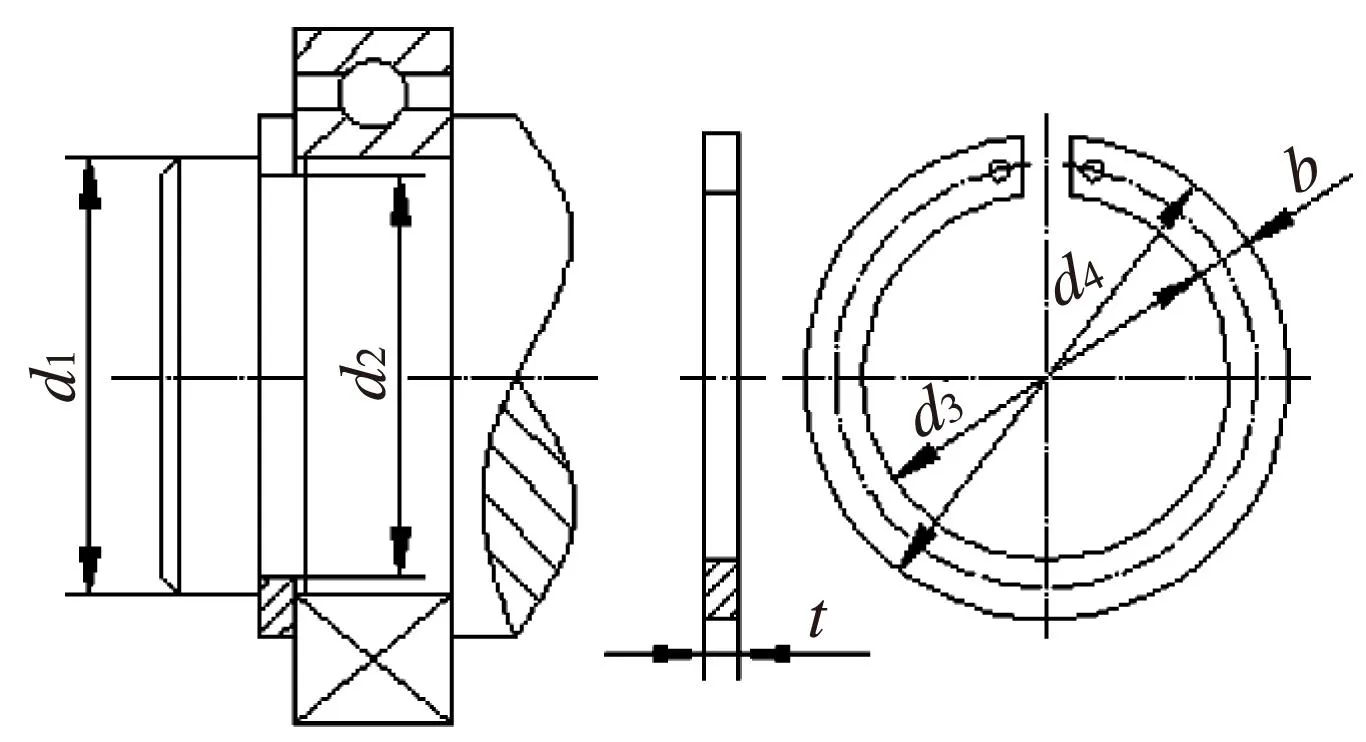
图1　轴用弹性挡圈工作结构示例

本文通过建立单一旋转离心力作用下挡圈受力模型，通过微积分对挡圈模型进行受力分析，给出了在离心力作用下轴用弹性挡圈临界转速推导方法及计算公式，供相关设计者参考。

1轴用弹性挡圈临界转速模型分析[3，5-7]

工作状态下，轴用弹性挡圈离心力均等的分布在挡圈圆周，如图2所示，当轴转速达到弹性挡圈临界转速时，在离心力作用下，开口端F点内圈最先脱离挡圈槽底，此时弹性挡圈F点对槽底作用力为0，对应的弹性挡圈F点在离心力作用下沿y方向(半径方向)实际位移如下：

δFy=d2-d3

(1)

为计算离心力与δFy的关系，我们对图3所示半圆周上的一点B施加半径方向力P，求BF间任意点C在y方向的位移δCy。首先在AB间设定一点D，取微小长度ds，则有：

ds=rdθ

(2)

r为弹性挡圈自由状态中径

(3)

加在D点的弯曲力矩M为：

M=Prsin(β-θ)

(4)

根据挠曲线近似微分方程，求得在弯曲力矩M作用下ds的微变形di为：

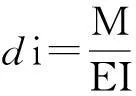
(5)

其中：E为挡圈材料弹性系数，单位kg/mm2；

I为挡圈惯性矩，单位mm4：

(6)

将公式(2)(4)带入公式(5)可得：

(7)

根据di，C点在y方向位移成分为：

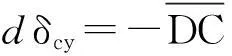
(8)

将公式(7)带入公式(8)并积分，可得点C在y方向位移分量δcy如下：

(9)

由于弹性挡圈实际所受离心力全周均等分布，其作用于圆周上的微小长度ds的离心力可用下式表示：

(10)

式中：ρ为材料密度，单位kg/mm3；

A为挡圈截面积，单位mm2

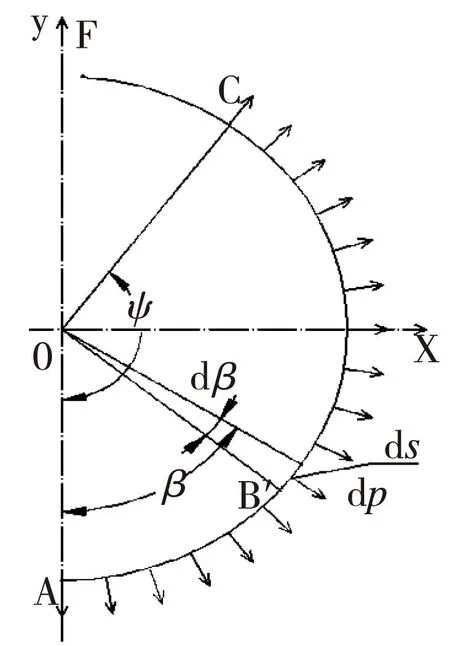
图4　受离心力时 挡圈状态

A=bt

(11)

g为重力加速度，单位mm/s2；

ω为挡圈旋转角速度，单位rad/s

(12)

nc为挡圈旋转转速，单位rpm。

如图4所示，根据作用于AC间的离心力，在AC间任意点B1取ds(=rdβ),作用于其中的离心力为：

(13)

根据dP的C点位移，将公式(13)代替P代入公式(9)，并进行积分，得到：

(14)

同理，可算得CF间离心力作用在C点的位移如下：

(15)

这样，根据全周作用的离心力，C点的位移为公式(14)与(15)之和，由此可得：

δcy=δ1cy+δ2cy

(16)

2轴用弹性挡圈临界转速公式的导出

在公式(16)中，另ψ=π，得到开口部位F沿y方向的位移为：

(17)

将公式(3)(6)(11)(12)及δcy=d2-d3代入公式(17)，整理得到轴用弹性挡圈临界转速计算公式为：

(18)

式中，取g=98 000mm/s2，E=21 000kg/mm2，ρ=7.85×10-6kg/mm3，则有：

(19)

3应用实例

图5　某型号推土机变速 箱输入端使用实例

以国内市场占有率最高的某型号推土机变速箱输入轴联轴节支撑轴承处轴用弹性挡圈设计为例进行说明，如图5中件1所示，为上述轴用弹性挡圈，其尺寸为：d3=103.8，d4=119.8， b=8，槽尺寸d2=106，材料为65 Mn。

根据公式19，其极限转速为nc=5 063 rpm，而根据此产品相关参数，该处最高转速为2 050 rpm，安全系数为S=5063/2050=2.4。满足使用要求。

在轴系结构中，应校核其松动转速，若轴系最高工作转速大于其松动转速，或安全系数过小，应修改轴系结构设计(尺寸)，根据临界转速计算式(19)，增大弹性挡圈内外径差值或增大槽底径与挡圈内径差值，均可以提高其松动转速。

4总结

轴用弹性挡圈在轴系设计中所占比重很小，但一旦发生脱落造成的损失较大，所以，应对其所能承受的临界转速进行校核计算，结合使用工况，选择合理的安全系数，使设计满足使用要求。

参考文献

[1]濮良贵，纪名刚．机械设计[M]．北京：高等教育出版社, 2006

[2]徐超．轴用弹性挡圈工作的松动转速分析计算[J]．现代机械，2003(6)：27，42

[3]汪曾详，魏先英，刘祥至． 弹簧设计手册[M]．上海：上海科学技术文献出版社,1986

[4]Seeger orbis Ltd. The SEEGER handbook[M]．Germany,2007

[5]闻邦椿．机械设计手册[M]．北京：机械工业出版社,2012

[6]刘鸿文．材料力学[M]．北京：机械工业出版社,2011

[7]冯引利，何云，陈伟．轮盘径向破裂转速计算方法分析及修正[J]．航空动力学报，2014，29(11)：2729-2734