浅析Navier—Stokes方程组的无量纲化

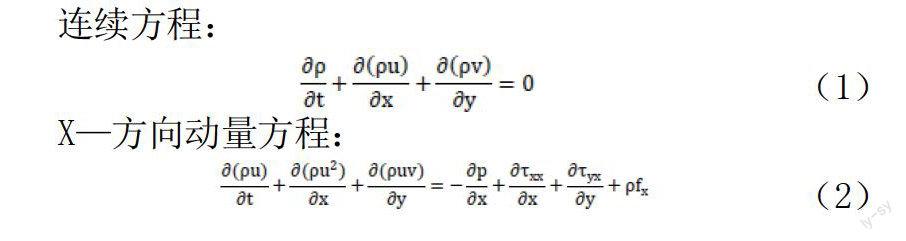
摘要：计算流体力学的控制方程通常认为是NS（Navier-Stokes）方程组，包含了能量方程、动量方程、连续性方程等方程组的总称，但NS方程组是复杂的方程组，在数值求解NS方程组之前需要对方程组进行无量纲化处理来简化计算。文章给出了非定常、二维可压缩黏性守恒NS方程组，并对NS方程组无量纲化进行了浅析。

关键词：Navier-Stokes方程组；无量纲化；计算流体力学；能量方程；动量方程；连续性方程 文献标识码：A

中图分类号：TP391 文章编号：1009-2374（2016）03-0061-02 DOI：10.13535/j.cnki.11-4406/n.2016.03.031

1 非定常、二维可压缩黏性守恒NS方程组

黏性流动包括很多种现象，比如摩擦、质量扩散和热传导等运输现象。这些运输现象在流动中是耗散的，总是会增加流动的熵。如果流动中存在不同的化学组成成分而产生浓度梯度，将发生质量扩散，比如几种不发生反应的气体混合物，例如高温流体通过高超声速飞行物体时会发生空气电离。这种流动由于不同的地方温度以及压强不同，所以导致不同流动区域会产生各种不同形式或者不同速率的反应。

为简单起见，我们这里不讨论这类形式流动，即不讨论由于流动中产生化学反应使得流动变得复杂，从而使问题变得模糊而复杂的问题，因此流体方程组不包含质量扩散方程。首先直接给出非定常、二维可压缩黏性守恒NS方程组：

式（1）至式（4）这四个方程即为二维、非定常、黏性可压缩Navier-Stokes方程组，这些方程都是耦合的偏微分方程组。所以要想得到它们的解析是非常困难的，因此我们有必要对这些方程进行无量纲化处理，然后再找出并分析方程中对流动产生影响很小的那些流动项再进行适当取舍。

四个方程有五个未知量ρ、p、u、v、e，因此需要再补充一个方程。为此我们考虑气体为完全气体，那么它的状态方程为：

参考文献

[1] 姚朝晖，周强.計算流体力学入门[M].北京：清华大学出版社，2012.

[2] 闫超.计算流体力学方法及应用[M].北京：北京航空航天大学出版社，2006.

[3] U Ghia，K.N Ghia，C.T Shin High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method.

[4] Cebeci T，Cousteix J.Modeling and Computation of Boundary Layer Flows[M].New York：Springer，1999.

[5] Davis R T.Numerical solution of the hypersonic viscous shock-layer equation[J].AIAA J，1970，8（5）.

[6] Rudman S，Rubin S G.Hypersonic viscous flow over slender bodies with sharp leading edges[J].AIAA J，1968，6（10）.

[7] 高智.简化Navier-Stokes方程组及无黏和黏性边界层联立求解[J].力学学报，1982，14（6）.

[8] 涂国华，袁湘江，查俊，等.二维抛物化稳定性方程的特征分析[J].航空学报，2009，（30）.

[9] 高智.简化Navier-Stokes方程的层次结构及其力学内涵和应用[J].中国科学A辑，1988，（6）.

[10] 王汝权，申义庆.抛物化Navier-Stokes方程数值解法评述[J].力学进展，2005，（4）.

作者简介：王敞亮（1987-），男，河北石家庄人，广东海洋大学寸金学院助教，理学硕士，研究方向：计算流体力学。

（责任编辑：陈 洁）