钢框架梁柱节点子结构抗冲击力学性能有限元仿真研究

第一作者王宁男，硕士，1988年生

通信作者霍静思男，博士，教授，1970年生

钢框架梁柱节点子结构抗冲击力学性能有限元仿真研究

王宁，陈英，霍静思

(湖南大学教育部建筑安全与节能重点实验室，长沙410082)

摘要：基于有限元软件ABAQUS对钢框架节点(全焊节点和栓焊节点)进行了非线性动态响应数值仿真模拟分析，模型合理考虑了螺栓预紧力、接触、非线性大变形及应变率效应等因素。采用该模型模拟梁柱节点子结构抗冲击试验，分析结果表明，采用显示求解器可获得较好精度和稳定性，有限元模拟的破坏模态、冲击力和位移时程曲线等结果与试验结果吻合良好。在大变形下过焊孔趾部是节点应力集中最显著的部位，是整个构件破坏的起始点。通过仿真分析，可获得梁柱节点子结构在冲击荷载作用下的动态响应和内力发展过程，该数值分析方法为深入研究钢结构抗倒塌工作机理并为合理评估其抗倒塌变形和耗能能力提供依据。

关键词：梁柱节点；有限元；动力性能；延性；应变率效应

基金项目：国家自然科学

收稿日期：2013-11-01修改稿收到日期：2014-01-28

中图分类号:TU392.1文献标志码：A

FE analysis on dynamic behaviors of beam-column connection in steel frame

WANGNing,CHENYing,HUOJing-si(China Ministry of Education Key Laboratory of Building Safety and Energy Efficiency, Hunan University, Changsha 410082, China)

Abstract:Two kinds of widely used steel anti-moment connections (welded unreinforced flange-welded web and welded unreinforced flange-bolted web) were modeled by using the finite element software ABAQUS, taking the effects of bolt pretension force, contact, nonlinear large deformation and strain rate into consideration. The model was used to simulate beam-column substructures under impact load, and it shows that ABAQUS/explicit solver presents high precision and good stability. As a result, the finite element results of failure mode and time histories of impact load and deformation agree fairly well with experimental results. Under large deformation, the most significant stress concentration locates at the weld access hole, where initiates the whole component failure. The dynamic response and internal force development of beam-column substructures were obtained by simulation analysis. The results of numerical analysis provide a basis for studying the working mechanism of progressive collapse of steel structures and for rationally accessing the ability of resisting collapse deformation and energy dissipation.

Key words:beam-column connection; finite element simulation; dynamic behavior; ductility; strain rate effect

近年来，火灾、地震以及爆炸、恐怖袭击事件的频繁发生，使得局部结构或构件的失效而引起整体结构连续倒塌事故明显增多。从1968年Ronan Point公寓连续性倒塌到2001年美国世贸中心发生整体坍塌，均由非常规荷载引起，导致关键部位失效从而引起结构局部或整体倒塌。事故发生后调查了结构倒塌的原因[1-2]，相关部门陆续出台并完善了连续倒塌规范[3-4]，其中抗倒塌设计中最主流的设计方法是荷载路径转换法(APM)，其允许结构关键构件失效，结构通过额外的传力路径来实现荷载的重分布，进而避免连续倒塌。有学者采用理论解析法推导了均布荷载作用下常温约束钢梁[5-6]和高温下约束钢梁[7]的悬链线效应发展，Lee等[8]基于能量法提出了多层钢框架结构在底层中柱失效后的抗倒塌反力，然而大变形下梁的内力发展非常复杂，使得理论公式繁琐，不同发展阶段的计算精度也有差异，且均为静力分析，忽略了结构的动力响应。有限元分析不仅可以考虑材料非线性和几何非线性，还可以进行结构动态分析，是一种准确有效的分析方法。Yin等[9-10]采用数值法对各自所提的理论计算模型进行验证；Kim等[11-12]用数值法模拟了抗震梁柱节点延性对结构抗倒塌的影响，以上分析方法均基于非线性静力分析。李海旺等采用有限元软件LS-DYNA模拟了爆炸荷载作用下平面钢框架[13]和空间钢框架[14]的动态响应和破坏过程。

由于试验条件的限制，结构抗倒塌试验研究成果较少，且以局部构件的静力加载为主[15-16]，对结构动力响应估计不足。霍静思等[17-18]分别对约束钢梁和钢框架梁柱子结构进行了冲击试验，由于试验技术的制约，部分试验数据如截面内力等很难测得。Karns[19]试验研究了爆炸荷载作用时高应变率和爆炸气流压强情况下钢框架节点的抗倒塌性能，并借助有限元软件LS-DYNA对试验过程中结构的动态响应进行模拟。

虽然有研究者开展钢框架结构抗爆荷载作用下的动态反应分析，但尚无基于荷载路径转换法(APM)的动态非线性有限元方法对结构抗连续倒塌性能至关重要的钢结构节点的动态响应和抗倒塌受力机理研究。本文运用有限元软件ABAQUS对文献[18]中扇形过焊孔的钢框架节点(全焊节点和栓焊节点)子结构进行有限元数值仿真分析，通过建立合理的非线性动态有限元模型并采用合理的非线性动态求解方法，进行了钢框架梁柱节点子结构非线性动态响应分析。通过与试验结果对比，验证有限元模型的准确性，并分析两种节点构件在冲击荷载作用下的破坏机理、延性性能以及内力转化等。

1有限元模型

1.1有限元模型的建立

(1)

文献[18]中节点及文献[17]中约束钢梁(HR5-6)的尺寸等参数见表1，fy、fu分别为钢材的屈服强度和极限强度，E为弹性模量，L为试件的长度。由文献[18]中节点破坏形式可知，变形主要发生在试件跨中短柱两侧的钢梁，钢梁端部几乎没有变形。为提高计算效率，采用B32二次完全积分梁单元模拟钢梁端部，跨中节点采用C3D8R六面体8结点减缩积分单元，梁单元与实体单元连接处用动态耦合约束模拟内力的传递，栓焊节点的有限元模型见图1，限制构件两端三个方向的位移约束，允许其平面内转动，同时约束落锤运动方向以外的两个方向位移。为提高模型的精确性，还对栓焊节点的螺栓预紧力和与连接板的接触进行模拟。鉴于锤头采用高强钢，比试件刚度要大很多，因此冲击过程中可以完全忽略锤头自身的变形，锤头建模时采用不可变形的离散壳刚体，也可降低运算量，而锤重的施加通过在刚体锤头参考点上直接施加点质量实现。

图1　栓焊节点有限元模型 Fig.1 FE model of welded unreinforced flange-bolted web connection

表1　节点详细参数

注：*表示试件断裂时的参数值

模型网格的密度大小直接影响计算精度和计算速度，经对采用不同网格尺寸的模型计算比较分析后，取钢梁单元尺寸为10 mm，螺栓单元尺寸为5 mm，由于短柱基本上处于弹性范围内，单元尺寸为20 mm，栓焊节点实体单元部分最终的网格划分见图2。

图2　栓焊节点网格划分 Fig.2 FE model mesh

ABAQUS显式求解器(explicit)是分析瞬态动力学的有效工具，用其分析全焊节点精度较好，但其不能模拟螺栓的预紧力。因此，用隐式和显式求解器分别模拟考虑螺栓预紧力和不考虑螺栓预紧力的节点，分别分析其破坏形态和应力分布情况，对比两种分析求解方法的优劣。

1.2有限元模型的验证

为验证本文有限元模型的可靠性和合理性，首先利用上述模型对霍静思等[17]约束钢梁的冲击试验HR5-6试件进行模拟，同时采用了杆系模型进行模拟。图3给出了计算冲击力-转角关系曲线，可见两种模型的计算结果均可较好的模拟约束钢梁的冲击性能，但杆系模型所计算的平台段冲击力稍大于实体模型的计算，这是由于杆系模型无法模拟上翼缘压屈，说明对于受弯大变形，梁单元的计算结果偏大，因此本文采用实体单元模拟局部变形较大的跨中节点，采用杆系单元模拟梁远端，以求得到更好的计算结果。图4为实体模型计算的跨中局部变形对比，从中可以看出，模拟结果与有限元结果吻合的较好。采用C3D8R单元的实体模型能够准确模拟钢梁跨中的局部变形。文献[17]主要研究钢框架在柱失效后钢梁的悬链线形成机理，未考虑节点对抗倒塌性能的影响。本文有限元模型主要针对两种不同节点构造对梁柱子结构受力性能的影响进行分析。

图3　试件HR5-6冲击力-转角曲线对比 [9] Fig.3 Verification of impact-rotation curves of HR5-6 [9]

图4　试件HR5-6实体模型跨中变形对比 [9] Fig.4 Midspan deformation comparison of HR5-6 [9]

2有限元结果分析

2.1节点破坏形态

图5为全焊节点试件WFWW①有限元计算与试验的跨中变形对比，图5(b)为有限元计算的冲击结束后塑性应变云图。可以看出，有限元的计算变形与试验变形吻合良好，钢梁上翼缘只有轻微压屈，截面中性轴稍有上移。从应变云图来看，钢柱完全处于弹性范围内，并未产生塑性应变。试件的塑性区域(浅色部位)主要集中在梁柱节点区域，且在实体模型范围以内，并未扩展到杆系模型部分。应变集中部位主要出现在节点附近的上下翼缘处，且应变最大值(0.071)出现在节点下过焊孔趾部(画圈部位)。可以预见，随着变形的继续增加，过焊孔趾部将首先发生破坏，是整个试件破坏的起始点。

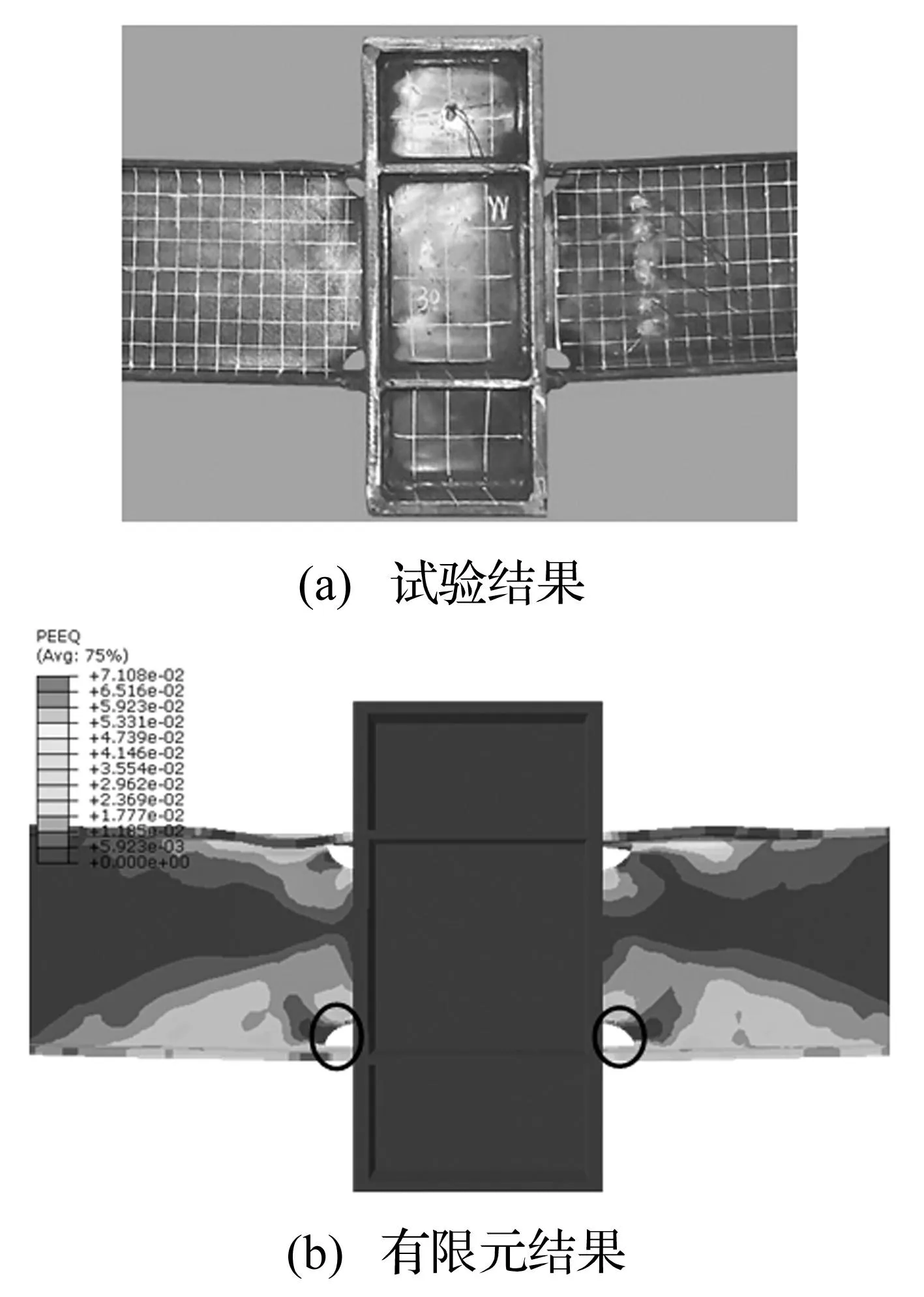
图5　试件WFWW①变形对比 Fig.5 Deformation comparison ofWFWW①

图6给出了栓焊节点试件WFBW①的模型与试验变形对比图，分别给出了ABAQUS/explicit和ABAQUS/standard求解器计算的应变云图，从图6可知，过焊孔趾部出现了与试件WFWW①类似的应力集中(画圈部位)，且外排螺栓孔的应力要明显高于内排螺栓，可以预测开裂路径应该是从过焊孔趾部衍生并扩展到腹板外排螺栓孔附近，与试验结果吻合。显式求解器的计算由于没有考虑螺栓预紧力，其最终变形要比隐式求解器要稍大，且从应变云图上看，其塑性区域更大。

从表1可知，WFBW①的冲击速度大约是WFWW①的1.5倍，冲击能量约是WFWW①的2倍，因此WFWW①的冲击变形较小，而WFBW①的冲击变形更显著。为了研究全焊和栓焊两种连接形式对节点冲击性能的影响，对全焊节点模型施加与栓焊节点相同的速度和冲击能量，分析其变形和应力集中情况。图7为相同冲击速度和冲击能量条件下，全焊节点的局部变形图，与图5分析结果相比，冲击能量增大使得梁上翼缘屈曲变形增大，应变发展范围更广，最大应变从0.071增大为0.1276，仍发生在下过焊孔趾部，假设材料的失效应变为0.2[22]，则全焊节点在相同冲击能作用下没有发生断裂，此时节点极限转角为0.083。与栓焊节点下翼缘断裂相比，全焊节点在冲击荷载作用下的延性更好。

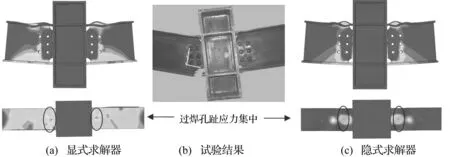
图6　试件WFBW①变形对比 Fig.6 Deformation comparison of WFBW①

图7　WFWW①的等效应变分布图 Fig.7 Equivalent strain distribution of WFWW①

2.2冲击力和位移时程曲线

图8和图9分别给出了两个试件冲击力和位移时程曲线，以及冲击力与转角关系曲线。全焊节点WFWW①仅运用ABAQUS显示求解器计算，用隐式和显式求解器分别模拟栓焊节点WFBW①考虑螺栓预紧力和不考虑螺栓预紧力的冲击性能。通过与试验所得曲线对比可知，全焊节点的有限元模拟结果与试验结果基本一致；而栓焊节点的隐式求解曲线波动较大，显式求解曲线相对较光滑，且与构件断裂前的冲击力平台值很接近，位移时程曲线吻合度也更高。

冲击力和位移时程曲线可分为三个阶段：接触阶段、稳定阶段和反弹阶段(撕裂阶段)。①接触阶段主要表现为冲击力的波动，在落锤和构件接触瞬间由于巨大的惯性力出现尖峰，位移在此阶段基本上是线性增加；②稳定阶段冲击力波动较小，称这一阶段的冲击力平均值为Fp，两个节点断裂前的冲击荷载平台值几乎相同均为240 kN左右，即在断裂前两种节点的强度和刚度几乎相同，栓焊节点断裂后，刚度迅速衰退，承载能力也随之下降；③反弹阶段以最大位移处为起始点反向运动，冲击力逐渐归零，并伴随着能量的释放，而撕裂节点以开裂位移为起点，承载力快速退化。试验结果和显式求解结果三个阶段的分界点见图8、图9。

表1还列出了两个节点和约束钢梁的极限转角及耗能，约束梁的极限转角和耗能明显大于梁柱节点的，说明梁柱节点的转动能力相比约束梁较差，从而也限制了其耗能能力。相同冲击能量作用时，全焊节点的极限转角(0.083)明显大于栓焊节点的(0.047)，即全焊连接节点在冲击荷载作用下有更好的转动能力。M为冲击质量，v为冲击速度，Ek为冲击能量，φtm、φfm分别为构件试验和有限元极限转角值，Et、Ef分别为构件试验和有限元耗能值，由冲击力—位移关系曲线积分得到，其中试件WFBW①的耗能值为断裂之前的耗能量。

图8　试件WFWW① Fig.8 TheWFWW① connection

图9　试件WFBW① Fig. 9 TheWFWW① connection

2.3塑性铰截面内力分析

为了明确比较梁柱节点的抗冲击性能和抗倒塌机理，需要分析梁柱节点子结构在大变形下的内力发展机制。钢梁塑性铰是结构最先进入塑性的区域，其截面的内力转换关系到整个结构的荷载分配。由于试验技术的限制，无法精确测试塑性铰截面内力变化，因此采用有限元模型对塑性铰截面内力发展进行分析。图10给出了栓焊节点和全焊节点模型塑性铰截面的弯矩(M)和轴力(N)随着节点转角的发展曲线，并与文献[17]中相同截面尺寸的约束钢梁(HR5-6)在冲击荷载作用下跨中截面内力进行对比，其中Mp和Np分别为塑性铰截面的全塑性弯矩和全塑性轴力，转角φ为跨中位移与构件半跨长度的比值。从图10可知，两种梁柱节点塑性铰弯矩和约束梁跨中弯矩发展曲线在弹性段几乎重合，这是因为三个模型的弹性段抗弯刚度基本相同，轴力在此阶段发展不明显，几乎为零；进入塑性之后截面弯矩稍微增大，但根据冲击能量和冲击速度的不同截面弯矩峰值也不一样，之后弯矩缓慢下降，而轴力逐渐增大，直到达到最大转角。梁柱节点塑性铰处的弯矩和约束钢梁跨中弯矩均未达到全截面塑性弯矩，约束钢梁在冲击作用下的转动能力和延性最好，最大转角达到0.11。由于抗震设计的构造要求，过焊孔不仅对梁截面有一定削弱，冲击作用下过焊孔趾部存在较大塑性应变(见图4)，有脆性破坏的趋势，构件WFBW①的断裂即始于下过焊孔趾部。

图10还给出了Lee等[8]静力荷载作用下约束钢梁内力发展曲线，本文节点模型的钢梁跨高比L/D=10，因此只对比这一种尺寸的约束钢梁内力曲线。当L/D=10时，静力荷载作用下试件转角在达到0.1之前没有出现塑性铰弯矩的明显下降，对应轴力约为0.3倍塑性轴力；冲击荷载作用下约束钢梁在转角为0.1时对应的轴力为0.15倍塑性轴力， 其内力只发展到文献[5]静力模型的第二阶段，构件仍然主要依靠抗弯承载，悬链线效应并未充分发展。进入塑性后冲击作用下的截面轴力比和弯矩比曲线与静力作用时几乎成平行线发展，即发展趋势基本一致。

图10　截面内力发展曲线 Fig.10 Internal force development curves

3结论

本文运用非线性有限元软件ABQUS对全焊节点和栓焊节点梁柱子结构进行了模拟，并对比了有限元模型与试验的破坏模态、冲击力和位移时程曲线以及转角和耗能情况，验证了模型的准确性。通过有限元模拟结果的对比分析，得出以下结论：

(1)通过有限元结果与试验结果对比可知，节点失效之前的破坏形态、冲击力和位移时程曲线以及转角和耗能与试验结果吻合的较好，即所建立的有限元模型可以准确的模拟构件在冲击荷载作用下的动力性能；

(2)对于全焊节点，显式求解器可以较准确的模拟其破坏形态及冲击力发展；对于栓焊节点，采用隐式求解法可以较准确的预测塑性应变最大的部位，即整个构件破坏的起始点，但冲击力和位移时程曲线波动较大，显式求解结果更稳定；

(3)通过有限元分析可知，相同冲击速度和冲击能量作用下，全焊节点的转动能力和延性比栓焊节点好，因此耗能能力也较强；然而当转角较大时，两种节点均在过焊孔趾部发生较大的塑性应变，是裂纹的起源；

(4)梁柱节点子结构的转动变形能力明显小于约束梁，在转角较小时就发生局部破坏，从而限制了悬链线效应的发展，塑性铰处最终的轴力占塑性轴力的20%以下，构件以抗弯承载为主；

(5)冲击荷载作用下梁柱子结构的内力发展趋势与静力的相同，但截面内力转化机制有一定的区别，静力分析的构件塑性铰轴力比和弯矩比都偏大。

参考文献

[1]Pearson C, Delatte N. Ronan point apartment tower collapse and its effect on building codes[J]. Journal of Performance of Constructed Facilities, 2005, 19(2): 172-177.

[2]Bazant Z P, Zhou Y. Why did the world trade center collapse?-simple analysis[J]. Journal of Engineering Mechanics, 2002, 128(1): 2-6.

[3]Administration G S. Progressive Collapse Analysis and Design Guidelines for New Federal Office Buildings and Major Modernization Projects[S]. Washington D.C., U.S.A ., 2003.

[4]Department of Defense. Design of Buildings to Resist Progressive Collapse[S]. UFC 4-023-03, Washington D.C., U.S.A ., 2005.

[5]Izzuddin B A. A simplified model for axially restrained beams subjected to extreme loading[J]. International Journal of Steel Structures, 2005, 5: 421-429.

[6]王开强, 李国强, 杨涛春. 考虑悬链线效应的约束钢梁在分布荷载作用下的性能(Ⅰ)-理论模型[J]. 土木工程学报, 2010, 43(1): 1-7.

WANG Kai-qiang, LI Guo-qiang, YANG Tao-chun. A study of restrained steel beams with catenary action under distributed load-Part I: theoretical model[J]. China Civil Engineering Journal, 2010, 43(1): 1-7.

[7]Yin Y Z, Wang Y C. Analysis of catenary action in steel beams using a simplified hand calculation method, Part 2: validation for non-uniform temperature distribution[J]. Journal of Constructional Steel Research, 2005, 61(2): 213-234.

[8]Lee C H, Kim S, Han K H, et al. Simplified nonlinear progressive collapse analysis of welded steel moment frames[J]. Journal of Constructional Steel Research,2009,65(5):1130-1137.

[9]Yin Y Z, Wang Y C. Analysis of catenary action in steel beams using a simplified hand calculation method, Part 1: theory and validation for uniform temperature distribution[J]. Journal of Constructional Steel Research, 2005, 61(2): 183-211.

[10]李国强, 王开强, 杨涛春. 考虑悬链线效应的约束钢梁在分布荷载作用下的性能(Ⅱ)-数值算例验证[J]. 土木工程学报, 2010, 43(1): 8-12.

LI Guo-qiang, WANG Kai-qiang, YANG Tao-chun. A study of restrained steel beams with catenary action under distributed load-Part Ⅱ: numerical verification[J].China Civil Engineering Journal, 2010, 43(1): 8-12.

[11]Kim T, Kim J. Collapse analysis of steel moment frames with various seismic connections[J]. Journal of Constructional Steel Research, 2009, 65(6): 1316-1322.

[12]Khandelwal K, EI-Tawil.Collapse behavior of steel special moment resisting frame connections[J]. Journal of Structural Engineering, 2007, 133(5): 646-655.

[13]李海旺, 薛飞, 秦东祺. 爆炸荷载作用下平面钢框架变形形态研究[J]. 工程抗震与加固改造, 2005, 27: 155-161.

LI Hai-wang, XUE Fei, QIN Dong-qi. Study of plane steel frame deformation patten under explosion load[J].Earthquake Resistant Engineering and Retrofitting, 2005, 27: 155-161.

[14]李海旺, 李彦君. 爆炸荷载作用下空间钢框架破坏过程分析[J]. 太原理工大学学报, 2007, 38(3): 259-263.

LI Hai-wang, LI Yan-jun.Fracture analysis of steel frame-structure under explosion load[J]. Journal of Taiyuan University of Technology, 2007, 38(3): 259-263.

[15]Yang B, Tan K H. Numerical analyses of steel beam-column joints subjected to catenary action[J]. Journal of Constructional Steel Research, 2011, 10(7): 1-11.

[16]Sadek F, Main J A, Lew H S, et al. An Experimental and Computational Study of Steel Moment Connections Under a Column Removal Scenario[S].NIST TN 1669, National Institute of Standards and Technology, Gaithersburg, MD. 2010.

[17]霍静思, 张晋清, 陈柏生,等. 冲击荷载作用下热轧H型钢梁力学性能试验研究[J]. 建筑结构学报, 2011, 32(12):19-26.

HUO Jing-si, ZHANG Jin-qing, CHEN Bo-sheng, et al. Dynamic behaviors of hot-rolled steel beams under drop weight impact loading[J]. Journal of Building Structures,2011, 32(12):19-26.

[18]王宁, 基于抗震设计和构造改进的钢框架结构抗倒塌性能研究[D]. 长沙：湖南大学，2013.

[19]Karns J E, Houghton D L, Hall B E, et al. Blast testing of steel frame assemblies to assess the implications of connection behavior on progressive collapse[C]//Proceedings of the 2006 Structures Congress, St. Louis, Missouri, U.S.A., 2006, 1-10.

[20]Symonds P S. Survey of Method of Analysis for Plastic Deformation of Structures Under Dynamic Ioading[M]. Brown Univ Providence Ridiv of Engineering, 1967.

[21]Jones N. Structural Impact[M]. Cambridge, U.K:Cambridge University Press, 1997.

[22]Munoz-Garcia E, Davison B, Tyas A. Structural integrity of steel connections subjected to rapid rates of loading[C]//Proceedings of the 2005 Structures Congress and the 2005 Forensic Engineering Symposium. New York, 2005.