考虑质量偏心Timoshenko梁的弯-纵耦合固有振动特性研究

考虑质量偏心Timoshenko梁的弯-纵耦合固有振动特性研究

王剑1,2，张振果1,2，华宏星1,2

(1. 上海交通大学机械系统与振动国家重点实验室，上海200240；2.上海交通大学振动、冲击及噪声研究所，上海200240)

摘要：针对有限元法等数值方法较难处理的质量偏心梁问题，考虑质心、形心不重合情形下的弯-纵耦合效应，建立了有偏心Timoshenko梁弯-纵耦合振动的数学模型，推导了相应的特征方程。进而给出了若干偏心工况下Timoshenko梁弯-纵耦合振动的解析表达式，并探讨了偏心率和典型边界条件对纵向和弯曲振动固有频率和模态振型的影响规律。分析结果表明，固有频率随着偏心率的增大而减小，且质量偏心对纵向振动的影响较弯曲振动更为明显。

关键词：质量偏心；弯-纵耦合；Timoshenko梁；振动

中图分类号:O326；U661.44

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.003

Abstract:Natural vibration of a beam with mass eccentricity is difficult to deal with using numerical methods, such as, the finite element method. Considering the coupling effect caused by the center of mass not coinciding with the center of geometry, the mathematical model of a Timoshenko beam’s flexural-longitudinal coupled vibration was established, the corresponding characteristic equation was derived. Then the analytic solutions to Timoshenko beam’s flexural-longitudinal coupled natural vibration under several mass eccentric conditions were deduced. The effect laws of eccentricities and boundary conditions on the natural frequencies and modal shapes of flexural-longitudinal coupled natural vibration were explored. The results showed that the natural frequencies decrease with increase in eccentricity, and the effects of eccentricity on the longitudinal vibration are more obvious than those on the flexural vibration.

基金项目：国家自然科学基金项目(51409128,51409129,U1430236);江苏省自然科学青年基金项目(BK20140504) 国家自然科学基金(51375047);教育部新世纪优秀人才支持计划(NCET-12-0048)

收稿日期：2015-01-26修改稿收到日期：2015-04-28 2014-04-23修改稿收到日期：2015-04-28

Flexural-longitudinal coupled natural vibration characteristics of a Timoshenko beam considering mass eccentricity

WANGJian1,2,ZHANGZhen-guo1,2,HUAHong-xing1,2(1. State Key Laboratory on Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 200240, China;2. Institute of Vibration, Shock and Noise, Shanghai Jiao Tong University, Shanghai 200240, China)

Key words:eccentricity; flexural and longitudinal coupled; Timoshenko beam; vibration

本文推导了有偏心Timoshenko梁的弯-纵耦合振动控制方程，给出了不同偏心工况下弯-纵耦合振动的解析解，并分析了偏心率和边界条件对弯-纵耦合固有振动特性的影响。

1有偏心Timoshenko梁的数学模型

如图1所示为质量偏心Timoshenko梁微元。其中，Q是剪切力、N是轴向力、M是弯矩、D是形心(刚度中心、弯曲中心)、G是质量中心、e是梁质心和形心之间的距离、γ是剪切应变、θ是转动角度、v是梁的横向位移。

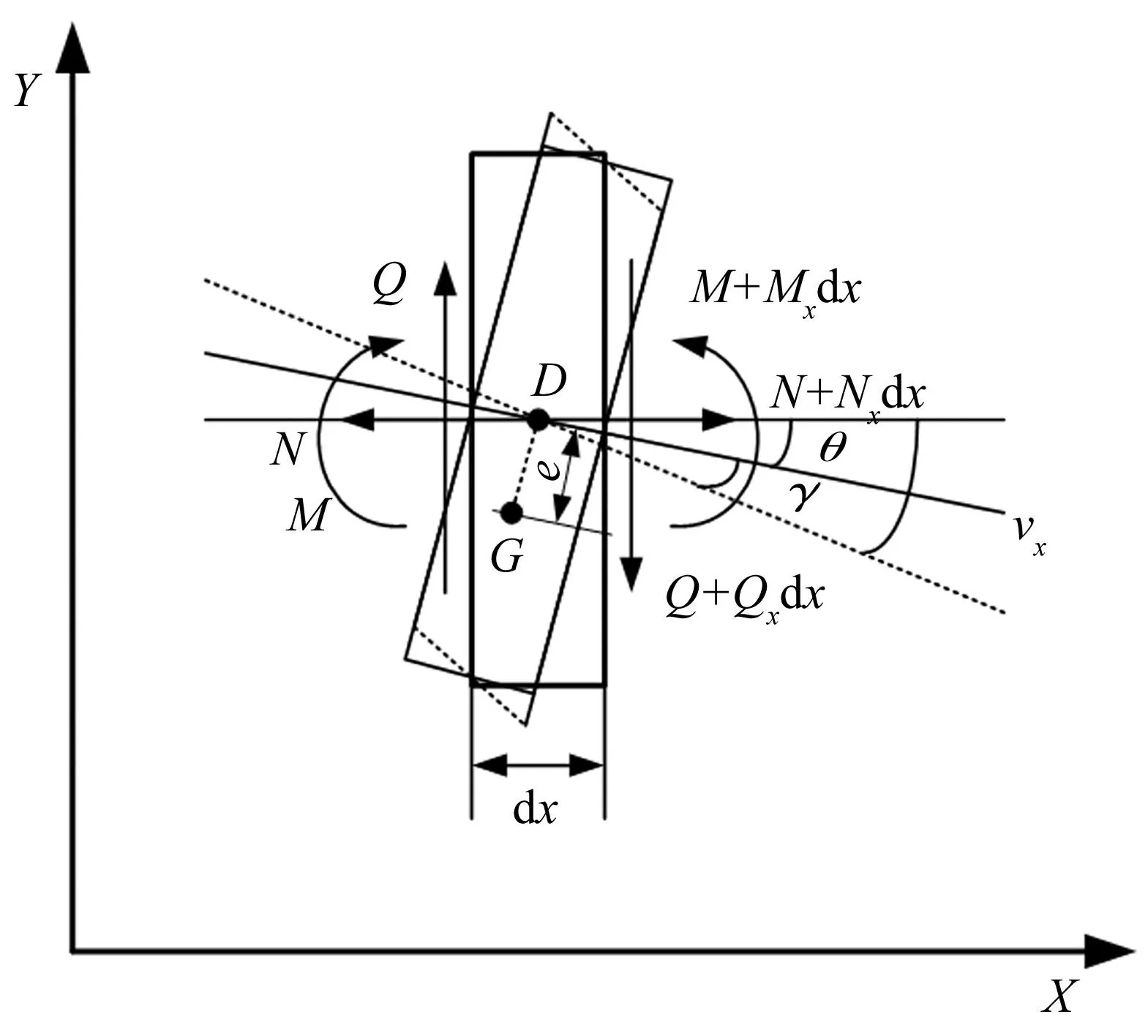
图1　质心和几何中心不重合的Timoshenko梁微元 Fig.1 Timoshenko Beam element with misalignment between centroid and geometric center

根据纵向力平衡方程：

ρA[utt+eθtt]dx=N+Nxdx-N

(1)

根据剪力平衡关系：

ρAvttdx=Q-(Q+Qxdx)

(2)

根据弯矩平衡关系：

ρ[I+Ae2]θttdx=

M+Mxdx-M-Qdx-(N+Nxdx-N)e

(3)

式中:ρ是梁的密度,A是梁的截面面积,u是梁的纵向位移,I是梁截面的截面惯性矩。本文研究对象是沿长度方向均匀的梁，因此上述梁的几何参数和物理参数沿梁的长度方向均为常数。下标t表示对变量关于t求偏导，下标x表示对变量关于x求偏导。

由于梁的质量中心和形心不重合，梁的转动将引起质心的纵向位移。而转动造成质心的横向位移属于二阶小量，可以忽略。梁微元转动引起质心的纵向位移为eθ，则质心纵向加速度可表示为utt+eθtt。同时质心的纵向运动诱使梁微元产生ρAe2dx的附加转动惯量。

应变和力之间的关系为：

N=EAux

(4)

M=EIθx

(5)

Q=-kAG(vx-θ)

(6)

式中:E是弹性模量、k是截面的剪切系数、G是剪切模量。

将式(4)～式(6)代入式(1)～式(3)，可得到：

ρA(utt+eθtt)=EAuxx

(7)

ρAvtt=kGA(vxx-θx)

(8)

ρ(I+Ae2)θtt=EIθxx+kGA(vx-θ)-eEAuxx

(9)

根据式(8)，可得到：

(10)

根据式(10)，可得到：

(11)

(12)

将式(7)、式(9)对x求一阶偏导：

ρA(uttx+eθttx)=EAuxxx

(13)

ρ(I+Ae2)θttx=EIθxxx+

kGA(vxx-θx)-eEAuxxx

(14)

将式(10)～式(12)代入式(13)、式(14)，化简可得考虑质量偏心Timoshenko梁的弯-纵耦合控制方程：

ρ2evtttt-ρekGvxxtt+kGEuxxx-kGρuttx=0

(15)

ρ2(I+2Ae2)vtttt+EIkGvxxxx-[EIρ+ρkG(I+

2Ae2)]vxxtt-ρAekGuttx+kGρAvtt=0

(16)

2求解方法

利用分离变量法，可令

u(x,t)=U(x)sin(ωt+φ)

v(x,t)=V(x)sin(ωt+φ)

(17)

将式(17)代入式(15)及(16)，得到：

ρ2eω4V+ρekGω2Vxx+

kGEUxxx+kGρω2Ux=0

(18)

ρ2(I+2Ae2)ω4V+EIkGVxxxx+[EIρ+ρkG(I+

2Ae2)]ω2Vxx+ρAekGω2Ux-kGρAω2V=0

(19)

令

V(x)=CeλxU(x)=Beλx

(20)

将式(20)代入(18)、(19)，得到：

(21)

式中：

Z11=ρ2eω4+ρekGω2λ2

Z12=kGEλ3+kGρω2λ

Z21=ρ2(I+2Ae2)ω4+EIkGλ4-

kGρAω2+[EIρ+ρkG(I+2Ae2)]ω2λ2

Z22=ρAekGω2λ

式(21)有非零解的条件为系数矩阵的行列式要为零，由此可得到偏心梁纵-横耦合振动的特征方程：

E2k2G2IS3+kGEρω2(EI+2kGI+2kGAe2)S2-

kGρω2(-2EIρω2-2EAe2ρω2-kGρIω2-

kGρAe2ω2+kGEA)S-

kGρ2ω4[-(I+Ae2)ρω2+kGA]=0

(22)

式中：S=λ2。

式(22)为λ的六次方程，则其根可表示为：

故而振型函数可表示为：

V(x)=Ceλx=C1eλ1x +

C2eλ2x +C3eλ3x +C4eλ4x +C5eλ5x +C6eλ6x

(23)

U(x)=Beλx=B1eλ1x+B2eλ2x+

B3eλ3x+B4eλ4x+B5eλ5x+B6eλ6x=

H(λ1)C1eλ1x+H(λ2)C2eλ2x+H(λ3)C3eλ3x+

H(λ4)C4eλ4x+H(λ5)C5eλ5x+H(λ6)C6eλ6x

(24)

式中：

eλ1x=ch(αx)+sh(αx)，eλ2x=ch(αx)-sh(αx)

eλ3x=cos(βx)+isin(βx)，eλ4x=cos(βx)-isin(βx)

eλ5x=cos(γx)+isin(γx)，eλ6x=cos(γx)-isin(γx)

根据式(21)，B和C之间存在如下关系：

Bj=H(λj)Cj，j=1,2…6

式中：

(25)

考虑三种典型边界条件。

自由-自由梁的边界条件：

简支-简支梁的边界条件：

U=V=EIΘx=0

(27)

固支-固支的边界条件：

U=V=Θ=0

(28)

以自由-自由边界条件为例，由式(27)、(28)可得：

(29)

(30)

将式(17)代入式(10)中，可得：

(31)

对式(31)积分：

(32)

将式(31)、(32)代入式(29)、(30)，可得：

(33)

(34)

利用式(25)对式(23)、式(24)进行整理，可得：

Ux=λ1H(λ1)C1eλ1x+λ2H(λ2)C2eλ2x+

λ3H(λ3)C3eλ3x+λ4H(λ4)C4eλ4x+

λ5H(λ5)C5eλ5x+λ6H(λ6)C6eλ6x

(35)

(36)

(37)

将式(35)～式(37)代入边界条件式(26)、式(33)、式(34)，可以得到关于C1-C6的方程组表示为矩阵形式如下：

[T][C]=[0]

(38)

式中：

[C]=[C1C2C3C4C5C6]T

T11=T12=αH(α),T13=T14=βH(β),

T15=T16=γH(γ)

T21=αH(α)[sh(αL)+ch(αL)]

T22=αH(α)[ch(αL)-sh(αL)]

T23=βH(β)[-sin(βL)+icos(βL)]

T24=βH(β)[sin(βL)+icos(βL)]

T25=γH(γ)[-sin(γL)+icos(γL)]

T26=γH(γ)[sin(γL)+icos(γL)]

T是一个关于ω的矩阵，式(38)存在非零解的条件为T矩阵的行列式为零，从而可获得特征方程，并可解出梁的固有频率。将固有频率代入T中，即可求得相应的振型系数，从而得到梁的振型函数。

3算例分析

本文所采用梁模型参数见表1所示，其中剪切因子k是根据Cowper[11]对圆形截面的研究所取。为验证本文方法的正确性，首先在未考虑偏心情况下，将解析结果与ANSYS软件数值结果进行比较。其后考察各种偏心率工况下，梁的弯-纵振动特性。

表1　计算模型的参数

3.1未考虑偏心下的结果对比

以自由-自由边界条件为例，前十阶模态频率的对比如表2所示。不难看出，本文结果与有限元结果吻合良好，各阶误差均小于0.0518%，从而可验证本文方法的有效性。表2所示其中第6阶和第9阶分别对应梁的一纵和二纵固有振动。

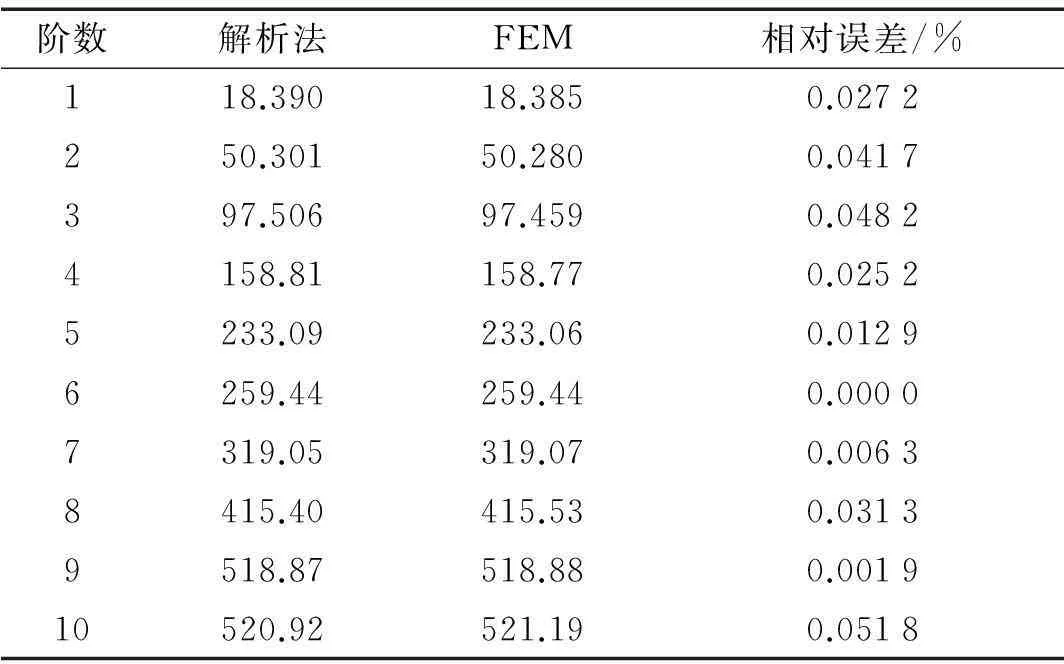
表2　未偏心下本文方法与数值方法的结果比较

相对误差：(解析法固有频率FEM固有频率)/解析法固有频率100%

3.2各种偏心率工况下的结果对比

在表3中，列出了三种典型边界，即固支-固支(C-C)、自由-自由(F-F)、简支-简支(S-S)边界条件下，偏心率ee(ee=e/R)为0、0.3、0.6和0.9工况下的梁模型前六阶固有振动频率的结果。图2、3、4为各工况下梁模型的一弯和一纵振型比较。

通过对表3中的结果对比，不难发现：除了自由-自由边界条件下的一阶纵向振动固有频率会随着质量偏心的增大略有增大以外，其它边界条件下的各阶振动固有频率都会随着偏心率的增大而降低；对于任一阶固有振动，其模态频率均会随着偏心率的增大而减小，偏心率越大，其频率下降的越明显；在任意偏心率工况下，梁模型固有振动阶数越高，其自然频率的下降越明显。

表3　三种典型边界条件下，各种偏心时梁模型的前六阶固有频率

通过对图2～图4中的振型结果比较，可以发现：质量偏心对梁模型的一弯和一纵固有振型影响均很小。相对而言，每一种边界条件下，质量偏心对一阶纵向振动振型的影响比对一阶弯曲振动振型的影响要大，见图2。

图2 固支-固支边界条件时的振型Fig.2Vibrationmodesunderclamped-clampedboundarycondition图3 自由-自由边界条件时的振型Fig.3Vibrationmodesunderfree-freeboundarycondition图4 简支-简支边界条件时的振型Fig.4Vibrationmodesundersimply-simplyboundarycondition

4结论

本文通过对质心和形心不重合Timoshenko梁的力学分析，导出了质量偏心梁的弯-纵耦合振动解析表达式。给出了三种典型边界条件下，对应于不同偏心率工况的偏心梁固有振动频率和模态振型，研究了质量偏心对梁固有振动特性的影响，主要结论如下：

(1)通过未考虑偏心情况下的解析解和有限元结果的比较，证实了本文方法的有效性；

(2)除自由-自由边界条件的一阶纵振之外，随着质量偏心的增大，系统各阶振动频率略微降低，且随着偏心率增大，频率下降越明显；在各工况下对应于任一偏心率，振动阶数越高，频率下降越明显；

(3)质量偏心对梁的一阶弯曲和一阶纵振固有振型的影响较小，相对而言，偏心对一纵振型的影响要比对一弯大。

参考文献

[1]Daidola J C. Natural vibrations of beams in a fluid with applications to ships and other marine structures[J]. Transactions-Society of Naval Architects and Marine Engineers, 1984, 92: 331-351.

[2]Klein L. Transverse vibrations of non-uniform beams[J]. Journal of Sound and Vibration, 1974, 37(4): 491-505.

[3]Auciello N M, Ercolano A. A general solution for dynamic response of axially loaded non-uniform Timoshenko beams[J]. International Journal of Solids and Structures, 2004, 41(18): 4861-4874.

[4]徐腾飞, 向天宇, 赵人达. 变截面 Euler-Bernoulli 梁在轴力作用下固有振动的级数解[J]. 振动与冲击, 2008, 26(11): 99-101.

XU Teng-fei, XIANG Tian-yu, ZHAO Ren-da. Series solution of natural vibration of the variable cross-section Euler-Bernoulli beam under axial force[J]. Journal of Vibration and Shock, 2008, 26(11): 99-101.

[5]崔灿, 蒋晗, 李映辉. 变截面梁横向振动特性半解析法[J]. 振动与冲击, 2012, 31(14): 85-88.

CUI Can, JIANG Han, LI Ying-hui.Semi-analytical method for calculating vibration characteristics of variable cross-section beam[J]. Journal of Vibration and Shock, 2012, 31(14): 85-88.

[6]Chehil D S, Jategaonkar R. Determination of natural frequencies of a beam with varying section properties[J]. Journal of Sound and Vibration, 1987, 115(3): 423-436.

[8]姚熊亮, 计方, 钱德进, 等. 偏心阻振质量阻抑振动波传递特性研究[J]. 振动与冲击, 2010,29(1): 48-52.

YAO Xiong-liang, JI Fang, QIAN De-jin. Characteristics of eccentric blocking masses attenuating vibration wave propagation[J]. Journal of Vibration and Shock, 2010,29(1): 48-52.

[10]谢基榕, 徐利刚, 沈顺根, 等. 推进器激励船舶振动辐射声计算方法[J]. 船舶力学, 2011, 15(5): 563-569.

XIE Ji-rong, XU Li-gang, SHEN Shun-gen. Calculational method for radiating sound excited by vibration of ship propeller[J]. Journal of Ship Mechanics, 2011, 15(5): 563-569.

[11]Cowper G R. The shear coefficient in Timoshenko’s beam theory[J]. Journal of Applied Mechanics, 1966, 33(2): 335-340.

第一作者崔杰男，博士，讲师，硕士生导师，1984年生

第一作者刘辉女，博士，教授，博士生导师，1975年生