超空泡航行体闭环控制动力学特性研究

第一作者熊天红女，讲师，1977年生

通信作者包伯成男，博士，教授，1966年生

超空泡航行体闭环控制动力学特性研究

熊天红1,包伯成2

(1.南京理工大学瞬态物理国家重点实验室, 南京210094; 2.常州大学信息科学与工程学院, 江苏常州213164)

摘要：通过对超空泡航行体的动力学描述，采用分段线性滑行力函数拟合复杂非线性滑行力函数，构建了超空泡航行体闭环控制动力学模型，获得以反馈控制增益为可变参数的四维混沌系统．利用相轨图、庞加莱映射、分岔图和Lyapunov指数等动力学分析工具，分析不同反馈控制增益变化时系统复杂的动力学行为。结果表明，超空泡航行体闭环控制动力学行为依赖于各个闭环控制增益，随着这些参数的变化，系统存在分岔、混沌、周期窗、共存吸引子和不完全费根鲍姆树等奇异的非线性物理现象；合理选择反馈增益，能够实现超空泡航行体的稳定航行。研究结果将对超空泡航行体反馈控制器的设计具有重要的指导意义。

关键词：分岔；混沌；闭环控制；超空泡航行体

基金项目：国家自然科学基金(51277017);江苏省自然科学基金(BK2012583);国家自然科学基金青年基金(11402116)

收稿日期：2014-05-27修改稿收到日期：2015-01-13

中图分类号:O322

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.17.028

Abstract:By describing dynamics of supercavitating vehicles and utilizing a piecewise-linear sliding force function to fit a complex nonlinear sliding force function, a closed-loop control dynamic model for a supercavitating vehicle was constructed, a four-dimensional chaotic system with feedback control gains as variable parameters was obtained. By using dynamic analysis tools, such as, phase portrait, Poincaré map, bifurcation diagram and Lyapunov exponent, the complex dynamic behaviors of the system with variation of different feedback control gains were analyzed. The results indicated that the closed-loop control dynamic behaviors of supercavitating vehicles depend on each closed-loop control gain; with these parameters’ varying, the novel nonlinear phenomena, such as, bifurcation, chaos, periodic window, co-existing attractor, imperfect Feigenbaum-tree and so on appear; the stable motion of supercavitating vehicles can be realized by choosing appropriate feedback gains. The study results provided a guidance for feedback controller design of supercavitating vehicles.

Closed-loop control dynamic characteristics for supercavitating vehicles

XIONGTian-hong1,BAOBo-cheng2(1. State Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, China;2. College of Information Science and Engineering, Changzhou University, Changzhou 213164, China)

Key words:bifurcation; chaos; closed-loop control; supercavitating vehicles

当航行体在水下高速航行时, 由于伯努利效应，使得航行体周围的液体汽化，从而产生覆盖航行体大部分表面的超空泡, 进而降低航行体在水中的阻力，大大提高了航行体的运动速度与航行距离[1-4]。超空泡航行体在水下高速航行时，航行体的尾部与空泡壁接触时会产生复杂的非线性滑行力，非线性滑行力的出现不仅会增加航行体的摩擦阻力，还会给航行体造成振动与冲击，进而产生混沌这一复杂的非线性现象[5-6]。

一个非线性动力学系统，当系统参数在一定范围内变化时，便会出现混沌和分岔等物理现象。混沌和分岔作为一种复杂的非线性物理现象,过去的几十年里在科学、数学以及工程应用等各个领域得到了研究者极大的关注，关于具体物理系统的动力学建模、非线性物理现象揭示、稳定性和分岔分析等多个方面取得了大量的研究成果[7-9]。目前国内外有关超空泡航行体的非线性动力学研究，主要是针对超空泡航行体开环参数引起的非线性现象和航行体反馈控制的研究[9-16]，有关超空泡航行体闭环控制的动力学特性研究，未见有文献报道。超空泡航行体的闭环控制特性是进行超空泡航行体反馈控制器设计的重要依据，因此完全有必要对其动力学特性进行分析和讨论。

以超空泡航行体的动力学描述为出发点，采用分段线性拟合的滑行力函数，构建超空泡航行体闭环控制动力学模型。基于此，利用常规的动力学分析工具，以反馈控制增益为可变量，揭示了超空泡航行体非线性物理现象。通过对航行体闭环控制动力学特性的分析, 合理选择反馈控制律中各个变量增益,能够实现超空泡航行体的稳定航行。

1超空泡航行体的动力学描述

航行体在水下高速航行时，周围液体汽化，从而产生覆盖航行体大部分表层的超空泡。为研究在一般情况下的空泡形态，引用反映空泡的无量纲空化数，其表达式为[1]

(1)

式中:P∞为外压，Pc为空泡内压,ρ为水的密度，V为航行体总速度。对于自然超空泡，空泡内压力可以近似认为等于水的饱和蒸汽压力Pc= 2 350 Pa。

超空泡航行体的结构和外形尺寸见图1(a)。图中长度L的航行体有两段构成：后端长度2/3L和半径R的圆柱段，以及前端长度1/3L的圆锥段。对于该航行体模型，重心(CG)距离头部为17/28L。航行体的头部有一个半径Rn的圆盘空化器。鳍舵采用十字形布局，置于航行体尾端。

航行体与空泡之间的相互作用关系可以通过作用力方程进行建模，在航行体的体坐标系中,作用在航行体上的力见图1(b), 主要有空化器上的升力Fcavitator、尾翼上的升力Ffins、尾部和空泡壁面之间相互作用产生的滑行力Fplaning，以及航行体质心位置的重力Fgravity。

图1　超空泡航行体 Fig.1 Supercavtating vehicle

超空泡航行体动力学建模的体坐标系原点位于航行体头部的圆盘空化器顶端端面的圆心, 超空泡航行体动力学建模采用四个状态变量来描述超空泡航行体的动力学，分别为垂直位置z、横向速度w、俯仰角θ和俯仰角速度q。定义横向速度w与航行体轴线垂直，定义前行速度V与航行体轴线平行。

超空泡航行体的浸没深度见图1(c)。超空泡航行体尾端的浸没深度用参数h′来表示，可表达为[13]

(2)

式中:

f(w)=2w+(w+wt0)tanh[-k(w+wt0)]+

(w-wt0)tanh[k(w-wt0)]

式中:wt0=(Rc-R)V/L为位于过渡点的正w值，k为一个用于选择控制近似误差的常数，一般有k=300，Rc为离空化器距离L处的空泡半径[13]。

按照文献[14]给出的定义式，航行体中心线与空泡中心线之间的几何角即超空泡航行体浸没角α可表达为

(3)

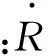
假设在航行过程中各种作用力保持平衡，航行体总速度V保持不变，由上述各参数的定义可得超空泡航行体的动力学模型如下[14]

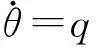
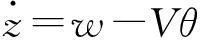
(4)

其中:m为密度比(ρm/ρ)，g为重力加速度，n为尾翼效率；各系数矩阵M0、A0、B0和重力Fgravity分别可表达为

式(4)中超空泡航行体的滑行力Fplaning可表达为

(5)

超空泡航行体设有反馈控制器，其控制输入分别为δe和δc，一般选择δe= 0、δc=kzz-kθθ-kqq，kz、kθ和kq均为实常数，分别为控制变量z、θ和q的反馈增益[10-11]。

2滑行力分段线性拟合的动力学模型

2.1滑行力分段线性拟合

超空泡航行体的系统参数值列在表1中所示[14]。基于表1的系统参数值，采用式(5)表达的非线性滑行力Fplaning，则滑行力Fplaning与横向速度w之间关系曲线如图2中的虚线所示。

表1　超空泡航行体的参数

为了便于对超空泡航行体闭环控制增益的动力学特性进行定性和定量分析，可采用一个分段线性滑行力Fp函数来拟合式(5)表示的复杂非线性滑行力Fplaning函数。这里采用了一种折衷的五段形式的分段线性滑行力函数。尽管可以采用更多段形式的分段线性滑行力函数来无限逼近非线性滑行力函数，但对系统的动力学特性影响不大，反而又增加了分析难度。

(6)

式(6)表示的分段线性拟合的滑行力Fp与横向速度w之间关系曲线如图2中的实线所示。从图2中可见，非线性滑行力Fplaning和分段线性滑行力Fp之间有着较好的拟合度。

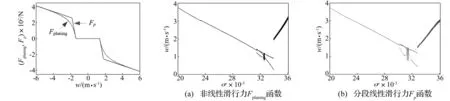
图2 Fp-w和Fplaning-w的关系曲线Fig.2CurvesofFp-wandFplaning-w图3 采用不同滑行力函数时系统(4)随σ变化的分岔图Fig.3Bifurcationdiagramofsystem(4)withdifferentplaningforcefunctions

当超空泡航行体的反馈控制增益分别为kz= 15、kθ= 30和kq= 0.3，即δe= 0、δc= 15z-30θ-0.3q时，采用非线性滑行力Fplaning函数的系统(4)随空化数σ变化的关于状态变量w的分岔图见图3(a)，而采用分段线性滑行力Fp函数的系统(4)随空化数σ变化的关于状态变量w的分岔图见图3(b)。

观察图3不难发现，两种分岔图的变化趋势是基本一致的，由此表明，采用分段线性滑行力Fp函数来拟合非线性滑行力Fplaning函数后，系统的动力学特性基本保持不变。滑行力函数的分段线性化简化了超空泡航行体的动力学模型，这对超空泡航行体的动力学特性分析具有重要的意义。

2.2超空泡航行体闭环控制的动力学模型

当系统(4)选用表1参数值，固定σ= 0.0313和δe= 0，且采用分段线性滑行力Fp函数时，可得到超空泡航行体闭环控制动力学模型为

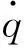
(7)

分段线性滑行力Fp函数可简化为

(8)

系统(7)的可变参数仅为三个控制增益，因此系统(7)为专用于刻画超空泡航行体闭环控制动力学行为的简单模型。

当kz= 15、kθ= 30和kq= 0.3时，系统(7)的运行轨迹即混沌吸引子在各平面上的投影见图4，相应的庞加莱映射见图5。利用Jacobi方法计算其Lyapunov指数为L1= 13.705 4,L2=-3.681 6，L3=-29.060 9和L4=-46.340 3。从系统(7)的相轨图、庞加莱映射以及Lyapunov指数可见，系统(7)为一个四维混沌系统，可生成混沌吸引子。

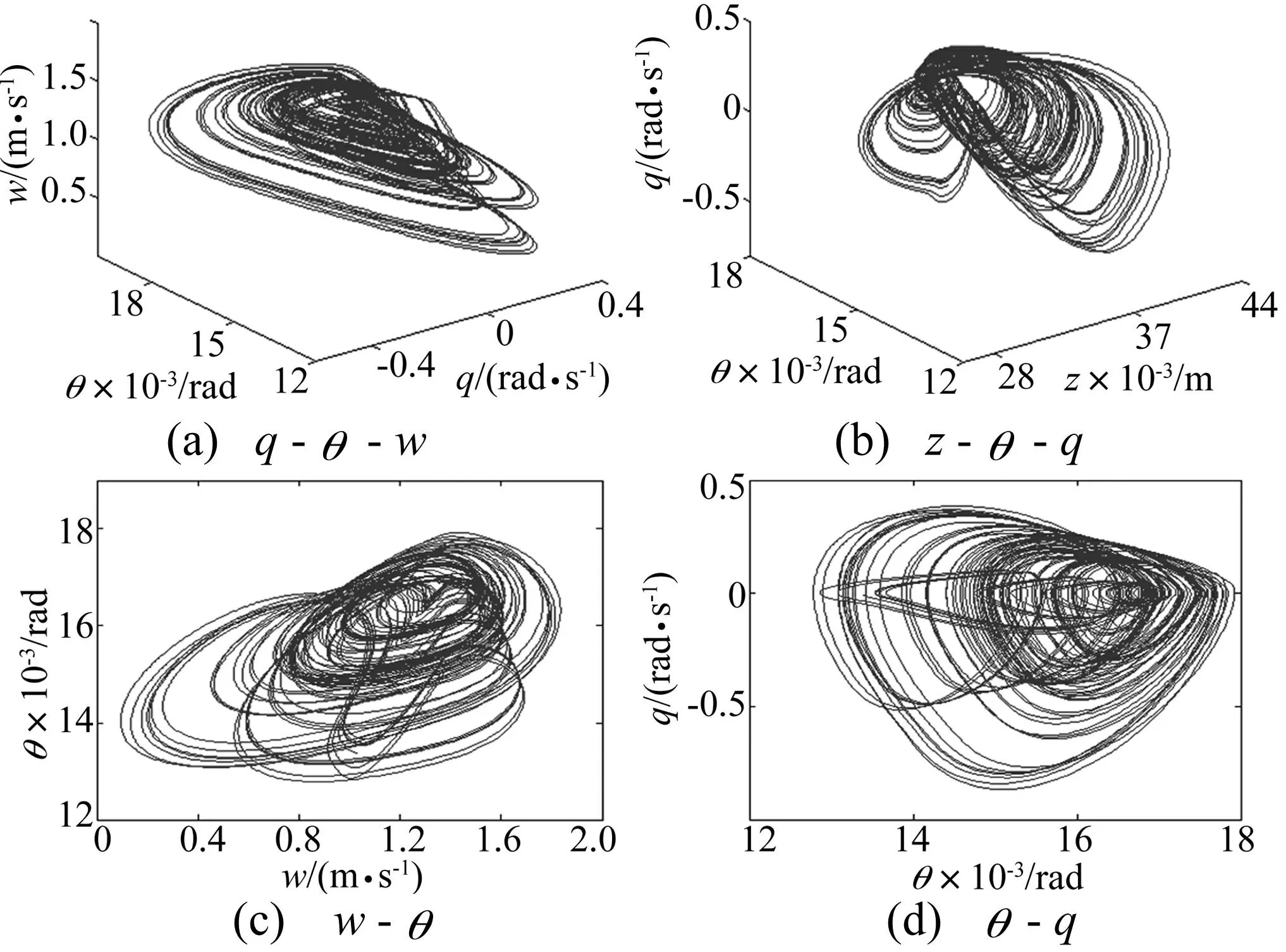
图4　混沌吸引子在相平面上的投影 Fig.4 Chaotic attractors

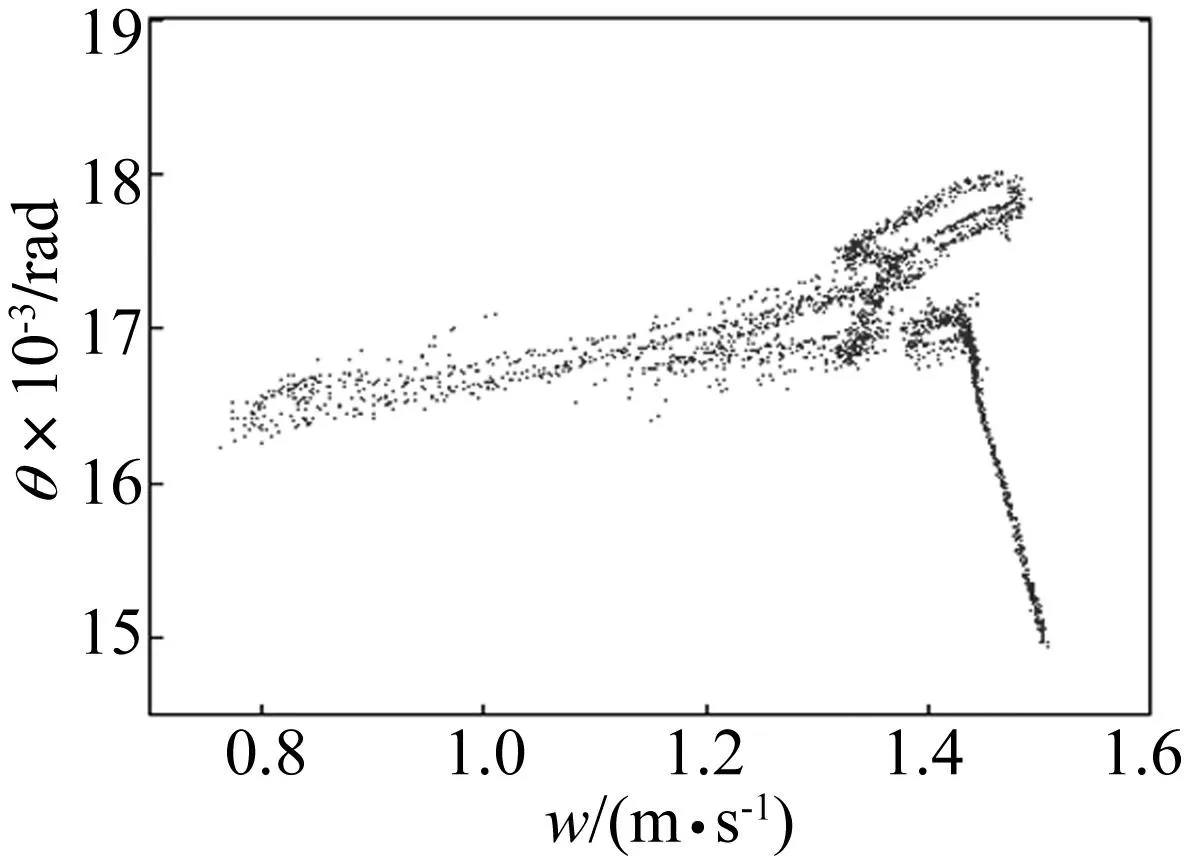
图5　庞加莱映射在w-θ平面上的投影 Fig.5 Poincaré map in w-θ plane

3闭环控制的动力学特性分析

3.1平衡点和稳定性

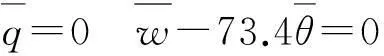
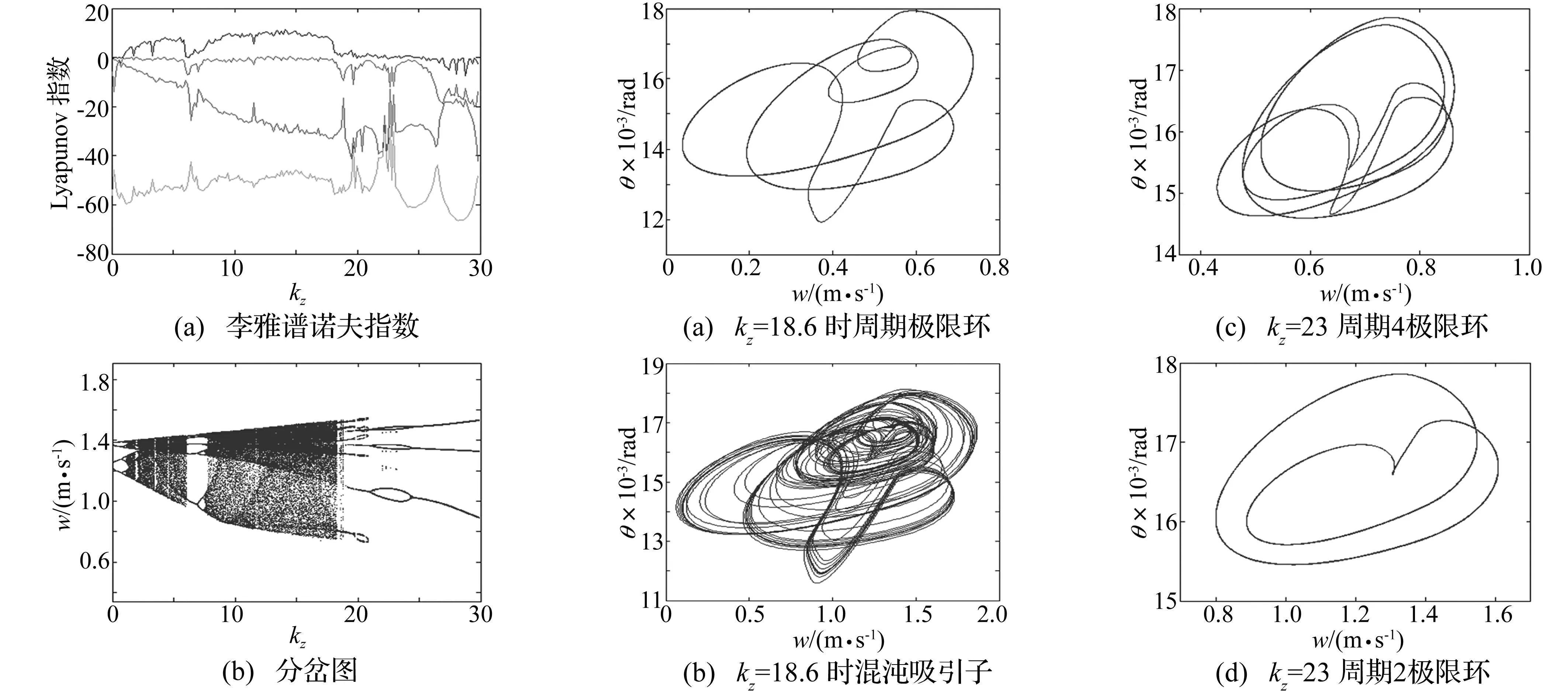
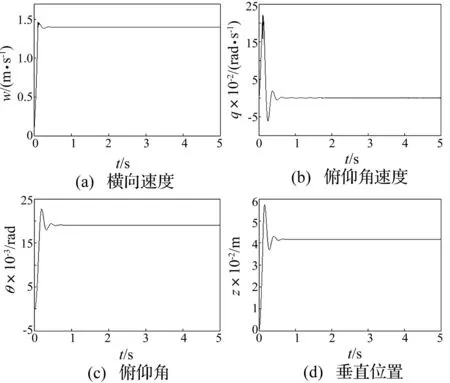
代入式(8)，可得到系统(7)随控制增益kz和kθ变化的平衡点。对于典型参数kz= 15、kθ= 30和kq= 0.3，系统(7)只在1.38

S = [1.398 6, 0, 0.019 0, 0.041 6]

把系统(7)在平衡点S处线性化，得到Jacobi矩阵为

平衡点处的特征方程为

det(1λ-JS)=0

可解得四个特征值为

λ1，2=273.59±j344.05，λ3，4=-21.13±j30.90

因此，平衡点S为不稳定鞍焦点，即指数2平衡点，满足形成混沌吸引子的必要条件。

3.2闭环控制的动力学行为

当反馈控制增益发生变化时，系统(7)有着不同的动力学行为。可利用分岔图和Lyapunov指数谱等动力学分析工具，分析系统(7)在各个反馈控制增益变化时的动力学行为。

(1)固定kθ= 30和kq= 0.3，kz在[0, 30]区间变化

系统(7)随反馈增益kz变化的Lyapunov指数谱见图6(a)，相应的状态变量w的分岔图见图6(b)。由图可见，Lyapunov指数谱与分岔图是基本一致的，kz∈[0, 18.8]时，系统(7)经倍周期分岔进入混沌状态，然后由切分岔突变到周期状态，再历经倍周期分岔后进入混沌轨道。在此区间从图5(b)可以观测到在比较宽的参数范围内，系统具有一个正值Lyapunov指数，一根零值Lyapunov指数和一根负值Lyapunov指数。在混沌区间内，系统存在多个最大Lyapunov指数小于0的周期窗，主要出现在kz= 1.95、3.45、11.7等附近。在随着反馈增益kz逐步增大，在kz∈[18.8, 30]时，系统由于混沌危机引发运行轨道状态突变，形成周期轨道，在此参数区间内最大Lyapunov指数小于或等于0。但在[21.2, 24.5]和[20.2, 21.0]的两个区间内，其运行轨迹存在不完全费根鲍姆树现象[17]，周期轨道经倍周期正分岔后，又经周期减半逆分岔回到原先的周期轨道。

另外，在一些参数值附近，系统(7)存在吸引子的共存现象。譬如，当kz= 18.6时，系统的运行轨迹在不同的初始值时会发生周期极限环与混沌吸引子的共存现象，分别见图7(a)和7(b)。

图7(a)为初始值为(0.5377, 1.833 9,-2.258 8, 0.862 2)时的周期极限环；图7(b)为初始值为(0.022 9，-0.262 0，-1.750 2，-0.285 7)时的混沌吸引子；而当kz= 23时，系统的运行轨迹在不同的初始值时有两个共存的不同周期数的极限环，分别见图7(c)和7(d)，图7(c)为初始值为(-0.001 6, 0.898 5, 0.001 8, 0.145 4)时的周期4极限环; 图7(d)为初始值为(-0.025 7, -2.329 0, 0.009 0, -0.917 8)时的周期2极限环。

(2)固定kz= 15和kq= 0.3，kθ在[0, 50]区间变化

图6 随反馈增益kz变化的动力学行为Fig.6Dynamicalbehaviorswiththevariationofkz图7 不同kz且不同初始值时w-θ平面上的相轨图Fig.7Phaseportraitswithdifferentkzanddifferentinitialvalues

系统(7)随反馈增益kθ变化的Lyapunov指数谱及相应的状态变量w的分岔图分别见图8(a)和8(b)。当kθ∈[0, 10.5]时，系统(7)以周期3轨道运行，相对应图8(a)的最大Lyapunov指数等于0。kθ逐步增大，在kθ= 10.5附近系统(7)的周期3轨道经过混沌危机直接进入混沌，最大Lyapunov指数突变为正值。并在kθ= 35.2附近系统(7)的运行轨迹经切分岔又回到周期3轨道，最大Lyapunov指数再次突变为0。kθ在[10.5, 35.2]较宽的范围内，系统(7)处于混沌状态，并存在丰富的周期窗。在[16, 16.5]和[31, 31.5]区间内，周期窗内系统(7)的运行轨迹存在不完全费根鲍姆树现象。在[16, 16.5]区间内，出现的不完全费根鲍姆树现象是周期轨道经倍周期分岔后又经减半逆分岔回到周期轨道[17]；而在[31, 31.5]区间内，出现的另一种不完全费根鲍姆树现象是周期轨道经倍周期分岔后进入混沌状态，然后又经减半逆分岔回到周期轨道。

(3)固定kz= 15和kθ= 30，kq在[0.2, 0.5]区间变化

系统(7)随反馈增益kq变化的Lyapunov指数谱及相应的状态变量w的分岔图分别见图9(a)和9(b)。当kq< 0.284时，系统(7)处于周期状态，最大Lyapunov指数等于0，并在[0.25，0.28]区间内存在不完全费根鲍姆树现象。当kq∈[0.284，0.308]时，系统(7)基本处于混沌状态，最大Lyapunov指数基本大于0，且在kq= 0.289和kq= 0.303附近存在两个较窄的周期窗。当kq>0.308时，系统(7)又回复到最大Lyapunov指数等于0的周期状态，但其运行轨迹在0.38附近出现了倍周期分岔行为，这时对应的图9(a)中的第2个Lyapunov指数从负值回到零值然后重新进入负值。

通过超空泡航行体闭环控制动力学特性分析可知，调整反馈控制律中控制增益，能够实现超空泡航行体的稳定航行。当σ= 0.031 3时，固定控制增益kz、kθ的值，增加反馈增益kq的取值范围，其状态变量w随反馈增益kq变化的分岔图见图10(a)。不难观察到，kq在[1.028 6，1.5]区间内系统平衡点的位置保持不变。如当kq=1.2时平衡点S= (1.398 6, 0, 0.019 0, 0.041 6)，系统在平衡点处线性化Jacobi矩阵的特征根为λ1，2=-63.89±j621.86，λ3，4=-9.39±j24.64，这里λ1,2、λ3,4为实部为负的共轭复根，表明平衡点S为稳定的焦点。图10(b)为系统随时间演化的Lyapunov指数谱，为清楚显示，图10(b)中仅给出三根Lyapunov指数曲线，相应的Lyapunov指数分别为L1= -8.368 2、L2=-8.676 1、L3=-65.208 9和L4=-155.486 9，其最大Lyapunov指数曲线在有限时间尺度内为负值。从系统分岔图、平衡点处特征根及Lyapunov指数可见，当控制律δc= 15z-30θ-1.2q时，系统处于稳定状态。

图11给出了控制律δc=15z-30θ-1.2q时系统响应示意图，观察图11不难发现，各个反馈控制变量初始时刻的值较大, 在反馈控制律的作用下四个状态变量逐渐稳定到其平衡点上。由此也可表明，航行体在空泡内的位置和姿态固定，处于稳定航行状态。

图8 随反馈增益kθ变化的动力学行为Fig.8Dynamicalbehaviorswiththevariationofkθ图9 随反馈增益kq变化的动力学行为Fig.9Dynamicalbehaviorswiththevariationofkq图10 δc=15z-30θ-1.2q系统动力学行为Fig.10Dynamicalbehaviorsofsysteminδc=15z-30θ-1.2q

图11　δ c = 15z-30θ-1.2q 时系统响应示意图 Fig.11 System response in δ c = 15z-30θ-1.2q

4结论

针对超空泡航行体尾部与空泡壁面接触产生的非线性滑行力，本文采用分段线性拟合的滑行力函数，构建了超空泡航行体闭环控制动力学模型，通过超空泡航行体闭环控制的非线性动力学特性的分析，得到以下结论：

(1)在一定参数范围内，利用相轨图、庞加莱映射和Lyapunov指数等数值仿真手段，验证了超空泡航行体动力学模型是以反馈控制增益为可变参数的四维混沌系统。

(2)闭环控制的超空泡航行体的运行轨迹有着复杂的动力学行为，且依赖于各个闭环控制增益；随着各个反馈增益的变化，系统出现混沌、分岔、共存吸引子和不完全费根鲍姆树等非线性现象，从而揭示了超空泡航行体运动规律的不稳定性。

(3)通过合理设置反馈控制律中各个变量增益，可以有效抑制超空泡航行体分岔、混沌等非线性现象，实现超空泡航行体的稳定航行。

参考文献

[1]Wang G, Ostoja-Starzewski M. Large eddy simulation of a sheet/cloud cavitation on a NACA0015 hydrofoil [J]. Applied Mathematical Modeling, 2007, 31: 417-447.

[2]Singhal A K, LI H Y, Athavale M M, et al. Mathematical basis and validation of the full cavitating high-speed torpedo[J]. Journal of Fluids Engineering, 2003, 125: 459-468.

[3]Li Q T, He Y S, XUE L P. A numerical simulation of pitching motion of the ventilated supercaviting vehicle around its nose[J]. Chinese Journal of Hydrodrnamics, 2011,26(6): 589-685.

[4]李代金，罗凯，党建军，等. 超空泡水下航行器空间运动建模与弹道仿真[J]. 兵工学报, 2012, 33(8): 956-961.

LI Dai-jin，LUO Kai，DANG Jian-jun，et al. Kinematic modeling and trajectory simulation for underwater supercavitating vehicles[J]. Acta Armamentarii, 2012, 33(8): 956-961.

[5]魏英杰, 王京华, 张嘉钟,等. 水下超空泡航行体非线性动力学与控制[J]. 振动与冲击, 2009, 28(6): 179-204.

WEI Ying-jie, WANG Jing-hua, ZHANG Jia-zhong,et al. Nonlinear dynam ics and control of underwater supercavitating vehicle[J]. Journal of Vibration And Shock, 2009, 28(6): 179-204.

[6]Lin G J, Balachandran B, Abed E H.Nonlinear dynamics and bifurcations of a supercavitating vehicle[J]. IEEE Journal of Oceanic Engineering, 2007, 32(4): 753-761.

[7]包伯成, 胡文, 许建平,等. 忆阻混沌电路的分析与实现[J]. 物理学报, 2011, 60(12): 120502.

BAO Bo-cheng, HU Wen, XU Jian-ping, et al. Analysis and implementation of memristor chaotic circuit[J]. Acta Physica Sinica, 2011, 60 (12): 120502.

[8]李群宏, 闫玉龙, 韦丽梅,等. 非线性传送带系统的复杂分岔[J]. 物理学报, 2013, 62(12): 120505.

LI Qun-hong, YAN Yu-long, WEI Li-mei, et al. Complex bifurcations in a nonlinear system of moving belt[J]. Acta Physica Sinica, 2013,62(12):120505.

[9]Bao B C, Xu J P, Zhou G H, et al. Chaotic memristive circuit: equivalent circuit realization and dynamical analysis[J]. Chinese Physics B, 2011, 20(12): 120502.

[10]Lin G J, Balachandran B, Abed E H. Dynamics and control of supercavitating vehicles[J]. Journal of Dynamic Control Systems, Measurement, and Control, 2008,130:021003.

[11]Nguyen V, Balachandran B. Supercavitationvechicles with noncylindrical, nonsymmetric cavities: dynamics and instabilities[J]. Journal of Computational and Nonlinear Dynamics, 2011, 6(4): 041001.

[12]Lin G J, Balachandran B, Abed E. Supercavitating body dynamics, bifurcation and control[C]. 2005 American Control Conference. Portland, OR, USA. 2005, 6: 691-696.

[13]Hassouneh M A, Vincent N, Balakumar B.Stability analysis and control of supercavitating vehicles with advection delay[J]. Journal of Computational and Nonlinear Dynamics, 2013, 8: 021003.

[14]白涛, 孙尧, 莫宏伟. 分叉分析在水下高速运动体稳定控制中的应用[J]. 哈尔滨工程大学学报, 2008, 29(10): 1067-1075.

BAI Tao, SUN Yao, MO Hong-wei. Application of bifurcation analysis to the stability control of underwater high-speed vehicles[J]. Journal of Harbin Engineering University, 2008, 29(10): 1067-1075.

[15]王京华, 魏英杰, 于开平, 等. 基于空泡记忆效应的水下超空泡航行体建模与控制[J]. 振动与冲击，2010,29(8)：160-163.

WANG Jing-hua, WEI Ying-jie, YU Kai-ping, et al. Modeling and control of underwater supercavitating vehicle based on memory effect of cavity[J]. Journal of Vibration And Shock, 2010, 29(8): 160-163.

[16]李魁彬,王安稳,邓磊.变速超空泡航行体壳结构的动力响应分析[J].振动与冲击,2013,32(4):138-141.

LI Kui-bin, WANG An-wen, DENG Lei. The influence of cavity shape on maneuvering rotational movement of supercavitating vehicle[J]. Journal of Vibration and Shock, 2013, 32(4):138-141.

[17]包伯成, 胡文, 刘中,等. DOG 小波映射伸缩和平移的动力学分析[J]. 物理学报, 2009, 29(8): 2239-2247.

BAO BO-cheng, HU Wen, LIU Zhong, et al. Dynamical analysis of DOG wavelet mapping with dilation and translation[J]. Acta Physica Sinica, 2009, 58(4): 2239-2247.