基于量子遗传算法优化RVM的滚动轴承智能故障诊断

第一作者王波男，博士生，1982年生

通信作者刘树林男，教授，博士生导师，1963年生

基于量子遗传算法优化RVM的滚动轴承智能故障诊断

王波1,2,刘树林1,蒋超1,张宏利1

(1.上海大学机电工程与自动化学院,上海200072； 2.滁州学院机械与汽车工程学院,安徽滁州239000)

摘要：提出了基于量子遗传算法(QGA)优化相关向量机(RVM)核函数参数的方法，通过仿真比较了量子遗传算法与其它方法在核函数参数优化方面的性能，结果表明基于量子遗传算法优化出的算法性能优于其它方法的优化性能。将基于量子遗传算法优化的相关向量机(QGA-RVM)应用于滚动轴承的故障诊断；采用总体平均经验模态分解(EEMD)将滚动轴承故障信号自适应地分解成多个内禀模态函数(IMF)，将IMF能量作为故障特征输入到QGA-RVM进行最终的故障诊断。结果表明，该方法能够快速准确地诊断出滚动轴承故障，验证了该方法的有效性和稳定性；此外，通过与支持向量机(SVM)的对比分析，显示了RVM在智能故障诊断应用中的优越性。

关键词：量子遗传算法;故障诊断;相关向量机;EEMD

基金项目：国家自然科学基金资助项目(51175316);高等学校博士学科点专项科研基金(20103108110006)资助项目;滁州学院规划研究项目(2014GH20)资助

收稿日期：2014-05-05修改稿收到日期：2014-10-11

中图分类号:TH212；TH213.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.17.034

Abstract:A novel method to optimize relevance vector machine (RVM)’s kernel function parameters based on the quantum genetic algorithm (QGA) was proposed. It was compared with other optimization algorithms with simulations. The results showed that the optimization method based on QGA is superior to other optimization methods. The model of RVM optimized with QGA (QGA-RVM) was applied in fault diagnosis of rolling bearings. Fault signals were decomposed adaptively into some intrinsic mode functions (IMFs) with the ensemble empirical mode decomposition (EEMD). The IMF energy as fault features was inputted into QGA-RVM for final fault diagnosis. Experimental results showed that the proposed method can diagnose rolling bearings’ faults rapidly and accurately, its validity and stability are verified; moreover, the superiority of RVM in intelligent fault diagnosis is revealed through the comparative analysis between QGA-RVM and SVM.

Rolling bearings’ intelligent fault diagnosis based on RVM optimized with Quantum genetic algorithm

WANGBo1,2,LIUShu-lin1,JIANGChao1,ZHANGHong-li1(1. School of Mechatronic Engineering and Automation,Shanghai University, Shanghai 200072, China;2. School of Mechanical and Automotive Engineering, Chuzhou Institute, Chuzhou 239000, China)

Key words:quantum genetic algorithm; fault diagnosis; relevance vector machine; ensemble empirical mode decomposition(EEMD)

在工程实际中，获取机械设备故障样本是一个难点。由于缺乏丰富的故障样本，无法使用大量故障样本训练诊断模型，在机械故障智能诊断领域涉及的通常是如何处理小样本数据问题。支持向量机(Support Vector Machine, SVM) 具有处理小样本问题的优越性、良好的泛化能力等优点，作为智能识别器在机械故障诊断领域得到了广泛的关注和研究，同时也取得了良好的故障诊断应用效果。然而，SVM也存在着一些缺点：①虽然所需的支持向量远小于训练样本数，但会随着训练样本集的增大线性增加，造成过拟合和计算时间的增加；②核函数必须满足Mercer 条件，即核函数必须是正定连续对称函数；③无法获得概率式的预测，无法获取预测中的不确定性，同时也不符合实际应用需求；④需要估计折中系数C(回归时需要估计不敏感参数ε)，通常采用交叉验证的方法确定参数的值，这样会增加计算时间，计算复杂度也会随着训练样本数的增加而增加。

Tipping[1-2]提出了一种基于贝叶斯理论的统计学习算法: 相关向量机(Relevance Vector Machine, RVM)，其相对于SVM有以下一些优点：①可以输出预测值的后验概率分布；②比SVM具有更加稀疏的决策函数，即需要相关向量比支持向量更少便可获得与SVM类似的分类准确率;③核函数不需要满足Mercer 条件，可以构造更多的核函数。近年来，在机械故障诊断领域，也有一些RVM的应用与研究成果涌现[3-6]。然而，还未得到相关研究者的足够重视。理论上RVM对于处理小样本问题更具有优势，更加适合处理工程实际问题。同时，RVM相对简单的决策函数所需较少的计算时间更加适合在线诊断。

基于SVM故障诊断模型参数(折中系数C与核函数参数)的设定，很大程度影响着最终的故障诊断准确率。RVM中没有涉及折中参数C，仅需选择合适的核参数值，缓解了参数对其诊断结果的影响。然而，RVM的分类结果对核参数依然十分敏感。传统的方法常采用网格搜索和交叉验证方法相结合以选取最佳的核参数，这种枚举方法消耗了大量的时间和资源。

为此，提出了一种基于RVM的故障诊断模型，利用量子遗传算法(QGA)优化RVM，自适应地选择最优的核函数参数。同时，分别采用遗传算法(GA)和粒子群算法(PSO)优化RVM的核参数，比较分析了不同算法之间的优劣，显示了QGA在核参数优化方面的优势。提取滚动轴承振动信号的EEMD能量作为故障特征，通过优化后的RVM诊断模型进行故障识别。结果表明了所提出方法的可行性和有效性。

1相关向量机分类理论模型

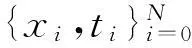
(1)

其中：ω=(w1,w2,…,wN)T为权重的系数向量，Kn(x)为选用的核函数。RVM希望预测出输入样本xi属于某个类别的后验概率，因此可通过Sigmoid函数

(2)

将y(x)映射到(0,1)区间进行分类[1]。

假设每个样本独立同分布，并且每次的预测为独立事件，假设p(t|x)采用Bernoulli分布，可得预测结果t的后验概率的似然函数为

P(t|ω)=

(3)

根据贝叶斯理论的推理过程，为了解决SVM由于过多支持向量造成的过拟合现象，需给定权重ω某个先验概率分布，因此合理的假设权重ω符合Gaussian正态分布，则

(4)

其中：α=(α0,α1,α2,…,αN)为引入控制权重wi的向量，称为超参数；N(·)为正态分布函数。

RVM的核心特点就是引入超参数α对决策函数的权重进行控制，当模型训练结束时，如果超参数很大时，对应权重的值为零，极少数非零权重对应的基函数构成了最终的决策函数，实现了模型的稀疏化[2]。非零权重对应的训练样本的向量称为相关向量。

对于给定的α值，如果已知训练样本的概率分布已知，根据贝叶斯定理可推导出ω的后验概率分布

(5)

其中：p(t|α)为证据函数，p(t|ω)为似然函数。

由于权重P(t|ω)不符合高斯分布，没有解析解，因此采用Laplace逼近方法来近似。又由于

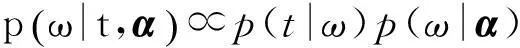
(6)

因此，为了求解在已知α条件下的ω的最可能的权重ωMP，即等价于求

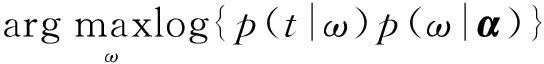
(7)

(8)

其中：yi=σ{y(xi;ω)}，A=diag(α0,α1,α2,…,αN)。

为了求解ωMP，需要对其进行不断的迭代求以取最大值，可采用迭代加权最小二乘方法来求解。在求解过程中，需要首先求得对数后验分布的梯度向量g及Hessian矩阵H，由式(8)微分可得：

g=ωlog{p(t|ω)p(ω|α)}=ΦT(t-y)-Aω(9)

H=ωωlog{p(t|ω)p(ω|α)}=-(ΦTBΦ+A) (10)

其中：B=diag(β1,β2,…,βN)，βn=σ{y(xn)}[1-σ{y(xn)}],Φ称之为设计矩阵，且Φnm=K(xn,xm-1)。

利用Laplace逼近方法中Gaussian正态分布逼近后验概率P(t|ω)，是对后验概率分布的众数位置处函数的二次逼近，此时的后验协方差

Σ′=(-H|ωMP)-1=(ΦTBΦ+A)-1

(11)

对于K(K>2)类多分类问题，似然函数(3)可以表达为

(12)

此时的输出值为多值输出yk(xn;ωk)，每一个输出都有各自独立的权重向量ωk和超参数向量αk。如果直接求解多分类问题时，K类的Hessian矩阵H及Σ′都会非常大，导致计算量也很大，因此可将多分类问题分解成多个二分类问题来解决。

2基于量子遗传算法的核函数参数优化

2.1过程描述

核函数的选择对于最终诊断率有着很大的影响，然而至今也未形成完整的理论解决该问题。在相关的研究中，高斯径向基核函数的表现通常较好。因此，选用高斯径向基核函数作为RVM的基函数。

群智能优化算法被引入到核参数的选择中，利用群智能算法卓越的寻优能力，自适应的选取最优的核函数参数，如GA[7]和PSO[8]。然而GA存在着收敛过慢、易陷入局部最优等缺陷。PSO也存在着易陷入局部最优、局部寻优能力较差等缺点。QGA是在传统GA中引入量子计算的概率和机制形成的新型算法，充分利用量子计算具有天然的并行性，极大地加快了处理信息的速度。与传统GA不同的是，QGA中的染色体用量子比特取代GA中的二进制串，采用量子比特编码，使得一个染色体可以同时表达多个量子态的叠加，即仅通过一个小数量种群的量子个体来代替传统数量较大的个体。此外，量子门操作这一独特的处理步骤，使得QGA拥有良好的全局寻优能力。QGA比GA拥有更好的多样性特征以及更佳的收敛性。因此，采用GA的改进算法QGA自适应地选取最优核参数。图1为QGA优化RVM核参数的流程图。

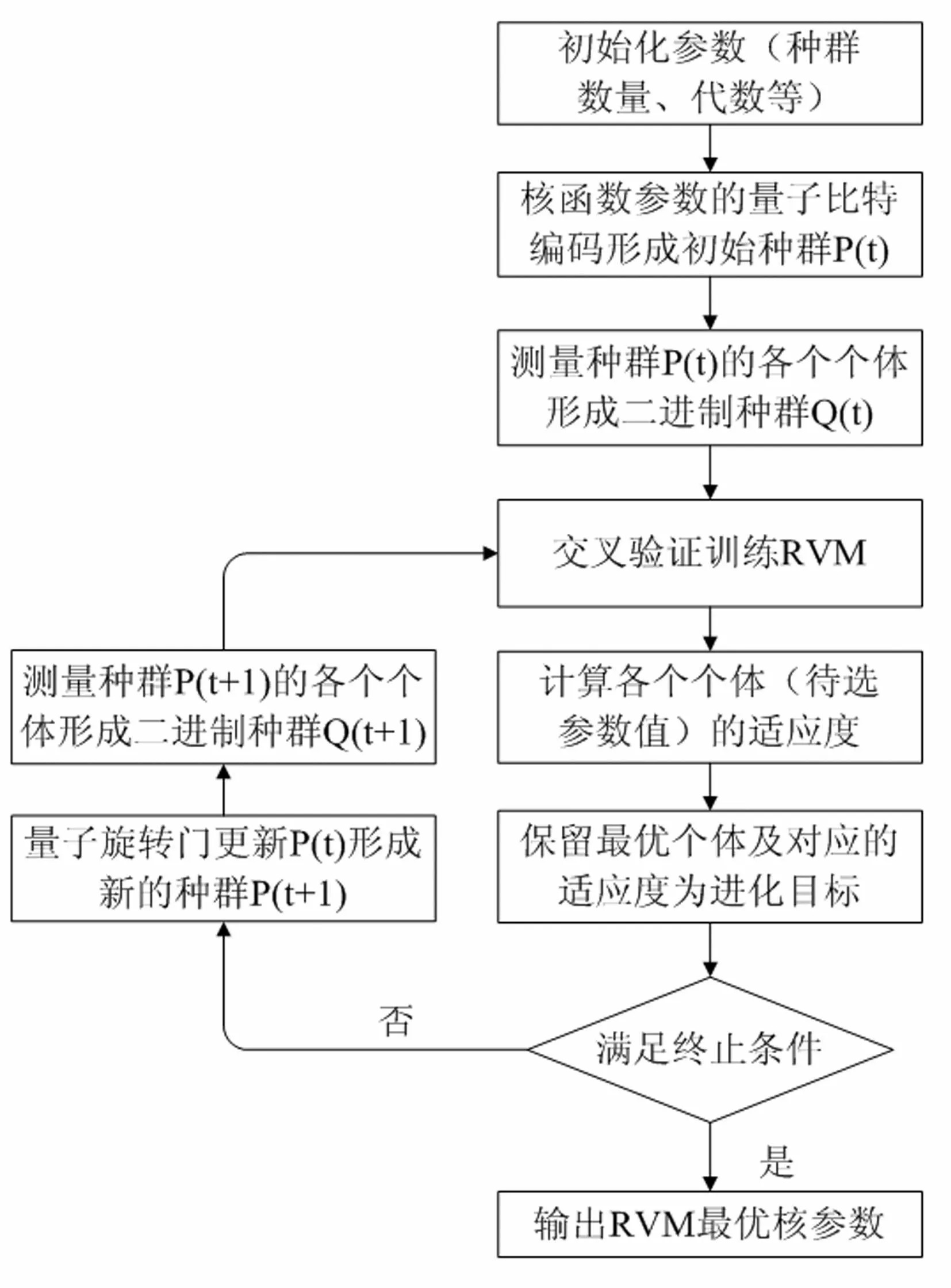
图1　基于QGA优化RVM核参数的流程图 Fig.1 The flow chart of the parameter optimization of RVM based on QGA

具体的核参数优化步骤如下：

步骤1QGA将核参数看做一个染色体。随机产生N条以量子比特为编码的染色体对核参数进行编码，构成初始种群

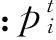
其中一个量子比特表示为|ψ〉=α|0〉+β|1〉，α、β为幅常数，m为一条量子染色体的长度。

步骤2对初始的种群P(0)中的每个个体进行一次二进制的测量，将种群P(0)转化为长度m的二进制串构成的种群Q(0)。

步骤3对种群Q(0)进行适应度评估。对随机产生的待选核参数值的二进制编码转化成十进制，即形成初始的核参数数组，将其每一个核参数值分别代入核函数中，利用RVM对待测数据集进行分类，对适应度(此时为分类准确率)进行评估，保留当前最佳适应度(最佳分类准确率)下的核参数值和对应的适应度，即当前最优个体。

步骤4通过量子门进化操作来更新P(0)获得新的种群P(1)。选择量子旋转门使算法朝着最优解的方向搜索，此时

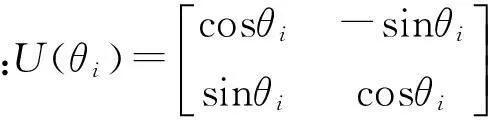
步骤5令t=t+1,并返回步骤2。以此不断迭代更新，最终获取最优的RVM核函数参数。

2.2关键参数的设置

在利用QGA自适应地获取最优RVM核函数参数之前，需要对优化算法中的一些关键的参数进行初始化设置，主要包括以下参数的设置：

初始化种群。P(0)中各个(α,β)均初始化为(1/sqrt(2),1/sqrt(2))，表示在初始进化时一个染色体所有状态均以相同的概率进行叠加。

适应度函数Fitness。采用QGA优化RVM的目的是为了获得最优的分类准确率。因此，选取分类的准确率作为QGA优化核函数参数中的适应度函数，即

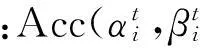
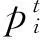
算法的结束条件。当最大的迭代数超过初始的设置代数或当连续10代的最佳适应度(分类准确率)之差的绝对值小于0.001，此时核参数的优化程序终止。

2.3仿真分析

为了验证QGA在RVM核参数优化中的有效性，采用高斯径向基函数作为核函数，选取UCI标准数据库中的Wine、Iris以及Cancer三个标准数据集作为实验数据，分别采用QGA、GA和PSO选取RVM对实验数据进行分类时的最优核参数。仿真实验在CPU速度为3.30 GHz，内存为4 GB的计算机下进行，基于Matlab平台，对比研究了QGA优化RVM(QGA-RVM)、GA优化RVM(GA-RVM)以及PSO优RVM(PSO-RVM)三种方法之间选取最优核参数方面的性能，以此来分析QGA在核参数优化中的优越性。表1为UCI数据库中4种测试数据的样本个数、样本维数及类数的说明。

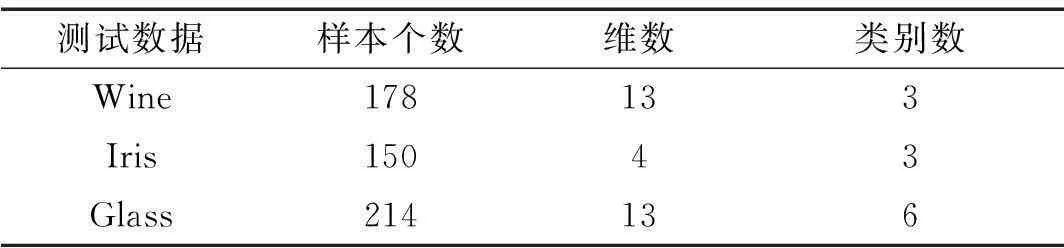
表1　测试数据集说明

表2显示了不同种方法优化RVM后对UCI标准数据库3种数据进行50次分类实验后的平均分类准确率以及平均运行时间。从表2中的结果可见，对于Wine、Iris、Glass三种测试数据集，三种不同算法优化后的RVM分类的准确率效果相差不大。相比较而言，QGA-RVM的平均分类准确率最高，GA-RVM和PSO-RVM对不同数据的测试结果互有高低。此结果说明了QGA算法在测试过程中每次都能自适应的选取到最佳的核函数参数，而GA和PSO算法在测试过程中出现了核函数参数值陷入局部最优、早熟收敛等问题，未收敛到最优的核参数值。从测试的时间上看，QGA-RVM的平均运行时间最低，体现了QGA算法在优化RVM过程中并行计算的优势。

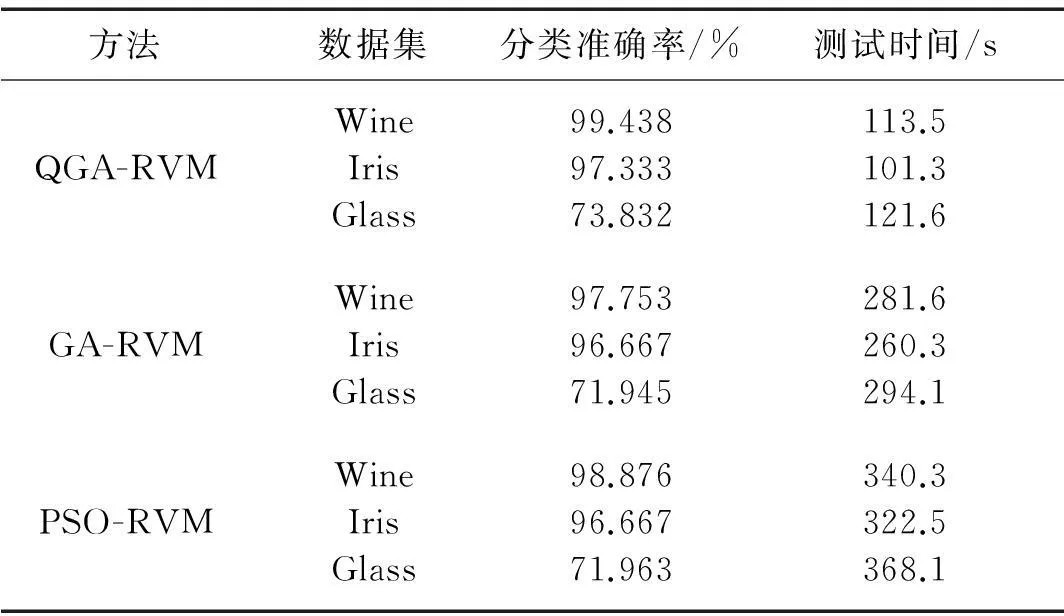
表2　不同算法对测试数据分类结果

3滚动轴承故障诊断实例分析

3.1实验数据

滚动轴承故障试验的数据来自于美国Case Western Reserve University轴承数据中心。试验采用的轴承型号为6205-2RS JEM SKF深沟球轴承，采样频率fs=12 000 Hz，轴承的转速为1 748 r/min。实验中分别获取不同载荷 (0 ph,1 ph,3 ph)、不同故障程度下三种轴承故障的振动测试数据以及正常轴承数据。三种故障分别为外圈点蚀故障、内圈点蚀故障及滚动体点蚀故障。其中点蚀故障通过电火花加工生成，其故障程度为0.178～1.016cm。

3.2故障特征提取

EEMD(Ensemble Empirical Mode Decomposition)是一种基于EMD(Empirical Mode Decomposition，经验模态分解)的改进的信号自适应分解方法，通过对待分解信号加入白噪声后再进行多次分解求平均，有效地减少了EMD分解中的模态混淆现象[10]。EEMD作为一种非线性、非平稳信号有效的时频分析方法，近年来，在旋转机械故障诊断中得到了有效应用[11-12]。原始的复杂信号可以被EEMD自适应的分解为多个内禀模态函数(IMF)之和，不同的IMF分量包含着不同的频率信息成分。不同的机械故障发生时，振动信号中就会产生不同的频率成分，不同频带上振动信号的能量就会不同，即各个IMF上的能量分布不同[13]。因此，提取滚动轴承经EEMD分解后的IMF能量作为故障特征。

设加入了白噪声后的待分解滚动轴承振动信号为

xi(t)=x(t)+ni(t)

(13)

其中：x(t)为原始信号，ni(t)为第i次加入的白噪声，i=1,2,…,M。其中M为初始的平均次数。

用原始的EMD算法将xi(t)自适应分解为若干个IMF之和，即

(14)

其中：n=1,2,…,N，N为分解后IMF的个数，ci,n(t)为第i次加入白噪声后分解得到的IMF分量，ri,N(t)为本次分解后剩余的残差。

通过添加不同的白噪声，重复上述两个步骤M次后得到每次分解后IMF分量的集合为

[{c1,n(t)},c2,n(t),…,cM,n(t)]

(15)

对每次分解后的IMF分量进行总体平均运算来消除白噪声对实际IMF的影响，得到最终的IMF

(16)

其中：cn(t)为EEMD分解后的第n个IMF。

滚动轴承振动信号x(t)经过EEMD最终分解为

(17)

其中：r(t)为最终的剩余残差。

EEMD分解滚动轴承振动信号形成的第n个IMF的能量可以表达为

(18)

假设r(t)忽略不计，信号整体的能量值E应该等于IMF的能量之和，即

E=E1+E2+…+EN

(19)

能量值通常较大，为了便于故障诊断模型的最终诊断，对Ei进行归一化处理后构建故障的特征向量

T=[P1,P2,…,PN]

(20)

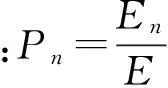
3.3效果分析

选择载荷3 ph、故障程度为1.63cm的实验数据为本研究的分析数据。每个样本由2 048个连续采样数据构成，每种滚动轴承状态下有59个样本。每种状态下任意选取20个样本作为RVM诊断模型的训练样本(共80个)，剩余的样本(共156个)构成模型的测试样本。

对滚动轴承4种状态下的振动测试信号进行EEMD分解，根据上述故障特征提取的步骤，分别提取4种状态下的IMF能量作为滚动轴承的故障特征。以外圈故障信号为例，设置M=100，白噪声的幅值为0.2。图2显示了EEMD分解过程。见图2，外圈故障信号的一个样本被分解成为11个IMF:c1(t)，c2(t)，…，c11(t)和一个残差r(t)。

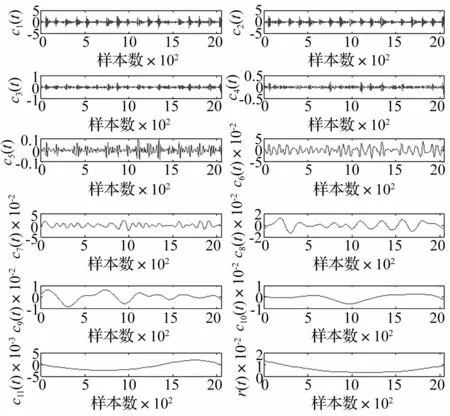
图2　外圈故障信号EEMD分解图 Fig.2 EEMD decomposition results of outer race fault signals

经过分析，提取前6个IMF的能量即可反映出各种状态下能量的差别，以此构成诊断模型的输入特征向量。提取的IMF能量被分成训练样本和测试样本。图3显示了滚动轴承4种状态下的IMF能量分布图。

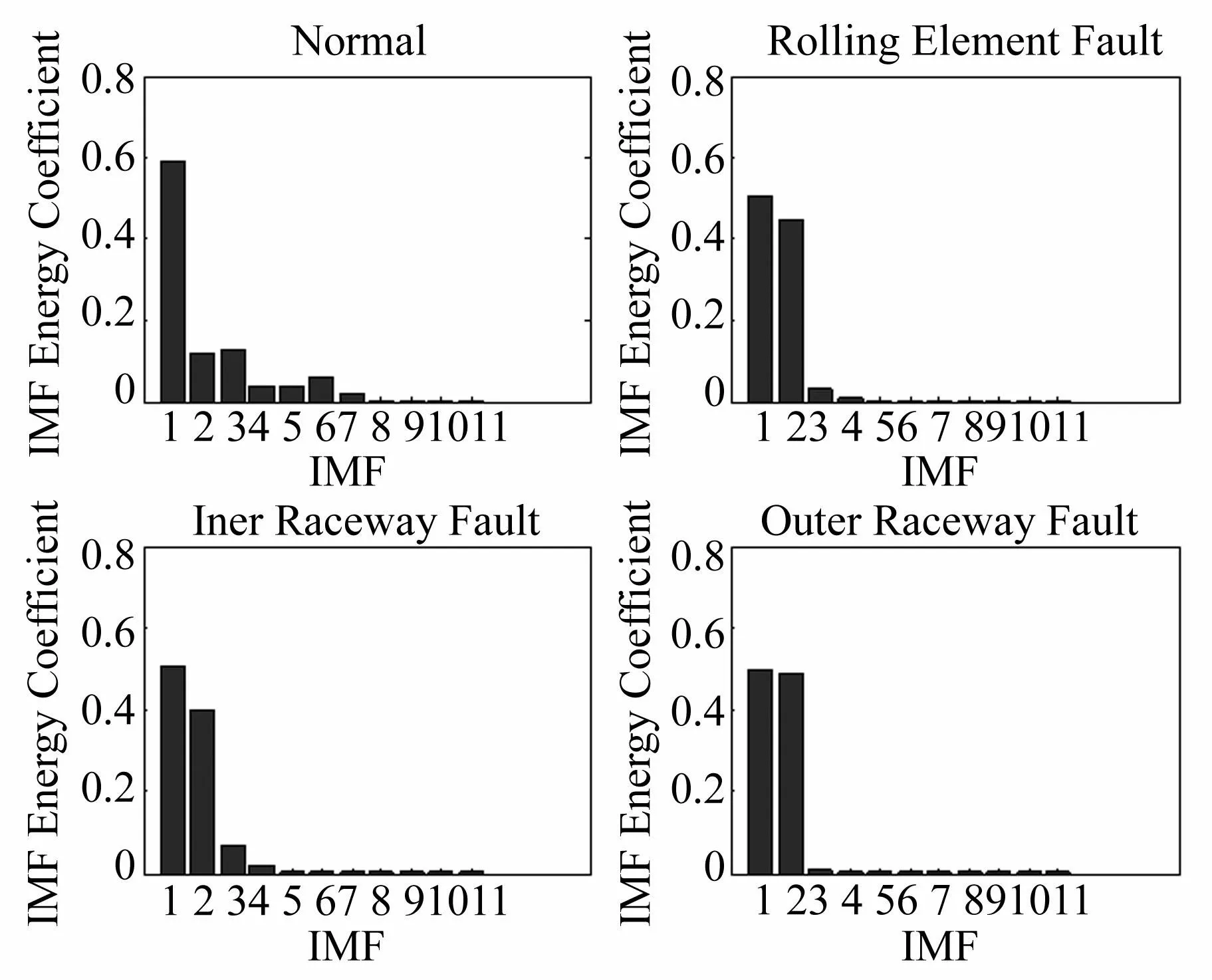
图3　不同状态下EEMD能量分布图 Fig.3 EEMD energy spectrum of different conditions

对于4种滚动轴承状态智能诊断的多分类问题，采用“一对一”策略，构建6个RVM二类故障诊断器进行诊断。将训练样本分别输入到QGA-RVM中，选用高斯径向基核，利用QGA算法自适应的选取各自最优的核参数σ。将测试样本分别输入到各自训练好的QGA-RVM中，最终智能的输出诊断结果。为了验证所提诊断模型的有效性和稳定性，以10次故障诊断实验后的平均故障诊断率作为评价指标，同时将滚动轴承的IMF能量输入到RVM、 SVM以及QGA优化的SVM(QGA-SVM)中做对比分析研究。其中各个模型均采用高斯径向基核函数，由于RVM及SVM没有采用优化算法，其核参数人为设置，最终的诊断实验结果见表3。

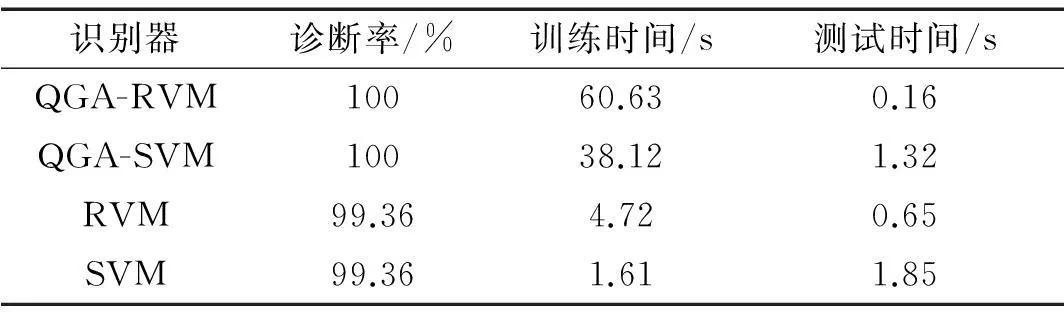
表3　不同种诊断模型的故障诊断实验结果

从表3中的结果可见，QGA-RVM诊断模型及QGA-SVM诊断模型的平均诊断率最高，达到100%，说明基于QGA的核参数选择方法在RVM和SVM的核参数优化中均达到了最优值。而其它两种诊断模型的平均诊断率相对较低，但也基本上能够识别出主要故障，其主要原因是由于人为设置了核参数的值，未设置成最优值。表3中同时也显示了各个诊断模型的训练时间和测试时间。QGA-RVM、QGA-SVM和RVM的平均训练时间比SVM的平均训练时间要长，其中QGA-RVM的时间最长。由于RVM在分类训练过程中需要不断的迭代，影响了其训练的效率。而QGA优化RVM的过程需要再次的迭代，因而再次增加了模型的训练时间。但实际的故障诊断中，诊断模型都是在诊断之前已经训练完成，因此不影响整体故障诊断过程的效率。对于诊断模型的测试时间，QGA-RVM的测试时间最少，RVM次之，QGA-SVM和SVM的测试时间最长。这是由于RVM需要的相关向量比SVM支持向量更少，即RVM的决策函数更加稀疏。虽然QGA-RVM和QGA-SVM都能准确的诊断出故障，但QGA-RVM的测试时间更短。因此，基于以上分析，RVM更加适合处理小样本问题，同时更加适合应用于在线故障诊断。

4结论

提出了一种基于QGA优化RVM核函数参数的方法，利用了QGA具有全局搜索寻优能力强、种群多样性、收敛速度快及并行计算时间短等特点，自适应地选取最优核参数，并将其应用于滚动轴承的智能故障诊断中。通过仿真，将GQA优化的RVM与PSO以及GA优化的RVM进行数据分类实验对比，利用UCI 标准数据集中的三个数据作为被测数据，结果表明了QGA在核函数参数寻优方面的优势。利用EEMD将滚动轴承的故障信号自适应的分解成若干个IMF，提取各个IMF能量作为故障特征，并将其输入到QGA-RVM进行最终的故障诊断。结果表明，该方法能够快速、准确地诊断出滚动轴承的故障；同时，将EEMD能量特征输入到SVM中进行对比研究，同样也显示了RVM在故智能故障诊断中的优越性。

参考文献

[1]Tipping M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001,1(3):211-244.

[2]Tipping M E. Bayesian inference: An introduction to principles and practice in machine learning[J]. Advanced Lectures on Machine Learning, 2004,3176:41-62.

[3]周晓英, 李巍华, 丁康. 基于关联向量机的齿轮故障检测方法研究[J]. 振动与冲击, 2008,27(6):51-54.

ZHOU Xiao-ying, LI Wei-hua, DING Kang. Gear fault detection based on relevance vector machine[J]. Journal of Vibration and Shock, 2008,27(6):51-54.

[4]Widodo A, Yang B S, Kim E Y, et al. Fault diagnosis of low speed bearing based on acoustic emission signal and multi-class relevance vector machine[J]. Nondestructive Testing and Evaluation, 2009,24(4):313-328.

[5]Li N, Liu C, He C, et al. Gear fault detection based on adaptive wavelet packet feature extraction and relevance vector machine[J].Proceedings of the Institution of Mechanical Engineers part C-Journal of Mechanical Engineering Science, 2011,225(C11):2727-2738.

[6]He C, Liu C, Li Y, et al. Intelligent fault diagnosis of rotating machinery based on multiple relevance vector machines with variance radial basis function kernel[J]. Proceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science, 2011,225(C7):1718-1729.

[7]董超, 田联房, 赵慧洁. 遗传关联向量机高光谱影像分类[J]. 上海交通大学学报, 2011(10):1516-1520.

DONG Chao,TIAN Lian-fang, ZHAO Hui-jie. Hyperspectral image classification by genetic relevance vector machine[J]. Journal of Shanghai Jiaotong University, 2011(10):1516-1520.

[8]Du W L, Li A S, Ye P F, et al. Fault diagnosis of plunger pump in truck crane based on relevance vector machine with particle swarm optimization algorithm[J]. Shock and Vibration, 2013,20(4):781-792.

[9]杨俊安, 庄镇泉, 史亮. 多宇宙并行量子遗传算法[J]. 电子学报, 2004(6):923-928.

YANG Jun-an, ZHUANG Zhen-quan, SHI Liang. Multi-universe parallel quantum genetic algorithm[J]. Acta Electronica Sinica, 2004(6):923-928.

[10]Wu Z, Guang N E. Ensemble empirical mode decomposition: A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009,1(1):1-41.

[11]沈长青, 谢伟达, 朱忠奎, 等. 基于EEMD和改进的形态滤波方法的轴承故障诊断研究[J]. 振动与冲击, 2013,32(2):39-43.

SHEN Chang-qing, Peter W.Tse, ZHU Zhong-kui, et al. Rolling element bearing fault diagnosis based on EEMD and improved morphological filtering method[J]. Journal of Vibration and Shock, 2013,32(2):39-43.

[12]周智, 朱永生, 张优云, 等. 基于EEMD和共振解调的滚动轴承自适应故障诊断[J]. 振动与冲击, 2013,32(2):76-80.

ZHOU Zhi, ZHU Yong-sheng, ZHANG You-yun, et al. Adaptive fault diagnosis of rolling bearings based on EEMD and demodulated resonance[J]. Journal of Vibration and Shock, 2013,32(2):76-80.

[13]Yu Y, Yu D J, Cheng J S. A roller bearing fault diagnosis method based on EMD energy entropy and ANN[J]. Journal of Sound and Vibration, 2006,294(1-2):269-277.