舰船全船冲击环境数值预报方法研究

第一作者崔杰男，博士，讲师，1984年3月生

舰船全船冲击环境数值预报方法研究

崔杰1，李烨2，陈莹玉2，周塞北1，宋红宝2

(1.江苏科技大学船舶与海洋工程学院，江苏镇江212003; 2.哈尔滨工程大学船舶工程学院，哈尔滨150001)

摘要：借助数值仿真的手段，采用通用有限元软件ABAQUS建立水下爆炸声固耦合方法，模拟水下非接触爆炸作用下舰船冲击响应特性，并通过实船实验数据进行对比，该方法可较好地模拟水下爆炸舰船的冲击环境。在此基础上，计算水下爆炸作用下全船纵向冲击谱值分布规律，总结并拟合出具备一定通用性的数学模型，可用于冲击环境的初步预报。同时得到了全船冲击环境沿垂向位置的分布情况，以及冲击环境随不同攻角条件下的变化规律，为舰船结构的抗冲击设计提供参考。

关键词：冲击环境；水下爆炸；数学模型；声固耦合

基金项目：国家自然科学基金青年基金项目(51409129,U1430236);江苏省自然科学基金青年基金项目(BK20140504)

收稿日期：2015-02-02修改稿收到日期：2015-03-29

中图分类号:N913T31;T1.47

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.17.015

Abstract:Here, numerical simulation and acoustic-structure coupling methods based on ABAQUS were used to simulate the dynamic response of a hull subjected to non-contact underwater explosion. Comparing the simulation data with experimental ones, it was shown that the proposed methods can simulate and predict better the shock environment of warships under the action of underwater explosion. Furthermore, the longitudinal shock spectra distribution laws of the hull under the action of underwater explosion were computed and the mathematical models with some level of generality were established to predict the shock environment. The vertical distribution laws of the hull’s shock environment and its change laws under conditions of different attack angles were obtained. The study results provided a reference for shock-resistant design of warships.

Numerical prediction methods for shock environmental of ship’s entire hull

CUIJie1,LIYe2,CHENYing-yu2,ZHOUSai-bei1,SONGHong-bao2(1. School of Naval Architecture and Offshore Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China;2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)

Key words:shock environment; underwater explosion; mathematical models; acoustic-structure coupling

大型水面舰船作为我国舰船发展的必然趋势，其战斗力和生命力越来越受到重视和关注，而且与战斗力和生命力直接相关的是舰船的抗爆抗冲击性能，因此随着我国海军的逐步发展，提高舰船的抗爆抗冲击性能显得越来越重要[1-3]。

舰船在实战状态下的冲击环境受到多方面因素的制约，包括攻角，爆点位置，冲击因子等，各因素之间的关系错综复杂。就目前所公开的冲击环境预报方法并不多，而且大多仅仅在单个因素下讨论冲击环境规律。冯麟涵等[4]基于特征谱速度和冲击环境本征方程提出了一种舰船冲击环境的工程化预报方法，该方法考虑了外载荷参数，舰船尺度特征以及系统固有特征，具备很强的通用性，为舰船的早期设计阶段开展抗冲击设计提供良好参考，但预报过程过度注重设备，因而导致计算量较大以及很难在早期预报中拥有对舰船冲击环境状况的全局性的把握。Keil[5]根据船型、装置类型及入射角等总结了冲击环境估算公式，但部分系数的可靠性需要结合实船试验才能最终确定。古滨等[2]基于样本库的方法对舰船的冲击环境进行预报，比较全面地总结了冲击环境与船长、型深、冲击因子以及排水量之间的关系，较为完善地提供了不同吨位舰船的冲击环境样本库，但样本库中的样本分布较为稀疏，而且仅仅针对小冲击因子，对于冲击因子0.6以上的情况则未给出详细介绍，同时也并未提供具体规律对应的数学模型。因此，本文在总结目前的研究现状的基础上，通过对典型舰船的数值仿真计算，从对舰船整体把握的角度出发，总结出远场爆炸作用下冲击环境的具体衰减规律的数学模型，并进行了精度验证。同时进一步完善了远场水下爆炸舰船冲击环境的规律与外界影响参数之间的关系。

1冲击载荷模型

根据水下爆炸理论，作为高能材料的炸药在水下爆炸后会立即产生高温高压气体，并推动周围的水域形成峰值极高的冲击波，但在传播过程中压力会迅速衰减[6]。而其后产生的气泡脉动则具备很宽的脉宽，虽然峰值不及冲击波的20%，但其中具备的能量和比冲量却足以和冲击波接近。

对于遭受中远场水下爆炸载荷冲击的水面舰船而言，气泡脉动对舰船结构的影响同样不能忽略，关于计及气泡脉动的水下爆炸载荷，Geers和Hunter在2002年前后给出了较好的水下爆炸载荷的半经验公式[7-9]。但该系列公式建立在如下假设之上：第一，水下爆炸冲击波产生过后的压力的理论结果的得到均视流体为无粘无旋且不可压缩的流体，即忽略外界压力变化对水的密度的影响；第二，载荷推导的过程均将气泡的运动视为球形运动，不考虑非球形效应对计算的影响。以TNT炸药为例，基于以上假设的气泡载荷压力表达式如下：

pI(xj,t)=pt(t)px(xj)

(1)

在t<7Tc时(冲击波阶段)，冲击波压力：

(2)

在t>7Tc时(气泡脉动阶段)，气泡脉动压力：

(3)

根据水下非接触爆炸载荷的基本特点以及G-H模型结合自编程序得到冲击波以及气泡脉动载荷[10]。通过在INP文件中定义载荷的加载方式将冲击波和气泡脉动载荷加载到船体结构上，采用声固耦合法计算水下爆炸作用下舰船的冲击环境。

2数值方法有效性验证

舰船水下爆炸数值计算方法的有效性直接影响到计算结果对应的工程参考价值，因此有必要将基于声固耦合的舰船冲击环境数值结果与实船实验结果进行对比。本文建立某型舰船有限元模型，利用声固耦合法进行水下爆炸数值模拟。从船艏到船艉的选取7个典型的位置，将冲击环境的谱加速度值(单位：g)的实船实验结果和数值计算结果进行对比，对比数据如图1柱状图所示，其中每个测点对应的左侧柱状图代表测量值，右侧代表计算值，并在图中标明对应测点的谱加速度误差。

从图1所示实船和数值模拟数据的对比分析可以发现，数值计算与实船试验之间的平均误差为17.15%，控制在30%以内，具有较好的精度，能比较合理地反映舰船结构在水下爆炸中的冲击响应。

图1　测点谱加速度值对比 Fig.1 Comparison of the acceleration spectrum in measure point

3有限元模型及工况设置

本文选取某大型舰船作为研究对象，运用有限元软件ANSYS按照1∶1的比例进行三维实体建模，舰体结构主要采用壳单元和梁单元，壳单元类型为S4R，计算方法为四节点减缩积分，梁单元类型为B31(3节点梁单元)，网格平均大小为0.25m。对于船用设备，在计算时将其简化的MASS质量点或质量块单元，以保证整船的重量分布。外部流场单元类型为AC3D4的声学单元，考虑到舰船受到阻尼和惯性等方面的影响，所建流场半径与结构半径之比为6[11]，在减少计算量的情况下尽可能地减少系统增加的附加质量率，以保证计算精度。舰船与流场耦合示意图见图2。

图2　有限元模型与流场耦合示意图 Fig.2 Sketch of finite element model of ship coupling with fluid

对于舰船材料，主要使用舰船用945钢。国际上常用材料的本构方程主要包括：Johnson-Cook(简称JC模型)和Cowper-Symonds(简称CS模型)两种模型。但CS 模型仅考虑应变率效应，将材料屈服应力的动态值与静态值的比作为应变率的函数，参数较少，使用方便。因此本研究在软件中采用PLASTIC-KINEMATIC模式，采用Cowper-Symonds模型考虑应变率影响，应变率影响系数为：

(4)

对于工况设置，选取装药量为1 000 kgTNT，爆炸距离为0.16L(L为船长)，选取爆点为L/4、L/2、3L/4三个典型位置，爆点设置见图3，详细工况见表1。其中，攻角定义为爆点与参考点的连线与水平面之间的夹角。为了方便分析全船冲击环境在各工况中的分布规律，所有数值结果采用无量纲的形式，其中无量纲谱速度以工况2中0.3L处对应谱速度为标准量，无量纲船长和无量纲型深分别以水线间长及型深为标准量进行无量纲化。

图3　各爆点位置示意图 Fig.3 Sketch of explode location

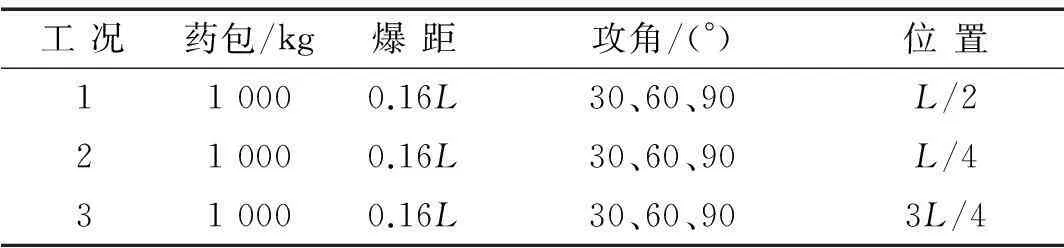
工况药包/kg爆距攻角/(°)位置110000.16L30、60、90L/2210000.16L30、60、90L/4310000.16L30、60、903L/4

4计算结果分析

4.1相同甲板不同爆点的冲击环境规律

相对于横向和纵向水下爆炸冲击响应主要以垂向为主，本文进行冲击环境分析时均着重研究垂向响应[12-14]。由于船体各甲板中一甲板、二甲板和三甲板的长度最长，与型长最为接近，可以最大程度地体现谱速度沿船长方向上的分布规律，所以在研究冲击环境随爆点变化的规律时选取舰船的一、二、三甲板作为研究对象。各甲板上的考核点无量纲谱速度值沿船长方向的分布以及对应的数值拟合曲线见图4～6。其中各曲线横坐标数值表示距船首的距离，各考核点均在中纵剖面上。

图4　3甲板纵向谱速度及拟合分布曲线 Fig.4 Longitudinal distribution of spectrum velocity and fitted curve in deck 3

图5　2甲板纵向谱速度及拟合分布曲线 Fig.5 Longitudinal distribution of spectrum velocity and fitted curve in deck 2

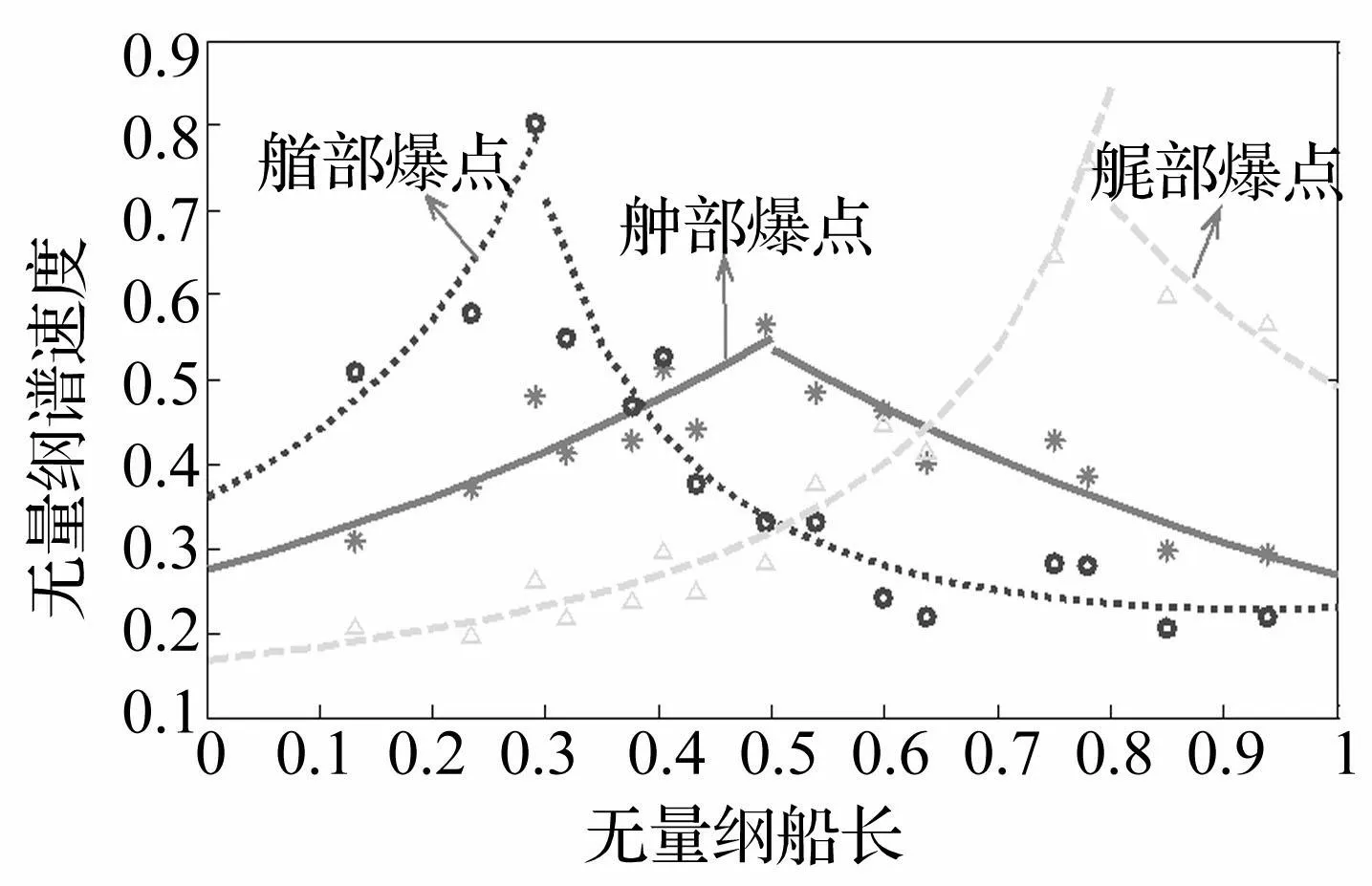
图6　1甲板纵向谱速度及拟合分布曲线 Fig.6 Longitudinal distribution of spectrum velocity and fitted curve in deck 1

将图4～6中各工况计算数据进行拟合，根据拟合结果可知，多项式模型对于散点的拟合效果最好，其次是倒数模型和Bleasdale模型。考虑到多项式过于复杂并且缺乏规律可循，而倒数模型和多项式的拟合精度十分接近，考虑到精度和计算量等多方面因素，因此选用上述倒数模型及Bleasdale模型对冲击谱速度进行前期预报是较为合适的。

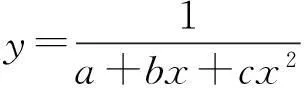
表2　各工况拟合曲线数学模型及参数范围

基于以上数值计算，对本文所总结的特定冲击因子范围内的远场水下爆炸谱速度预报公式的精度和有效性进行验证十分必要。同时考虑到大型水面舰船的远场实船爆炸冲击环境数据的匮乏以及文献[4]提出的预报公式具备较强的通用型，因此本文选取爆点在船舯位置时典型甲板位置处谱速度数值计算结果同文献[4]进行对比[15-16]，其对比数据如表3所示。从表3可以发现，上述4.1小节所总结的数学模型对谱速度的预报与文献[4]的结果较为接近，误差基本控制在30%以内，具备一定的工程预报精度，可用于特定冲击因子条件下大型水面舰船冲击环境前期预报及为抗冲击设计提供一定的参考。

表3　甲板典型位置谱速度预报

4.2相同冲击位置下沿甲板垂向冲击环境规律

4.2.1典型甲板高度的垂向冲击环境规律分析

为了体现舰船冲击环境在不同甲板间的变化情况，图7～8给L/4和3L/4处爆炸工况下舰船各层甲板测点的无量纲谱速度纵向分布曲线。由图7～8可知，爆点位于船艏L/4时，各层甲板整体趋势为爆点正上方L/4处谱速度最大，沿着船长方向向船体艏艉呈衰减趋势。同时船艉部分节点的谱速度有回弹的趋势，可能是船艉处的结构相对比较薄弱刚度变化剧烈从而局部运动幅值较大所引起的。由于爆点位于船底，距离爆点最近的3甲板的谱速度最大，而相对爆点较远的1甲板谱速度则较小，且各曲线峰值基本在爆点0.25L或0.75L附近，符合船体冲击环境响应的纵向和垂向规律。船艉冲击(3L/4)时也存在类似的规律。

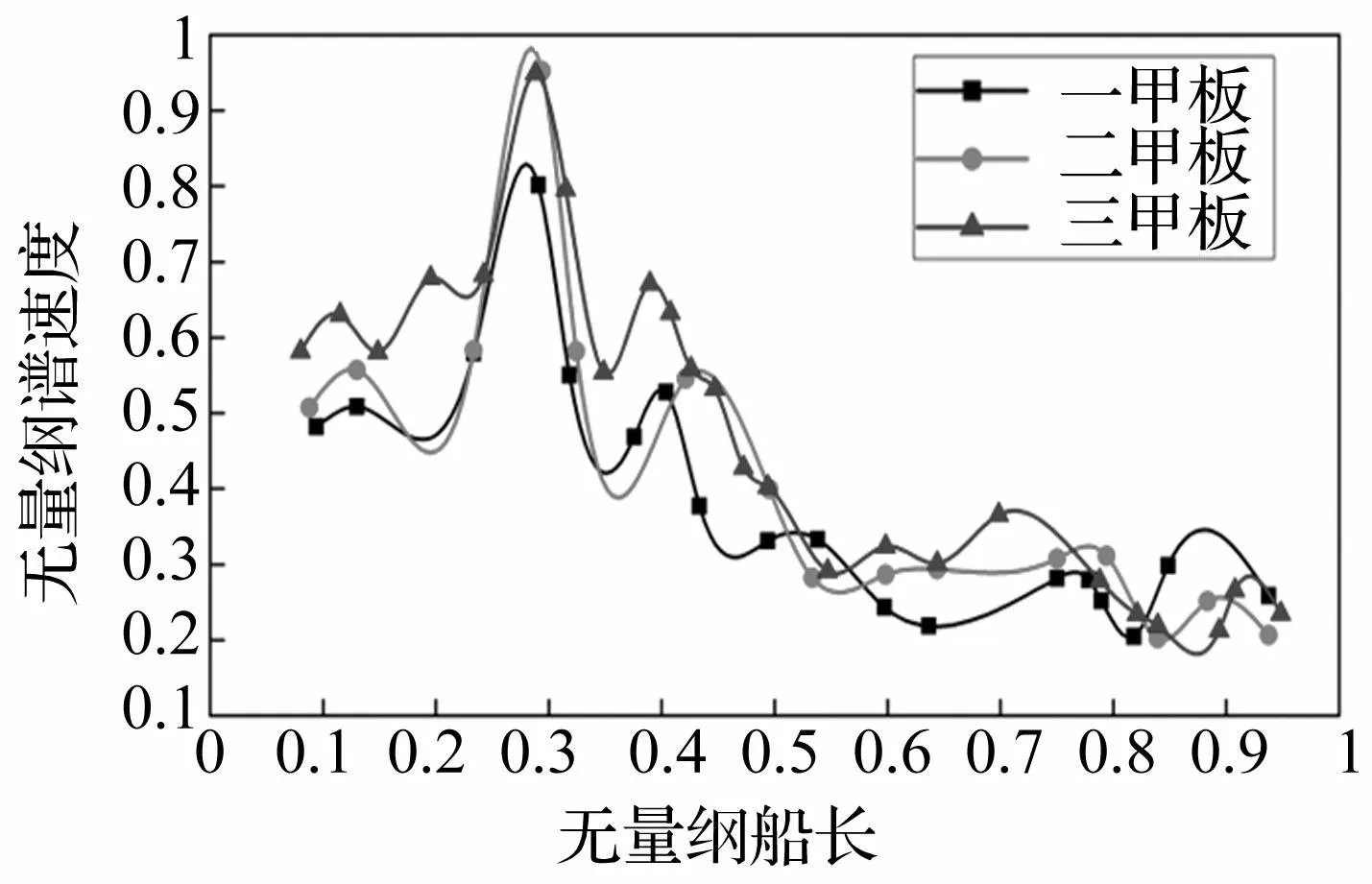
图7　首部冲击下各甲板谱速度分布曲线(L/4) Fig.7 Distribution curves of non-dimensional spectrum velocity in each deck for the L/4 condition

图8　尾部冲击下各甲板谱速度分布曲线(3L/4) Fig.8 Distribution curves of non-dimensional spectrum velocity in each deck for the 3L/4 condition

4.2.2典型舱壁的垂向冲击环境规律分析

船体的冲击响应在甲板之间仅能归纳出间断性的粗略定性衰减规律，为了获得更为连续的垂向冲击响应的衰减情况，本小节设置了一系列典型舱壁结构上垂向测点，以型深作为变量，以期获取舱壁节点随着远离基点的衰减规律。舱壁位置以无量纲形式表示，选取典型舱壁位置分别在0.43L～0.7L之间，基本涵盖船体爆点的主体影响区域。舱壁位置及测点在舱壁上的分布见图9和图10，图10中所有测点(X1，X2…Xn)均在中纵剖面和舱壁板的交线上。

图11表示各个典型舱壁结构上的测点的谱速度随着型深变化的分布曲线，其中型深的基点位于船体基线上。由上图可知，各个横剖面随着测点位置的升高有着相似的衰减规律。通过对曲线进行的数值拟合分析可以发现，其数值基本按照指数规律衰减，且衰减的数学模型为y=a(b-e-cx)。此外从图中可见距离爆点最近的0.51L剖面谱速度整体依然最大，同样与船体纵向分布规律相吻合。因此可认为远场水下爆炸载荷下的冲击响应在铅垂方向上满足指数衰减规律。

图9　典型舱壁纵向位置 Fig.9 Longitudinal locations of typical transverse bulkheads

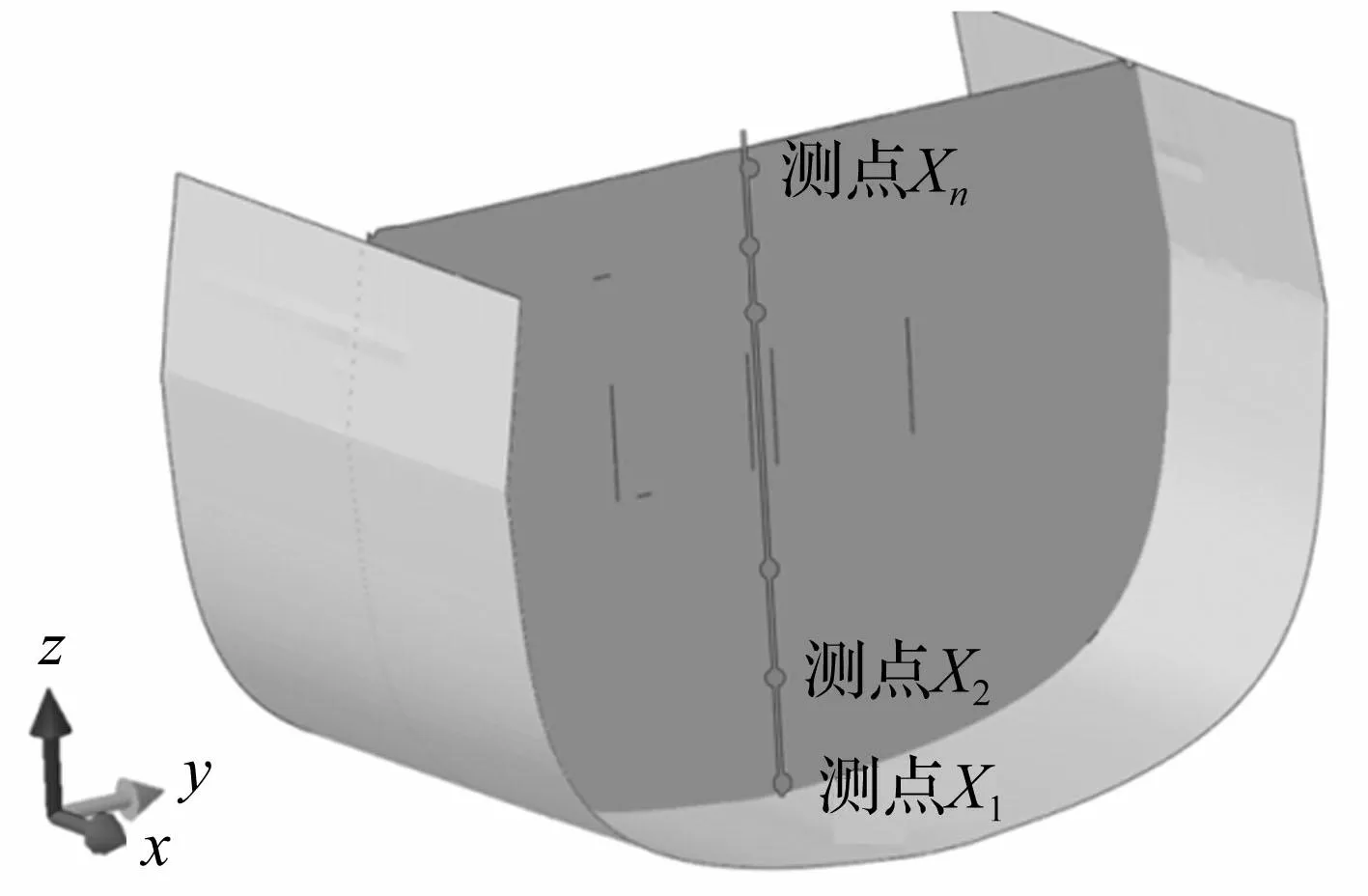
图10　测点在舱壁上的分布 Fig.10 Location of stations in transverse bulkhead

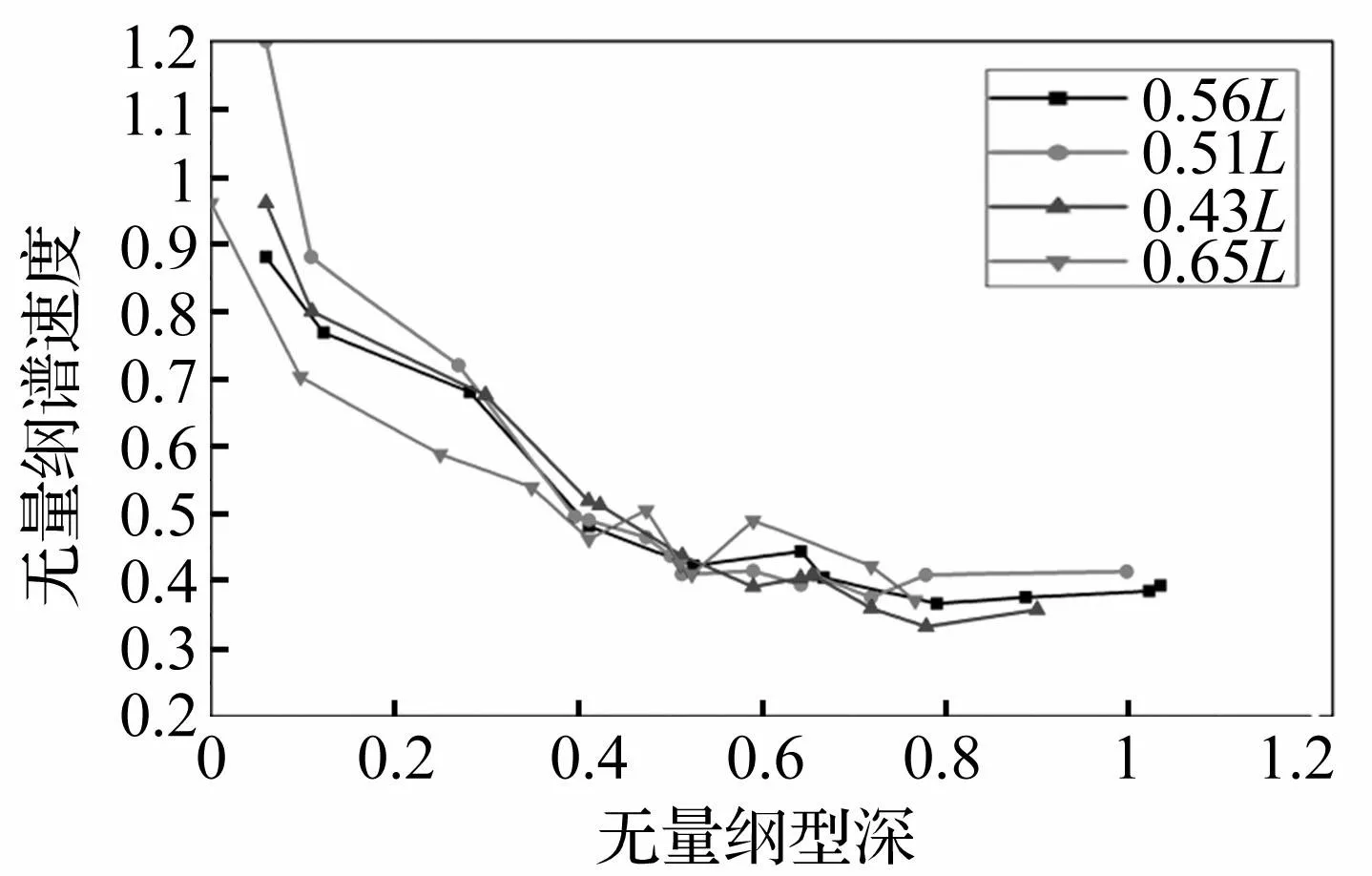
图11　典型剖面上垂向冲击环境分布曲线 Fig.11 Distribution curves ofvertical non-dimensional spectrum velocity in typical sections

4.2.3相同甲板攻角变化下的冲击环境规律

为了分析攻角变化对舰船冲击环境规律的影响，选取3甲板作为典型分析对象。爆炸冲击位置在艏部L/4处和艉部3L/4处，攻角分别于30°，60°，90°。相应曲线见图12～图15。由图12和图14可见，谱速度随攻角增加而增大，其中30°响应最小，90°响应最大。对典型纵向位置不同攻角的谱速度值进行拟合，见图13和图15，谱速度大小随攻角的变化基本呈线性关系。对于非爆炸位置的船体结构而言，攻角从0°到90°变化时，舰船受冲击后的响应没有产生特别大的区别，斜率较平缓；在船体的爆点附近数据变化较明显，且爆点位置所在剖面的直线斜率较大，可见攻角对于爆点附近谱值的影响比较明显。

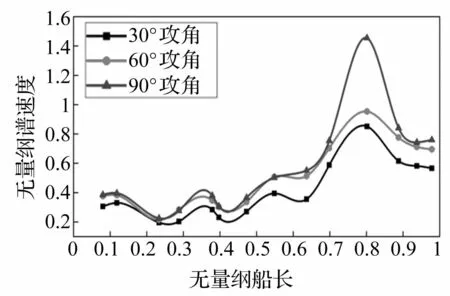
图12　不同攻角谱速度分布曲线(3L/4) Fig.12 Distribution curves of non-dimensional spectrum velocity in each attack angles for the 3L/4 condition

图13　典型剖面谱速度随攻角变化规律(3L/4) Fig.13 Variation trend of non-dimensional spectrum velocity with attack angles in typical sections for 3L/4 condition

图14　不同攻角谱速度分布曲线(L/4) Fig.14 Distribution curves of non-dimensional spectrum velocity in each attack angles for the L/4 condition

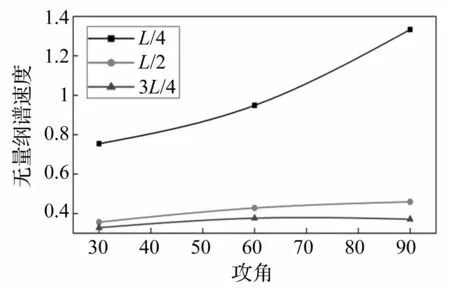
图15　典型剖面位置谱速度随攻角变化规律(L/4) Fig.15 Variation trend of non-dimensional spectrum velocity with attack angles in typical sections for L/4 condition

5结论

本文通过对典型舰船设置不同水下非接触爆炸工况，采用声固耦合法数值模拟水下非接触爆炸作用下舰船的运动响应，分析和总结全船冲击环境的特点及规律，得出以下结论：

(1)通过对各甲板纵向谱速度数值模拟结果的分布规律研究，利用数值拟合的方法得到各典型工况下舰船全船冲击环境对应的数学模型，其谱速度纵向分布满足以爆点为中心的倒数、幂函数和对称衰减规律；

(2)通过对典型舱壁板上垂向分布的测点的谱值变化规律进行拟合分析，得到各个横剖面随着测点位置的升高呈指数规律衰减的规律；

(3)谱速度随着攻角和冲击因子的增大而不断增大，且二者之间近似呈线性关系变化，且上述影响因素在爆点附近对船体响应的影响更为明显。

参考文献

[1]许维军，姚熊亮，梁德利.水下爆炸冲击载荷作用下潜艇冲击环境仿真研究[J]. 哈尔滨工程大学学报,2006, 27(3):372-376.

XU Wei-jun, YAO Xiong-liang, LIANG De-li. Research on simulation of underwater shock environment of submarine subjected to underwater explosion impact loads[J].Journal of Harbin Engineering University,2006, 27(3):372-376.

[2]古滨，郎天齐，刘翠丹. 基于样本库方法的船舶冲击环境预报[J].舰船科学技术,2013, 35(8):12-17.

GU Bin, LANG Tian-qi, LIU Cui-dan. Research on shock environment of ship based on sample library method[J].Ship Science and Technology,2013, 35(8):12-17.

[3]Zhang A M, Zeng L Y, Cheng X D, et al.The evaluation method of total damage to ship in underwater explosion[J]. Applied Ocean Research. 2011, 33(2):240-251.

[4]冯麟涵，姚熊亮，汪玉. 基于本征函数的舰船冲击环境工程化预报方法[J].中国造船,2010,51(3):65-76.

FENG Lin-han, YAO Xiong-liang, WANG Yu. Engeering prediction method of ship impulsive environment based on empirical eigenfunction[J].Shipbuilding of China,2010,51(3):65-76.

[5]Keil A H.The response of ships to underwater explosions[J]. Annual Meeting of The SNAME, New York, 1961, 69:366-410.

[6]Geers T L. Excitation of an elastic cylindrical shell by a transient acousticWave[J]. Apply Mechs. 1969, 36: 459-469.

[7]Cole R H. Underwaterexplosion[M]. New Jersey: Princeton University Press, 1948.

[8]Geers T L, Hunter K S. An integrated wave-effects model for an underwater explosion bubble[J]. Journal of the Acoustical Society of America,2002, 111(4):1584-1601.

[9]Smith P D, Hetherington J G. Blast and ballistic loading of structures[M]. London:Butterworth-Heinemann Ltd., 1994.

[10]Geers T L. Doubly asymptotic approximations for transient motions of submerged structures [J]. The Journal of the Acoustical Society of America. 1987, 64:1500-1508.

[11]姚熊亮，徐小刚，张凤香. 流场网格划分对水下爆炸结构响应的影响[J]. 哈尔滨工程大学学报，2003,24(3):237-244.

YAO Xiong-liang, XU Xiao-gang, ZHANG Feng-xiang. Influence of fluid gridding on structural response of underwater explosion[J]. Journal of Harbin Engineering University, 2003, 24(3):237-244.

[12]Zhang A M, Zhou W X, Wang S P, et al. Dynamic response of the non-contact underwater explosion on naval equipment[J]. Marine Structures, 2011, 24:396-411.

[13]刘云龙,田昭丽,张阿漫.水下爆炸作用下单双层圆柱壳结构冲击损伤特性研究[J].振动与冲击,2014, 33(22):178-182.

LIU Yun-long, TIAN Zhao-li, ZHANG A-man. Damage of cylindrical shell structure subjected to underwater explosion loading[J].Journal of Vibration and Shock,2014, 33(22):178-182.

[14]章振华,谌勇,肖锋,等.敷设超弹性覆盖层舰船水下爆炸冲击实验与仿真分析[J].振动与冲击,2014,33(10):106-112.

ZHANG Zhen-hua, CHEN Yong, XIAO Feng, et al. Underwater explosion tests and simulation for ships with hyper-elastic coating[J].Journal of Vibration and Shock,2014, 33(10):106-112.

[15]Yao X L, Guo J, Feng L H,et al. Comparability research on impulsive response of double stiffened cylindrical shells subjected to underwater explosion[J]. International Journal of Impact Engineering, 2009, 36(5): 754-762.

[16]姚熊亮，郭君，曹宇，等.在水下爆炸冲击波作用下的新型冲击因子[J]. 中国造船，2008，49(2)：52-59.

YAO Xiong-liang, GUO Jun, CAO Yu, et al. New impulsive factor subjected to underwater explosive shock wave.[J]. Shipbuilding of China, 2008, 49(2):52-59.