P波段腔体滤波器的小型化设计∗

汤艳燕,卢晓鹏,2,张玉梅

(1.中国电子科技集团公司第三十八研究所,安徽合肥230088;2.孔径阵列与空间探测安徽省重点实验室,安徽合肥230088)

0 引言

众所周知,滤波器是雷达系统中不可缺少的选频器件之一。特别是在有源相控阵雷达系统中,DAM中每一个收发通道的后面都需要有一组接收预选[1]和发射滤波器。滤波器性能的好坏,直接影响雷达系统的抗干扰能力、对外杂散和谐波抑制能力。且一部雷达系统对滤波器的用量需求相当大,所以对于P波段雷达系统来说,研制出小体积、重量轻、驻波小、低损耗、高矩形系数和高次谐波抑制能力的滤波器尤为重要。

1 P波段滤波器的选择与设计原理

由于本滤波器的工作频率低、功率容量大且技术指标要求苛刻。一般的LC、介质、声表等滤波器可以实现低频段的小型化,但很难实现小损耗和大功率;微带或带状线滤波器可实现宽带和系统要求的大功率,但在P波段很难实现小型化,导致其高次谐波抑制能力差;螺旋腔体滤波器可以实现小型化和大功率,但很难实现宽带;只有同轴梳状腔体滤波器可以选择,但常规的同轴梳状滤波器也很难实现高次谐波的抑制。而本文中的接收滤波器要求二次谐波、三次谐波都在80 dB以上;发射滤波器考虑到有大功率要求,滤波器的阶数不宜过多,否则功率容量会受影响。

通常,同轴腔体带通滤波器中心导体长度选择约为λ0/2(λ0为通带中心频率对应的波长),特性阻抗Zc为75Ω[2]可实现小损耗,接入点位置离短路面高度为L1。将六腔分解为(1,2),(2,3),(3,4),(4,5),(5,6)五对耦合腔。用5对理想耦合线表示,其单线特性阻抗Z0为75Ω。考虑到实际腔体中存在损耗,耦合线对的奇偶模阻抗分别为(Ze12,Zo12),(Ze23,Zo23),(Ze34,Zo34),(Ze45,Zo45),(Ze56,Zo56),输入输出线阻抗为ZIO,构造结构模型如图1所示。一对互相耦合的同轴腔之间的耦合系数可以用其奇偶模特性阻抗表示为

因此,

奇偶模特性阻抗与特性阻抗Zc之间的关系为

再采用宽带滤波器设计方法和设计思路[2-3],利用Matlab编程可快速综合出各设计参数。将初始参数确定后,在高频设计软件中建立如图2所示的仿真模型,得到滤波器的最初设计曲线。再利用其优化功能进行图3中的各参数优化,优化后尺寸仅仅是常规腔体滤波器尺寸的1/3。七阶滤波器仿真结果如图4所示,七阶滤波器实测结果如图5所示。

七阶大功率滤波器大批量生产时指标实现情况:

● 通带频率:P波段26%带宽

● 通带内插损:≤0.5 dB

● 带外抑制:≥90 d B@48～223 MHz

≥80 dB@930 MHz～4f0

● 通带内驻波比:≤1.3

● 通带内相位一致性:优于±3.0°(大批量)

● 通带内幅度一致性:≤0.4 d B(大批量)

滤波器矩形系数好,二、三、四次谐波满足80 dB以上,无需太多调试,指标重复性好。

2 P波段大功率腔体滤波器的小型化实现

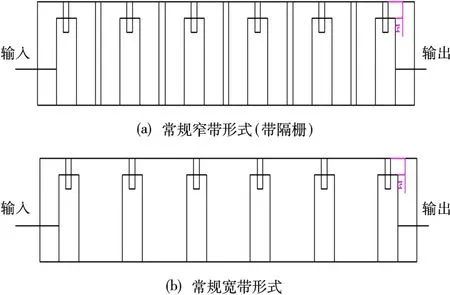
图1 常见的同轴滤波器示意图

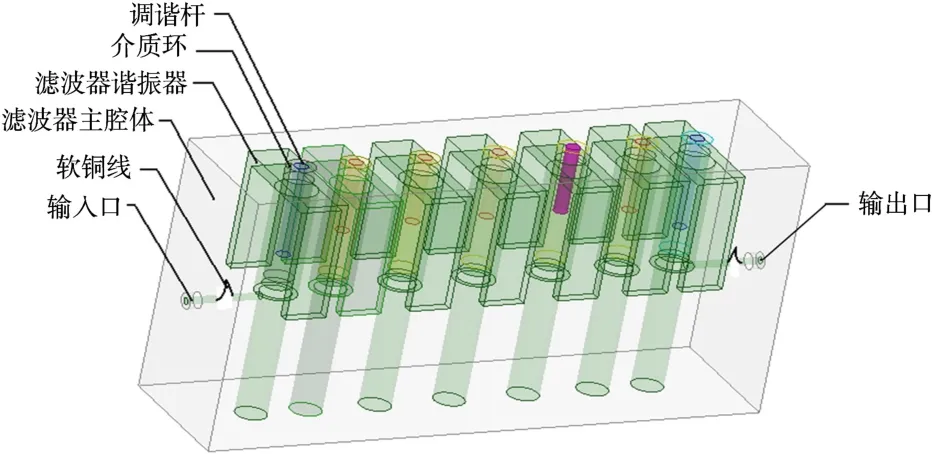
图2 小型化处理后的滤波器示意图

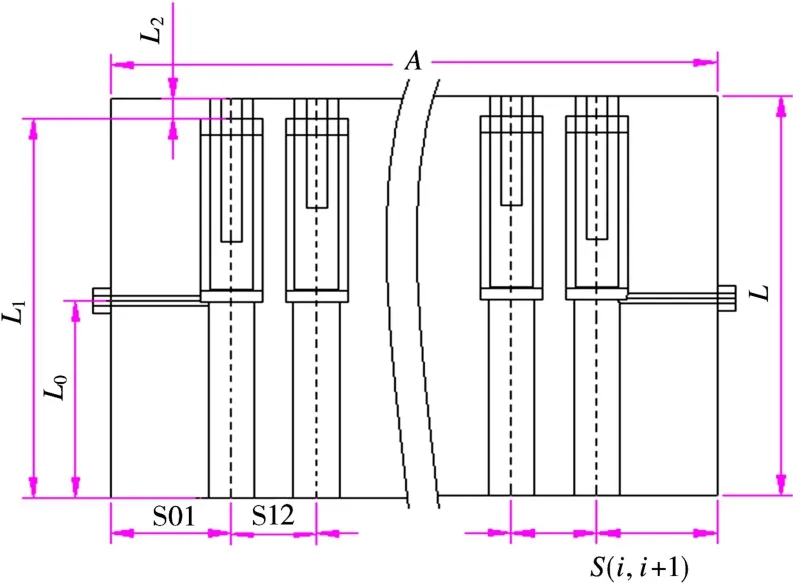
图3 滤波器腔体关键尺寸

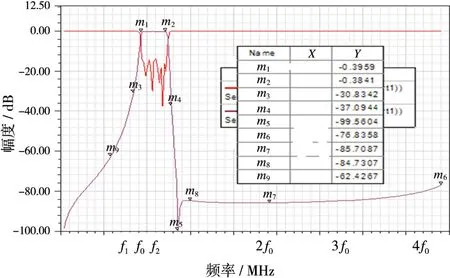
图4 滤波器仿真结果

图5 滤波器驻波和幅频特性实测曲线

滤波器的结构比一般无源器件复杂,且种类繁多,分析起来较困难。更重要的是,带通滤波器一般都是谐振结构,由于反复振荡,谐振器内的电磁场和电流比一般无源器件高许多,随之造成损耗功率也大得多。尤其在窄带滤波器的强谐振结构内部,场强往往可以达到端接传输线即馈线处的好几倍。于是,带通滤波器的功率容量问题和其他无源器件相比变得更为严峻和苛刻。带通滤波器内各谐振器排列顺序、摆放位置各不相同,它们所承受的场强和产生的损耗也不均匀,分析带通滤波器功率容量时必须找到对整体性能影响最大的谐振器,然后再作进一步分析。谐振器内部的电磁波无例外地处于驻波状态,即谐振器的场分布及热分布不像一般传输器件那样沿传播方向是均匀的。于是,不仅应当找到对滤波器性能起最关键作用的谐振器,而且应当找到该谐振器内部的场强最大点、最热点等关键位置。另一点值得特别注意的是,传输器件的功率容量一般仅随工作频率缓慢变化,而带通滤波器的功率容量随着自身频率响应发生快速变化,通带中心、边带、阻带内的功率承载能力相差悬殊。因此,在预测带通滤波器功率容量时,不但应当充分利用相应传输线结构功率容量评估理论的现有结果,而且应当从带通滤波器、谐振器本身的特性入手,更有效地抓住滤波器功率容量问题的实质。

本滤波器工作对功率容量要求高,主要考虑的工程因素有:海拔高度,驻波系数,工作环境的温度、湿度、物品污染。为确保可靠性,再留余量3 d B。发射支路上的滤波器,所需耐功率如下:峰功率2103 W,平均功率694.1 W。

从本滤波器的指标可以分析出,要实现滤波器二、三、四次高次谐波必须要进行谐振器的小型化设计。而P波段的频率低,谐振器的谐振频率决定其体积较大,且要满足2103 W峰功率、694.1 W平均功率要求,所以如何设计滤波器的谐振器成为本滤波器设计重点和难点。

根据系统分析出的功率要求,按式(4)初步设计出谐振器的腔体尺寸,再采用以下方法来减小谐振器的尺寸:

(1)滤波器开路端进行电容加载(功率容量小时谐振器的长度可与加载调谐杆尺寸相当)。

(2)谐振杆和调谐钉之间加耐功率的介质材料,增加滤波器Q值,减小滤波器体积;同时减小调谐钉的加载深度;另外谐振杆和调谐钉之间的距离较小,介质加载避免了外因造成的调谐钉和谐振杆短路。

(3)根据滤波器的带宽和阶数选择谐振器的形式,一般UIR形适合带宽宽、阶数少的情况,相同带宽在阶数较多的情况下可采用SIR形式[4-5],SIR形式可灵活控制高次谐波和缩减腔体尺寸。

(4)在方法(1)的基础上进行谐振器的变形,如图2所示的T形或U形端,T形端面和U形端面与腔体形成大电容,可进一步减小谐振器同轴电容加载深度[6],且本身的散热效果更好。

采用上述方法实现了P波段滤波器的小型化,从而实现了高次谐波的抑制,且功率容量满足雷达系统提出的苛刻指标要求。

有关文献给出了击穿场强的近似计算公式:

式中:

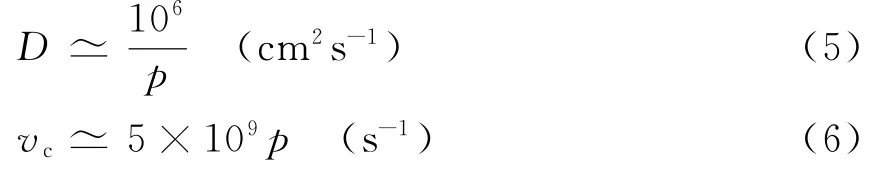
p为大气压强;τp为脉冲宽度;Leff为有效扩散路径(≈2倍间隙);击穿场强Ep=2.26×106V/m。

图6给出了输入端用2 800 W功率激励时的强分布结果。图7给出了P波段大功率滤波器的实物图。

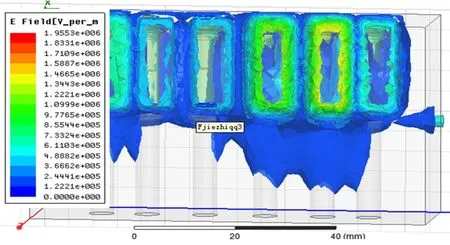
图6 2 800 W激励时滤波器场强分布仿真结果

图7 大功率滤波器实物图

3 结束语

本文设计了一种低频段的大功率腔体滤波器,经过仿真和实测结果对比表明,滤波器实现了结构紧凑、通带内的插入损耗小且带外抑制和高次谐波抑制能力强。在P波段实现了滤波器的小型化,高抑制、大功率,很好地满足了工程上的苛刻指标需求。经过大批量的流水线生产制造,按首件调试后的尺寸重复装配指标一致性好、调试量少、可靠性高,已经过某雷达系统的充分验证。

[1]伍小保,王冰,郑世连,等.米波雷达射频数字化接收机抗干扰设计[J].雷达科学与技术,2015,13(2):215-218.

WU Xiaobao,WANG Bing,ZHENG Shilian,et al.Anti-Jamming Design of RF Digitalized Receiver in VHF Radar[J].Radar Science and Technology,2015,13(2):215-218.(in Chinese)

[2]TEMES G C,MITRA S K.现代滤波器理论与设计[M].王志洁,译.北京:人民邮电出版社,1984.

[3]MAKIMOTO M,YAMASHITA S.无线通信中的微波谐振器与滤波器[M].赵宏锦,译.北京:国防工业出版社,2002:13-45.

[4]王云秀.无线通信系统中小型化微带滤波器的研究[D].成都:电子科技大学,2008:23-25.

[5]WANG Yunxiu,WANG Bingzhong,WANG Jianpeng.A Tri-Section Stepped Impedance Bandpass Filter with Harmonic Suppression[C]∥7th International Conference on ASIC,Guilin:IEEE,2007:592-595.

[6]WANG Y,YU M.True Inline Cross-Coupled Coaxial Cavity Filters[J].IEEE Trans on Microwave Theory and Techniques,2009,57(12):2958-2965.