基于空间时频分布的高频雷达接收阵校正∗
(哈尔滨工业大学(威海)信息与电气工程学院,山东威海264209)
0 引言
高频地波雷达利用超分辨的信号处理算法实现信号的到达角(Direction of Arrival,DOA)估计[1-2],而这类算法的性能极大地受制于阵列误差,当误差严重时甚至导致该类算法失效[3]。阵列校正可以分为有源校正和无源校正两类。有源校正需要在天线阵远场放置一个以上的已知方向信源,而对于高频地波雷达而言,远场位置在海面上,信源架设困难[4],而且天线阵误差随着外界散射场的变化而变化[5],因此有源校正不太适合高频地波雷达;无源校正是利用正常目标的回波信号,通过阵列信号处理的方式,对目标的方位与阵列的误差进行联合估计,从而达到实时校正的目的。目前高频地波雷达多采用无源校正方式进行接收阵校正[6]。
无源校正的研究开始于20世纪80年代,主要的校正算法分为两大类。第一类以1985年Paulraj与Kallath提出的利用无误差情况下空间相关矩阵的Toeplitz结构的方法[7]为代表,该类方法主要利用空间相关矩阵规律性的结构;第二类以1989年Weiss与Friedlander提出的通过构造代价函数的方法[8-9]为代表,该类方法将误差校正转变为参数优化问题。第一类算法要求较为准确地估计出校正目标的空间相关矩阵。时域信号由于未经过多普勒分离,信号中包含整个频段的信息,因此信噪比较低,很难满足校正要求,而且实际应用中也很难找到包含单个目标的距离门。同时,高频地波雷达需要较长的相干积累周期以获得较高的信噪比,通常一个积累周期需要2~3 min,这会导致同一目标可用的频域快拍数很少[10]。文献[11]证明了空间时频分布(Spatial Time-Frequency Distribution,STFD)矩阵与空间相关矩阵具有相似的结构,并可以利用其进行目标的DOA估计。
本文针对上述阵列校正中空间相关矩阵估计困难的问题,首次利用目标的空间时频分布矩阵代替空间相关矩阵进行阵列校正,并使用蒙特卡洛法仿真分析了不同信噪比下两种方法的校正结果,最后使用该方法对实际数据进行处理,验证了该方法在实际应用中的效果。
1 理论部分
1.1 阵列的幅相误差模型
假设天线阵为图1所示的M元均匀线阵,目标信号源来自方位角θ,则第m(m=1,2,…,M)个阵元接收到的信号为
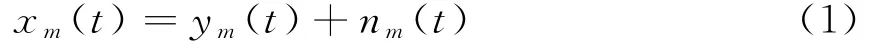
式中:xm(t)表示目标信号;nm(t)表示加性噪声;ym(t)=ejτms(t),τm为信号到第m个阵元的入射时延。以第一个阵元为参考阵元,τm可写成:
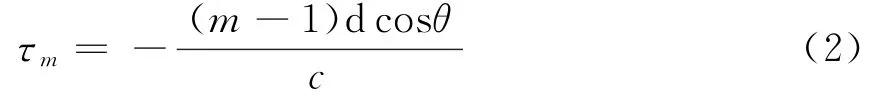
均匀线阵无法测目标的俯仰角,因此此处不再考虑俯仰角;c表示电磁波的传播速度。
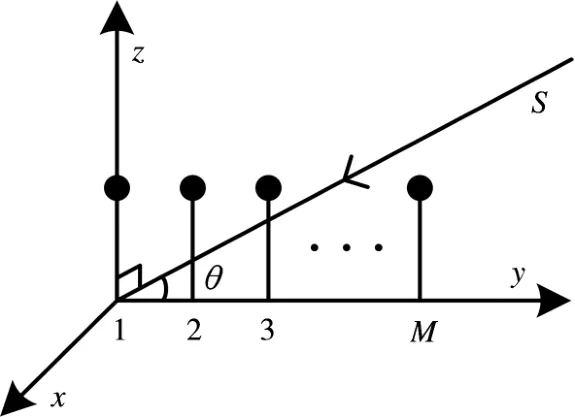
图1 均匀线阵
将阵列的幅相误差考虑在内,阵元的接收信号可改写成:
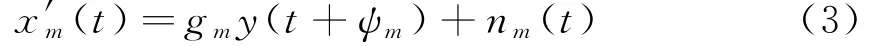
式中:gm表示第m个阵元的幅度误差;ψm表示阵元m上的等效信号时延误差。写成矩阵形式为

式中:Γ=diag{g1ejφ1,g2ejφ2,…,gMejφM},g与φ分别表示各阵元的幅度与相位误差;X(t)=[x1(t),x2(t),…,xM(t)]T,X′(t)=[x′1(t),x′2(t),…,x′M(t)]T,T表示转置。
1.2 空间时频分布矩阵
空间时频分布(STFD)的定义式为
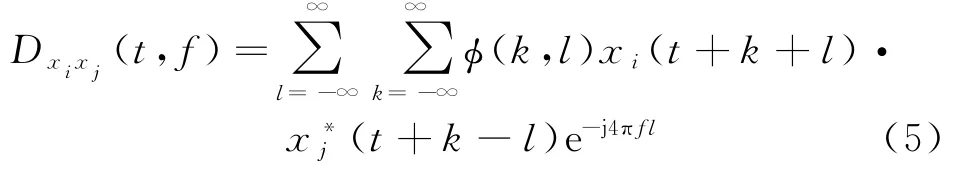
式中:ϕ(k,l)表示时频核,k与f分别表示时间参量与频率参量;i与j表示矩阵的行和列,且i,j=1,2,…,M;xi与xj表示不同阵元接收到同一信源的数据;符号∗代表共轭运算。将STFD写成矩阵形式为
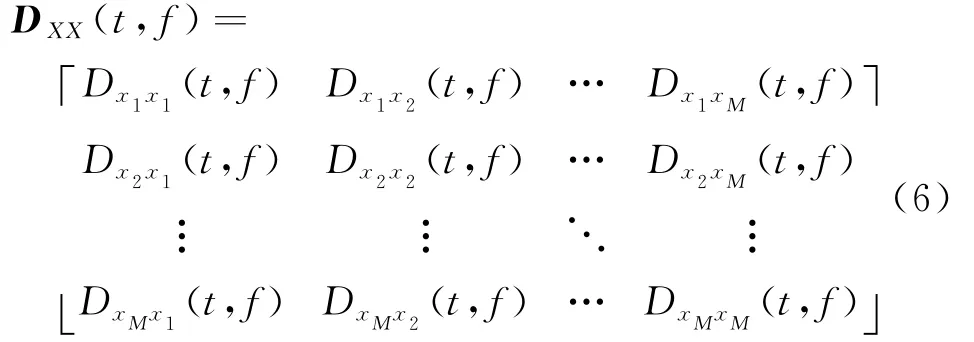
将式(1)代入式(5),DXX展开为如下形式:
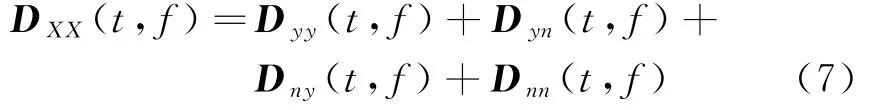
由假设条件,噪声与信源独立可知
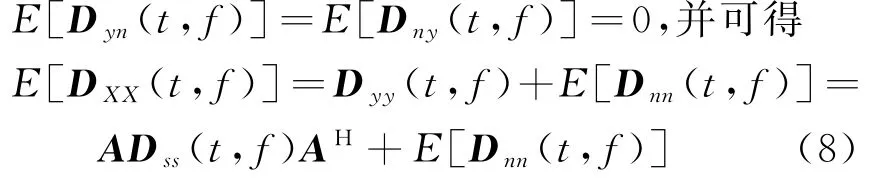
式中:A表示信源X在θ方向的导向矢量;E[·]表示期望运算。将式(4)代入式(8)可得
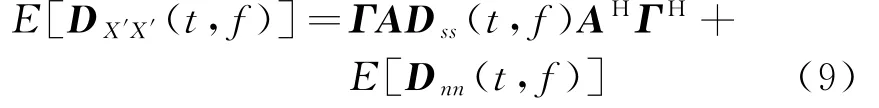
在实际数据处理中,可取多个时频点,通过下式估计出目标信号的STFD矩阵:
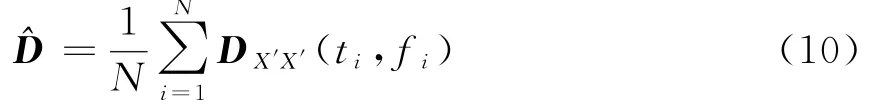
式中,N为时频点个数。
1.3 STFD信噪比提升分析
设时频窗宽度为L,xi(t)=Wiejwi(t),则时频矩阵的对角线第i个元素如下式所示:
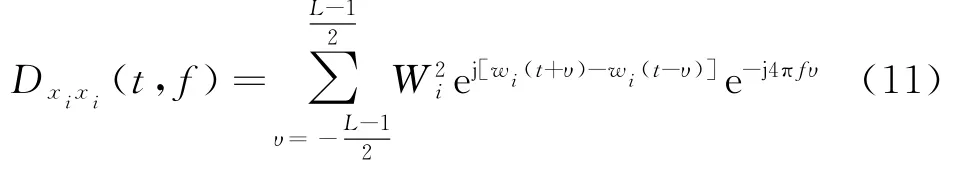
式中,Wi表示第i个信号的幅度,wi(t)表示其相位。则沿着时频点的第i个信号的瞬时频率为

并且wi(t+υ)-wi(t-υ)-4πfi(t)υ≈0,有下式成立:
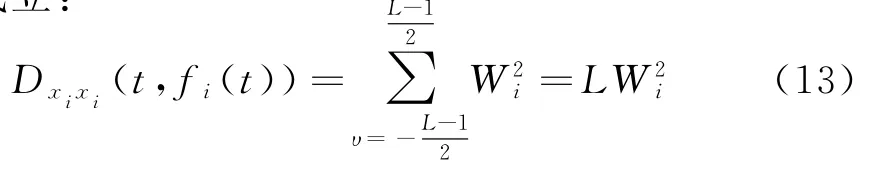
类似地,噪声的空时分布为
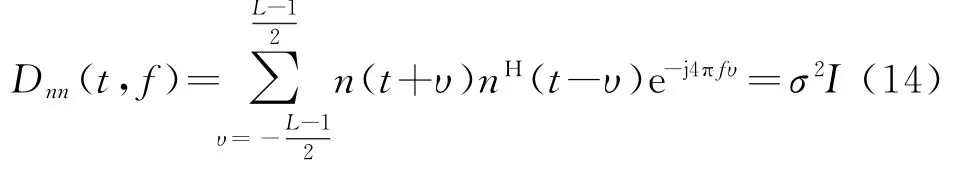
式中,σ2表示白噪声功率,I表示单位对角阵。由此可以看出,沿信号瞬时频率选择时频点,可以有效地将信噪比增强L倍。
1.4 阵列的幅相误差校正方法
文献[12-13]中提出了一种阵列校正的新方法,主要利用空间相关矩阵中元素相位线性变化的规律,运用曲线拟合等方法估计出阵列的相位误差。本文拟使用空间时频矩阵代替空间相关矩阵对相位和幅度误差进行估计。相位误差估计公式如下:式中:ϕm,1为^D的相位矩阵Φ的第m行、第1列的元素;^α为估计出的^D的相位变化斜率。
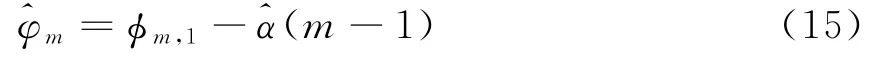
阵列的幅度误差可由STFD矩阵的主对角元素进行估计。由式(9)易知:

当信噪比较高时,Dxmxm(t,f)=Dx1x1(t,f)。以第一阵元为参考阵元,可估计出各阵元的相对幅度误差^gm为
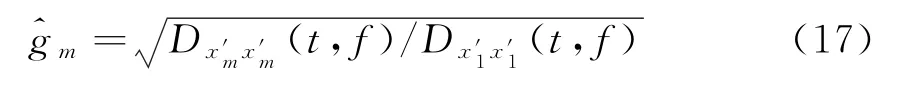
2 仿真分析
使用蒙特卡洛法,在不同信噪比下,仿真对比空间时频分布矩阵STFD与空间相关矩阵SCM的阵列校正效果。
仿真实验中,设定阵元数目为16,目标信号的来波方向为20°,蒙特卡洛循环次数为100,每次实验的幅相误差由式(18)、(19)随机产生:
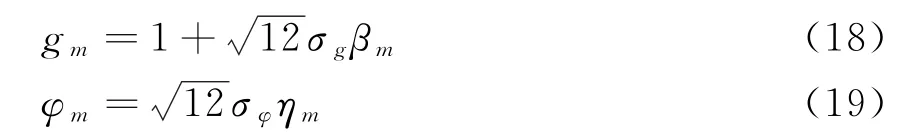
式中:βm和ηm为[-0.5,0.5]上的均匀分布;σg为幅度误差方差,σφ为相位误差方差。每个阵元的平均求解误差由下式得到:
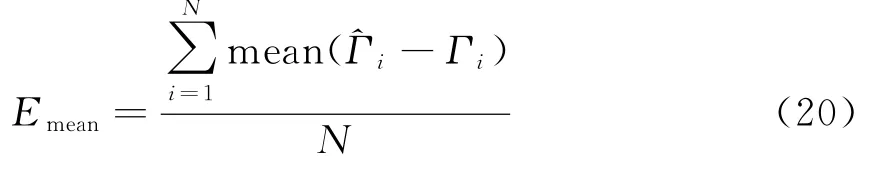
式中:Γi表示每次蒙特卡洛实验随机产生的幅相误差矩阵;^Γi表示校准算法估计出的误差矩阵;N表示蒙特卡洛实验次数;mean(·)表示对矩阵(·)求平均。
图2是在σg=0.5,σφ=15的情况下,不同信噪比时每个阵元的平均误差。可以看出,基于STFD矩阵求解阵列幅相误差比传统利用空间相关矩阵对信噪比的要求降低了5 d B左右。这主要是因为通过时频点的选取滤除了大部分噪声,降低了噪声功率,从而提高了信噪比。另外,当信噪比高于15 dB之后,两种校正效果大致相同。图3为在SNR=0,σg=0.5的情况下,通过改变σφ获得的实验结果。同样可以看出,在误差容忍度不变的情况下,基于STFD矩阵阵列校正能力提高了10°左右的校正能力。
文献[14-15]中已经给出了幅相误差对雷达性能的影响。其中最主要的影响在于接收阵旁瓣水平的提高,因此本文将通过对比校正前后的旁瓣水平来估计校正效果。获得最小平均旁瓣所需的权值为
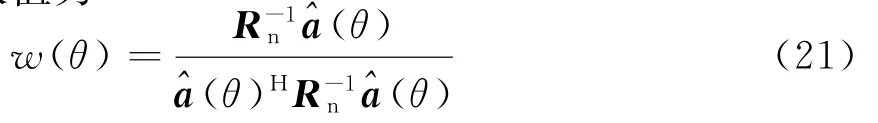
式中,^a(θ)为校正后的阵列导向矢量,Rn为噪声的相关矩阵。对于方向θ的波束形成为
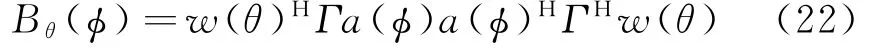
式中,θ为波束方向,ϕ为目标方向。使用式(22)即可计算出旁瓣水平。图4展示的是在信噪比为10 d B时通过蒙特卡洛实验获得的阵列旁瓣峰值水平。从图中可以看出,校正后旁瓣普遍降低了5 dB以上,而且使用STFD矩阵相较于传统SCM方法,旁瓣再次降低3 dB左右,而且更加趋近于无幅相误差时的旁瓣水平。
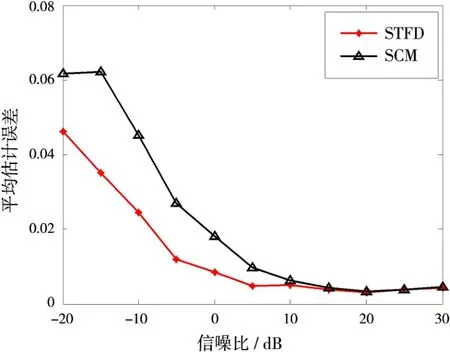
图2 不同信噪比下的对比
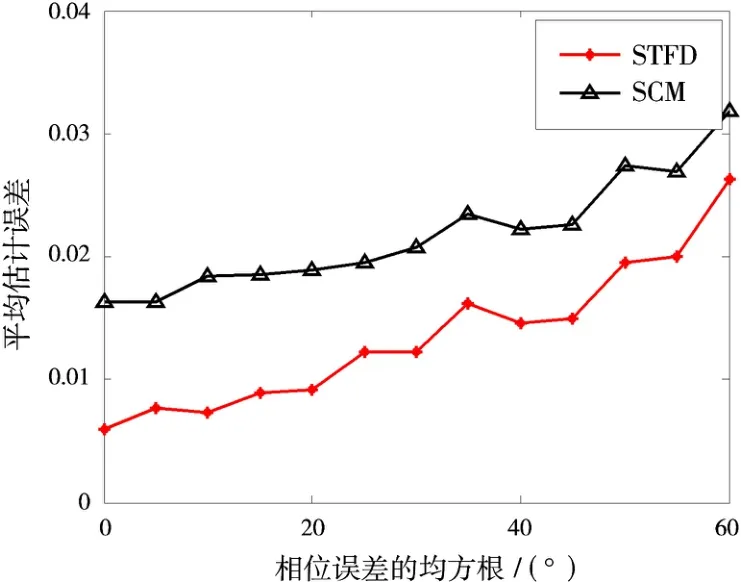
图3 不同相位误差情况下的对比

图4 旁瓣峰值水平
3 实测数据处理
本文采用的雷达数据来自于哈工大(威海)高频地波雷达站,接收阵为8元均匀线阵,相干积累周期150 s,距离分辨单元1.5 km,有效距离门个数194。由于高频地波雷达常以积累周期作为数据处理的基本时间单位,因此本文也以此为单位进行阵列校正。取第一个阵元一个积累周期的数据,作距离多普勒变换,得到图5所示的R-D谱。
图6为第80个距离门的剖面图,可以看到在120 km处有一个速度为-6 m/s的目标。图7为使用W-V分布做出的时频分布图,可以看到在Doppler对应位置有图6所示目标,并显示出该目标的即时速度。
对图7中[300~600,-6.5~-7.5]之间的300个谱进行谱峰搜索可得到300个时频点。对这些时频点利用式(9)可得300个STFD矩阵,最后利用式(10)即可得到STFD矩阵的估计值^D。将^D运用到上文中的校正算法中,便可获得该积累周期的幅相误差,结果如图8所示。图9为使用该结果校正前后目标常规波束形成的空间谱对比,可以看到校正前后旁瓣水平下降,并且由STFD进行阵列校正的效果优于传统SCM方法。
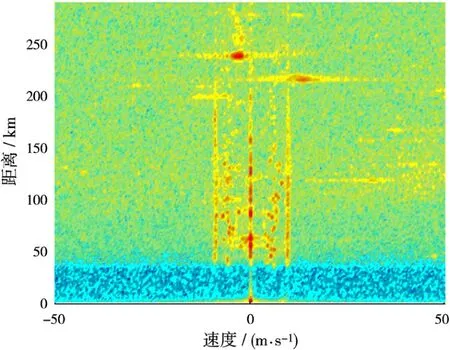
图5 第一阵元的R-D谱
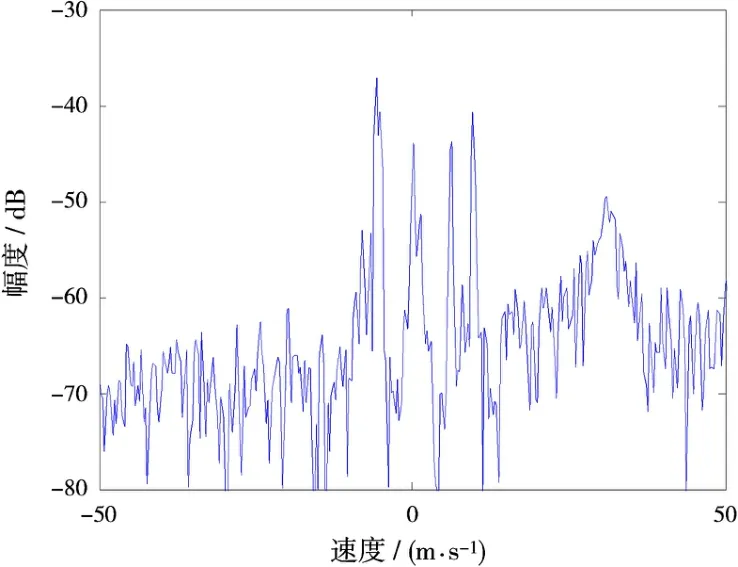
图6 第80距离门的剖面图
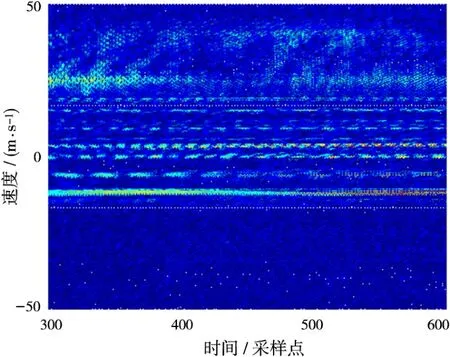
图7 103距离门一个积累周期的时频分布图
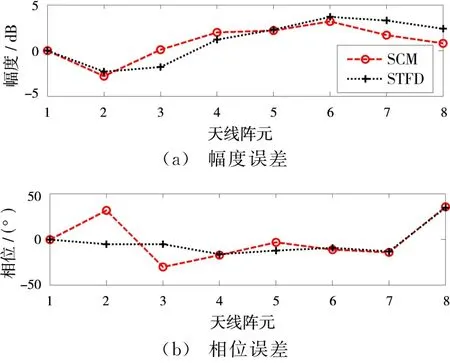
图8 阵列幅相误差值
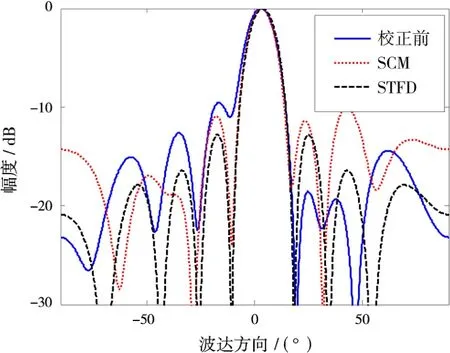
图9 目标常规波束形成空间谱
4 结束语
本文提出了一种使用空间时频分布矩阵代替传统的空间相关矩阵,对高频地波雷达接收阵列的幅相误差进行校正的新方法。相比传统基于SCM的阵列校正方法,本文提出的新方法对信噪比低于15 dB情况下校正效果改善尤为明显,大大提高了接收阵列校正的适应范围,具有一定的实际应用价值。通过计算机仿真和实际数据检验,验证了该方法的有效性。但是,使用STFD进行阵列校正时,时频点的选取较为困难,而且由于所需STFD矩阵数量较多,其计算量也比传统方法要大。因此,如何快捷、准确地选取合适的时频点,以及如何降低STFD算法的计算量,将是后续研究的重点。
[1]李晓东,于长军,陈磊,等.一种用于高频雷达探测性能评估的方法[J].雷达科学与技术,2015,13(6):587-591.
LI Xiaodong,YU Changjun,CHEN Lei,et al.A Method for Detection Performance Evaluation of High Frequency Surface Wave Radar[J].Radar Science and Technology,2015,13(6):587-591.(in Chinese)
[2]BRUNO L,BRACA P,HORSTMANN J,et al.Experimental Evaluation of the Range-Doppler Coupling on HF Surface Wave Radars[J].IEEE Geoscience and Remote Sensing Letters,2013,10(4):850-854.
[3]SCHMID C M,SCHUSTER S,FEGER R,et al.On the Effects of Calibration Errors and Mutual Coupling on the Beam Pattern of an Antenna Array[J].IEEE Trans on Antennas and Propagation,2013,61(8):4063-4072.
[4]CAI W,XIE J,SUN M.Space-Time Distribution of the First-Order Sea Clutter in High Frequency Surface Wave Radar on a Moving Shipborne Platform[C]∥Fifth International Conference on Instrumentation and Measurement,Computer,Communication and Control,Qinhuangdao:IEEE,2015:1408-1412.
[5]WEISS C,ZOUBIR A M.Robust High-Resolution DOA Estimation with Array Pre-Calibration[C]∥22nd European Signal Processing Conference,Lisbon:IEEE,2014:1049-1052.
[6]龙超.高频地波雷达阵列优化与校正算法研究[D].武汉:武汉大学,2012:83-90.
[7]PAULRAJ A,KAILATH T.Direction of Arrival Estimation by Eigenstructure Methods with Unknown Sensor Gain and Phase[C]∥IEEE International Conference on Acoustics,Speech and Signal Processing,Tampa,FL:IEEE,1985:640-643.
[8]WEISS A J,FRIEDLANDER B.Array Shape Calibration Using Sources in Unknown Locations:A Maximum Likelihood Approach[C]∥International Conference on Acoustics,Speech and Signal Processing,New York:IEEE,1988:2670-2673.
[9]FRIEDLANDER B,WEISS A J.Eigenstructure Methods for Direction Finding with Sensor Gain and Phase Uncertainties[C]∥International Conference on Acoustics,Speech and Signal Processing,New York:IEEE,1988:2681-2684.
[10]于文启,陈建文,杨春山.一种天波超视距雷达电离层相位污染的校正算法[J].雷达科学与技术,2015,13(6):660-666.
YU Wenqi,CHEN Jianwen,YANG Chunshan.A Correction Algorithm for Ionopheric Phase Contamination in Sky-Wave Over-the-Horizon Radar[J].Radar Science and Technology,2015,13(6):660-666.(in Chinese)
[11]AMIN M G,ZHANG Y.Direction Finding Based on Spatial Time-Frequency Distribution Matrices[J].Digital Signal Processing,2000,10(4):325-339.
[12]SONG Xiaoguo,WEI Yinsheng,CUI Yan,et al.A Novel Array Calibration Method Based on Spatial Correlation Matrix for HFSWR[C]∥10th International Conference on Signal Processing,Beijing:IEEE,2010:344-347.
[13]WEI Yinsheng,SONG Xiaoguo,TAN Jiubin.An Array Calibration Method Using Spatial Correlation Properties for HFSWR[C]∥CIE International Conference on Radar,Chengdu:IEEE,2011:364-367.
[14]SOLOMONI S D,ABRAMOVICH Y I,GRAY D A.OTH Radar Antenna Array Calibration Analysis[C]∥4th International Symposium on Signal Processing and Its Applications,Gold Coast:IEEE,1996:471-474.
[15]SOLOMON I S D,GRAY D A,ABRAMOVICH Y I,et al.Receiver Array Calibration Using Disparate Sources[J].IEEE Trans on Antennas and Propagation,1999,47(3):496-505.

