基于压缩感知的多径LFM信号参数估计∗
(空军预警学院,湖北武汉430019)
0 引言
线性调频信号由于具有大的时宽、带宽积,被脉冲压缩体制雷达广泛采用,有效解决了雷达系统作用距离和距离分辨率之间的矛盾。因而,对线性调频信号的检测和估计一直是雷达对抗信息处理领域的热点研究问题。在实际情况中,由于地面反射作用造成的多径效应使雷达对抗侦察设备接收到的雷达回波信号通常是直接路径与反射路径两种信号的叠加,造成信号在幅度和相位的变化[1-3]。多径分量包含有目标的重要信息,但却经常影响雷达对抗侦收设备的检测与跟踪性能,对目标检测和参数估计带来较大影响[4]。因此,对线性调频信号的多径分量参数估计是当前亟需研究的热点问题。
很多专家和学者采用不同方法在此方面进行尝试,并取得一些研究成果,比如盲信号分离技术、循环相关变换法等均可对多径分量进行参数估计。其中,盲信号分离技术即是运用矩阵论思想,通过求解特征向量进行源信号估计,抑制多径效应和噪声,提取雷达发射的直接波信号[5]。然而该方法依赖高信噪比,在低信噪比条件下,源信号估计效果降低,难以提取准确的时延(即相位)信息。若弥补低信噪比将大大增加算法复杂度,且信号衰减(或幅度)信息在处理中被丢失。循环相关变换法是利用部分雷达信号(如LFM信号、BPSK信号等)的循环平稳特性,结合循环频率域的信号分离技术估计多径分量的特征参数[6-7]。该方法能用来估计未知多径个数情况下的信号参数,且适用于较低信噪比情况的参数估计。然而,当多径分量各时延间隔很小以及背景噪声很大时,直接利用循环互相关谱进行时延参数估计较困难,即对时延信息的分辨率不够高。
近年来,压缩感知作为一种新型信号处理理论,掀起了国内外专家学者的应用与研究热潮。压缩感知又称压缩采样,是一种与数据采集的传统Nyquist方法不同的新采样技术[8]。该理论认为,只要信号在某种变换域下具有稀疏性,就可在远小于Nyquist采样率的条件下,用随机采样获取信号的离散样本,然后通过非线性重建算法恢复信号[9]。随着压缩感知理论的完善,已在遥测遥感[10]、医学图像处理[11]、电力系统[12]等信号分析处理领域应用。本文提出将压缩感知理论应用于线性调频信号多径分量的参数估计,通过对雷达回波进行简化建模,分析了此方法用于多径分量参数估计的可行性,并进行信号重构。实验结果证明,较其他诸如循环相关变换法、盲信号分离法等,新方法具有高时延分辨率、数据资源利用率以及估计精度等优势。
1 问题描述
1.1 LFM信号雷达回波简化模型
根据散射点模型,建立侦收端LFM信号的雷达回波简化模型,s(t)表示单路径LFM信号,y(t)表示多径信号,v(t)为测量噪声,得到简化的雷达回波即观测信号r(t):

即

式中:f0为载频;T为观测时长;k为调频率;K为接收LFM信号个数(即在时延基字典下为LFM信号的稀疏度);Ai和τi分别为i路径下对应衰减及时延,为待测量。
将式(2)表示为数字形式,即
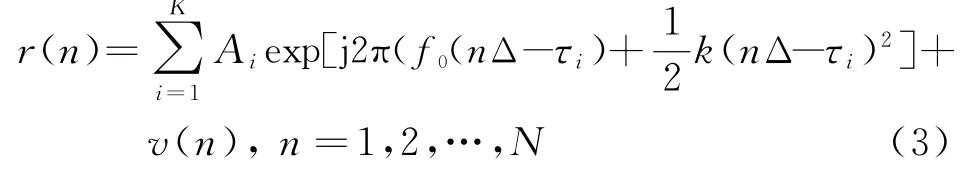
式中,nΔ为t的数字化表示,N为T的数字化表示。
1.2 LFM信号多径分量参数估计问题描述
多径分量参数估计问题是对接收到的一组类似回波的LFM直达及延迟信号的混叠和信号的N个数据,解算其包含的多径分量衰减及时延值,并观察其对应分量的衰减。利用多个时刻的回波信号将考虑的时延范围划分为{τ1,τ2,…,τi,…,τL},i∈[1,L],其中τ1=0为直达信号,τi=(i-1)Ts,Ts为设定的时延搜索间隔,τL=τmax为最大时延拓展。由于多径分量多成簇分布,使得各多径分量之间的时延间隔远大于时延搜索间隔Ts,从而使得{τ1,τ2,…,τi,…,τL},i∈ [1,L]中的非零个数K很少,即K≪L,满足信号稀疏性特性,由此可作为利用压缩感知法进行多径分量参数估计的理论基础。用表示实际存在的多径分量,表示实际不存在的多径分量,有如图1所示信号多径分量稀疏化的图形表示。

图1 多径分量稀疏化图形表示
由于回波信号的多径分量作为待估参数,是连续且随机分布的,因而并不能保证每个分量均在设定的离散网格上,即多径分量的时延参数不一定全部精确落在{τ1,τ2,…,τi,…,τL}这一网格上,此问题超出本文讨论范围,可通过一般模型误差的压缩感知理论加以解决。为分析方便,不妨假设时延搜索间隔Ts足够精细,则各多径分量均可定位于搜索网格上。
2 基于压缩感知的多径LFM信号参数估计
压缩感知理论表明,当信号可压缩[13]或可通过稀疏信号近似表达时,通过采集少量线性、非自适应的测量值,就可实现信号的准确或近似重构。根据接收到的一组LFM雷达回波信号,建立压缩感知单量测向量(SVM)模型[14]。
假设长度为K的待测复信号x=[x1,x2,…,xK]T可以用某稀疏基矩阵ψ=[ψ1,ψ2,…,ψL]的线性组合来表示,即

式中,z为一个L×1维的具有K(K<L)稀疏的向量。那么存在一个与ψ不相关的,即满足RIP条件[8]的N×K维测量矩阵Φ,使
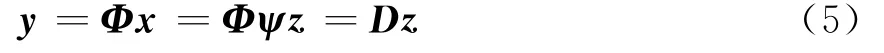
式中D为N×L维矩阵,称为传感矩阵,亦可看成是z关于y的推广的测量矩阵。
由压缩感知理论可知,如果矩阵D满足约束等距性(Restricted Isometry Property,RIP)等稀疏重构条件[15],则可以通过利用以下L0范数意义的优化问题以高概率精确重构稀疏信号x。

综上所述,利用压缩感知理论实现LFM信号多径分量参数估计,需要重点研究三方面内容,即信号的稀疏表示、测量矩阵的设计以及信号的重构算法。
2.1 信号的稀疏表示
根据上节所述雷达回波模型及稀疏性分析,建立LFM信号多径分量估计模型:

式中:r=[r1,r2,…,rN]T即接收到的N个回波信号;A为K稀疏的L×1维向量,代表L个可能的多径分量对应的衰减值;S=[S1,S2,…,Si,…,SL]为可能的多径分量构成的矩阵,Si=s(n-τi)=ex p[j2π(f0(nΔ-τi)+k(nΔ-τi)2],v=[v1,v2,…,vN]T,v是服从均值为0、方差为δ2的高斯分布的加性白噪声。
故可将式(7)进一步表示为

显然,S即代表式(4)中稀疏基矩阵ψ。传统的压缩感知理论选择正交基作为ψ,但由于正交基存在很大的局限性,稀疏分解的思想就是利用冗余原子库取代正交基函数,即将基用字典表示。原子库中包含的元素称为原子,可尽可能逼近信号结构,这样,可从字典中选择少数原子去最佳逼近信号[16]。
2.2 测量矩阵的设计
测量矩阵用于对原待测信号进行压缩观测,常用的测量矩阵有随机高斯矩阵、托普利兹矩阵、贝努利矩阵、局部哈达玛矩阵和傅里叶随机矩阵。
对于一个N×L维高斯随机矩阵Φ,当N=o(K ln(L))时,传感矩阵D在很大概率下具有RIP性质。而高斯随机矩阵与大多数固定正交基构成的矩阵不相关,即选其作测量矩阵Φ时,与稀疏变换基ψ不相关,使D满足RIP等稀疏重构性质。因此,选用多个服从N(0,1)独立正态分布的高斯随机变量作为测量矩阵Φ的元素,满足压缩感知理论对测量矩阵的设计要求。
2.3 信号的重构
信号的重构就是指从长度为N的测量向量y重构出原始信号x的过程,即对式(6)进行优化求解。
目前信号重构算法主要分三类,第一类是凸优化算法,包括最小全变差法(TV)、梯度投影算法(SPG)等;第二类是贪婪追踪算法,包括匹配追踪算法(MP)、正交匹配追踪算法(OMP)、稀疏自适应匹配追踪算法(SAMP)等;第三类是组合算法,包括随机傅里叶采样法、稀疏序列匹配追踪法等。重构信号时,凸优化算法虽计算过程较为复杂,但所需观测次数最少,采样效率最高,本文选择梯度投影算法进行信号重构。
凸优化算法利用了基追踪/基追踪去噪算法(Basis Pursuit/Basis Pursuit Denoise,BP/BPDN)模型,其思想是,当D满足RIP条件,且N≥c K·log2()时,可通过求解最小化L1范数[17]优化方程得到信号重构解,即式(6)可转换为
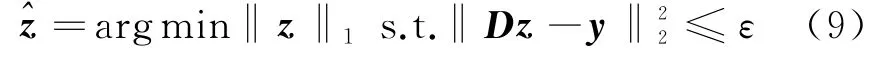
梯度投影算法(SPG)是一种用于解决BP/BPDN问题的凸优化方法,采用非单调线搜索策略,将谱投影梯度g和谱步长α分别作为搜索方向和步长,更新方向的选择取决于当前及前几次迭代点方向,利用式(10)投影算子产生每次迭代搜索的投影梯度路径。梯度投影算法(SPG)具有低复杂度、高重构精度和良好的全局收敛性的优点,且计算效率较高,适合求解大规模优化问题,适用于本文的稀疏随机测量重构。不受有界条件约束的SPG算法同样具有收敛性和有限步终止性[18]。

具体流程如下:
步骤1 初始化:稀疏估计值^z0=0;残差b0=y;初始梯度g0=-DTb0;初始步长α0∈[αmin,αmax];迭代次数t=1。
步骤2 迭代:重复步骤2直至满足迭代停止条件。
步骤2.1 线性迭代搜索策略更新本次迭代估计值:
步骤2.1.1 更新稀疏估计值和残差

步骤2.3 若‖bt‖2-(yTbt-τ‖gt‖∞)/‖bt‖2>δ,t=t+1,重复步骤2.2;否则,结束循环。
步骤3 输出稀疏估计值^z=^zt。(^zt-^zt-1)Tgt-1,进行步骤2.1.3;否则,αt-1=αt-1/2,重复步骤2.1.1。
步骤2.1.3 更新梯度gt=-DTbt。
步骤2.2 更新下次迭代谱步长:
步骤2.2.1 Δz=^zt-^zt-1;Δg=^gt-^gt-1。
3 仿真实验与分析
为了检验基于压缩感知法对LFM信号多径分量参数估计的性能,本文选择循环相关变换法作对比,根据不同情况下两种算法的解算结果进行性能分析及比较。实验中,设置LFM信号中心频率f0=1 M Hz,采样频率fs=2f0=2 M Hz,采样间隔Ts=1/fs,带宽B=0.5f0=0.5 M Hz,脉宽τp=200μs。
实验1 多径时延分辨率性能比较
实验中,多径分量数设M=3,多径衰减为{A1,A2,A3}={1,0.5,0.8},对应时延为{τ1,τ2,τ3}={0,100Ts,110Ts},信噪比SNR=10 dB,实验数据点取N=1 000。实验结果如图2和图3所示。

图2 实验1中压缩感知法解算结果1

图3 实验1中循环相关变换法解算结果1
由图2和图3可以看出,压缩感知法可清晰地看到3个峰值并对应了正确的时延值,衰减值也得到了较好估计,而循环相关变换法解算结果仅出现2个峰值,在100Ts附近波瓣展宽,解算失败。将时延值设为{τ1,τ2,τ3}={0,100Ts,150Ts},其余参数设置不变,可从图4和图5所示实验结果看到此时循环相关变换法已经可以解算出3个峰值,时延估计相对准确,但衰减值没有完全准确估计,然而压缩感知法可以准确估计时延及衰减,2种算法参数估计效果对比依然明显。从实验1可以看出,对LFM信号进行多径分量参数估计,压缩感知法较循环相关变换法具有更高的时延分辨率,对应的衰减也能得到较好估计。
实验2 数据资源利用率性能比较
实验中,多径分量数设M=3,多径衰减为{A1,A2,A3}={1,1,1},对应时延为{τ1,τ2,τ3}={0,100Ts,150Ts},信噪比SNR=10 dB,数据点分别取N=1 000和N=100进行采样。实验结果如图6、图7、图8和图9所示。

图4 实验1中压缩感知法解算结果2

图5 实验1中循环相关变换法解算结果2
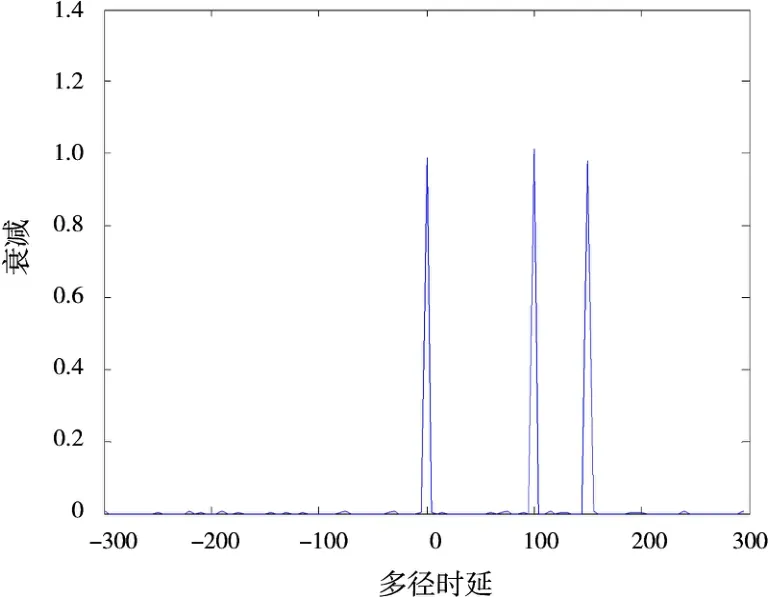
图6 实验2中压缩感知法N=1 000
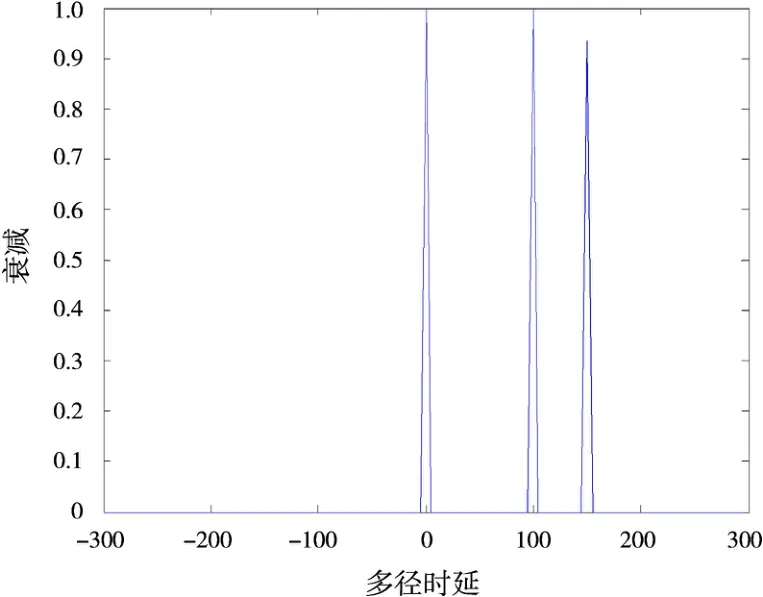
图7 实验2中压缩感知法N=100

图8 实验2中循环相关变换法N=1 000
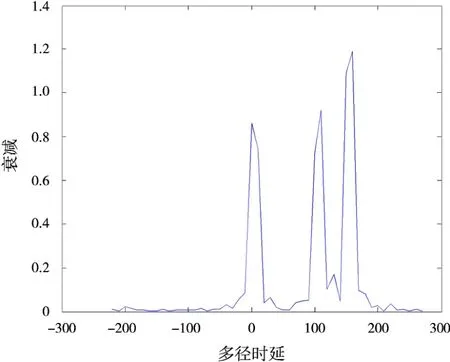
图9 实验2中循环相关变换法N=100
从解算结果看出,对压缩感知法,当数据点减少10倍时,依然可以很好地进行多径分量时延估计,效果并未发生显著变化,然而循环相关变化法在当数据率减少同样的倍数时,参数估计效果明显恶化。这是由于循环相关变换法是基于传统Nyquist采样定理的算法,当所选用数据点数确定时,参数估计精度即被确定,因而循环相关变化法的参数估计精度与数据点数密切相关,数据点数越多,估计越精确。然而现实情况中,数据丢失的情况并不少见,很可能只得到少量的原始数据,使得参数估计的精准度大大下降,难以较好地完成复杂电磁环境下的参数估计任务。压缩感知理论的参数估计精度由所建字典的精细度决定,当字典足够精细,包含的原子库足够充足,即可实现信号的精确重构。因而用此方法进行多径分量参数估计时具有高数据资源利用率,这也体现了用压缩感知进行多径分量参数估计的先进性。
为进一步证明压缩感知法用于多径分量参数估计的先进性,分析了在数据点N=100时,参数估计均方误差随SNR变化,取信噪比变化范围SNR=0~30 dB,步进为1 dB,做1 000次Monte-Carlo试验。从图10可以看出,压缩感知法随SNR增加估计精度逐步增大,且当SNR=0时均方误差EMS<0.16,在误差范围之内,仍然保持了良好的估计精度。可见,压缩感知法在低数据情况时依然具有较高的估计精度,再次体现了将此方法用于LFM信号多径分量参数估计的优越性。

图10 压缩感知法参数估计精度随SNR变化
4 结束语
本文研究了基于压缩感知的LFM信号多径分量参数估计,相对于传统方法,压缩感知法突破了Nyquist采样定律,可利用较少数据进行信号重构,具有更高的时延分辨率、数据资源利用率,并且在较少原始数据情况下仍可实现较高的估计精度,对于复杂电磁环境下的参数估计具有较高的实用价值。
[1]周志增,刘朋,顾荣军.多径对雷达探测性能的影响分析[J].太赫兹科学与电子信息学报,2013,11(5):736-740.
[2]莫约利,门加利.视距微波传播[M].朱庆璋,译.北京:人民邮电出版社,1987.
[3]王利军,郭建明,郝晶.多径效应对雷达探测低空巡航导弹的影响[J].雷达科学与技术,2010,8(1):7-10,14.
WANG Lijun,GUO Jianming,HAO Jing.The Influence of Multi-Path Effect on Low Altitude Cruise Missile Detection in Radar[J].Radar Science and Technology,2010,8(1):7-10,14.(in Chinese)
[4]张瑜,房少娟,李雪萍.低角雷达多径误差抑制的盲分离方法[J].电光与控制,2011,18(10):32-34.
[5]孙洪,安黄彬.一种基于盲源分离的雷达信号分选方法[J].现代雷达,2006,28(3):47-50.
[6]史建峰,王可人.基于循环互相关的LFM多径时延和衰减因子估计[J].电子信息对抗技术,2006,21(2):15-18.
[7]李世平,陈方超,王隆,等.多径信道下基于循环谱特征的调制识别算法[J].计算机应用,2012,32(8):2123-2127.
[8]张贤达.矩阵分析与应用[M].2版.北京:清华大学出版社,2013.
[9]李峰,郭毅.压缩感知浅析[M].北京:科学出版社,2015.
[10]GHAHREMANI M,GHASSEMIAN H.Remote Sensing Image Fusion Using Ripplet Transform and Compressed Sensing[J].IEEE Geoscience and Remote Sensing Letters,2015,12(3):502-506.
[11]雷莉霞,张跃进,黄德昌.基于压缩感知的医学图像采样新方法研究[J].CT理论与应用研究,2014,35(11):3898-3902.
[12]杨挺,武金成,袁博.谐波和间谐波检测的压缩感知恢复算法[J].中国电机工程学报,2015,35(21):5475-5482.
[13]BARANIUK R,DAVENPORT M A,DUARTE M F,et al.An Introduction to Compressive Sensing[M].Houston,TX:OpenStax CNX,2011.
[14]李少东,杨军,陈文峰,等.基于压缩感知的雷达成像技术与应用研究进展[J].电子与信息学报,2016,38(2):495-508.
[15]CANDES E J,TAO T.Decoding by Linear Programming[J].IEEE Trans on Information Theory,2005,51(12):4203-4215.
[16]王建英,尹忠科,张春梅.信号与图像的稀疏分解及初步应用[M].成都:西南交通大学出版社,2006.[17]CHEN S S,DONOHO D L,SAUNDERS M A.Atomic Decomposition by Basis Pursuit[J].SIAM Review,2001,43(1):129-159.
[18]WANG C,LIU Q,YANG X.Convergence Properties of Nonmonotone Spectral Projected Gradient Methods[J].Journal of Computation and Applied Mathematics,2005,182(1):51-56.

