自适应副瓣对消与动目标检测的联合使用∗

(空军预警学院重点实验室,湖北武汉430019)

0 引言

自适应副瓣对消(ASLC)作为空域对抗有源干扰的有效方法,最早是由Howells提出的[1],由一个高增益的主天线和一个辅助天线组成。后来,辅助天线由一个发展为多个,辅助通道加权值的计算也由简单的闭环算法演变成采样矩阵求逆算法(SMI)[2]。目前自适应副瓣对消理论上已基本成熟,并广泛地运用于实际工程中。近年来,对ASLC的研究主要集中于解决工程使用中遇到的问题。文献[3]分析了幅相误差和阵元互耦对自适应处理性能的影响及解决方法。文献[4]分析了频带不一致性对自适应处理性能的影响及解决方法。文献[5]研究了稀布阵雷达长相干积累下ASLC技术的应用。Sedivy对在超高频波段和X波段的两部雷达的ASLC系统性能进行了检测和评估[6]。更进一步,借鉴ASLC干扰对消的思想,文献[7-8]提出了和差及辅助波束联合对消来提高雷达抗主瓣干扰能力。

众所周知,雷达探测过程中,接收到的回波信号不可避免地混杂着来自地面或云、雨等的杂波信号。当杂波达到一定强度时,较弱的目标将无法探测到,雷达工作陷入被动状态。因此,产生了抑制固定杂波方法,即动目标显示(MTI)和动目标检测(MTD)[9]。当目标速度较低或运动方向在雷达探测切线方向时,MTI很难捕捉到目标,MTD弥补了这方面的不足。现代电子作战环境十分复杂,干扰和杂波总是复合存在。因而,同时使用ASLC和MTD(或MTI)来对抗有源干扰和无源杂波已经成为现代雷达的一个重要手段。目前,在雷达实际应用中,通常先采用ASLC抑制有源干扰,再采用MTD处理无源杂波,然后进行目标检测并提取目标回波。但这种先ASLC后MTD的处理方式往往导致杂波对消不彻底,甚至出现较大剩余,从而对目标检测性能产生影响。这实际上是自适应副瓣对消和动目标检测联合使用的兼容性问题,文献[10]研究了这种影响的内在原因,但并未给出有效的解决方法。文献[5]研究了对角加载对自适应权值进行约束的解决方法,但对加载值的选取没有深入研究。除此之外,鲜有公开文献深入研究该问题的有效解决方法。

1 ASLC对MTD性能的影响分析

MTD是靠不同重复周期间的杂波回波进行相消。而对于ASLC,它在每个周期对辅助天线的加权值都是变化的,变化的权值会降低MTD的杂波对消性能。ASLC处理过程中生成的加权值之所以不会保持一定值,主要是因为选用有限的快拍数据进行求权导致的误差。下面对此进行分析。

经过ASLC处理后的自适应方向图为

式中,Fm(θ),Fa分别为主天线静态方向图、辅助天线方向图,辅助天线加权值为W=[w2,w2,…,wN]T,N为阵元个数。

由Fa=[Fa1,Fa2,…,FaN]T,有

辅助天线初始增益相等,即Fa1=Fa2=…=FaN=Fa,则

选取一段快拍数据,快拍数为M,计算估计量^Rx和^rxd,即

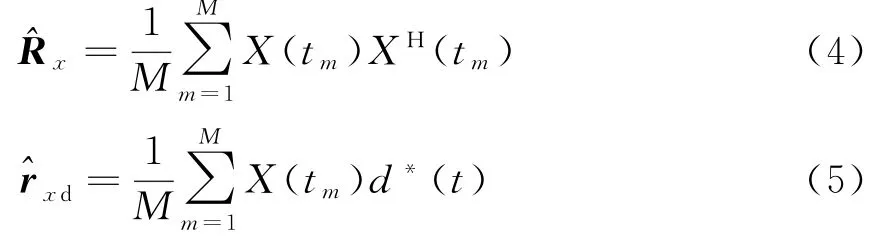
求得权值估计量为^W=^R-1xx^rxd,理想权值为Wopt,则产生误差为

即权值噪声,这种误差是计算Rx和rxd时由噪声、估计误差等产生的。

由于自适应权产生了误差,回波信号会相继发生改变,误差为

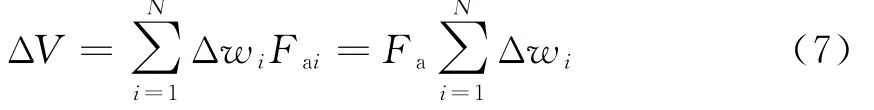
则功率误差为

由权值计算带来的误差是由有限快拍数据造成的,因而不同周期间的相关性不大,而MTD是利用相邻周期间回波相关性来进行对消,所以MTD对权值噪声无明显的对消作用。

下面给出一个仿真,为便于定量分析,仿真中用一个强固定回波来模拟地杂波,该杂波位于60 km处,脉冲压缩后强度为80 d B,并假设在150 km处有一目标,脉冲压缩后强度为20 dB。仿真环境及具体参数设置如表1所示。

表1 仿真环境及参数

图1为回波信号经脉压处理后的输出,可看出目标信号(约10 dB)完全淹没于干扰(约36 d B)中,在60 km处有1个强固定回波(约80 dB)。图2为MTD处理后16个多普勒滤波器的输出。从图中可以看出,干扰信号已被抑制,目标信号清晰出现,MTD处理后目标强度约为20 dB(第1,2号滤波器)。但是,强固定回波并没有被完全抑制,有约30 d B的剩余,这个剩余是ASLC处理所导致的权值噪声引起的,如果不加以解决,将大大降低系统对无源杂波的抑制能力。

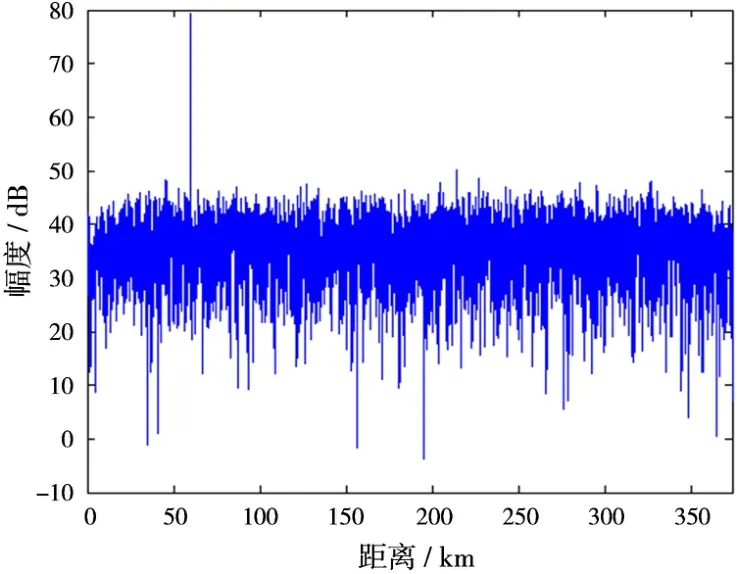
图1 脉压后的输出回波信号

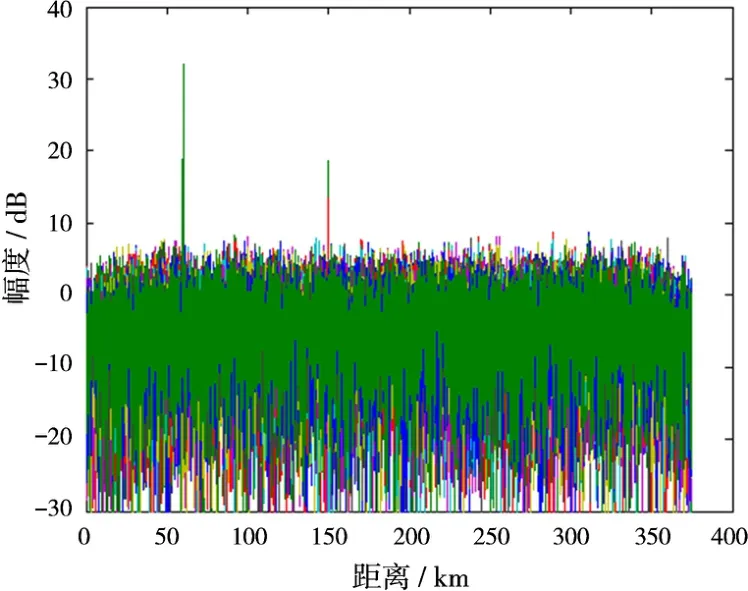
图2 MTD后输出(16个多普勒滤波器)

2 ASLC对MTD性能影响的解决方法

针对上述问题,本文提出3种解决思路:在一个相参处理间隔(CPI)内自适应权不变、对角加载、MTD前置处理。

2.1 在一个CPI内自适应权不变

在一个CPI内只进行1个重复周期的ASLC权值计算,再把该自适应权值用于CPI内所有数据进行干扰对消。这样可使CPI各个重复周期间的自适应干扰对消权值不变,消除了权值噪声,即消除了杂波谱展宽,从而不影响MTD处理对杂波的抑制性能。但是,这种处理方法会降低ASLC抑制干扰性能,下面就其具体原因展开分析。

当主天线波束不扫描时,上述方法不存在问题。但是,当波束扫描时,干扰与主天线的相对位置将发生变化,当变化较明显时,干扰位置将移出自适应零点,使得干扰不能被有效抑制。以天线6 r/min(即36°/s)为例进行分析,假设雷达重复周期为2.5 ms,MTD点数为16,ASLC权值在第8个重复周期计算,则第k个重复周期时干扰位置与自适应零点的角度间隔为

显然,干扰位置与自适应零点越远,干扰对消能力越差,下面的仿真结果说明了这种影响。

仿真1:仿真环境及参数设置同表1参数一致。

图3给出了第8,10,14和16个重复周期的干扰对消输出结果(在MTD处理前),可看出由于ASLC权值是在第8个重复周期计算得出,故该重复周期的干扰对消结果很理想,而其他3个重复周期的干扰对消很不彻底,干扰对消性能严重下降。

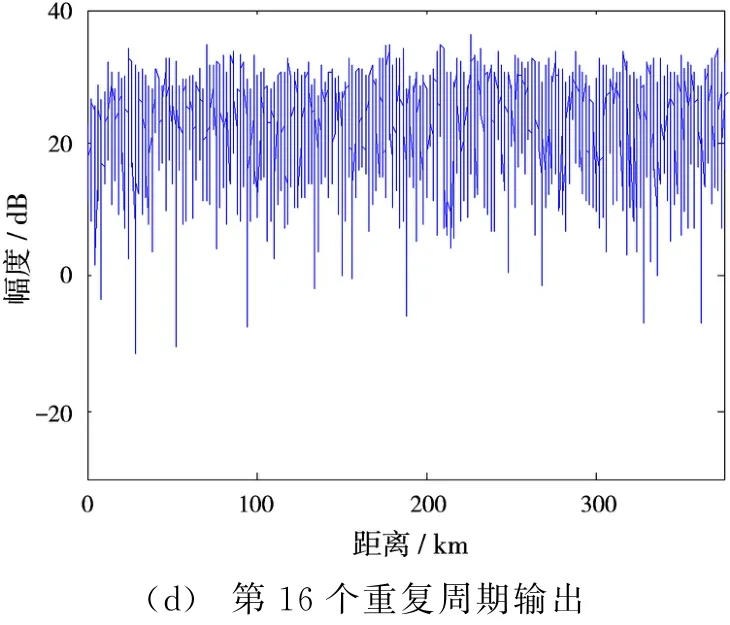
图3 多个重复周期的干扰对消输出

因此,这种方案仅适用于一个CPI内天线波束不扫描的情况(例如方位相扫体制相控阵雷达),对于方位机扫体制,并不适用。

2.2 对角加载

在计算权值时,理想权值Wopt=R-1xxrxd,则计算自相关矩阵量Rxx和相关矩阵量rxd,即

而在实际计算中,采用了采样矩阵求逆(SMI)算法,用有限次快拍数据计算估计量^Rx和^rxd(见式(4)和式(5)),以代替理想值Rx和rxd。

假设^Rx为N阶矩阵,其特征值为λk(k=1,2,…,N),对应的特征向量为μk(k=1,2,…,N)。矩阵^Rx特征分解可表示为

假定有p个干扰,则特征值中相应有p个大特征值,N-p个小特征值。理想条件下,将特征值排序为

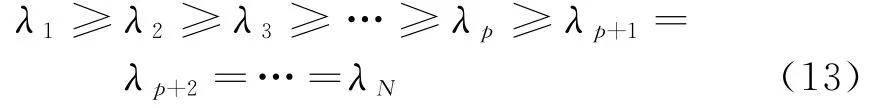
而在实际情况中,选取有限的样本数据进行计算。有限的快拍数使得^Rx的小特征值发生抖动,λp+1,λp+2,…,λN不能完全相等,进而求得的权值也有误差。因此,提出利用对角加载[11]来减轻权值噪声的影响,对角加载的实现比较简单,自适应求权如下式:

式中,I为单位矩阵,L为对角加载量。

对角加载后的^Rx小特征值抖动就会相对变小,其分散程度降低,权值误差的影响减小,ASLC性能得到优化,从而保证M TD处理对杂波的抑制性能。

对角加载量L的选取非常关键,过小则不能保证消除权值噪声的影响,过大则会降低干扰抑制能力。下面通过详细的仿真来进行分析。

仿真2:仿真参数同仿真1,考察不同对角加载量L对性能的影响。

图4是对角加载因子分别为3,10,16和30 dB时MTD处理后16个多普勒滤波器的输出。从图中可以看出,当L=3 dB和10 dB时,强固定回波仍有剩余,但明显小于无对角加载情况(如图2所示),而当L=16 dB和30 dB时,强固定回波已完全被对消,也即当对角加载因子取16 d B及以上时,基本消除了常规ASLC处理引起的权值噪声影响,使得后续MTD处理可达到80 d B的地杂波抑制能力。另外,在本仿真条件下,当L=3,10,16 d B时,ASLC处理对干扰的抑制能力基本没有下降,但是当L=30 d B时,对干扰的抑制能力约下降了4 dB,图4(d)显示剩余噪声电平抬高了4 dB,这说明30 d B的加载量过大。因此,要使得后续MTD处理达到80 dB以上的地杂波抑制能力,对角加载量L取16 dB比较合适。

图4 不同对角加载因子下MTD后输出(16个多普勒滤波器)

2.3 MTD前置处理

这种方法是脉压后先进行MTD处理抑制无源杂波,再对每个多普勒滤波器进行ASLC处理抑制干扰。由于MTD处理在ASLC前进行,因此不存在前面所述的权值噪声,所以MTD处理对无源杂波的抑制能力不受影响,同时也不会影响后续ASLC的处理性能。

下面也给出性能仿真,仿真中信号处理流程为先脉压,再MTD处理,最后副瓣对消。其他仿真环境及参数同仿真1。

仿真3:图5(a)为脉压后输出回波信号,目标淹没于干扰中;图5(b)为先经MTD再经ASLC处理后的输出。从图中可以看出,无源强杂波和有源强干扰均被完全抑制,目标可被成功检测。

从上述分析和仿真可以看出,在雷达进行方位机扫时,第一种方法不能同时有效抑制无源强杂波和有源干扰,而第二、三种方法则较好地解决了这个问题。

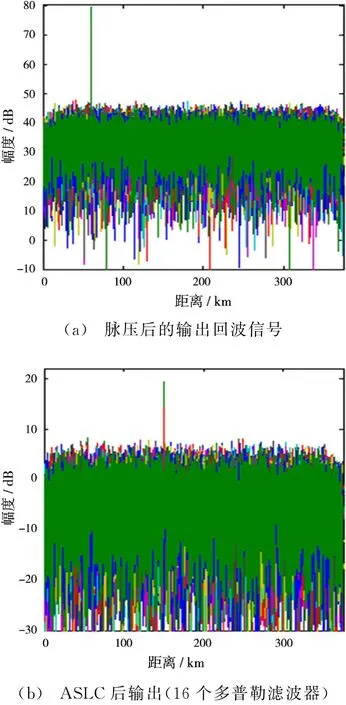
图5 干扰强度为36 dB(脉压后)时的输出结果

3 结束语

自适应副瓣对消处理会产生权值噪声,从而使得MTD抑制杂波的性能恶化。为此,本文提出3种解决方法:在一个CPI内自适应权不变、对角加载、MTD前置处理。

第一种方法适用于一个CPI内天线波束不扫描的情况,对于方位机扫体制,干扰对消很不彻底;第二种方法实现简单,增加的额外运算量几乎可忽略不计,对角加载量的选取是方法的关键,合适的加载量可使MTD保持很高杂波抑制性能;第三种方法解决最为彻底,由于不存在权值噪声,可完全同时抑制无源杂波和有源干扰。但是,该方法增加的运算量最大,所增的运算量主要是辅助通道需要进行MTD处理所致。在实际工程应用中,可根据不同应用需要对这3种方法加以选择。

[1]HOWELLS P W.Intermediate Frequency Sidelobe Canceller:US 3202990[P].1965-08-24[2015-10-16].

[2]JOHNSON J R,FENN A J,AUMANN H M,et al.An Experimental Adaptive Nulling Receiver Utilizing the Sample Matrix Inversion Algorithm with Channel Equalization[J].IEEE Trans on Microwave Theory and Techniques,1991,39(5):798-808.

[3]王永良,丁前军,李荣锋.自适应阵列处理[M].北京:清华大学出版社,2009.

[4]王峰,傅有光,孟兵,等.基于傅里叶变换的雷达通道均衡算法性能分析及改进 [J].电子学报,2006,34(9):1677-1680.

WANG Feng,FU Youguang,MENG Bing,et al.Performance Analysis and Improvement of the Equalization Algorithm Based on Fourier Transform for Radar Channel[J].Acta Electronica Sinica,2006,34(9):1677-1680.(in Chinese)

[5]陆鹏程,徐晋,关堂新,等.稀布阵雷达长相干积累下的干扰抑制设计[J].雷达科学与技术,2012,10(4):387-390.

LU Pengcheng,XU Jin,GUAN Tangxin,et al.Interference Suppression of SIAR Based on Measured Data[J].Radar Science and Technology,2012,10(4):387-390.(in Chinese)

[6]SEDIVY P.Radar Sidelobe Canceller Performance Evaluation[C]∥Conference on Microwave Techniques,Pardubice:IEEE,2013:186-189.

[7]LI Rongfeng,RAO Can,DAI Lingyan,et al.Combining Sum-Difference and Auxiliary Beams for Adaptive Monopulse in Jamming[J].Journal of Systems Engineering and Electronics,2013,24(3):372-381.

[8]周必雷,李荣锋,戴凌燕,等.子阵级和差及辅助波束联合自适应单脉冲方法[J].雷达科学与技术,2014,12(4):379-388.

ZHOU Bilei,LI Rongfeng,DAI Lingyan,et al.Adaptive Monopulse Algorithm Based on Combining Sum-Difference and Auxiliary Beams for Aoti-Jamming at Subarray Level[J].Radar Science and Technology,2014,12(4):379-388.(in Chinese)

[9]王小谟,张光义,王德纯,等.雷达与探测:信息化战争的火眼金睛[M].2版.北京:国防工业出版社,2008.

[10]孙晓兵,张守宏.数字旁瓣相消与动目标显示的兼容性分析[J].现代雷达,1992,14(5):50-56.

[11]Carlson B D.Covariance Matrix Estimation Errors and Diagonal Loading in Adaptive Arrays[J].IEEE Trans on Aerospace and Electronic Systems,1988,24(4):397-401.