基于Origin8.0的学生形成性评价——以学生成绩为样本

郑 琦　吴先球

(华南师范大学物理与电信工程学院　 广东 广州　510006)

基于Origin8.0的学生形成性评价
——以学生成绩为样本

郑 琦吴先球

(华南师范大学物理与电信工程学院 广东 广州510006)

摘 要：现阶段，成绩仍然是评价学生的主要手段．然而，由于不同测验的信度不尽相同，其成绩不能很好的反应学生现状、发展状况和潜力．本文利用Origin软件高效地进行成绩统计和转化，图式化结果并进行分析，克服原始分数的缺陷，促进学生的形成性评价．

关键词：形成性评价成绩分析Origin软件

1引言

形成性评价是在教学过程中为了获得有关教学的反馈信息，改进教学，使学生知识达到掌握程度所进行的系统性评价，即为了促进学生尚未掌握的内容进行评价[1，2]．成绩作为现阶段评价学生的主要手段，有效利用阶段性测验，可以激发学生改进动机、诊断学生的表现并以建设性的方式向学生反馈评价信息、帮助学生实施改进行动，发挥形成性评价的作用[3]．

然而，不存在完美的测验和参量完全相同的测验．测验本身由于各种原因会引起误差，比如选择题的猜测成分引起的不稳定性、测验难度、文字表达、测验长度、测验时间和评分标准等因素[4]．这些都使得代表不同测验成绩的数值不能进行比较，任一数值也不能准确地反应学生的发展水平．为克服以上不足，很多学者倡导引入标准分数对成绩进行转换．然而，教师工作繁忙，标准分数转化过程复杂，缺少有力的统计工具，使得这一倡导难以贯彻到平时的测验中[5]．

当前最常用的成绩统计工具是Excel．然而Excel的统计功能有限，标准分数转化过程复杂，图式化呈现方式有限，不能很好地进行分数统计和分析．本文将利用Origin软件高效地进行成绩统计和分析，标准分数转换，并引入标准误差，多层次图式化结果，有效地促进学生的形成性评价．

2Origin介绍

Origin是一款专业的数据分析、科技绘图软件．它采用面向对象的窗口菜单和工具栏操作，简单易学；用计划管理器管理项目，各子窗口可以单独保存、批量处理且调用便利．因此，Origin尤其适用于大量数据的快速处理和绘图．

本文主要利用了工作表窗口提供的数据计算、统计等相关的功能．利用了内置的LabTalk语言编程进行的简单编译功能．利用了绘图窗口提供的数学运算、曲线拟合以及多种二位模版进行绘图和组合对比．利用“Tools工具栏”，还能对图形数据进行精确读取．

以上只是Origin强大功能的冰山一角．此外，除Origin自带60余种二维和三维绘图模版，用户还可自定义数学函数、图形样式和绘图模版，满足不同需要．假设检验和方差分析也常用于数据统计中的比较样本差异性和寻找事物影响因素．总之，有效利用Origin，进行深入分析和处理数据，并用丰富的图形表征功能表达结果，有利于教育测量和评价[6]．

3成绩分析的理论基础

3.1标准分数

标准分数z是原始分数与平均分的离差以标准差为单位的分数，用公式表示为

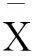
Z=50+10z

如此将分数标准化成通用的标准量表，以便进行不同考试的成绩比较．

3.2标准误差

标准误差就是测量的标准差，用Se表示

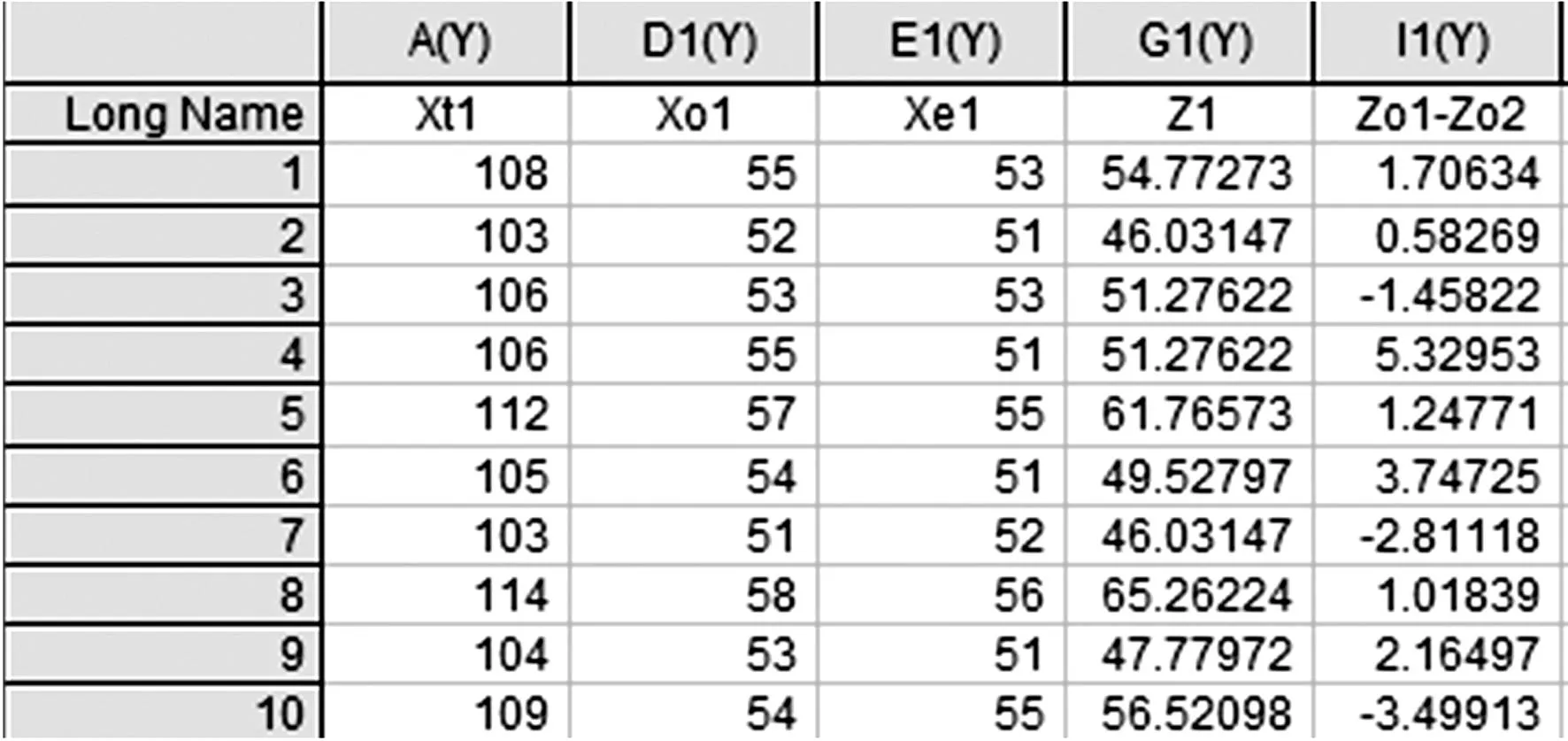
式中rtt是测量的信度，信度是对测量一致性程度的估计．如前文所述，这里主要考虑测验本身引起的误差对信度的影响．在有条件的学校，使用读卡器读取全年级学生选择题答案并做出统计，得出选择题信度rtt．粗略将选择题信度等同于整份试卷的信度，求出某次测验的标准误差Se．对于绝大多数学校，可以用分半相关法估计Se．以一个班的成绩为常模，将某次测验分为奇数项目和偶数项目(两个项目的分值要一样)．一次测验中不同题目要测的能力应具有一定的相关性，如果奇数项目得分Xo与偶数项目得分Xe一致性程度高，可以认为这个测验的信度高，那么标准误差就小；反之亦然．用分半测验分数间差异的标准差作为标准误差，如下公式

Se=SXo-Xe

其中SXo-Xe是奇数项得分与偶数项之差的标准差．

在正态分布的前提下，Xt表示实际得到的测验成绩；X∞表示真分数，真分数是理想条件下使用完备的测验工具获得的、不存在误差的成绩，可以精确地反映学生的学业水平．如果选用95%的可靠度要求，真分数将有95%的可能性落在Xt±1.96Se的范围．即

P(Xt-1.96 Se

标准误差用于对个人真分数做置信区间的估计．也就是说，不能将测验实得分数看作一个确切的点，而是具有一定的分布范围的或是带状的，是真分数的估计值．实得分数对真分数估计的如何精确可以由Se显示出来．Se越大，测验越不精确，对真分数估计的精确度就越低．这样，即可避免对两次测验之间小的差别做过分的解释[4]．这里，应用的是标准分数的标准误差．

4单科多次测试成绩分析实例

本节以广州某高中某班52名学生4次数学测试成绩为样本进行分析．将成绩进行标准分数转换，展现每次测试成绩整体分布情况、最高分和最低分、平均分、排名25%，50%，75%的分数，评估试卷质量．同时展现某学生4次测试的变化情况，引入标准误差，更有针对性和建设性地分析学生的学习状态和学习过程，制定学习方法，改进教学方法，并对接下来的学习进行预测，设定合理的目标．学生进行自我比较，可以减轻同学间比较带来的压力，改进学习动机．

4.1导入Excel数据

通过菜单命令【File】→【OpenExcel】导入Excel文件，选择OpenasOriginWorkship，得到Origin工作表．工作表中记录了4次测试成绩，以及每次测试单数项目和偶数项目成绩．

4.2标准分数转化并引入标准误差

为了统计方便，我们编辑公式计算标准分数和标准分数的标准误差，之后每次需要时就可以直接调用公式．通过菜单命令【View】→【CodeBuilder】，打开OriginC的编辑窗口．在文件目录中新建Z函数，写入程序，编译后保存．我们用同样的方法编译标准分数的标准误差公式．

选择某一列数据，通过菜单命令【Statistics】→【DescriptiveStatistics】→【StatisticsonColumns】，统计出此列数据的平均值、标准差等数据．利用Origin的计算功能，调用已编译的函数，得到每次考试的标准分数Z，奇数项与偶数项标准分数之差Zo-Ze．图1为一次测试的成绩工作表．

在新的数据表格中，记录同学甲几次考试的标准分数Za和1.96倍的标准分数的标准误差1.96 Se．

图1　成绩工作表截图

4.3图式化结果

首先进行总体统计．选中标准分数列数据，通过菜单命令【Plot】→【Statistic】→【BoxChart】，系统将自动生成箱状图．再图式化个体成绩．通过【NewLayers(Axes)】新建图层．将Za列数据进行线性拟合，并将1.96Se列数据作为误差棒插入图中．

如图2所示，以第一次考试的标准分数Z1为例：最低分和最高分的数据用“×”标示；排名1%和第99%两端分别用“短横线”标示；排名25%，50%，75%用“长横线”标示，并组成一个方框；平分分用小“□”标示．折线图的拐点是同学甲每次考试的标准分数，误差棒的长度是两倍的1.96Se，表示同学甲的成绩有95%的可能性落在误差棒所示的范围内．

图2　纵向对比不同测试成绩

4.4试卷评估与学生评价

4.4.1试卷评估

好的测试应该能很好地反映出学生的能力，有很好的区分度，其成绩服从正态分布．如图2，第1次测试Z1和第4次测试Z4成绩平均分(小“□”标示)和排名中位数学生的成绩(方框中的长横线)接近，整体分布接近于常态分布，说明试题难度、区分度等设置较为合理．第2次测试Z2和第3次测试Z3平均分都明显低于排名中位数学生的成绩，成绩分布为偏常态的，高分段学生较多，试题有待改进．

4.4.2学生评价

同学甲4次测试的原始分分别为：108，118，130，82，呈先上升，最后一次下降趋势，受试题影响不能反映学生真实情况．转换为标准分数，成绩分别为：54.77，60.63，59.11，47.78，由图2折线图标示，呈先上升，第3次考试开始下降趋势．

具体到每次考试，引入标准误差(误差棒标示)分析．这里，可以将误差棒理解为学生测试成绩的浮动范围．如图2，以第3，4次考试为例，第4次测试的误差棒最高端(可能达到的最高分)仍低于第3次测试误差棒最低端，说明第4次测试较第3次有明显退步．然而，第3次测试分数虽然低于第2次测试分数，但第3次测试可能最高分(误差棒最高端)高于测试2的分数，说明第3次测试成绩较第2次没有明显改变．同理，第2次测试误差棒的最低端略高于第1次测试的分数，说明第2次测试较第1次有略微进步．

由此反馈信息，同学甲此阶段数学成绩先略微上升后保持不变，又明显下降，总体呈下降趋势．接下来，需要进行更有针对性的反思总结，做出预测，制定目标．

5多科多次测试成绩分析实例

本节以同学乙语文、英语、数学3科4次测试的成绩为样本进行分析．通过建立彩色气泡图，比较4次测验3科目的成绩，更全面地考虑学生的发展情况，进一步完善形成性评价．

5.1图式化表示

建立工作表记录同学乙4次测验中语文、英语和数学的标准分数Za和1.96倍的标准分数的标准误差1.96Se．通过菜单命令【Plot】→【Symbol】→【Bubble+ColorMapped】，生成彩色气泡图[7]．

如图3所示，红色气泡纵向代表语文测试标准分数范围，绿色气泡纵向代表英语测试标准分数范围，蓝色气泡纵向代表数学测试标准分数范围．折线图拐点是每次测试的标准分数．

图3　纵横向对比不同科目成绩

5.2学生评价

首先单科目分析．对于语文测试，前3次都无明显变化，第4次测试较第1次和第3次测试有略微下降，总体有略微下降趋势；对于英语测试，第1，2次和3，4次测试无明显变化，第3次测试较第2次略微下降，第4次测试较第1次略微下降，总体有略微下降趋势；数学测试变化明显，除了第1，2次无明显变化，第2，3次进步明显，3，4次也有略微进步，总体进步明显．

再总体比较不同科目，同学乙一开始偏科严重，语文和英语都明显优于数学，但随着数学的明显进步，现在已无偏科现象．可见同学乙虽然数学基础不好，但潜力很大；也要考虑，语文和英语的略微下降，是否因为学生用了太多的时间学习数学？下一步，如何合理安排时间精力分配，使同学乙全面发展是值得思索的．

6结语

本文利用Origin强大的统计、计算和作图功能，对测试成绩进行统计、转换、图式化．整体分析成绩分布，个体分析成绩状况；纵向分析成绩发展，横向对比不同科目成绩，有助于学生的形成性评价．Origin内嵌Excel工作簿，基于模版操作，容易上手，便于广大教师使用．

参 考 文 献

1恩斯特·卡西尔.人论.北京：光明日报出版社,2008

2亓文涛,乔爱玲.形成性评价在基础教育教学中的应用研究.现代教育技术,2007(11):89～92

3王宙.普通高校形成性学生评价研究.上海：华东师范大学，2007

4戴忠恒.心理与教育测量.上海：华东师范大学出版社,1987

5王小燕.MSExcel数据分析在成绩分析暨试卷质量评估的应用.现代教育技术,2010(10)：135～137

6吴先球,高远静,卢炜杰.Origin软件在考试数据分析与评价中的应用.教育测量与评价,2014(5)：4～7

7方安平,叶卫平,Origin8.0实用指南.北京：机械工业出版社，2012

Student's Formative Assessment based on Origin8.0

Zheng QiWu Xianqiu

(South China Normal University Physics & Telecomunication Engineering College,Guangzhou,Guangdong510006)

Abstract:At this stage, test scores are still the main means to evaluate students. However, the reliabilities of each test are different, the scores can not represent students' present ability, development status and potential effectively.The scores can be statistically analyzed and transformed by Origin software, the results can be schematized and assessed by graphs, to overcome the defects of the original scores, to promote the formation of students' evaluation.

Keywords:formative evaluation;score analysis;Origin software.

收稿日期：(2015-04-26)