光纤损耗对孤子系统传输的影响
徐 丹 萨茹拉
(内蒙古师范大学物理与电子信息学院 内蒙古 呼和浩特 010021)
光纤损耗对孤子系统传输的影响
徐 丹萨茹拉
(内蒙古师范大学物理与电子信息学院内蒙古 呼和浩特010021)
摘 要:利用分步傅立叶法数值求解了包含光纤损耗效应的非线性薛定谔方程,分别仿真模拟了其对亮孤子和暗孤子脉冲在各向同性光纤中传输特性的影响.结果表明,随着传输距离的增大,光纤损耗导致基阶亮孤子和暗孤子的峰值功率减小,脉冲加速展宽.而对于高阶孤子,光纤损耗会破坏高阶亮孤子的周期性变化,但对于高阶暗孤子的影响几乎与基阶暗孤子相同.因此在光纤损耗参数相同的情况下,暗孤子的相对衰减率比亮孤子的相对衰减率小,故暗孤子比亮孤子更稳定.
关键词:光纤损耗光孤子相对衰减率
1引 言
光脉冲在光纤中传输时,若群速度色散效应(GVD)与自相位调制效应(SPM)平衡,即可形成光孤子.光孤子可以在光纤中实现无畸变传输,这对光纤通信有重要意义[1~3].光纤损耗是光纤的传输特性之一[4,5],在孤子通信系统中可以不用中继站,而正是由于光纤损耗的存在,必须对光纤损耗进行增益补偿[6],才可把光信号无畸变地传输极远距离.有关损耗对孤子通信系统的相关研究,从20世纪70年代起有所关注[7~9],最近相关作者[10]研究了内部具有分段纤芯和凹陷包层结构的超低损耗光纤(ULL),其损耗在1.55 μm处可降低至0.18 dB/km,这接近光纤损耗的理论极限.关于光孤子的传输特性绝大多数是在忽略光纤损耗的情况下进行的,近些年,Kurokawa研究了色散管理孤子在超低损耗光纤中的传输特性[11],而有关于光纤损耗对孤子(亮孤子和暗孤子)系统传输特性的文章较少.
本文利用分布傅立叶法[12]数值求解了考虑光纤损耗效应后,光孤子在各向同性介质中传输时所满足的非线性薛定谔方程,分别仿真模拟了光纤损耗对亮孤子和暗孤子传输特性的影响.结果表明,在光纤损耗参数相同的情况下,暗孤子比亮孤子更稳定.
2理论模型
在考虑光纤损耗的情况下,光孤子在各向同性介质中传输时,其慢变包络振幅A所满足的非线性薛定谔方程为[12~17]
(1)

采用分布傅立叶法对式(1)进行数值求解,现将式(1)改写为如下形式

(2)

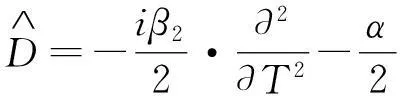
(3)

(4)
光脉冲在光纤中传输时,色散作用和非线性作用是同时存在的,为了简化问题,分布傅里叶法中假设光脉冲在光纤中传输时,光场在一小段长度h内受到色散作用和非线性作用是独立的,进而得出一个近似结果,因为h非常小,所以在误差要求的范围内,这个结果可以认为是较为精确的结果[17].其具体过程为:光脉冲在z到z+h这一小段距离内传输时,分两步走.下面对式(3)和式(4)分别进行求解,得出线性算符和非线性算符.利用MATLAB软件计算线性算符和非线性算符以及脉冲传输过程中的具体数值,并进行曲线仿真.
3数值模拟讨论与分析
现输入亮孤子和暗孤子脉冲,其表达式分别为
A1(0,T)=Nsech(T)
(5)
A2(0,T)=Ntanh(T)
(6)

3.1基阶孤子(N=1)

图1 考虑损耗的情况下,基阶孤子脉动冲

其中,P0为初始脉冲的峰值功率,P1为传输到一定距离处的峰值功率.由图2(a)可以计算出亮孤子传输的10z0处的衰减率d亮≈95%,而暗孤子传输到10z0处的衰减率为d暗≈83.5%.可以看出,基阶暗孤子和基阶亮孤子,当光纤中损耗参数相同时,基阶暗孤子比基阶亮孤子更稳定,其脉冲展宽速度更慢.

图2 基阶孤子的初始脉冲以及基阶孤子传输
3.2二阶孤子(N=2)
在不考虑光纤损耗的情况下,基阶孤子的GVD和SPM相互平衡,这样脉冲的形状和频谱都不发生变化.对于二阶亮孤子,在光纤中传输时,其脉冲形状遵循一种周期性[12],即脉冲形状在z=mz0(m为整数)处得到恢复.而二阶暗孤子在光纤中传输时,其在中央黑孤子两侧出现了一对灰孤子,由于群速度不同,灰孤子随着传输距离的增大而逐渐远离中央黑孤子.而考虑损耗后,如图3所示,它给出了损耗参数α=0.18 dB/km时二阶孤子在5个孤子周期内的演化过程,其中(a)、(c)为亮孤子; (b)、(d)为暗孤子.从图3(a)、(b)中可以看出,二阶亮孤子不再具有周期性,脉冲经历一个初始窄化的过程,导致其峰值加速增大到z0处达到最大值,而后加速衰减,传输到2z0处降为最小,随后脉冲又变窄故峰值功率又再次增大,传输到4z0处脉冲峰值再次达到最大值,而后不再出现周期性的变化,随传输距离增大而逐渐衰减,最终消失.而暗孤子的峰值功率随着传输距离的增大加速减小.图3(c)和(d)分别是亮孤子和暗孤子在的初始位置(实线)和传输到10z0处(虚线)的脉冲形状.可以看出在10z0处亮孤子的脉冲展宽程度要远大于中央黑孤子的展宽程度.利用之前引入的相对衰减率d,可以分别计算出亮孤子和暗孤子的相对衰减率为:d亮≈96.85%,d暗≈82.17%.从中可以看出,二阶亮孤子的相对衰减率略有增大,而二阶暗孤子的相对衰减率几乎不变.因此光纤损耗破坏了亮孤子的周期性变化,而当光纤中损耗相同时,暗孤子的衰减速度要小于亮孤子的衰减速度,其展宽程度也比亮孤子的展宽程度小,故相比之下暗孤子比亮孤子更稳定.
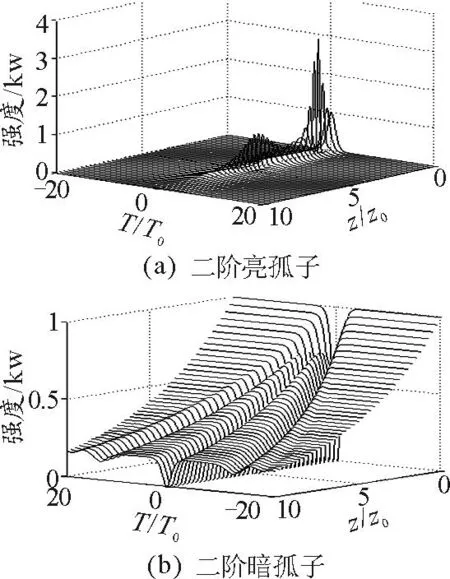

图3 在损耗情况下二阶孤子在10个
3.3三阶孤子(N=3)
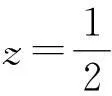


图4 在考虑损耗的情况下,三阶孤子
4结论
在考虑光纤的损耗作用的情况下,运用分步傅立叶法对光孤子的慢变包络振幅A所满足的非线性薛定谔方程进行数值求解,并分别对不同阶数的亮孤子和暗孤子的演化情形进行讨论.结果表明,基阶亮孤子和暗孤子在传输过程中,光纤损耗会导致其峰值功率减小,脉冲加速展宽,而暗孤子的相对衰减率要比亮孤子的相对衰减率小.对于高阶亮孤子和暗孤子,损耗破坏了高阶亮孤子的周期性变化;而损耗对于高阶暗孤子的影响几乎与基阶暗孤子相同.从而表现为在光纤中有损耗以及背景噪声的情况下,暗孤子比亮孤子更为稳定.
参 考 文 献图5不同孤子脉冲的相对衰减率随传输距离的变化关系
1Kompfner R 1965 Science 8 149~155
2Tsigaridas G.Polyzos I.Giannetas V. Persephonis P 2008 Chaos,Solitons & Fractals 35 151~160
3Kibeler B,Fatome J,Finot C, Millot G, Dias F, Genty G,Akhmediev N,Dudley J M 2010 Nat.Phys.6 790~795
4Mollenauer L F 2003 Science 7 996~997
5Smith C M,Venkataraman N,Gallagher M T, West J A,Borrelli N F,Allan D C,Koch K W 2003 Nature 424 657~659
6Dung J C 2005 Opt.Commun. 246 85~89
7Kapron F P,Kerk D B,and Maurer R D 1970 Appl.Phys.Lett.17 423~425
8Horiguchi M and Osanai H 1976 Electron.Lett.,12 310~312
9Miya T,Terunuma Y,Hosaka T,and Miyashita T 1979 Electron.Lett.15 106~108
10Pournoury M,Moon D S,Nazari T,Kassani S H,Do M H 2014 Opt.Commun.317 13~17
11Kurokawa K,Tajima K,Tsujikawa K,Nakajima K 2006 J.Lightwave Technol.24 32~37
12Agrawal G P 2013 Nonlinear Fiber Optics (5nd ed.)( Boston:Academic Press)
13Yu Yu, Jia Wei-Guo,Yan Qing et al.Acta Phys.Sin.,2015,64(5):054207 (in Chinese)
14Wang Mei-Jie,Jia WeiGuo,Zhang Si-Yuan et al.Acta Phys.Sin.,2015,64(3):034212(in Chinese)
15Potasek M J 1987 Opt.Lett.12,921
16Zhong X Q,Tang T T,Xiang A P 2011 Opt.Commun.284 4727
17Hook A,Karlsson M,1993 Opt.Lett.18,1388

收稿日期:(2015-02-04)
作者简介:指导教师:萨茹拉(1974-),女,副教授,主要从事理论物理的教学及研究.

