粗糙集正域在心理健康测量中的应用

粗糙集正域在心理健康测量中的应用

张燕

(陕西理工学院 数学与计算机科学学院，陕西 汉中 723001)

摘要：分析粗糙集正域的相关理论，提出一种基于粗糙集正域的决策表约简算法，用属性重要度的大小来判断属性是否被约简.通过对心理健康量表数据实例验证，该算法在约简后得到影响测量结果的重要属性，为构建更为科学、合理的测评量表提供理论依据，具有一定的实用价值.

关键词：粗糙集；正域；心理健康；属性

中图分类号：TP18文献标志码：A

文章编号：1008-5564(2015)03-0039-03

收稿日期：2015-04-05

基金项目：陕西职业技术学院校本课题项目 (Y1403)

作者简介：王红喜(1981—)，男，山西大同人，陕西职业技术学院计算机系讲师，主要从事小波分析及图像处理研究.

Application of Positive Region of Rough Sets inPsychological Health Measuring

ZHANG Yan

(School of Mathematics and Computer Science, Shaanxi University of Technology, Hanzhong 723001, China)

Abstract：A decision table reduction algorithm based on the positive region of rough set was proposed by analyzing the related theories of the positive region of rough set, and the importance of attribute was used to judge whether the attribute should be reduced. By the testing example of the mental health scale data, the algorithm can obtain more important attributes which affect the measuring results after reduction, and the algorithm has a certain practical value and provides a theoretical basis for constructing more scientific, reasonable evaluation table.

Key words：rough sets; positive region; psychological health; attribute

近年来，随着社会各界对心理健康问题越来越重视，心理测量的概念和技术也得到了推广和普及.对比较常用的心理测量量表，通常以各种情绪、人际关系、适应性等作为指标来评价[1]，从而最终判断心理健康状况.然而，每一个评价指标的重要度在评价结果中不同，甚至有些指标对评价结果影响甚微，会干扰人们作出正确而简洁的决策.所以，在不改变评价结果的基础上，尽可能少的选取评价指标，构建测评量表，可以更科学、合理的简化心理测评的过程.本文用粗糙集属性约简理论来实现心理健康量表的属性约简[2]，构建更为客观、合理的量表.

Rough集(Rough Sets，也称粗糙集)[3]理论是由波兰华沙理工大学Pawlak教授于20世纪80年代提出的一种处理含糊和不精确问题的数学工具[4].属性约简是粗糙集理论研究的核心内容之一，它是在保持知识库分类能力不变的条件下，删除其中不相关或不重要的属性.通过属性约简可以从特征信息中提取有用的信息，简化知识处理过程.人们往往期望找到具有最少条件属性的约简，即最小约简.[5]然而，已经证明了找出一个决策表最小约简是NP-hard问题.[6]

1粗糙集相关概念

粗糙集理论的研究对象是信息表[7]，通过指定对象的属性和它们的属性值来描述.

定义2在信息表S=(U，R，V，f)中，对于每个属性子集B⊆R，可以定义一个不可分辨二元关系IND(B)，IND(B)={(x,y)|(x,y)∈U2,∀b∈B(b(x)=b(y))},IND(B)是一个等价关系.

定义3设X⊆U是任一子集，R是U上的等价关系，则有

R-(X)=∪{Y∈U/R:Y⊆X}

(1)

R-(X)=∪{Y∈U/R:Y∩X≠∅}

(2)

分别称式(1)和(2)为X的R下近似和R上近似，Y是U是按等价关系R分成的等价类.X的R正区域为POSR(X)= R-(X).

在信息系统中，冗余属性的存在[10]，一方面是对资源的浪费，另一方面干扰人们做出正确而简洁的决策.人们希望找出具有最少条件属性的约简，即最小约简，核是所有约简的子集.

定义4设U为一个论域，P和Q都是U上的等价关系簇，如果POSP(Q)=U，则称论域U是P上相对于Q一致的.[11]

定义5设U为一个论域，P和Q都是U上的等价关系簇，若P的Q独立子集S⊂P有POSS(Q)=POSP(Q)，则称S为P的Q约简.

定义6决策表S=(U，R，V，f)，∀a∈C,R⊆C,定义a相对于R的属性重要度[12]为Sign=(a,R,D)=|POSR(D)|-|POSR-{a}(D)|.如果Sign=0，则属性a是相对于决策属性D不必要的，从决策表中删除属性a；如果Sign>0，则属性a是相对于决策属性D必要的，不能删除.

2基于粗糙集正域属性约简算法

输入：决策表S=(U,C∪D,V,f)，其中U是论域，C是条件属性集合，D是决策属性集合.

输出：决策表S的一个约简T.

步骤1：在决策表S=(U,C∪D,V,f)中，计算U/IND(C),U/IND(D),计算出条件属性集C相对于决策属性D的正域POSC(D).

步骤2：将条件属性集C赋值给R，R=C；T=∅；

步骤3：计算U/IND(C{ai})、正域POS(C{ai}),ai的属性重要度Sign=(ai,C,D)=|POSC(D)|-|POSC-{ai} (D)|；

步骤4：if Sign>0,T=T∪{ai},R=R-{ai+1}；

步骤5：R≠∅,转向步骤3执行，否则，输出C相对于D的一个相对约简T.

3心理健康测量实例应用

本次实验用到的数据是针对某银行40名职员的心理健康测评结果，主要测量的是受测者近期有无不健康的心理状态，其中包含9个测量因子，如表1所示.

经过对原始测评数据的预处理，删除重复的行，经过离散化，用0表示正常，1表示异常，得到如表2所示的测评数据.其中论域U={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}表示15个样本，条件属性集C={a1,a2,a3,a4,a5,a6,a7,a8,a9},决策属性集D={d}.

表1　某银行员工心理健康测量因子

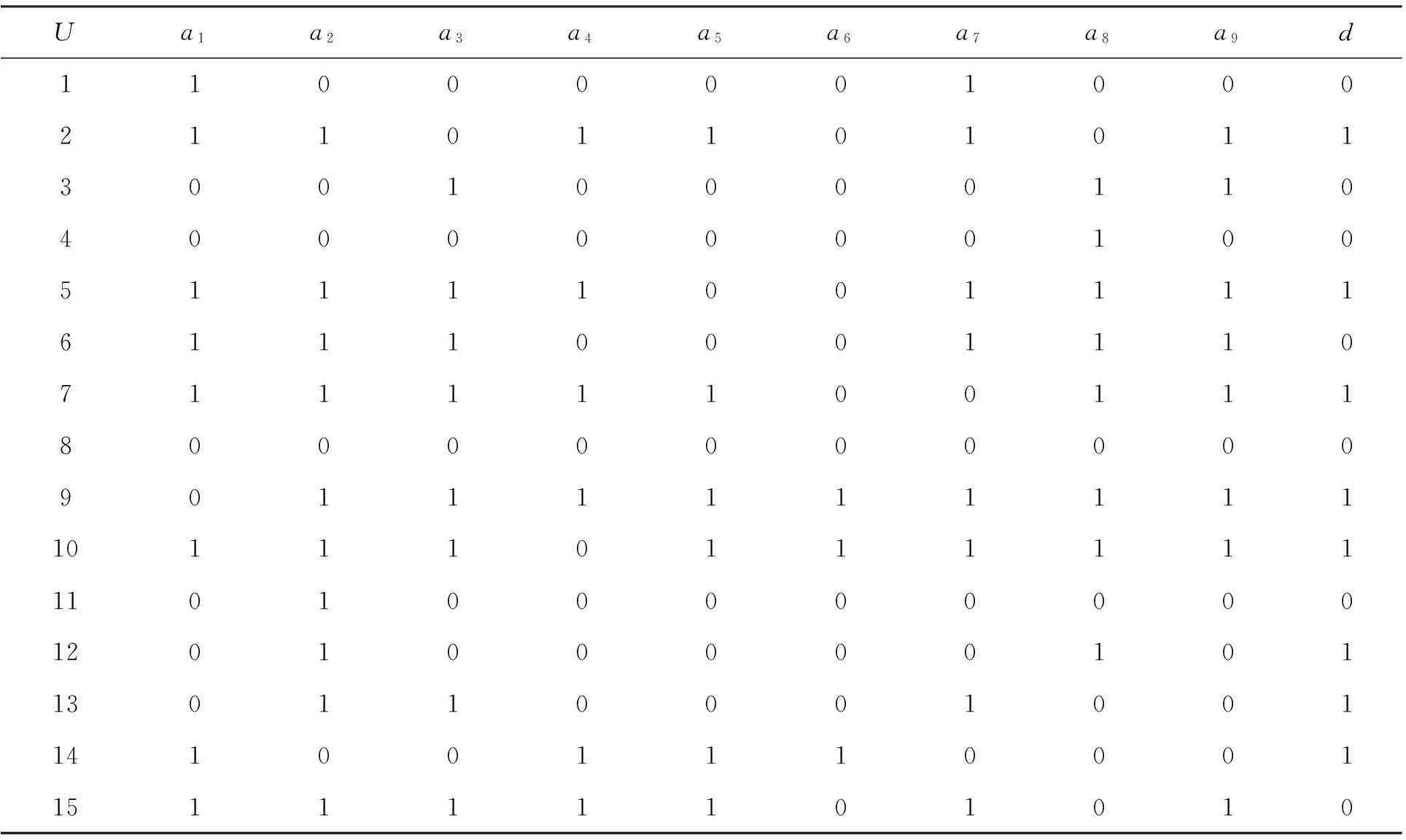
表2　银行员工心理健康症状况测评数据

根据本文运用的算法，条件属性集C对于U的等价划分为:

IND(C)={{1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11},{12},{13},{14},{15}},

决策属性集D对于U的等价划分为:IND(D)={{1,3,4,6,8,11,12,15},{2,5,7,9,10,13,14}},

POSC(D)={{1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11},{12},{13},{14},{15}}=U.

因此，论域U是C上相对于D一致的，说明该决策表是完全确定的决策表，决策表中不包含不一致信息.

计算属性a1的重要度，Sign=(a1,C,D)=|POSC(D)|- |POSC-{a1} (D)|；先从条件属性集C中去掉属性a1,得条件属性集C{a1}对于U的等价划分为：

IND(C{a1})={{1},{2},{3},{4},{5,9},{6},{7},{8},{10},{11},{12},{13},{14},{15}},

POSC-{a1} (D)= {{1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11},{12},{13},{14},{15}},

Sign=(a1,C,D)=|POSC(D)|- |POSC-{a1} (D)|=0.

同理得a2,a5,a6,a7,a9的重要度均为0，而a3、a4、a8的重要度为Sign=(a3,C,D)=2,Sign=(a4,C,D)=2,Sign=(a8,C,D)=2.

由定义5可知，属性a3、a4、a8重要度Sign大于0，相对于决策属性D必要的，不能删除，T={a3、a4、a8}是决策表的一个相对约简.

由上述粗糙集正域约简算法对心理健康测量决策表约简结果得出，受测者近期有无不健康的心理状态，主要取决于近期是否在人际交往上有不自在、不适应的问题(a3)、是否情绪不安，处于焦虑状态中(a4)、是否具有一些偏执性的思维特征，例如固执己见、多疑敏感、好斗记仇等(a8).

4结语

本文探讨了基于粗糙集正域模型下心理健康测量决策表的约简方法，通过分析粗糙集正域的相关理论，提出一种基于粗糙集正域的决策表约简算法.实验研究表明，该算法在约简后得到影响测量结果的重要属性，为构建更为科学、合理的测评量表提供理论依据，具有一定的实用价值.但是，该研究一方面还需要对现有数据进一步从多个角度来深入分析和挖掘，另一方面也需要粗糙集领域相关算法研究的支持.

[参考文献]

[1]王国胤.Rough集理论与知识获取[M].西安:西安交通大学出版社，2001.

[2]张文修，吴伟志，梁吉业，等.粗糙集理论与方法[M].北京:科学出版社，2003.

[3]刘清.Rough集及Rough推理[M].北京:科学出版社，2001.

[4]杨传健,葛浩,汪志圣.基于粗糙集的属性约简方法研究综述[J].计算机应用研究,2012,29(1)：215-219.

[5]余嘉元.粗糙集和神经网络在心理测量中的应用[J].心理学报,2008,40(8)：939-946.

[6]徐章艳,舒文豪,钱文彬,等.基于序关系的快速计算正区域核的算法[J].计算机科学,2010,37(7)：102-106.

[7]TENG S H,ZHOU S L,SUN J X,et al.Attribute reduction algorithm based on conditional entropy under incomplete information system[J].J NUDT,2010,32(1):90-94.

[8]张贤勇,熊方,莫智文,等.变精度上近似与程度下近似粗糙集模型的正域及其算法[J].计算机科学,2012,39(1)：111-115.

[9]唐朝辉，陈玉明.基于粗糙集正域的医疗决策表约简算法[J].宜春学院学报,2012,34(8)：76-80.

[10]冯林，罗芬,方丹，等.基于改进扩展正域的属性核与属性约简方法[J].山东大学学报,2012,47(1)：26-31.

[11]李洪,向永生,陈曦.一种基于正域的决策表增量求核算法[J].微计算机信息,2010,26(11)：82-85.

[12]冯林.一种扩展正域的属性约简方法[J].计算机工程,2010,36(21):62-64.

[责任编辑王新奇]

Vol.18No.3Jul.2015