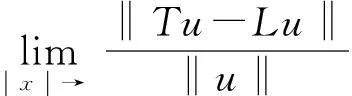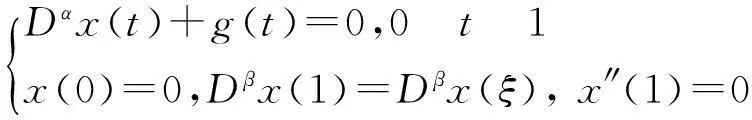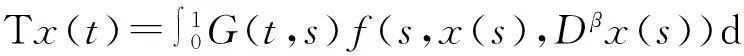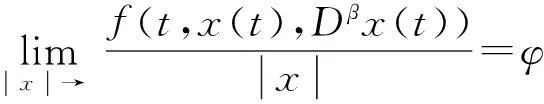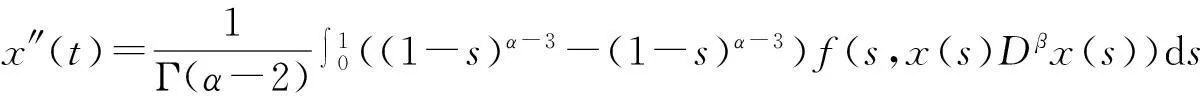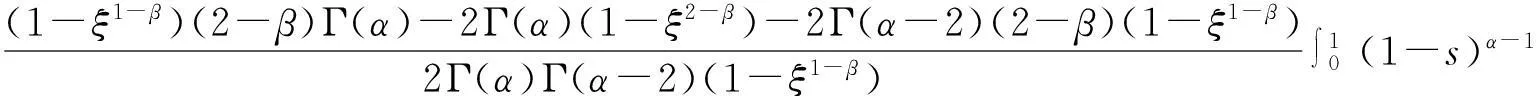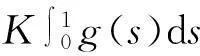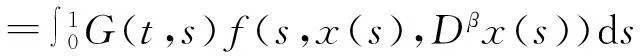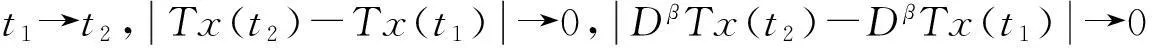一类具三点边值问题的分数阶微分方程正解的存在性
一类具三点边值问题的分数阶微分方程正解的存在性
刘小刚1,刘慧敏2
(1.西北大学 现代学院,西安 710130; 2.郑州成功财经学院 共同学科部,郑州 451200)
摘要:讨论了一类具三点边值问题的分数阶微分方程正解的存在性,给出解的存在性条件,并运用Schauder不动点定理进行讨论,推广已有的某些结论.
关键词:分数阶微分方程;边值问题;正解;不动点定理;格林函数
中图分类号:O175.8文献标志码:A
文章编号:1008-5564(2015)03-0031-04
收稿日期:2015-04-08
基金项目:西安财经学院科研
作者简介:郭妞萍(1978—),女,山西永济人,西安财经学院统计学院讲师,硕士,主要从事数值分析研究.
ExistenceofPositiveSolutionsofFractionalDifferentialEquationsforAClassofThree-pointBoundaryValueProblems
LIUXiao-gang1,LIU Hui-min2
(1.SchoolofModern,NorthwestUniversity,Xi’an710130,China; 2.DepartmentofGeneralSubjects,
ZhengzhouChenggongUniversityofFinanceandEconomics,Zhengzhou451200,China)
Abstract:In this paper, the existence of positive solutions of fractional differential equations for a class of three-point boundary value problems was discussed and the existence conditions of solutions were given. The Schauder fixed-point theorem was used to promote some existing conclusions.
Keywords:fractionaldifferentialequations;boundaryvalueproblem;positivesolution;theSchauderfixed-pointtheorem;Greenfunction.
近年来,分数阶微分方程在工程、科技、图像处理以及非线性动力系统等众多领域都有重要应用,其研究受到越来越多的关注,特别是分数阶微分方程边值问题引起了广泛的研究,一些相关专著已经出版.[1-2]
赵霞在文献[3]中利用不动点定理,给出了非线性分数阶微分方程边值问题
(1)
正解的存在性,1<α2,0<β1,0γ1,Dα是标准的Riemann-Liouville型分数阶微分.
受到此文献的启发,本文研究下面一类具三点边值问题分数阶微分方程正解的存在性:
(2)
2<α3, 0<β1,0<ξ1,Dα,DβCaputo均为Caputo微分.利用不动点定理,得到了边值问题(2)至少具有一个正解的存在性条件.
1预备知识和引理
参考文献Caputo型分数阶微分的定义见[3].

引理2[4](Banach 压缩映射原理) 设U是Banach空间X的有界闭子集,如果T:U→U满足∃0 引理4[5]设函数g∈L[0,1],则边值问题 其中: 证明对方程(2)两边同时进行α阶积分,根据边界条件很容易得到. 引理5函数G(t,s)具有以下性质: (1)G(t,s)∈C([0,1]×[0,1]); (2)对任意的t,s∈[0,1],有G(t,s)>0成立. 2主要结果 在证明主要结论前,首先给出下列假设: (H1)f:[0,1]×[0,+)×[0,+)→[0,+)关于t∈[0,1]是勒贝格可测的; (H2)f:[0,1]×[0,+)×[0,+)→[0,+)关于x∈[0,)是连续的; (H3)存在非负实值函数m(t)∈C([0,1],[0,)),使得; 下面给出本文的主要结果: 定理1设(1-ξ1-β)(2-β)Γ(α)>2Γ(α)(1-ξ2-β)+2Γ(α-2)(2-β)(1-ξ1-β), 则边值问题(2)的解x≥0. 所以函数x(t)在[0,1]是凹函数.又因为x(0)=0,并且 f(s,x(s)Dβx(s))ds≥0.因此,边值问题(2)的解x≥0. 定理2如果(H1),(H2),(H4)成立,并且0<κ<1, 接着证明算子T在E中将一个有界集映射成有界集.取Ω⊂H是一个有界集,∀x∈Ω,结合条件(H4)有 (3) (4) 因为 (5) 所以算子Tx将一个有界集映射成有界集. 最后证明算子Tx是等度连续集.对任意的x∈H,0 (6) (7) 综上所述,根据Ascoli-Arzela定理可知,T是全连续算的. 因此,根据引理2,T至少存在一个正解. 证明对任意的x,y∈H,t∈[0,1],有 (8) (9) 下证λ=1不是算子L的特征值.事实 所以,‖x‖=‖Lx‖ 根据条件(H5),∀ε>0,存在充分大的N>0,使得对任意的t∈[0,1],有 (10) (11) 根据引理3,算子T存在一个不动点. [参考文献] [1]CABADAA,WANGGT.Positivesolutionsofnonlinearfractionaldifferentialequationswithintegralboundaryvalueconditions[J].JournalofMathmaticalAnalysisandApplications,2012,389(1):403-411. [2]ZHANGYing-han,BAIZhang-bing.Existenceofsolutionsfornonlinearthree-pointboundaryvalueproblematreso-nance[J].JApplMathComput,2011,36(1/2):417-440. [3]赵霞,刘洋,胡卫敏.分数阶微分方程三点边值问题正解的存在性和唯一性[J].伊犁师范学院学报:自然科学版,2013(1):1-4. [4]ZEIDLERE.Nonlinearfunctionalanalysisanitsapplication-I:Fixed-pointtheorems[M].Springer:NewYork,NY,USA,1986. [5]ZHANGS.Positivesolutionsforboundaryvalueproblemofnonlinearfractionaldifferentialequations[J].ElectronJDifferEqu.,2006,36:1-12. [6]SAMKOSG,KILBASAA,MARICHEVOI.Fractionalintegralsandderivatives[M].GordonandBreach,Amsterdam,1993. [责任编辑王新奇] Vol.18No.3Jul.2015