混杂存在时因果效应边界的研究

混杂存在时因果效应边界的研究

马蔷，单娜

(长春工业大学 基础科学学院，吉林 长春 130012)

摘要:平均因果效应是反映总体中平均处理效果的一个常用的度量．在不可观测的混杂因素存在时，平均因果效应往往很难由直接的方法来估计．本文基于VanderWeele和Chiba的理论结果对两种边界进行比较研究，通过实例和模拟研究给出一些建议，以为实际领域的工作者进行有效的分析和使用．

关键词:平均因果效应；混杂；单调性假设；边界

DOI:10.13877/j.cnki.cn22-1284.2015.10.011

收稿日期：2015-04-18

基金项目：国家自然科学

作者简介：马蔷,女,内蒙古赤峰人,长春工业大学基础科学学院在读硕士研究生．

中图分类号：O212文献标志码：A

对于因果关系的分析，首先需要用一种数学语言来定义因果效应，最流行的方法是虚拟事实模型．假设我们可以去询问虚拟事实的问题，即对于同一个接受过“处理”的人，我们想要了解他如果没有接受“处理”会发生什么．而对于没有接受过“处理”的人，我们会产生同样的问题，如果他接受了“处理”又会发生什么．进一步，如果我们想要对受试者的全体进行研究，平均因果效应(average causal effect简称ACE)就是更好的选择．但是，很多情况下，由于道德或者时间等因素，虚拟事实的问题无法获得回答，从而平均因果效应也就无从计算[1]．

在实际问题中，平均因果效应的估计一般都是在一些假设下进行的，而混杂又常常给因果效应的估计带来许多问题．混杂因素亦称混杂因子，是指与原因和结果有关，若在研究的人群组中分布不匀，可以歪曲原因与结果之间真正联系的因素．对于混杂因素(比如年龄、性别等)可以观测的情况，平均因果效应的估计方法已有广泛的研究，比如Pearl[2-3])，Kuroki and Miyakawa[4]和耿直[5]等．但是，在很多情况下，混杂因素(比如基因)是不可观测的，因此，因果效应的估计是现代研究中的一个热点．VanderWeele[6]在关于协变量单调的假设下给出平均因果效应边界的一个表达式．Chiba[7]在VanderWeele的基础上增加了处理分配，进而研究平均因果效应的边界，但是并未研究两种方法的比较．本文是在两篇论文的理论基础上进行进一步的比较分析，通过实际例子和模拟研究给出两种边界的不同表现，从而给实际应用者提出一些建议．

1符号及理论基础

X表示一个两值的处理；X=1表示接受处理；X=0表示未接受处理；U表示一个不可测量的协变量；Z表示一个或一组可观测的协变量之集；Y表示结果；R表示一个随机化的两值处理分配，故R与U和Z相互独立，R=1表示被分配到处理组，R=0表示被分配到未处理组．YX=1表示个体接受处理的结果，对应的YX=0表示个体未接受下的结果．对于平均因果效应，将它定义为ACE=E(YX=1)-E(YX=0)．现在存在的问题在于估计总体的平均因果效应时，需要同时观测到YX=1和YX=0，但是对于每个个体，只能观测到YX=1和XX=0两者之一．显然，对于估计ACE，只能在一些假设下进行．

ACE=E(YX=1)-E(YX=0)≤

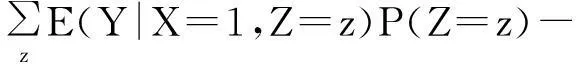
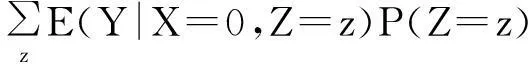
另外，可知若E(Y|X=x,Z=z,U=u)和E(X|Z=z,U=u)对于u在一个非增另一个非减的情况下可以得到ACE下界．

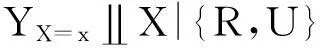
E(YX=1)=E(YX=1|R=r)≤

E(Y|X=1,R=r),

E(YX=0)=E(YX=0|R=r)≥

E(Y|X=0,R=r).

所以Chiba给出的ACE的上界如下：

ACE=E(YX=1)-E(YX=0)≤

min{E(Y|X=1,R=0),E(Y|X=1,R=1)}-

max{E(Y|X=0,R=0),E(Y|X=0,R=1)}.

另外，可知若E(Y|X=1,U=u,R=r)和P(X=1|U=u,R=r)在给定R=r时关于u一个非增另一个非减的情况下可以得到下界．

2两种不同边界的比较

以上界为例研究VanderWeele和Chiba边界的比较．

例1假设存在一个不可观测的协变量U和一个可观测的协变量Z，它们都是两值的变量且U和Z相互独立，R表示一个随机化的两值处理分配，故P(R=1)=0.5．同时令

E(Y|X=1,U=u,Z=z,R=r)=

E(Y|X=0,U=u,Z=z,R=r)=

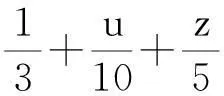
其他概率如表1所示．

其中，P000=P(X=1|U=0,R=0,Z=0)，其他记号类似，表1中最后两行的最后两列给出Vander Weele和Chiba的上界．由VanderWeele结果得到的ACE的边界为

ACE=E(YX=1)-E(YX=0)≤

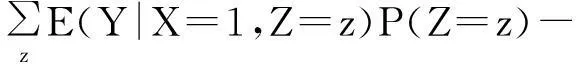
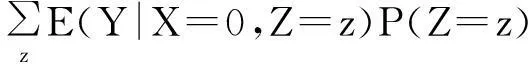
其中，

E(Y|X=1,Z=1)P(Z=1)=

P(U=u|X=1,Z=1)P(Z=1)=

(1)

其中(1)式右端第一项=E(Y|X=1,Z=1,U=1)×P(U=1|X=1,Z=1)P(Z=1)

=E(Y|X=1,Z=1,U=1)×

(2)

P(z=1,Z=1,U=1)=

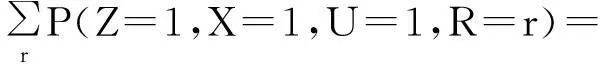
P(Z=1,X=1,U=1,R=1)+

其中，P(Z=1,X=1,U=1,R=1)=P(R=1)

P(Z=1|R=1)P(U=1|Z=1,R=1)×

P(X=1|R=1,Z=1,U=1)=

P(R=1)P(Z=1)P(U=1)×

P(X=1|R=1,Z=1,U=1).

带入给出的概率参数，即可计算出结果．类似地，可以计算出

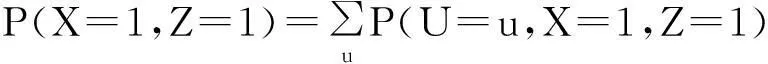
按照同样方法可以计算E(Y|X=1,Z=0)P(Z=0)，E(Y|X=0,Z=0)P(Z=0)，E(Y|X=0,Z=1)P(Z=1)，于是由VanderWeele的方法得到ACE的上界为0.1752．

由Chiba的结果给出ACE的上界如下

ACE=E(YX=1)-E(YX=0)≤

min{E(Y|X=1,R=0),E(Y|X=1,R=1)}-

max{E(Y|X=0,R=0),E(Y|X=0,R=1)}

下面举例计算E(Y|X=1,R=1).

E(Y|X=1,R=1)=

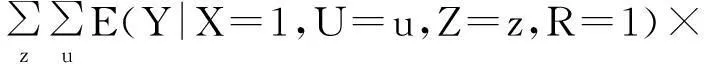
P(U=u,Z=z|X=1,R=1)=

(3)

其中(3)式右端第一项

E(Y|X=1,U=1,Z=1,R=1)×

P(U=1,Z=1|X=1,R=1)=

E(Y|X=1,U=1,Z=1,R=1)×

类似前面的计算过程，可得到由Chiba的方法给出的ACE的上界为0.1687．从中可以发现，例1中VanderWeele的上界是大于Chiba的上界的，即此时Chiba上界比VanderWeele的上界更好．

例2假设存在一个不可观测的协变量U和一个可观测的协变量Z，它们都是两值的变量并且U和Z相互独立，R表示一个随机化的处理分配，故P(R=1)=0.5．同时令

E(Y|X=1,U=u,Z=z,R=r)=

E(Y|X=0,U=u,Z=z,R=r)=

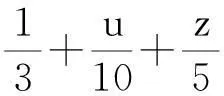
其他概率如表2所示．

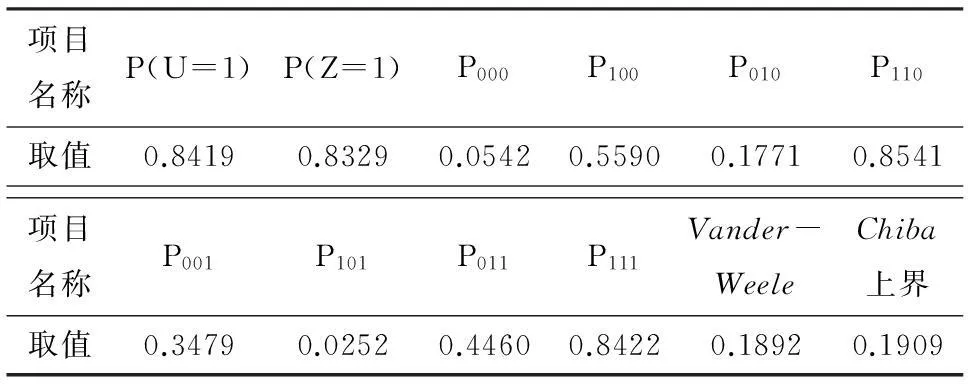
表2　例2中概率参数取值及边界计算结果

仿照例1的计算方法，可以得到由VanderWeele的方法计算的上界为0.1892，Chiba的方法计算的上界为0.1909．在这种情况时，VanderWeele的上界是小于Chiba的上界的，即此时VanderWeele的方法更好一些．

例3假设存在一个不可观测的协变量U和一个可观测的协变量Z，它们都是两值的变量并且U和Z相互独立，R表示一个随机化的处理分配，故P(R=1)=0.5．假设Y是服从高斯分布,且其均值如表3中三种不同的形式给出．在这三种不同的情况下，我们对VanderWeele和Chiba的上界进行比较．将程序运行1000次，表3中最后一行给出Chiba的上界小于VanderWeele上界的比率．本例在模拟中使用了Matlab程序和Matlab中的BNT工具箱，利用BNT工具箱计算条件概率和联合概率等[8]．

表3　Y的三种不同分布下的边界比较

从以上运行结果看，在Y服从条件高斯分布时，Vander Weele的上界小于Chiba上界的比率都在0.2左右，所以我们可以判断此时大部分情况下Chiba的改进方法确实较Vander Weele的更好，在一定程度上缩小了上界的范围，在实际情况中可以更好地应用.为了验证所给的期望值是否影响输出结果，我们在保证函数为非减的前提下对期望值做出更多改变，然后进行分析，发现得到的结果是类似的，并没有太大出入，所以可知所给的期望值并不影响输出结果的分析．

3结论

本文研究了VanderWeele和Chiba的两种不同平均因果效应边界的比较．VanderWeele的边界在单调性假设的基础上主要用到可观

测的协变量做调整，而Chiba的结果把处理分配视为一种工具变量而没有考虑到可观测协变量的作用．在例1中，Chiba方法对因果效应上界的估计要小一些，而例2中VanderWeele的方法对因果效应上届的估计要小一些，可见两种方法各有其优势，在例3中，Y服从条件高斯分布，通过模拟研究发现VanderWeele上界小的比率大约是0.2．通过进一步的模拟研究，我们发现，如果假设Y服从高斯分布，很多情况下，VanderWeele上界还是较Chiba的上界大一些．我们将在以后的研究中同时考虑可观测协变量和处理分配变量对平均因果效应边界的估计，从而进一步改进现有的结果．

参考文献：

[1]任强,谢宇.对纵贯数据统计分析的认识[J].人口研究,2011(6):3-11.

[2]Pearl J.Causal inference from indirect experiments[J].Artificial Intelligence in Medicine,1995(7):561-582.

[3]Pearl J.Causality:Models,Reasoning,and Inference[M].Cambridge:Cambridge University Press,2000.

[4]Kuroki M,Miyakawa M.Covariate selection for estimating the causal effect of control plans using causal diagrams[J].Journal of the Royal Statistical Society Series B,2003,65:209-222.

[5]耿直,何洋波,王学丽.因果链上因果效应的关系及推断[J].中国科学,2004,34:227-236.

[6]VanderWeele T J.The sign of the bias of unmeasured confounding[J].Biometrics,2008,64:702-706.

[7]Chiba Y.Bounds on causal effects in randomized trials with noncompliance under monotonicity assumptions about covariates[J].Statistics in Medinice,2009,28:3249-3259.

[8]张连文,郭海鹏.贝叶斯网引论[M].北京:科学出版社,2006.

(责任编辑:陈衍峰)