新型智能隔振复合结构的动态特性研究

第一作者王常松男，硕士生，1988年11月生

通信作者梁森男，教授，博士生导师，1962年9月生

新型智能隔振复合结构的动态特性研究

王常松1，梁森1，韦利明2

(1.青岛理工大学机械工程学院，山东青岛266033；2.中国工程物理研究院，四川绵阳621900)

摘要：针对精密机械的微位移隔振问题，设计了一种以PVDF压电薄膜为作动器和传感器的新型智能隔振复合结构。根据压电方程推导出了层叠式PVDF压电薄膜作动器厚度变形量表达式，建立了该智能复合结构的隔振理论模型，采用LMS自适应控制算法，以Matlab和有限元混合建模分析方式对本智能隔振复合结构的动态特性进行研究。有限元模型的分析结果与Matlab计算数据一致，验证了本新型智能隔振复合结构对微位移隔振的有效性，其结论将为精密仪器、微纳米设备的微位移智能主动隔振奠定理论基础。

关键词：智能结构；主动隔振；聚偏氟乙烯；最小均方自适应控制算法；有限元分析

基金项目：国家自然科学基金(51375248)和(11202198)的支助

收稿日期：2013-10-31修改稿收到日期：2014-04-16

中图分类号:TB535.1文献标志码：A

Dynamic characteristics of a new smart vibration isolation composite structure

WANGChang-song1,LIANGSen1,WEILi-ming2(1. School of Mechanical Engineering, Qingdao Technological University, Qingdao 266033, China; 2. China Academy of Engineering Physics, Mianyang 621900，China)

Abstract:In order to isolate vibration in precise instruments, a new smart composite structure was presented here, it consisted of a PVDF piezoelectric film actuator and a sensor. The deformation formula of the multilayer PVDF piezoelectric film actuator along its thickness direction was derived according to the piezoelectric equation and the vibration isolation theoretical model of this new smart composite structure was established in detail. Adopting LMS adaptive control algorithm, the dynamic characteristics of the new smart composite structure were simulated with software Matlab and ANSYS. The simulation results of ANSYS agreed well with those of Matlab, the validity of the new smart composite structure was verified. The investigation results provided an important theoretical foundation for the micro-displacement smart active vibration isolation of precise instruments and micro-nano equipments.

Key words:smart structure; active vibration isolation; PVDF; LMS adaptive control algorithm; finite element analysis

随着制造技术的发展，精密仪器和微纳米设备的应用越来越广泛，而任何微弱的振动对这些设备的正常运转都有较大的影响，这就对隔振器性能提出了很高的要求。目前，常用振动隔离的控制方法主要是被动隔振结构[1-4]，即在振动结构表面粘贴或在其内部嵌入粘弹性材料，使阻尼材料在变形中消耗更多结构振动能量达到振动控制之目的，当然调整结构刚度使系统运行远离共振区，也能提高隔振效果。这些方法的优点是减振系统的可靠性较高、稳定性好，但同时也存在不足之处，即系统一旦制作完成，很难改变其隔振特性，不能对环境变化做出适应性调节，且对精密仪器的微位移隔振效果不佳

智能结构的概念是20世纪80年代中期由美国军方提出，并在欧洲等国家经过迅速地发展，形成了一门新的交叉学科研究领域。典型的智能结构是将传感器、作动器和控制器与被控结构融合在一起而形成的一种振动主动控制系统[5]。目前国内外对智能结构的研究主要集中于板、梁结构的弯曲振动控制[6-8]，然而对压电智能结构应用于精密设备的微位移隔振的研究报道相对较少。PVDF压电薄膜作为一种新型功能高分子材料，具有压电常数高、频响范围宽、可任意裁剪等优点，是一种非常理想的传感器和主动隔振材料，在水下传感器、超声换能器等领域有广泛的研究和应用[9-10]。

为了解决仪器和微纳米设备的精密隔振问题，本文在传统智能结构的基础上提出了一种新型智能隔振复合结构，如图1所示，它是以PVDF压电薄膜为传感器和作动器，用二者之间的绝缘材料为过渡层构成一种多层复合结构，本智能隔振复合结构通过作动器在厚度方向的反相变形以补偿激励引起的振动位移，达到隔振之目的，本智能隔振复合结构在控制系统的作用下，PVDF压电薄膜针对不同的振动量和振动频率产生相应的反向变形量，解决了传统附加阻尼材料结构等被动隔振不能对环境变化做出适应性调节的问题。在理论上，通过压电方程推导PVDF压电薄膜厚度方向变形量表达式，采用LMS自适应控制算法，以Matlab和有限元混合建模分析方式对本智能隔振复合结构的动态特性进行研究，结果将为精密仪器、微纳米设备的微位移智能主动隔振奠定理论基础。

1为误差传感器，2为粘结材料层，3为绝缘材料层，4为PVDF压电薄膜作动器，5为PVDF压电薄膜初级振动传感器，6为振动结构，7为作动器电极。 图1　新型智能隔振复合结构 Fig.1 A new smart vibration isolation composite structure

1智能隔振复合结构隔振力学模型

1.1　压电效应及压电方程

在压电材料中，电效应和机械效应相互耦合，电学量和物理量之间相互影响、相互作用，压电方程正是同时包含电学量和力学量来描述这一特殊规律的物理方程。以应力和电场强度为独立变量的压电方程可描述为[11]：

(1)

式中{T}为应力分量，{S}为应变分量，{E}为电场强度，{D}为电位移强度，[CE]∈R6×6为刚度矩阵，[d]∈R3×6为压电应变常数矩阵，[εT]∈R3×3则为介电常数矩阵。

1.2　智能隔振复合结构厚度变形

本智能隔振复合结构的PVDF压电薄膜作动器极化方向为厚度方向，在平行于极化方向上给作动器施加控制电压，使其在厚度方向发生变形，因此本文仅关心PVDF压电薄膜作动器在厚度方向的参数，而压电方程为三维方程，必须简化为用厚度方向参数表示的一维方程。

将PVDF压电薄膜材料的参数矩阵[10]代入压电方程(1)，则厚度方向的应变和电位移表达式分别为：

(2)

当PVDF压电薄膜仅受厚度方向外力作用，压电薄膜四周边界应力为零，在平行于极化方向加控制电压，此时压电方程可以简化为一维形式：

(3)

设ε为PVDF压电薄膜厚度方向应变，由式(3)第一式可以得到PVDF压电薄膜厚度方向的应变表达式为：

(4)

式中，Ep、d33分别为PVDF压电薄膜材料厚度方向的弹性模量和压电应变常数，σ为PVDF压电薄膜在厚度方向所受到的应力，E则为加控制电压后PVDF压电薄膜内厚度方向上的电场强度。

设PVDF压电薄膜的厚度为tp，控制电压为U，假设电场在压电材料内部均匀分布，则压电材料内部电场强度计算可以简化为平板电容的场强计算，即

E=U/tp

(5)

设受控结构对PVDF压电薄膜作动器的压力为f，PVDF压电薄膜作动器厚度变形量为Δtp，上下侧表面面积为Ap，将式(5)代入式(4)可得PVDF压电薄膜作动器厚度变形量表达式：

Δtp=d33U-f/kp

(6)

Δtp0=d33U

(7)

PVDF压电薄膜的压电应变常数为pC/N级[12]，单层PVDF压电薄膜作动器加控制电压后的厚度变形量很小。因此，本文采用层叠式PVDF压电薄膜作动器，各层PVDF压电薄膜在电学上并联、力学上串联，作动器的总厚度变形量等于各层变形量之和。若忽略电极材料和粘结材料的影响，则n层作动器在空载和承载时的厚度变形量表达式分别为：

(8)

由式(6)~式(8)可知：当PVDF作动器空载时，其厚度变形量与压电应变常数、控制电压成正比，与PVDF压电薄膜的厚度无关，但当作动器承载时，减小PVDF压电薄膜厚度可以增大作动器的厚度变形量。因此，提高控制电压、增加作动器层数、减小PVDF压电薄膜厚度等方法可以提高作动器的厚度变形量。

对于本新型智能隔振复合结构，PVDF压电薄膜作为作动器材料，同时亦为传感器材料。当PVDF压电薄膜作为作动器时，利用的是逆压电效应；当PVDF压电薄膜作为传感器时，利用的是正压电效应，通过检测PVDF压电薄膜电极之间的电压，根据公式(7)即计算PVDF压电薄膜的厚度变形量。

1.3　智能隔振复合结构理论模型的控制分析

本智能隔振复合结构采用LMS自适应控制算法[13]，所谓的LMS算法就是系统根据环境变化自动调整权系数使其均方误差最小，根据这一原理LMS算法的最终计算表达式为：

y(n)=w(n)Tx(n)

e(n)=d(n)-y(n)

w(n+1)=w(n)+2μe(n)x(n)

(9)

式中，y(n)为LMS算法的输出信号，x(n)为输入信号，w(n)权系数，e(n)为误差信号，d(n)为参考信号，μ为步长因子。

为了验证本文理论模型所得结果的有效性，这里利用有限元软件ANSYS对结构进行动力学特性分析，在ANSYS中要同时实现压电耦合场分析和LMS自适应控制算法较为困难。因此，本文采用Matlab工具包Simulink和有限元软件ANSYS混合分析的方法，Simulink是根据理论模型式(8)进行本智能隔振复合结构的动态特性研究，有限元软件ANSYS则根据其内部的压电分析模块进行计算，但其振动激励信号和控制电压则来自Simulink理论模型分析时所用到的数据，最终再将ANSYS有限元模型分析结果与本文理论模型的Simulink计算数据进行比较，以验证本文理论模型的正确性。

本智能隔振复合结构及其LMS自适应控制算法的Simulink理论分析模型程序如图2所示，Simulink程序中分别采用正弦、白噪声、扫频等信号代表振动结构基体的激励信号，根据理论模型式(8)计算控制电压。程序中示波器模块将以图形方式显示的激励信号、控制电压、误差信号和权系数，三个“To Workspace”模块分别将激励信号、控制电压和误差信号以数据表格形式发送至Matlab前面板，其中误差信号就是本智能隔振复合结构受控后的振动信号，激励信号和控制电压在进行Simulink模型分析的同时也将作为ANSYS有限元模型分析的输入信号。移位寄存器用来更改LMS算法自适应滤波器的阶数，步长因子则通过“step size”增益模块更改。

图2　智能隔振复合结构理论模型的Simulink计算程序 Fig.2 The LMS algorithm Simulink program of the new smart vibration isolation composite structure

为了研究受控结构对本智能隔振复合结构的影响，本文分别在无负载和有负载两种情况下进行分析计算。设受控结构对作动器的作用力为20N，PVDF作动器边长为40 mm，厚度为100 μm，PVDF材料弹性模量和压电应力常数参照文献[14]，若LMS算法的步长因子取为0.002，自适应滤波器阶数取为64，计算时间取为0.2 s，则施加三种振动激励信号时Simulink计算结果如图3、4、5所示。

图3　正弦振动激励时理论模型的Simulink计算结果 Fig.3 The calculated results of theoretical model under sine excitation signal by Simulink

图4　扫频振动激励时理论模型的Simulink计算结果 Fig.4 The calculated results of theoretical model under sweep frequency excitation signal by Simulink

图5　白噪声振动激励时理论模型的Simulink计算结果 Fig.5 Thecalculated results of theoretical model under white noise excitation signal by Simulink

由图3可以看出，当激励信号为正弦激励时，受控后的振动曲线在0.04 s前迅速衰减，在0.04 s后趋于平缓逐渐达到稳定状态；由图4可以得到，当激励信号为扫频激励时，受控后的振幅在0.08 s后稳定；由图5可知，在白噪声激励条件下受控后的振幅与前两种激励相比衰减时间较长，直到0.15 s才达到稳定状态。本智能隔振复合结构对以上三种振动激励信号的隔振效果基本一致，只不过是收敛时间的长短有点差别，简单的单频信号收敛时间就短，复杂信号相应的收敛时间就稍长一点，究其原因主要在于相同步长因子条件下，对复杂度不同的信号，LMS算法获得最佳权系数w(n)所需的迭代次数不同，由式(9)LMS算法的计算表达式可知，每一次计算步所需的权系数w(n)来源于上一次计算步，当信号较为复杂时，获得最佳权系数w(n)所需的时间就会稍长一些，这样就导致白噪声振动激励信号的隔振收敛时间比正弦振动激励的隔振收敛时间长。不管收敛过程如何变化，一旦形成收敛的隔振效果，控制结果就基本保持不变。

综合图3~图5，在相同的振动激励信号条件下，本智能隔振复合结构承载时的控制电压幅值比未承载时大，但受控后的振动曲线基本相同，这说明受控结构载荷对本智能隔振复合结构的隔振效果影响甚小。

2智能隔振复合结构的有限元模型

2.1　智能隔振复合结构有限元模型建立

智能隔振复合结构在工作中，作动器和传感器之间由于厚度的变形会有耦合作用力，但这样的作用力很弱，为了便于有限元分析，本文在有限元求解时忽略作动器和传感器之间耦合作用。

根据该智能隔振复合结构的特点，采用SOLID5单元定义PVDF压电材料，SOLID5是三维耦合场八节点六面体单元[15]，而振动结构则采用八节点三维实体单元SOLID45。PVDF材料密度为1.78×103kg/m3[11]，PVDF材料弹性模量和压电应力常数同1.3节Simulink理论模型。振动结构采用钢，其材料参数弹性模量E=2.1 GPa，密度ρ=7.8×103kg/m3，泊松比μ=0.3[16]。

本智能隔振复合结构的PVDF作动器压电材料的极化方向为厚度方向，作动器在厚度方向发生变形，因此在ANSYS中将z轴定义为厚度方向， PVDF压电薄膜尺寸参数同1.3节Simulink理论模型，而振动结构厚度为1 mm，单层PVDF作动器和振动结构的有限元模型如图6(a)所示。

由于PVDF压电薄膜材料层和振动结构相互耦合，划分网格前，PVDF压电薄膜与振动结构之间使用GLUE命令进行粘结处理。划分网格时，考虑到有限元计算精度和计算量的问题，在对计算结果影响较大的厚度方向网格划分比较密集，而在长度和宽度方向，网格划分可以相对稀疏，划分网格如图6(b)所示。

图6　智能隔振复合结构的有限元模型及网格划分 Fig.6 The finite element model and mesh of the new smart vibration isolation composite structure

2.2　智能隔振复合结构作动器动态特性有限元分析

为了研究智能隔振复合结构的动态响应，下面分别在无负载和有负载条件下进行有限元动态特性分析，这里所谓的无负载和有负载指是否考虑被控结构对本智能隔振复合结构的压力。为了简化计算，有限元模型分析时的振动激励信号和相应的控制电压来源于Simulink理论模型计算时所用到的数据。

有限元ANSYS模型有负载时，将该负载简化为被控结构对本智能隔振复合结构的压力，同1.3节Simulink理论模型计算均为20N，该压力将直接施加在有限元模型中，而振动激励信号和控制电压数据则以表格形式导入有限元软件ANSYS中，在ANSYS瞬态动力学分析模块中求解，使用POST26时间历程后处理器分别提取不同激励下受控后本智能隔振复合结构的振动数据，并做出其振动曲线，如图7所示。

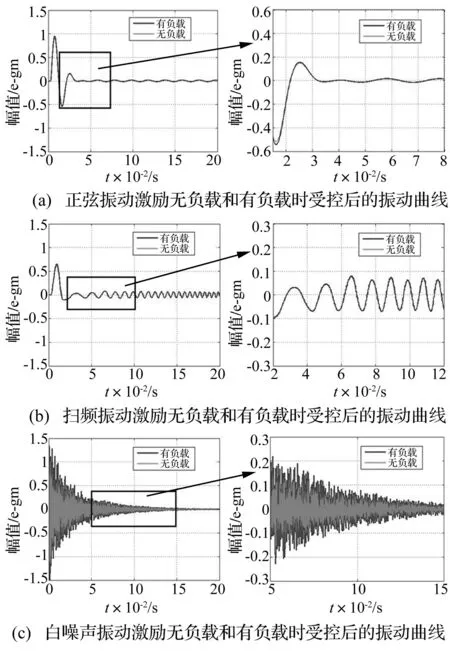
图7　不同振动激励条件时有限元模型ANSYS分析结果 Fig.7 The calculated results of finite element model under different excitation signal by ANSYS

由图7(a)可以看出，当激励信号为正弦激励时，AYSYS有限元模型受控后的振动曲线在0.04 s后趋于平缓逐渐达到稳定状态；由图7(b)可以得到，当激励信号为扫频激励时，AYSYS有限元模型受控后的振幅在0.08 s后稳定；由图7(c)可知，AYSYS有限元模型在白噪声激励条件下受控后的振幅与前两种激励相比衰减时间较长，直到0.15 s才达到稳定状态。将图7(a)、(b)、(c)分别与图3、4、5理论模型受控后的振动曲线比较，有限元模型分析结果与本文理论模型的Simulink计算数据结果在有负载和无负载时均能较好吻合，验证了本文推导出理论模型公式的正确性和本智能隔振复合结构能对精密设备的微位移进行有效隔振。

3结论

由于PVDF压电薄膜材料的厚度方向压电应力常数为pC/N级，因此由该材料制成的压电作动器厚度变形量为微米级，正是这样的特点使本智能隔振复合结构非常适用于精密和微纳米仪器的微位移隔振。本文针对精密设备的微位移隔振问题设计了一种以PVDF压电薄膜为作动器和传感器的新型智能隔振复合结构，以压电方程为基础建立了新型智能隔振复合结构的系统模型，该模型表明厚度变形量与压电应变常数、控制电压、作动器层数等因素有关。采用LMS自适应控制算法，以Matlab和有限元软件ANSYS混合建模分析方式对本智能隔振复合结构的动态特性进行研究，有限元软件ANSYS的模型分析结果与Matlab计算数据一致，这表明本智能隔振复合结构可以有效的控制正弦、扫频、白噪声等一系列不同激励条件引起的振动。研究结论将为航空航天设备、微纳米精密仪器的微位移智能主动隔振奠定理论基础。

参考文献

[1]Granger D, Ross A. Effects of partial constrained viscoelastic layer damping parameters on the initial transient response of impacted cantilever beams: Experimental and numerical results [J].Journal of Sound and Vibration, 2009, 321(1): 45-64.

[2]梁森，梁磊，米鹏．嵌入式共固化复合材料阻尼结构的新进展[J]．应用力学学报，2010,27(4)：767-772．

LIANG Sen, LIANG Lei, MI Peng.New development of the embedded and co-cured composite damping structures [J]. Chinese Journal of Applied Mechanics, 2010, 27 (4) 767-772.

[3]Lee J T. Active structural acoustics control of beams using active constrained layer damping through loss factor maximization[J]. Journal of Sound and Vibration, 2005, 287(14):481-503.

[4]李强,徐登峰,范新,等.新型永磁隔振器的隔振性能分析与实验研究[J].振动与冲击,2013,32(13):6-12.

LI Qiang, XU Deng-feng, FAN Xin, et al.Analysis and test of vibration isolation performance for a novel permanentmagnet vibration isolator[J].Journal of Vibration and Shock,2013,32(13):6-12.

[5]钱锋.层合压电智能结构振动主动控制数值模拟及其优化[D] .合肥：合肥工业大学, 2011.

[6]Hadjigeorgiou E P, Stavroulakis G E, Massalas C V. Shape control and damage identification of beams using piezoelectric actuation and genetic optimization [J]. International Journal of Engineering Science, 2006, 44: 409-421.

[7]Ducarne J, Thomas O, Deu J F. Shape control and damage identification of beams using piezoelectric actuation and genetic optimization [J]. Journal of Sound and Vibration, 2012, 331: 3286-3303.

[8]钱锋,王建国,汪权,等.基于模态应变能分布的压电致动器/传感器位置优化遗传算法[J].振动与冲击, 2013,32(11):161-166.

QIAN Feng，WANG Jian-Guo，WANG Quan，et al. Optimal placement of piezoelectric actuator /sensor using genetic algorithm based on modal strain energy distribution[J]. Journal of Vibration and Shock, 2013,32(11):161-166.

[9]Shirinov A V, Schomburg W K. Pressure sensor from a PVDF film [J]. Sensors and Actuators A: Physical, 2008, 142(1):48-55.

[10]Rathoda V T, Mahapatraa D R, Anjana Jainb, A. Gayathrib. Characterization of a large-area PVDF thin film for electro-mechanical and ultrasonic sensing applications [J].Sensors and Actuators A: Physical, 2010, 163(1):164-171.

[11]张福学，王丽坤．现代压电学上册[M]．北京：科学出版社，2001．

[12]Mark J E. Polymer data handbook [M].New York: Oxford University Press, Inc, 1999:949-955.

[13]Tang X L, Lee C M. Time-frequency-domain filtered-x LMS algorithm for active noise control [J]. Journal of Sound and Vibration, 2012, 331(23): 5002-5011.

[14]Vel S S, Batra R C. Three dimensional analytical solution for hybrid multilayered piezoelectric plates [J]. Journal of Applied Mechanics, 2000, 67: 558-567.

[15]Ansys, Inc. Ansys Coupled-Field Analysis Guide Release 14.0[M]. Southpointe: ANSYS, Inc, 2011.

[16]曾正明．机械工程材料手册第六版[M]．北京：机械工业出版社，2003．