基于频率截止的EEMD方法研究

第一作者黄杰男，硕士生，1989年10月生

基于频率截止的EEMD方法研究

黄杰,张梅军,柴凯,陈灏

(解放军理工大学野战工程学院，南京210007)

摘要：为解决总体平均经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)中虚假IMF分量过多问题，提出了一种基于频率截止的EEMD方法。该方法采用一种新的IMF筛分终止条件——以信号自身的最小频率为EMD分解IMF分量的截止频率；然后将基于频率截止的IMF筛分终止条件引入EEMD分解。通过仿真和实测信号分析，并与EMD、EEMD分解结果比较得到，运用频率截止的EEMD方法不仅有效减少了虚假IMF分量的产生，使得分解的目的性更加明确，而且保证了EEMD分解出的IMF分量的完备性，更好地抑制了模态混叠现象。

关键词：总体平均经验模态分解；频率截止；模态混叠；IMF分量

基金项目：2011年度国家自然科学

收稿日期：2014-01-27修改稿收到日期：2014-04-10

中图分类号:TH137文献标志码：A

An improved EEMD method based on cut-off frequency

HUANGJie,ZHANGMei-jun,CHAIKai,CHENHao(College of Field Engineering, PLA Univ. of Sci. & Tech.，Nanjing 210007, China)

Abstract:In order to solve the problem of excessive false IMF components in ensemble empirical mode decomposition(EEMD), an improved EEMD method based on cut-off frequency was proposed here. This method adopted a new screening termination condition of IMF, the minimum frequency of a signal itself was taken as the cut-off frequency when using EMD. Then, the screening termination condition of IMF based on cut-off frequency was introduced into the EEMD. Comparing the results of EMD and EEMD with those of the improved EEMD, it was shown that the false IMF components are reduced more effectively and the mode mixing phenomenon is suppressed with the improved EEMD method based on cut-off frequency in analyses of simulated and actually measured signals; the IMF components are complete and the purposiveness of decomposition is more clear with this proposed method.

Key words:ensemble empirical mode decomposition (EEMD); cut-off frequency; mode mixing; IMF components

经验模态分解(Empirical Mode Decomposition, EMD)基于信号本身的局部特征时间尺度，自适应地将信号分解为有限多个固有模态函数(Intrinsic Mode Function, IMF)之和，被广泛应用于非线性非平稳信号的处理。但是，EMD方法存在许多值得研究的问题，如模态混叠、IMF筛分终止条件以及端点效应等问题[1]。

为减少EMD的模态混叠缺陷，Wu等[2]提出了利用噪声辅助分解的总体平均经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)，取得了较好效果。但是，该方法存在两个问题：①由于信号加入白噪声后，每次分解的IMF个数可能不一致而影响最终IMF的平均，因此为简化分解，该方法在单次的IMF分解循环中只作了10次包络均值相减，便将结果作为一个IMF分量，没有严格执行IMF的两个判据条件；②其IMF分量个数由信号长度决定，而非分解过程所决定，因此，对于一个频率成分少而信号长度大的信号，依然会产生多阶冗余虚假IMF分量。

EMD分解中，IMF筛分终止条件决定了IMF分量的个数以及是否具有真实物理意义，关于EMD的IMF筛分终止条件[3]，以往的研究主要有SD阈值终止条件[4]、基于零点和极值点的终止条件[5]， 基于幅值比的终止条件[6]，基于能量差跟踪法的终止条件[1]，基于能量的终止条件[7]等。除基于能量的终止条件外，其他方法分解的IMF分量多，且存在多个与信号无关的虚假低频分量，不具实际意义。

因此，本文提出一种基于频率截止的EEMD方法。该法以信号本身的最小频率为截止频率fd，作为EEMD分解IMF分量的终止条件。并且以完整的EMD分解过程替换了Wu等所提EEMD方法中简化的EMD分解过程，保证了IMF分量分解的完备性。通过对仿真信号和实测信号的分析，运用频率截止的EEMD方法得出的虚假IMF分量少、分解速度快、分解目的性强、且模态混叠现象得到了更好的抑制。

1基于频率截止的EEMD方法

EEMD方法利用高斯白噪声具有频率均匀分布的统计特性来解决模态混叠问题[8]。由于白噪声具有在各个频段能量一致和均值为零的特性，通过在原始信号中引入白噪声后再进行EMD分解可以保证分解得到的每阶IMF分量在时域上的连续性。在原始信号中循环引入足够多组不同的白噪声后，经EMD分解可以得到多组IMF分量；为消除白噪声的影响，对应的各组IMF分量分别求取平均值后作为最终分解结果。本文提出的基于频率截止的EEMD方法是在Wu与Huang的EEMD基础上改进的，但EMD分解过程不再简化分解，而是嵌入了完整的EMD分解。具体实现步骤如下：

(1)对原信号s(t)进行功率谱分析，找出明显频率成分中最小的频率作为分解的截止频率，记为fd。

(2)给信号s(t)加入给定幅值的白噪声ni(t)(白噪声的标准差取原信号标准差的0.01~0.1倍)，即：

si(t)=s(t)+ni(t)

(1)

(3)对si(t)进行EMD分解(本文中EMD分解采用的是Rilling提出的方法)。每分解出一个IMF分量cj,i，对cj,i作功率谱分析，找出其主要频率成分fmax，比较fmax和fd的大小，若fmax小于fd，分解停止，否则分解继续。得到一组IMF分量c1,i，c2,i，…，cn,i。

(4)重复步骤(2)、(3)M次，得到M组IMF分量。

(5)计算M次分解的IMF的总体平均ck，这n个IMF分量即为EEMD分解最终的IMF分量：

k=1,2…n

(2)

2仿真信号分析

为验证基于频率截止的EEMD方法的改进效果，对图1所示的仿真信号(式(3))，分别进行EMD分解、经典EEMD分解和基于频率截止的EEMD分解，比较分解结果。仿真信号主要有30 Hz和100 Hz两个频率成分。研究中，EMD分解采用Rilling编写的EMD方法、经典EEMD分解采用Wu与Huang提出的EEMD方法。总体平均次数M取50，噪声标准差为信号标准差的0.02倍，由于该仿真信号最小频率为30 Hz，所以频率截止的EEMD方法取截止频率fd=30 Hz。

(3)

图1　仿真信号 Fig.1 Simulation signal

2.1　仿真信号的EMD分解

仿真信号由EMD分解得到了6阶IMF分量和1阶余量(图2)，将图2和原信号图1比较可知：仿真信号的EMD分解结果与原信号有较大的差别，分解的结果不太理想。对分解的IMF分量做功率谱分析如图3。

图2　仿真信号的EMD分解结果 Fig.2 The EMD result of simulation signal

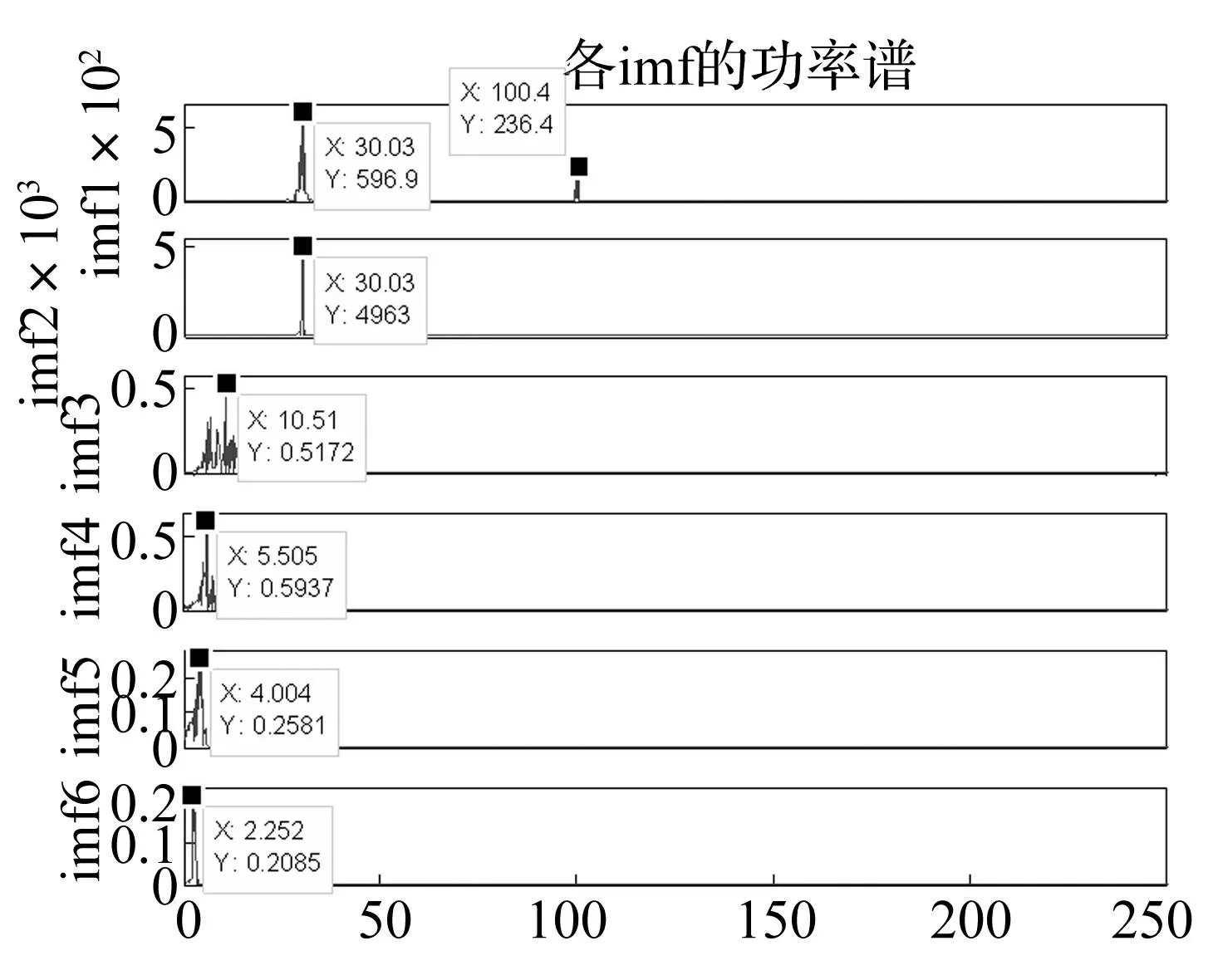
图3　EMD分解出的IMF的功率谱 Fig.3 The power spectrum of IMFs by EMD

从IMF分量的功率谱(图3)可以看出：仅IMF1和IMF2包含了信号中的真实成分，后4阶IMF分量都是分解过程中产生的虚假成分，没有实际意义；且IMF1分量中存在30 Hz和100 Hz两个不同频率的成分，IMF2中也有30 Hz的频率成分，发生了频率混叠。

2.2　仿真信号的经典EEMD分解

仿真信号由经典EEMD分解得到了10阶IMF分量和1阶余量(图4)，前2阶IMF分量与原信号(图5)相比较为一致。由于分量过多，仅对前五阶IMF分量进行功率谱分析，如图5。

图4　仿真信号的经典EEMD分解结果 Fig.4 The EEMD result of simulation signal

图5　经典EEMD分解出的部分IMF的功率谱 Fig.5 The power spectrum of part of IMFs by EEMD

由图可见采用经典的EEMD方法时，100 Hz的调幅成分分解到了IMF1中，但30 Hz的正弦波成分却被分解到了IMF2和IMF3之中，模态混叠现象得到了一定的抑制。分解出的IMF仅前3阶IMF分量包含了信号的真实成分，其余的7阶IMF分量都是冗余的虚假成分。

2.3　仿真信号采用基于频率截止的EEMD分解

仿真信号采用本文提出的频率截止EEMD分解结果如图6，分解得到了2阶IMF分量和1阶余量。对得到的IMF分量进行功率谱分析如图7。

图6　仿真信号采用频率截止的EEMD分解结果 Fig.6 The decomposition result of simulation signal by EEMD based on cut-off frequency

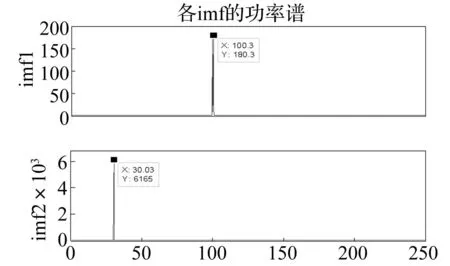
图7　采用频率截止的EEMD分解出的IMF的功率谱 Fig .7 The power spectrum of IMFs by EEMD based on cut-offfrequency

由图6和图7可以看出，采用基于频率截止的EEMD方法分解信号时，信号中的两个频率成分都能完好的分解出来，没有多余的IMF分量，分解效率高，而且没有出现模态混叠。究其原因在于：

EMD的分解过程类似于一个自适应的二进滤波，由于信号的时间尺度并不连续，所以会产生模态混叠现象[9]。EEMD方法中加入的白噪声平均分布在整个时间和频率尺度上，因此EEMD方法能有效抑制模态混叠，但是经典EEMD方法中的EMD分解过程是简化了的过程，只做了10次包络均值相减的循环，分解不完备，仍然存在模态混叠。本文提出的频率截止的EEMD方法中采用了完整的EMD分解过程，分解出的IMF分量都满足IMF的两个判据条件，因而取得了更好的效果。

EMD分解时，筛分会一直进行，直到残余函数为一个单调函数，因而其IMF分量个数由分解过程决定。经典EEMD分解的IMF分量个数由数据长度决定，仿真信号数据长度为4000，根据分解程序中的IMF分量个数公式N=fix(log2(xsize))-1可知，不论仿真信号频率成分有多少，其IMF个数都为10，显然这并不合理。本文提出的频率截止的EEMD方法在分解时只要达到截止频率的要求，分解便会终止，因此几乎没有冗余虚假分量，实际应用时将会大大提高效率，而且分解的目的性非常明确。

3实测信号分析

选择的实测信号为液压故障平台上测得的某故障信号(图8)，采样频率为5 000 Hz，采样点数为2 048，实测信号的功率谱如图9，最小频率为29.32 Hz，因此分解截止频率取为29.32 Hz。

图8　实测信号 Fig.8 The measured signal

图9　实测信号功率谱图 Fig. 9 The power spectrum of measured signal

3.1　实测信号采用基于频率截止的EEMD分解

实测信号采用频率截止的EEMD分解结果如图10，其IMF分量的功率谱如图11。

图10　实测信号采用频率截止的EEMD分解结果 Fig.10 The decomposition result of measured signal by EEMD based on cut-off frequency

图11　实测信号采用频率截止的EEMD分解的IMF的功率谱 Fig.11 The power spectrum of IMFs of measured signal by EEMD based on cut-off frequency

图12　实测信号经典EEMD分解图 Fig.12 The EEMD result of measured signal

图13　实测信号经典EEMD分解的前7阶IMF的功率谱 Fig.13 The power spectrum of top seven IMFs of measuredsignal by EEMD

将图11与原信号的功率谱图(图9)作比较可知，原信号中各主要频率成分都被分解出来了，不同的频率分量分解在不同的IMF分量中，没有产生频率混叠。

3.2　实测信号采用频率截止的EEMD分解的对比验证

为验证频率截止的EEMD方法分解的效果，对实测信号进行经典的EEMD分解(图12)，图13是实测信号经典EEMD分解的前7阶IMF分量的功率谱图。

经典EEMD分解的IMF分量中，IMF3和IMF4都包含了239.5 Hz的频率成分、IMF5和IMF6都包含了29.33 Hz的频率成分，模态混叠现象比较明显。相比之下，采用频率截止的EEMD的分解结果(图11)不同的频率成分分解在不同的IMF分量中，基本没有产生模态混叠。表1是两种EEMD方法的分解对比。

表1　两种EEMD分解对比

由表1可见：实测信号采用频率截止的EEMD分解出的IMF分量数量仅为经典EEMD分量的一半，而经典EEMD分解多出的5阶IMF分量俱为虚假低频分量。采用频率截止的EEMD中嵌入完整的EMD分解过程，会使单次分解会耗时增加，但当截止频率较大时，由于分解的IMF分量的数量大幅减少，因此，本文实测信号分解时总体耗时反而更少，更具有优势。

4结论

针对EEMD分解中会产生大量的虚假IMF分量问题，本文提出了一种基于频率截止的EEMD方法。

(1)提出了一种新的IMF筛分终止条件，该方法以信号自身的最小频率作为分解的截止频率，有效减少了虚假IMF分量，使得分解目的性更明确。

(2)在经典EEMD方法的基础上，将兼有频率截止的完整的EMD分解过程引入EEMD分解，保证了EEMD分解过程的完备性，通过对仿真信号和实测信号验证，运用频率截止的EEMD方法能更好地抑制模态混叠现象。

(3)应用本文方法分解信号时，选择的截止频率为信号自身明显频率成分中最小的频率。若这个最小频率较大，那么分解的IMF数量少，耗时短，频率混叠基本消失，分解效果好。若最小频率小，优越性则难以体现。

参考文献

[1]程军圣，于德介，杨宇．经典模态分解方法中内禀模态函数判据问题研究[J]．中国机械工程，2004，15(20)：1861-1864．

CHENG Jun-sheng，YU De-jie，YANG Yu．Research on the criterion problem of intrinsic mode function by empirical mode decomposition[J]．China Mechanical Engineering，2004，15(20)：1861-1864．

[2]Wu Z H，Huang N E．Ensemble empirical mode decompositio：A noise-assisted data analysis method[J].Advances in Adaptive Data Analysis，2008，1(1): 1-41．

[3]胥保春，袁慎芳．IMF筛选停止条件的分析及新的停止条件[J]．振动、测试与诊断，2011， 31(3)： 348-352．

XU Bao-chun，YUAN Shen-fang，The analysis of IMF’s screening stop condition and a new stop condition[J] ．Journal of Vibration，Measurement & Diagnosis，2011， 31(3)： 348-352．

[4]Huang N E，Zhen S，Long S R，et a．The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proceedings of the Royal Society of London，1998，454：903-995.

[5]Huang N E，Zhen S，Long S R．A new view of nonlinear water waves：the Hilbert spectrum[J]. Annual Review of Fluid Mechanics，1999，31：417-457．

[6]Rilling G，Flandrin P．On empirical mode decomposition and its algorithms[C]// IEEE-EUBASIP Workshop on Nonlinear Signal and Image Processing(NSIP2003)， Grado, Italy：[s.n.]， 2003．

[7]胡劲松，杨世锡．基于能量的振动信号经验模态分解终止条件[J]．振动、测试与诊断，2009，29(1):19-22．

HU Jing-song，YANG Shi-xi ．The termination condition of empirical mode decomposition based on energy of vibration signal[J] ．Journal of Vibration，Measurement & Diagnosis，2009，29(1):19-22．

[8]雷亚国．基于改进Hilbert-Huang变换的机械故障诊断[J]．机械工程学报, 2011，47(5)： 71-77．

LEI Ya-guo．Machinery fault diagnosis based on improved Hilbert-Huang transform [J]．Chinese Journal of Mechanical Engineering，2011，47(5)：71-77．

[9]齐天，裘焱，吴亚锋．利用聚合经验模态分解抑制振信号中的模态混叠[J]．噪声振动与控制，2010(4)：103-106．

QI Tian，QIU Yan，WU Ya-feng．The suppression of mode mixing in the ensemble empirical mode decomposition of vibration signal[J] Noise and Vibration Control，2010(4)：103-106．