斜拉索风雨振气动抑振措施的参数优化

第一作者刘庆宽男，博士，教授，1971年1月生

斜拉索风雨振气动抑振措施的参数优化

刘庆宽,郑云飞,白雨润,邵奇,刘小兵,马文勇

(石家庄铁道大学，石家庄050043)

摘要：通过风洞试验，研究了斜拉索空间位置、降雨量、风速等对斜拉索风雨振的影响，选定了振动最大时的参数，研究了作为气动抑振措施的螺旋线直径和缠绕间距两个参数对抑振效果的影响，并研究了附加不同参数螺旋线时斜拉索的气动阻力系数随雷诺数的变化规律，发现针对该研究选定的直径155 mm的斜拉索，斜拉索的水平角35°、竖向角25°、较小的降雨强度(10 mm/h)、特定的风速范围(无量纲风速60~100)下发生的振动最为激烈；在选定螺旋线间距的情况下，随着螺旋线直径的增大，其抑振效果趋于显著；在选定螺旋线直径的情况下，随着螺旋线间距的减小，其抑振效果趋于显著；附加螺旋线斜拉索的气动阻力系数随螺旋线直径的增大或螺旋线缠绕间距的减小而增大。在超临界雷诺数区域，附加螺旋线时的阻力系数均大于无螺旋线时的阻力系数。提出了优化的螺旋线设计原则。

关键词：斜拉索；风雨振；气动措施；螺旋线；气动力

基金项目：国家自然科学

收稿日期：2013-10-24修改稿收到日期：2014-04-25

中图分类号:U441.3文献标志码：A

Parametric optimization of aerodynamic anti-vibration measure for rain-wind induced vibration of cables

LIUQing-kuan,ZHENGYun-fei,BAIYu-run,SHAOQi,LIUXiao-bing,MAWen-yong(Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

Abstract:With wind tunnel tests, the effects of cable altitude, rainfall intensity, and wind velocity on rain-wind induced vibration of cables of a cable-stayed bridge were studied. The cable model was built when it got the largest vibration amplitude. The effects of two parameters including helical line diameter and twine space on rain-wind induced vibration of cables were studied, and the aerodynamic drag force coefficients of cable with different helical lines were measured under different Reynolds numbers. Results showed that for the cable model with diameter of 155mm, with the parameters of horizontal angle 35°, vertical angle 25°, smaller rainfall intensity (10mm/h) and certain wind velocity (non-dimensional wind velocity 60~100), the cable vibration reaches the largest amplitude; with a certain twine space of helical line, the anti-vibration effect increases with increase in the diameter of helical line; with a certain diameter of helical line, the anti-vibration effect increases with decrease in twine space of helical line; the aerodynamic drag force coefficient of cable with helical line increases with increase in helical line diameter or decrease in helical line twine space. Finally, the optimization design rule of helical line was proposed.

Key words:stay-cable; rain-wind induced vibration; aerodynamic anti-vibration measure; helical line; aerodynamic force

斜拉索在风雨环境下大幅振动的问题(斜拉索风雨振)，因为发生频繁、危害严重，引起了设计和科研人员的重视，并成为桥梁抗风研究的一大热点和难点问题[1-3]。围绕其振动机理和抑振措施，相关的研究者通过现场观测、风洞试验、理论分析和数值流体计算(CFD)等各种方法进行了研究，提出的与水线有关的振动机理有水线驰振理论[4-5]、高风速涡致振动理论[6]、水线摆动理论[7-10]、卡门涡抑制理论[11]等。除水线之外，还有轴向流理论[11]、雷诺数影响理论等[12-13]。为了防止振动的发生，目前的方法有机械措施、结构措施和气动措施。

从机理分析可知，斜拉索表面水线的形成对振动的产生具有十分重要的作用。据此，以防止水线的形成为目标的措施，如设置纵向肋条、表面设置凹坑、表面缠绕螺旋线等，成为目前最常用、也被认为是最有效的方法。采用螺旋线措施时，为了达到效果，斜拉索的直径、螺旋线的直径和间距、缠绕方式等参数(如图1所示)的选取是十分重要的。除去需要考虑抑振效果之外，抑振措施对风荷载的影响也是不容忽视的问题，尤其是对于大跨径斜拉桥，斜拉索上的风荷载会占到全桥风荷载的很大比例。以苏通长江公路大桥为例，在横桥向风的作用下，斜拉索上的风荷载对于主梁位移和内力的贡献占总体的60%～70%[14]。

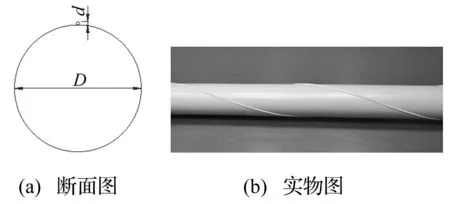
图1　斜拉索风雨振气动措施：螺旋线 Fig.1 Aerodynamic countermeasures against Rain-wind induced vibration: helical line

因此，在保证抑振效果的前提下，尽量减小带螺旋线的斜拉索的气动力，是有意义的研究课题。

本文通过风洞试验，首先再现了斜拉索风雨振现象，通过改变相关参数，找到了振幅最大时的斜拉索空间角度、降雨强度和风速等参数；其次，改变螺旋线的直径、间距等参数，检验了各个参数对抑振效果的影响；最后，测试了附带各种参数螺旋线的斜拉索的气动力，指出了螺旋线参数的设计原则。

1风洞试验介绍

本研究使用的风洞是石家庄铁道大学的回/直流可变双试验段大气边界层风洞(如图2所示[15])。其低速试验段宽4.4 m，高3.0 m，长24.0 m，最大风速≥30.0 m/s；高速试验段宽2.2 m，高2.0 m，长5.0 m，最大风速≥80.0 m/s。其中第一、第二拐角可以推开，变回流为直流结构，可以进行风雨联合等不适合在回流风洞中进行的试验。

图2　风洞平面图 Fig.2 Wind tunnel plane

图3　风雨振试验系统 Fig.3 System of Rain-wind induced vibration

本研究共进行了两类试验，第一类是测试风雨振的振幅与相关参数关系、螺旋线抑振效果的试验，在风洞直流状态下的第一拐角区进行(图2中灰色部分)。拐角位置试验模型区风场不均匀性δV≤1.5%，满足风雨振试验的要求。降雨模拟采用专门定制的降雨模拟系统完成，该系统由控制系统(可实现开环或闭环控制)、供水系统、喷淋系统组成，其中喷淋系统由处于不同空间位置的4组12个不同口径的喷头组成，通过控制系统调整压力，可以准确模拟从10 mm/h到240 mm/h的各级降雨强度的降雨，同时在雨滴谱等特性方面与自然降雨保持一致。降雨强度的精度为2%，降雨范围为宽4 m，顺风向长度4 m。斜拉索模型通过弹簧悬挂安装在专门的支架上，可以通过支架底座的机构转动整个圆环，来调整斜拉索的水平角β，通过转动圆环的内环(外环不可转动，固定在底座上)，来调整斜拉索的竖向角α。试验系统见图3所示。

整个试验系统中，风速由风洞控制系统调节，在风洞第一扩散段尾部的洞体底板上安装了澳大利亚Turbulent Flow Instrumentation 公司生产的4孔眼镜蛇探头(4-hole Cobra Probe)，于正式试验前标定了探头位置与模型中心位置之间的风速对应关系，试验中模型处的风速由探头记录的风速算得。斜拉索模型的振幅时程由安装在模型悬挂装置上的位移传感器测试。

试验模型长2.5 m，直径D=155 mm，频率f=1.03Hz， 阻尼比ξ=0.11%。由于水线的形成需要斜拉索模型具有足够的长度，且需要水量的积累，模型的两个端部，尤其上端部会影响水线，离上端部一定距离内的模型上无法形成水线，因此对于实际斜拉索有可能振动的情况下，模型试验可能不发生振动，造成结果偏于危险。为了弥补该问题，本试验系统的Sc(Sc=4 πmξ/ρD2)数设置值比实际数要小。本研究的Sc约为10,对应直径实际斜拉索的Sc在40左右。

本研究的第二类试验是斜拉索模型气动力测试试验，在风洞的高速试验段进行，流场为低湍流度的均匀流场。模型长度1.7 m，直径D=155 mm，气动力由端部安装的美国ATI公司生产DELTA系列六分力高频天平测试。模型气动阻力和气动升力方向上量程330 N，满量程精度1/16N，固有频率1 500 Hz，计算刚度为3.6×107N/m。试验照片如图4所示。

图4　测力试验照片 Fig.4 Aerodynamic force measurement

2斜拉索风雨振振幅的影响因素

相关学者针对斜拉索的参数与振动振幅间的关系进行了相对较为深入的研究，但是不同的试验系统和不同模型等参数下，试验结果可能有一定的差别。为了确定在本试验系统下斜拉索发生最大振幅时的空间位置、降雨强度、风速等参数，首先研究了上述三套参数与斜拉索振幅的关系，以便选定发生最大振幅时的参数，在此基础上进行抑振效果的试验研究。

根据以前经验和研究结果，设定斜拉索的角度分别为α=25°，β=35°的情况下，改变风速和降雨强度，得到斜拉索振动振幅，如图5所示。可以看出，在相对较小的降雨强度(10 mm/h前后)和特定的风速范围(15 m/s前后)，斜拉索发生振动的振幅较大。

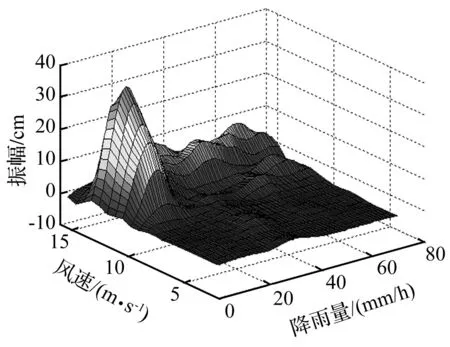
图5　振幅与风速和雨强的关系(α=25°，β=35°) Fig.5 Relation between vibration amplitude and rainfall intensity, wind velocity (α=25°，β=35°)

图6　竖向角α与振幅的关系(降雨强度10 mm/h) Fig.6 Relation between α and amplitude (rainfall intensity 10 mm/h)

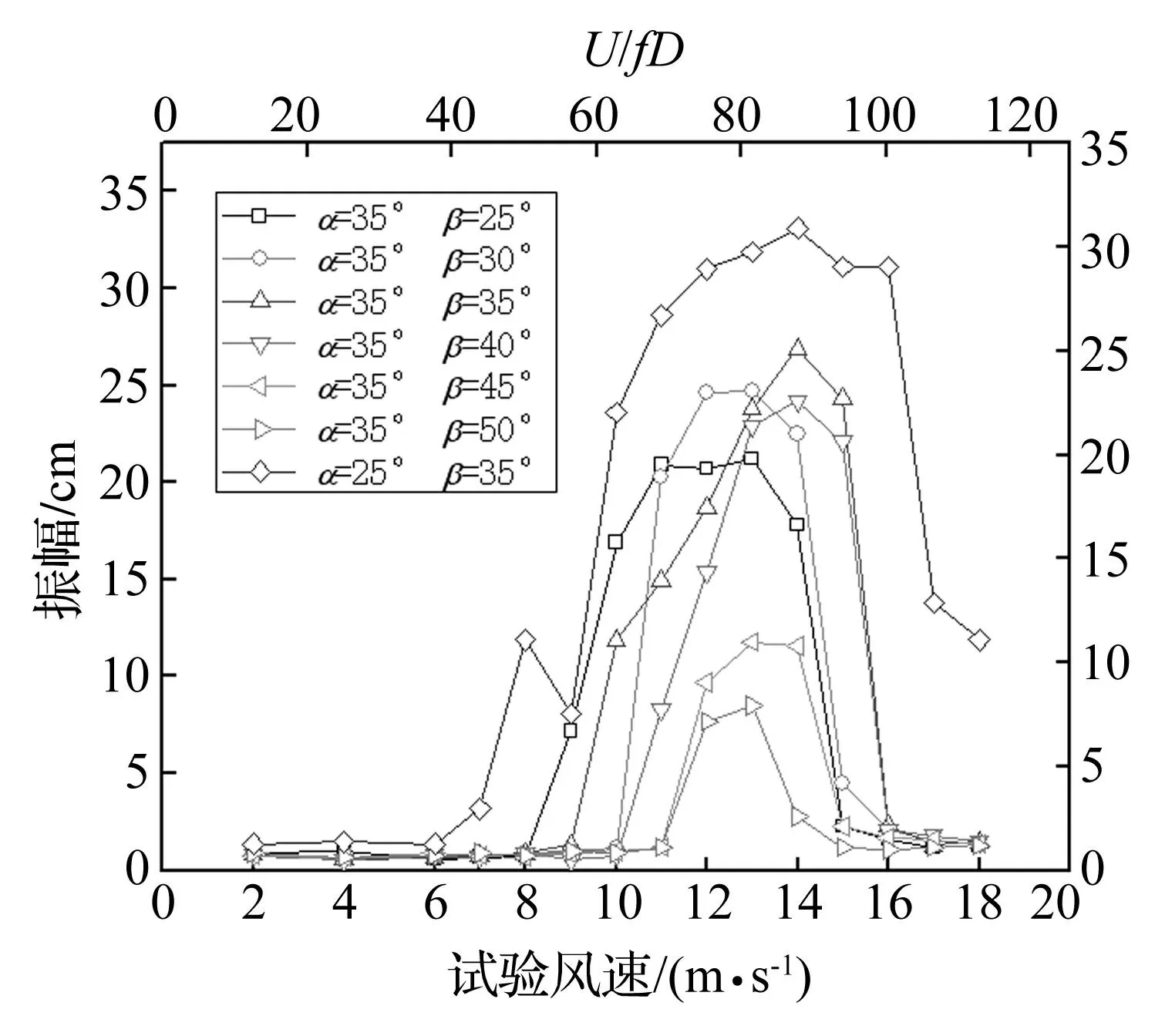
图7　水平角β与振幅的关系(降雨强度10 mm/h) Fig.7 Relation between β and amplitude (rainfall intensity 10 mm/h)

以10 mm/h的降雨强度为基础，固定水平角β，改变竖向角α，各风速下振幅如图6所示。这里为了比较，列上了α=25°，β=35°的结果。

同样，以10 mm/h的降雨强度为基础，固定竖向角α，改变水平角β，各风速下振幅如图7所示，同样列上了α=25°，β=35°的结果。

3螺旋线参数对抑振效果的影响

通过上节的分析可知，在降雨强度10 mm/h、竖向角α=25°、水平角β=35°、风速10~16 m/s(无量纲风速60~100)的情况下，斜拉索发生较大振幅的振动。固定这些参数，在斜拉索表面缠绕不同参数的螺旋线，来考察螺旋线的抑振效果。

采用双螺旋线，缠绕方向为顺时针方向(缠绕方向定义：从模型较高一端向较低一端看，螺旋线从模型较低一端向上缠绕，缠绕的方向为顺时针时，定义为顺时针方向，反之定义为逆时针方向)。螺旋线的间距S分别为6D、8D、10D、12D，其中D为斜拉索模型的直径，螺旋线的直径分别为0.7 mm、1.2 mm、1.6 mm、2.0 mm和3.0 mm。振动系统的频率为1.03 Hz，阻尼比为0.11%，试验风速范围为2~18 mm/s。

固定螺旋线的S间距为12D，改变螺旋线的直径，得到不同螺旋线直径下的振幅如图8所示。

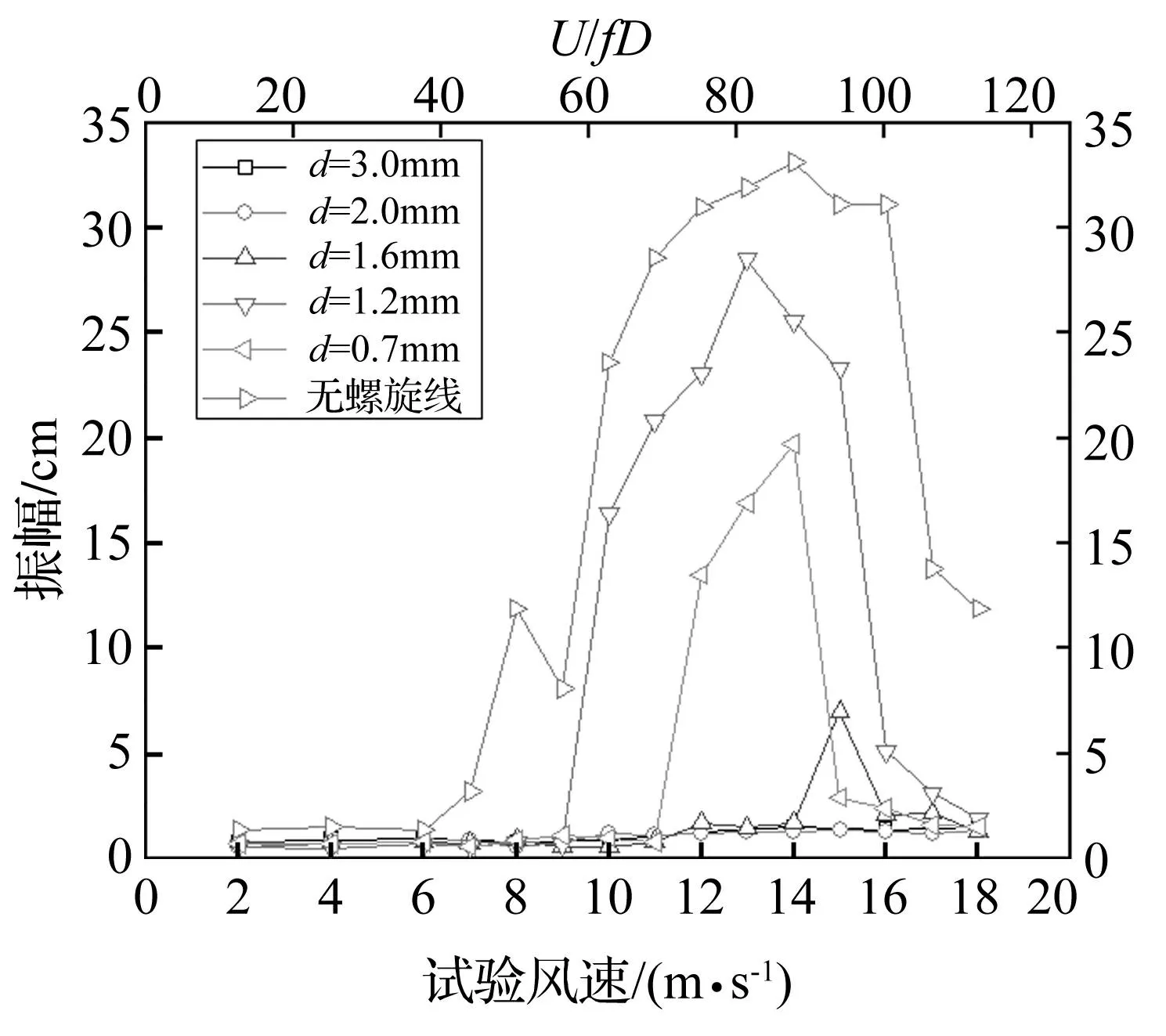
图8　螺旋线直径与振幅的关系(S=12D) Fig.8 Relation between helical line diameter and vibration control effect (S=12D)

由此结果可知，在螺旋线间距一定的情况下，只有其直径达到了一定的尺寸，才能达到较好的抑振效果。在直径1.6 mm以上时，没有观测到振动的发生。

固定螺旋线的直径d为1.2mm，改变螺旋线的间距，得到不同螺旋线间距下的振幅如图9所示。

由此结果可知，在螺旋线直径一定的情况下，加密螺旋线(即减小螺旋线的间距)能提高抑振效果。

图9　螺旋线间距与振幅的关系(d=1.2 mm) Fig.9 Relation between helical line space and vibration control effect (d=1.2 mm)

4螺旋线参数对气动力的影响

通过考察螺旋线的间距S、直径d可知，满足抑振效果的参数组合不止一种。在实际工程中选取这些参数的时候，附加螺旋线斜拉索的气动力是一个需要考虑的重要参数。在满足抑振效果的前提下，气动阻力最小的参数组合是最优的结果。

由于实际大跨度斜拉桥的设计基准风速较高，其对应的斜拉索雷诺数也较大，参考以前的研究结果[16-17]，本研究选取的试验雷诺数范围为20万~38万。

斜拉索的阻力系数为：

(1)

式中，CD为平均阻力系数；FD为单位长度上模型的平均气动阻力；ρ为空气密度(根据风洞内的温度、湿度、大气压强进行计算和修正)；U为来流风速；D为斜拉索模型的直径。

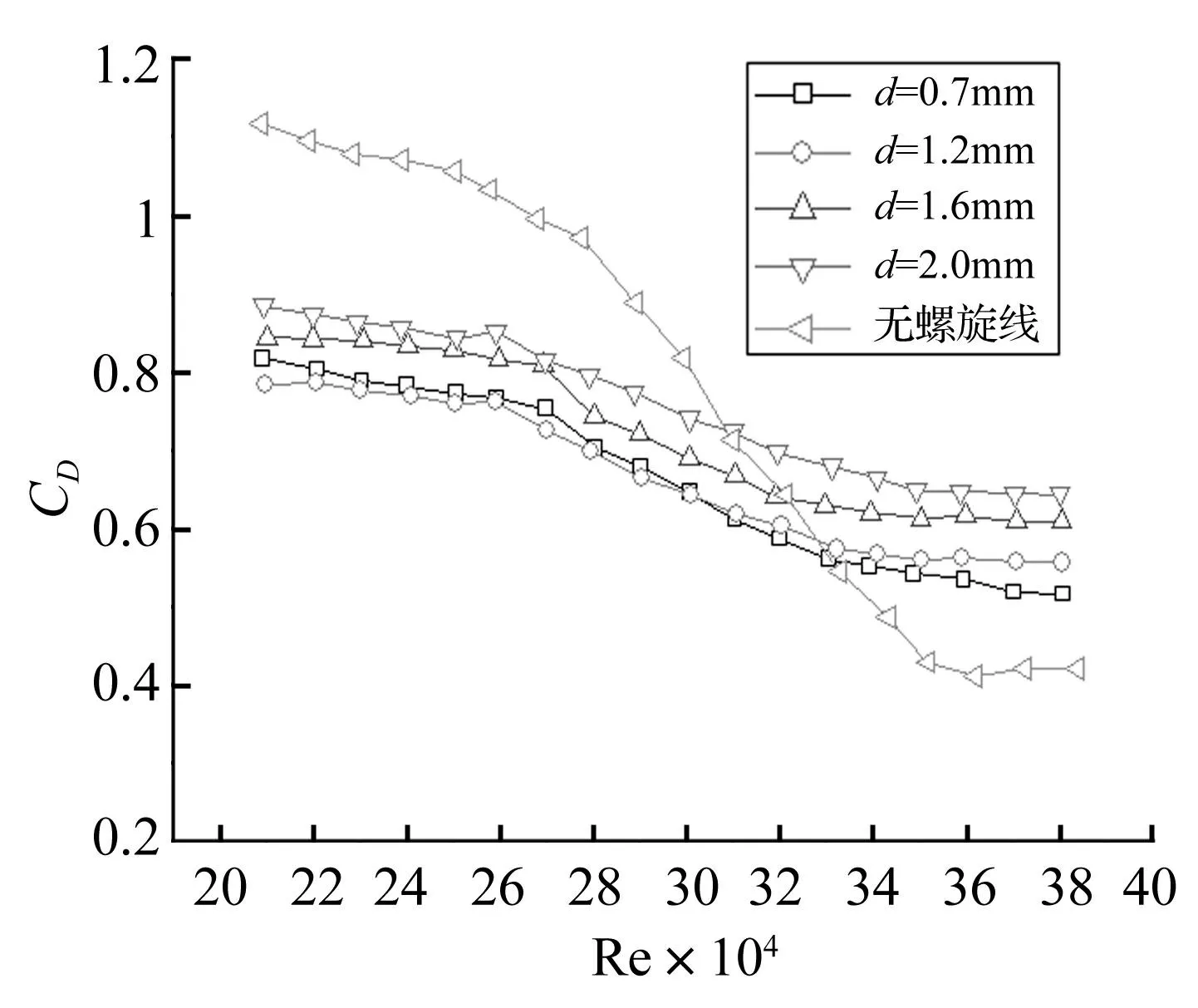
图10　不同螺旋线直径下阻力 系数随雷诺数的变化规律 Fig.10 Relation between Cd and Reynolds number with different helical line diameter

首先保持螺旋线的间距S=12D不变，改变螺旋线的直径d，得到阻力系数随雷诺数的变化如图10所示。

由图可知，作为整体的规律，在测试的螺旋线直径范围内，阻力系数基本随螺旋线直径的增大而增大；直径为0.7 mm和1.2 mm时，阻力系数的相对大小根据亚临界、临界和超临界雷诺数范围而发生了变化。

保持螺旋线的直径d=1.2 mm不变，改变螺旋线的间距，得到阻力系数随雷诺数的变化如图11所示。

图11　不同螺旋线间距下阻力系数随雷诺数的变化规律 Fig.11 Relation between Cd and Reynolds number with different helical line space

由结果可知，作为整体的规律，在测试的螺旋线直径范围内，在高雷诺数范围内，阻力系数基本随螺旋线间距的增大而减小；在低雷诺数范围内，阻力系数相对接近。

上述结论与文献[17]的变化规律基本一致。

5螺旋线优化参数的讨论

如前所述，实桥斜拉索的雷诺数较大，常处于临界雷诺数或超临界雷诺数[16]，因此从气动力角度考察螺旋线的直径时，应针对高雷诺数时的气动力进行考察。

针对本研究使用的D=155 mm的斜拉索，在考察的螺旋线直径(d=0.7 mm~2.0 mm)和间距(S=6D~12D)范围内，螺旋线直径d≥1.6 mm、间距为12D时基本能起到抑振效果。如果减小螺旋线的直径，如取d=1.2 mm，必须同时减小螺旋线的间距至6D(见图10)，才能达到抑振效果。可见，螺旋线的直径和间距成一定程度的正比关系。

在具有较好抑振效果的螺旋线直径和间距组合的区域，测试其阻力系数，具有最小阻力系数的组合将是最优的螺旋线参数。

上述讨论针对的是一个斜拉索直径的情况。将斜拉索直径作为参数，得到上述最优螺旋线参数与斜拉索直径的关系，是下一步值得研究的工作。

6结论

本文通过风洞试验，研究了斜拉索空间位置、降雨量、风速等对斜拉索风雨振的影响，选定振动最大时上述参数，研究了作为气动抑振措施的螺旋线的直径和在斜拉索上缠绕间距两个参数对抑振效果的影响，并研究了附加不同参数螺旋线时斜拉索的气动阻力系数随雷诺数的变化规律，提出了最优化螺旋线参数的选取原则，主要结论如下：

(1)针对本研究选定的D=155 mm的斜拉索，斜拉索的水平角β=35°、竖向角α=25°、较小的降雨强度(10 mm/h)、特定的风速范围(无量纲风速60~100m/s、风速10~16 m/s)的情况下发生的振动最为激烈。

(2)在选定螺旋线间距的情况下，随着螺旋线直径的增大，其抑振效果趋于显著。

(3)在选定螺旋线直径的情况下，随着螺旋线间距的减小，其抑振效果趋于显著。

(4)附加螺旋线斜拉索的气动阻力系数随螺旋线直径的增大或螺旋线缠绕间距的减小而增大。在超临界雷诺数区域，附加螺旋线时的阻力系数均大于无螺旋线时的阻力系数。

(5)在能够达到较好抑振效果的螺旋线参数组合中，取得最小气动阻力系数的组合为最优化的螺旋线设计参数。

参考文献

[1]Hikami Y, Shiraishi N. Rain-wind induced vibrations of cables in cable stayed bridge [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 29: 409-418.

[2]Matsumoto M, Shiraishi N. Rain-wind induced vibrations of cables in cable stayed bridge [J]. Journal of wind Engineering and Industrial Aerodynamics,1992, 43: 2011-2022.

[3]顾明, 刘慈军, 罗国强, 等. 斜拉桥拉索的风(雨)激振及控制[J]. 上海力学,1998, 19(4)：283-288.

GU Ming, LIU Ci-jun, LUO Guo-qiang, et al. Rain-wind induced vibration of cable on cable-stayed bridges and tts control [J]. Shanghai Journal of Mechanics,1998, 19(4)：283-288.

[4]Yamaguchi H. Anlytical study on growth mechanism of rain-vibration of cable [J]. Journal of Wind Engineering and Industrial Aerodynamics,1990, 33:73-80.

[5]Matsumoto M, Yagi T, Sakai S, et al. Steady wind force coefficients of inclined stay cables with water rivulet and their application to aerodynamics [J]. Wind & Structures,2005, 8(2) : 107-120.

[6]Matsumoto M, Yagi T, Goto M, et al. Rain-wind-induced vibration of inclined cables at limited high reduced wind velocity region [J]. Journal of Wind Engineering and Industrial Aerodynamics,2003, 91: 1-12.

[7]Cosentino N, Flamaned O, Ceccoli C. Rain-wind-induced vibration of induced stay cables. Part I：Experimental investigation and physical explanation [J]. Wind and Structure,2003, 6 (6):471- 484.

[8]李寿英，陈政清，顾明. 斜拉索风雨激振中拉索和水线之间的耦合运动[J]. 振动与冲击，2008, 27(10)：1-5.

LI Shou-ying, CHEN Zheng-qing, GU Ming.Coupled motion between stay cables and rivulets in rain-wind induced vibration [J]. Journal of Vibration and Shock, 2008, 27(10)：1-5.

[9]刘庆宽. 斜拉桥斜拉索风雨振时索表面水线摆动作用及规律的试验研究[J]. 土木工程学报，2007，40(7)，72-77.

LIU Qing-kuan. Experimental study on movement of water rivulet on cable surface in rain-wind induced vibration of stay-cables [J]. China Civil Engineering Journal， 2007，40(7)，72-77.

[10]刘庆宽, 乔富贵, 张峰. 斜拉索表面水线多相复杂摆动对索气动稳定性的影响[J]. 工程力学，2008，25(6)，234-240.

LIU Qing-kuan, QIAO Fu-gui, ZHANG Feng. Effect of non-uniform rivulet movement on rain-wind induced vibration of stay-cables [J]. Engineering Mechanics,2008，25(6)，234-240.

[11]Matsumoto M, Yagi T, Liu Q, et al. Effects of axial flow and Karman vortex interference on dry-state galloping of inclined stay-cables [C]// Proceedings of the 6th International Symposium on Cable Dynamics, Charleston, South Carolina, U.S.A., September 19-22, 2005, 247-254.

[12]杜晓庆，顾明. 斜置拉索表面脉动风力特性研究[J]. 振动与冲击. 2012，31(4)：139-144.

DU Xiao-qing, GU Ming.Characteristics of fluctuating forces on inclined stay cable [J]. Journal of Vibration and Shock, 2012，31(4)：139-144.

[13]刘庆宽, 张峰，马文勇，等. 斜拉索雷诺数效应与风致振动的试验研究[J]. 振动与冲击, 2011, 30(12): 114-119.

LIU Qing-kuan, ZHANG Feng, MA Wen-yong, et al. Tests for Reynolds number effect and wind-induced vibration of stay cables [J]. Journal of Vibration and Shock, 2011, 30(12): 114-119.

[14]裴岷山，张喜刚，朱斌，等. 斜拉桥的拉索纵桥向风荷载计算方法研究[J]. 中国工程科学, 2009, 11(3): 26-30.

PEI Min-shan, ZHANG Xi-gang, ZHU Bin, et al. Study on longitudinal wind load calculation method of cables for cable-stayed bridge [J]. Engineering Sciences, 2009, 11(3): 26-30.

[15]刘庆宽. 多功能大气边界层风洞的设计与建设[J]. 实验流体力学, 2011, 25(3): 66-70.

LIU Qing-kuan. Aerodynamic and structure design of multifunction boundary-layer wind tunnel [J]. Journal of Experiments in Fluid Mechanics, 2011, 25(3): 66-70.

[16]刘庆宽, 乔富贵, 张峰. 考虑雷诺数效应的斜拉索气动力试验研究[J]. 土木工程学报,2011, 44(11): 59-65.

LIU Qing-kuan. Aerodynamic and structuredesign of multifunction boundary-layer wind tunnel [J]. Journal of Experiments in Fluid Mechanics, 2011, 25(3): 66-70.

[17]李文勃，林志兴，杨立波. 超长斜拉索风阻系数及风雨激振的试验研究[J]. 振动、测试与诊断,2005，25(2): 85-90.

LI Wen-bo, LIN Zhi-xing, YANG Li-bo. Investigation ondrag coefficients and rain-wind induced vibration of extremely long stay cables in wind tunnel [J]. Journal of Vibration, Measurement & Diagnosis,2005，25(2): 85-90.