智能桁架结构最优振动控制与作动器优化配置

第一作者曹玉岩男，硕士，助理研究员，1986年2月生

智能桁架结构最优振动控制与作动器优化配置

曹玉岩，王志臣，付世欣,吴庆林

(中国科学院长春光学精密机械与物理研究所，吉林130033)

摘要：研究了智能桁架结构最优振动控制和作动器的优化配置问题。首先采用有限元方法，根据Hamilton原理推导了智能桁架结构的机电耦合动力学方程，根据线性二次型最优控制理论，推导了结构振动控制的数学模型，通过最小化性能泛函，求解黎卡提矩阵代数方程确定了最优控制输入。然后通过对最优控制性能指标函数的修正，得到了与初始状态无关的性能指标，以修正的性能指标为目标函数，应用模拟退火算法对作动器位置进行了优化配置。最后给出了空间智能桁架结构振动控制算例验证建模过程和算法。算例结果表明，通过最优振动控制可以使结构振动快速衰减，达到振动抑制的效果，而且通过模拟退火算法可以确定最佳的作动器布置方式。

关键词：智能桁架；Hamilton原理；振动控制；模拟退火

收稿日期：2013-11-08修改稿收到日期：2014-02-12

中图分类号:TP13文献标志码：A

Optimal vibration control and actuator placement for intelligent truss structures

CAOYu-yan,WANGZhi-chen,FUShi-xin,WUQing-lin(Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences,Changchun 130033, China)

Abstract:The optimal vibration control and actuator placement for intelligent truss structures was investigated. The mech-electric coupling dynamic formulation of piezoelectric intelligent truss structures based on Hamilton principle was presented. The mathematical model of vibration control for truss structures was derived using linear quadratic Gauss optimal control theory. The input of optimal control was determined by minimizing the performance function and solving the Riccati algebraic equation. Then, the performance criterion unrelated to initial state was obtained through correcting the performance criterion of optimal control. The optimization of actuator position was performed using simulated annealing algorithm so as to minimize the corrected performance criterion. The numerical example of vibration control for a spatial intelligent truss structure was given to verify the modeling process and optimization algorithm. The simulations results indicate that the vibration suppression effect is obvious and the vibration responses decrease quickly by the optimal vibration control.

Key words:intelligent truss; Hamilton theory; vibration control; simulated annealing

随着航天事业的发展，航天器朝着轻量化、大型化方向发展，桁架结构作为一种特殊的结构得到了越来越普遍的应用[1-2]。由于其自身低刚度、弱阻尼的特点，振动问题很突出，在很长一段时间内，桁架结构振动控制问题一直是研究的热点，尤其是压电陶瓷堆作动器的出现，使得复杂桁架结构主动振动控制成为可能[3]。将作动器和传感器与桁架结构结合一起形成自适应结构，在振动控制、噪声抑制、形状控制和精密定位领域具有广泛的应用前景。

在国内外，智能结构的振动主动控制及优化方法已经取得了一定的进展[1,4-6]，结构振动控制和作动器的最优布置一直是该领域研究的主要问题。Moita等[1]研究了压电层合板结构的振动控制问题，并采用模拟退火算法对贴片作动器的位置进行了优化配置。Yan等[7]研究了空间桁架结构的振动控制问题，作动器的优化配置采用遗传算法实现，但其优化结果受到初始条件的影响很大，不同的初始条件将得到不同的优化配置结果。徐亚兰等[8]基于结构模态空间范数研究了压电柔性结构振动控制问题。谢永等[9]对10跨桁架结构的动力特性和主动振动控制进行实验研究。曾光等[10]研究了基于遗传算法的空间智能桁架结构振动控制中的作动器/传感器位置优化问题。徐斌等[11]针对区间参数压电智能结构/控制一体化多目标拓扑优化问题，提出了一种区间参数结构/控制多目标拓扑优化方法。彭海军等[12]针对桁架结构的振动抑制问题，采用基于变形修正的物理降阶方法对有限元模型降阶，并设计线性二次高斯(LQG)最优控制律。赵国伟等[13]对柔性自适应桁架最优振动控制进行了实验研究。

本文研究了智能桁架结构最优振动控制和作动器的优化配置问题。首先采用有限元方法和最优控制理论，建立智能桁架结构最优振动控制模型，通过最小化性能泛函，并求解黎卡提(Riccati)矩阵代数方程确定了最优控制输入。然后应用模拟退火算法对作动器的位置进行优化。最后给出空间智能桁架结构的仿真算例，验证建模过程和算法。

1智能桁架结构最优振动控制系统建模

1.1智能桁架结构动力学建模

智能桁架结构的杆件包括压电作动器和主体杆件，其中压电作动器是由多层压电片堆叠胶合而成的，李东旭等[14-16]详细介绍了压电材料单元的力学方程，这里仅作简要叙述。作动器结构如图1所示，在电压的作用下可产生轴向伸缩位移，其动力学模型如图2所示。

图1　压电陶瓷堆作动器结构 Fig.1 Structure of piezoelectric actuator

图2　压电作动器力学模型简化 Fig.2 Mechanic model of piezoelectric actuator

根据Hamilton变分原理，轴向伸缩PZT压电元件机电耦合动力学方程为

(1)

式中：L=T-U为Lagrange函数，T为系统动能，U为系统势能，δ′W为外载荷所做虚功(外载荷所做功的变分)。

由式(1)可得压电作动器单元动力学方程为[16]

(2)

(3)

(4)

压电主动杆是由压电作动器两端与主体杆件连接而成的可轴向伸缩的杆件，结构如图3所示，其中单元1、3为主体材料单元，单元2为压电作动器单元。

图3　主动杆示意图 Fig.3 Diagram of active members

单元1、3的有限元方程为

(5)

式中，上标(h)表示主体杆件材料的相关矩阵，其含义与式(2)一致。

对单元1或3，其方程的具体形式为

(6)

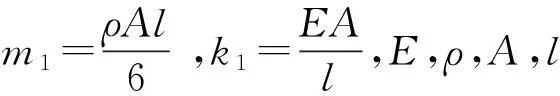
对单元1、2、3的质量矩阵和刚度矩阵进行组装，得到总体坐标系下结构动力学方程为

(7)

式中，上标(c)表示主动杆的相关矩阵。

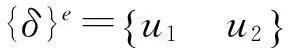
矩阵[H],[M]的表达式为

式中，λ=k1k2+k2k3+k1k3，ki(i=1,2,3)为单元i的拉伸刚度，kuv为作动器的耦合刚度。

将式(8)代入式(7)得到主动杆的机电耦合动力学方程为

[Kuv]e{δ}e+{Kvv}eφ=-{Q}e

(10)

通过缩聚变换，使压电主动杆的方程与主体杆单元具有相同形式。根据以上推导得到了压电主动杆件模型，通过坐标变换将各单元的质量矩阵和刚度矩阵变换为总体坐标系下的特性矩阵，然后对其进行组集，即得到压电桁架结构的无阻尼动力学方程为

(11)

式中，

1.2最优振动控制建模

由于桁架结构的特性矩阵如刚度矩阵、质量矩阵等均是时不变的，结构振动控制系统属于线性定常系统，根据最优控制理论，性能指标是状态变量的二次函数,可以把这种动态系统的最优控制问题视为线性二次型最优控制问题[17]。

为了应用线性二次型最优控制，将式(11)变换为状态空间方程表达式为

(12)

为了能在消耗最少控制能量的情况下使结构振动迅速衰减，根据线性二次型最优控制理论，性能指标函数表达为

(13)

式中，Q∈R2n×2n为半正定的状态加权矩阵，R∈Rr×r为正定控制加权矩阵，Q,R为对阵矩阵且常取为对角阵。

根据最优控制理论，使性能指标函数达到最小值的充分必要条件为

u(t)=-Kx(t)=-R-1BTPx(t)

(14)

矩阵P可以通过求解黎卡提(Ricatii)矩阵代数方程得到，即

ATP+PA+Q-PBR-1BTP=0

(15)

性能指标函数的最小值为

(16)

将式(14)代入式(12)得

(17)

由式(17)可求得

x=x0e(A-BR-1BTP)t

(18)

2压电作动器的优化配置

压电作动器的最优配置问题属于离散规划问题，有很多优化方法如遗传算法、模拟退火算法可以求解该问题，在这里采用模拟退火算法，与传统的应用梯度的优化方法相比，模拟退火算法的优点可以防止过早收敛与局部最优解。

2.1模拟退火算法

模拟退火算法于1982年由Kirkpatrick等引入组合优化领域，它源于对固体退火过程的模拟，采用Metropolis接受准则，并适当的控制温度的下降过程实现模拟退火，从而达到求解全局优化问题的目的。模拟退火算法中按Metropolis接受准则确定。

算法中是否接受从当前解x1到新解x2的转移由Metropolis接受准则决定，可以描述为

2.2作动器优化配置

根据线性二次型最优控制理论，最小化性能指标相当于最小化系统能量与控制能量，将式(18)和式(14)代入式(13)得

(20)

从式(20)可以看出性能指标函数与初始状态有直接关系，为了消除初始状态对优化结果的影响，将对能量函数做如下修正[18]，并将修正后的能量函数作为优化目标函数。假设系统的初始状态x0在n维单位球面上随机分布，则式(20)将变化为

(21)

式中，Aeq=A-BR-1BTP

Qeq=Q+(R-1BTP)TR(R-1BTP)

对式(21)计算关于初始状态x0的数学期望为

(22)

(23)

(24)

修正后的系统性能指标函数可以表达为

(25)

式(25)所表示的性能指标的意义为：当系统的初始状态x0在n维单位球面上随机分布时，最小化修正性能指标式(25)等价于最小化性能指标式(25)关于初始状态的数学期望。

根据上述推导，将修正的性能指标函数，即式(25)作为作动器优化配置的目标函数，可以建立作动器优化配置的数学模型为

(26)

式中，λj表示第j个杆件是否配置作动器，0-不安装，1-安装，n,m分别表示桁架杆件总数和作动器总数。

2.3算法中初始温度设置及新解构造

初始温度T0及降温准则将对算法的性能有很大影响，必须设置足够高，至少在初始时保证所有解都能被接受，这里采用多次随机布置产生一组变量，计算相应的目标函数值，利用这组目标函数的最大值与最小值之差来确定初始温度状态，即

(27)

式中，pr为初始接受概率。

(28)

3仿真算例

以如图4所示20节点64杆空间智能桁架结构为例，对其进行相应的仿真分析。桁架节点和单元编号如图4所示，约束1~4号节点的全部自由度，桁架结构共有16×3=48自由度。桁架结构几何参数和材料特性参数如表1所示。

表1　桁架中杆件及作动器相关参数

图4　空间桁架结构 Fig.4 Structure of truss

仿真验证三种情况：首先在每个杆件上均布置作动器，共64个作动器，分析最优控制前后结构振动衰减情况；然后通过分析布置10(1~64任取)个作动器情况下优化布置前后的控制效果，来验证优化配置算法；最后分析布置不同数量作动器情况，优化性能指标与作动器数目的关系。其中最优振动控制加权矩阵选取Q=106I,R=I。

3.1每个杆件均布置作动器情况

在每个杆件位置均布置作动器的情况下，共有64

个压电作动器，对三种不同的初始扰动条件进行了动态响应分析，并采用提出的方法进行最优振动控制。三种不同的初始扰动条件分别为：

结构自由振动响应和最优振动控制后的响应如图5所示。

从图5(a)~(c)中可以看出，通过最优振动控制可以使结构振动快速衰减，1s后衰减90%以上，1.5s后基本衰减为0。

3.2配置10个压电作动器情况

对个作动器的位置进行优化配置，采用模拟退火算法对其进行优化配置，并对优化配置前后最优振动控制的结果进行对比。优化求解参数如表2所示，优化过程中，优化前后个作动器布置位置如图6所示，目标函数变化如图7所示，新解接受与拒绝柱形图如图8所示，温度下降曲线如图9所示。

图5　布置64个压电作动器在三种工况下，智能桁架结构 最优振动控制前后节点位移动态响应，图(a)(b)(c)分别对应初始扰动条件(Ⅰ)(Ⅱ)和(Ⅲ) Fig.5　Dynamic responses of the intelligent truss structure without control and with optimal control by actuators for different initial disturbances, figures (a), (b) and (c) show the response for initial disturbance case (Ⅰ), (Ⅱ) and (Ⅲ) respectively

表2　优化求解参数

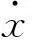
从图10(a)和(b)可以看出，优化配置前，20节点X向动态位移衰减很慢，衰减时间较长，1.5 s时还存在较大幅度的振动位移，而优化配置后，动态位移衰减很快，1 s内位移得到了很好的抑制。

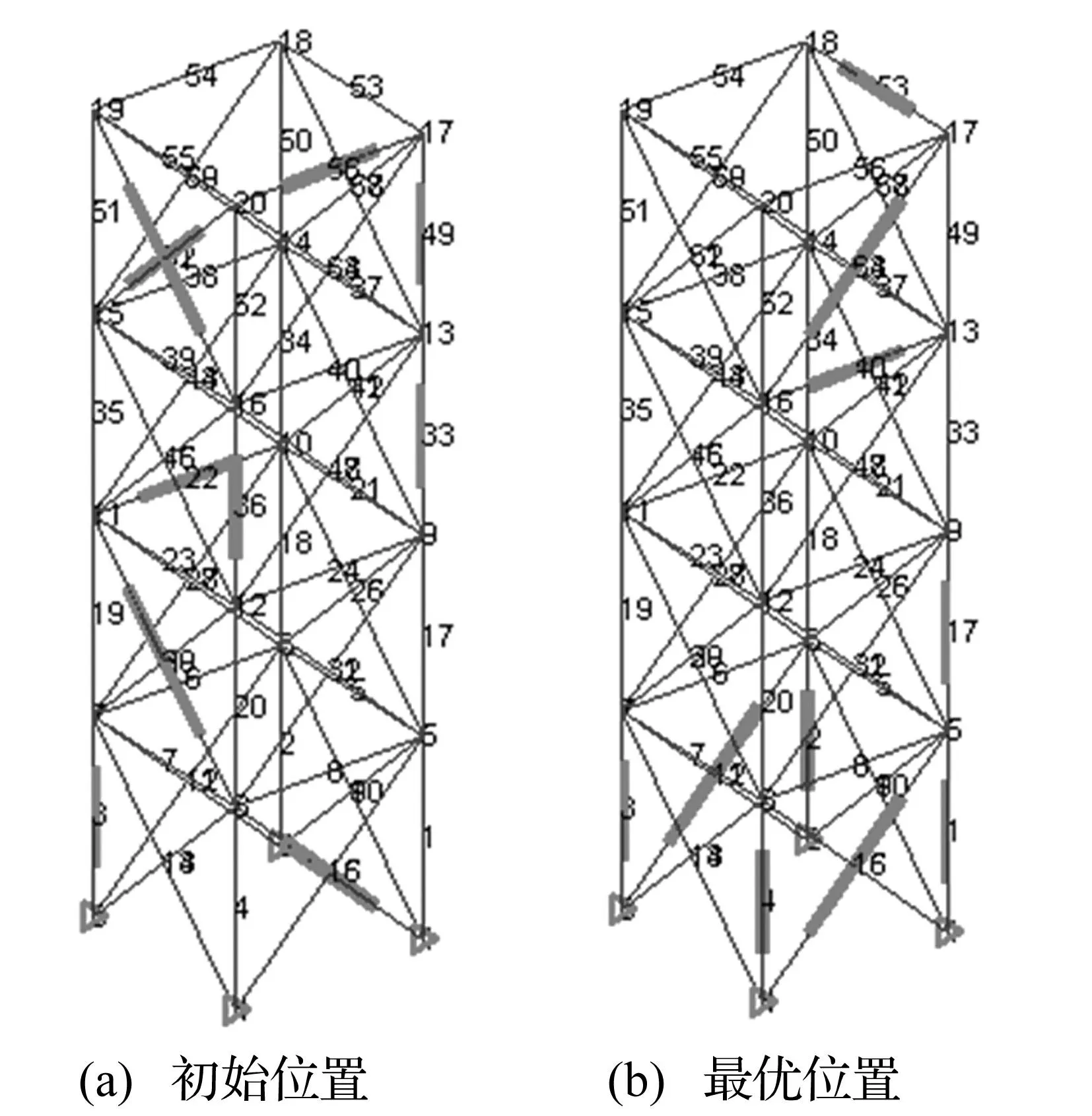
图6　优化配置前后10个作动器的位置 Fig.6 Initial and optimal locations for actuators

3.3配置不同数量作动器情况

为了研究作动器数目对控制性能的影响，对配置不同数目作动器的情况进行仿真分析，配置作动器数目为5~62，性能指标变化如图11所示。

从图11可以看出，随着作动器数目的增加，性能指标μ随之减小，控制总能量不断下降，即作动器越多控制性能越好。

从图11还可以看出，在作动器数目1~10阶段，目标函数下降速度较快，目标函数值减小70%以上，而在作动器数目17~62阶段，目标函数仅下降30%。由此可知，作动器数目存在一个临界值，在达到临界数目前，作动器数目的增加对控制性能影响较大，而超过临界数目后，对控制性能影响不明显。因此对桁架结构的振动控制，仅需配置很少一部分作动器就能达到理想的控制效果。

图7 优化配置10个作动器目标函数变化Fig.7Objectivefunctioncurveforoptimization图8 优化配置10个作动器接受与拒绝图Fig.8Acceptanceandrefusalcurveforoptimization图9 优化配置10个作动器降温曲线Fig.9Temperaturedescendcurveforoptimization

图10 优化配置前后20节点X向动态位移响应Fig.10Thedynamicdisplacementresponseofnode2direction图11 作动器数目与性能指标变化Fig.11Therelationsbetweenactuatornumbersandobjectionfunction

4结论

研究了智能桁架结构最优振动控制与作动器最优配置问题，首先采用有限元方法推导了智能桁架结构振动控制的数学模型，通过最小化性能泛函，求解黎卡提(Riccati)矩阵代数方程确定了最优控制输入。然后以修正的性能指标为目标函数，应用模拟退火算法对作动器位置进行了优化配置。最后给出了桁架振动控制算例验证建模过程和算法。

算例结果表明，(1)通过最优振动控制可以使结构振动快速衰减，能够达到很好的振动抑制效果；(2)对于确定相同数量的作动器，不同的布置方式控制效果差别很大，通过模拟退火算法优化，可以确定出最佳布置方式，使控制性能得到明显改善；(3)布置的作动器数量越多，控制效果越好，但作动器数目存在一个临界值，小于该临界值时，作动器数目的增加对控制性能的影响非常显著，大于该临界值时，作动器数目的增加对控制性能的影响不明显。

参考文献

[1]Moita J M S, Correia V M F, Martins P G, et al. Optimal design in vibration control of adaptive structures using a simulated annealing algorithm[J]. Composite Structures, 2006, 75(1):79-87.

[2]Muc A, Kedziora P. Optimal design of smart laminated composite structures[J]. Materials And Manufacturing Processes, 2010, 25(4):272-280.

[3]Irschik H. A review on static and dynamic shape control of structures by piezoelectric actuation[J]. Engineering Structures, 2002, 24(1):5-11.

[4]Frecker M I. Recent advances in optimization of smart structures and actuators[J]. Journal of Intelligent Material Systems And Structures, 2003, 14(4-5):207-216.

[5]Moita J S, Martins P G, Mota Soares C M, et al. Optimal dynamic control of laminated adaptive structures using a higher order model and a genetic algorithm[J]. Computers & Structures, 2008, 86(3-5):198-206.

[6]聂润兔, 邵成勋, 邹振祝. 智能桁架机电耦合动力分析与振动控制[J]. 振动工程学报，1997，10(2)：3-8.

NIE Run-tu, SHAO Cheng-xun, ZOU Zhen-zhu. Mech-electric coupling dynamic analysis and vibration control of intelligent truss structures[J]. Journal of Vibration Engineering, 1997, 10(2): 3-8.

[7]Yan Y J, Yam L H. Optimal design of number and locations ofactuators in active vibration control of a space truss[J]. Smart Materials and Structures, 2002, 11(4):496-503.

[8]徐亚兰, 陈建军. 空间范数在压电柔性结构振动控制中的应用研究[J]. 工程力学，2013，30(10)：1-4.

XU Ya-lan,CHEN Jian-jun. Researcn on vibration control of piezoelectric flexible structures based on spatial norms[J]. Engineering Mechanics, 2013, 30(10): 1-4.

[9]谢永, 赵童, 梁辰, 等. 桁架结构振动主动控制的实验研究[J]. 力学季刊，2010，31(4)：578-581.

XIE Yong, ZHAO Tong, LIANG Chen, et al. Experimental Study of Active Control for a Trussed Structure[J]. Chinese Quarterly of Mechanics, 2010, 31(4): 578-581.

[10]曾光, 李东旭. 空间智能桁架作动器/传感器位置优化中的遗传算法应用[J]. 宇航学报，2007，28(2)：461-464.

ZENG Guang, LI Dong-xu. Placement optimization of actuatorsPSensors of space intelligent truss using genetic algorithms[J]. Journal of Astronautics, 2007, 28(2): 461-464.

[11]徐斌, 赵普猛, 黎莹. 区间参数压电智能桁架结构/控制的多目标非概率可靠性拓扑优化[J]. 振动工程学报，2013，26(2)：169-177.

XU Bin, ZHAO Pu-meng, LI Ying. Multi-objective optimization for structural topology and control of piezoelectric smart truss with interval parameter considering non-probability reliability constraints[J].Journal of Vibration Engineering, 2013,26(2): 169-177.

[12]彭海军, 王文胜, 程耿东. 基于物理降阶模型的桁架结构振动主动控制[J]. 工程力学，2013，30(12)：1-7.

PENG Hai-jun,WANG Wen-sheng, CHENG Geng-dong. Active vibration control of a trussed structure based on the physical reduced model[J]. Engineering Mechanics, 2013, 30(12): 1-7.

[13]赵国伟, 黄海, 夏人伟. 柔性自适应桁架及其振动最优控制实验[J]. 北京航空航天大学学报，2005，31(4)：434-438.

ZHAO Guo-wei, HUANG Hai, XIA Ren-wei. Flexible adaptive truss testbed and its optimal control experiment for vibration[J]. Journal of Beijing University of Aeronautics and Astronautics, 2005, 31(4): 434-438.

[14]李东旭. 大型挠性空间桁架结构动力学分析与模糊振动控制[M]. 北京: 科学出版社, 2008.

[15]司洪伟. 大挠性航天桁架结构动力学建模及其主动模糊控制研究[D]. 长沙: 国防科学技术大学, 2006.

[16]龙连春. 智能桁架结构受力性态最优控制的建模与分析[D]. 北京: 北京工业大学, 2003.

[17]刘豹, 唐万生. 现代控制理论[M]. 北京: 机械工业出版社, 2006.

[18]Kleinman D L, Athans M. The Design of Suboptimal Linear Time-Varying Systems[J]. IEEE Transactions on Automatic Control, 1968, 13(2):150-159.