正交加筋圆柱壳-球壳组合结构自由振动分析

正交加筋圆柱壳-球壳组合结构自由振动分析

李正良，胡浩，于伟

(重庆大学土木工程学院，重庆400045)

摘要：研究不同边界条件下光滑、正交加筋圆柱壳-球壳组合结构的自由振动。通过对圆柱壳与球壳连接处简化处理，视球壳为自由约束，圆柱壳为简支约束，据Flügge薄壳理论利用Rayleigh-Ritz法求得结构频率，与有限元软件ANSYS结果比较，验证该方法的适用性及有效性；分析球壳扁率及组合壳体长径比对频率影响。结果表明，球心半角Φ增大结构自振频率降低；长径比L/Rc增大球心半角Φ对组合结构频率影响逐渐减弱，结构自振频率逐渐降低，且降幅减小。

关键词：加筋圆柱壳-球壳组合结构；Flügge理论；Rayleigh-Ritz法；自由振动

中图分类号:TB123文献标志码：A

Free vibration of joined and orthogonally stiffened cylindrical-spherical shells

LIZheng-liang,HUHao,YUWei(College of Civil Engineering, Chongqing University, Chongqing 400045, China)

Abstract:The free vibration of a joined, smooth and orthogonally stiffened cylindrical-spherical shell under various boundary conditions was studied.Based on the simplification of the joined part, the spherical shell is of free boundary condition and the cylindrical shell is of simply supported boundary condition. The Rayleigh-Ritz method was applied to solve the natural frequencies of the structure according to the Flügge’s thin shell theory. The natural frequencies were calculated and compared with those by the finite element software ANSYS to confirm the applicability and validity of the simplification. The effects of the shallowness of the spherical shell and the length-to-radius ratio of the joined shell on the free vibrational behavior of the joined structure were investigated. The results indicate that as the semi-angle Φ of the sphere increases, the natural frequencies decrease. As the length-to-radius ratio L/Rc increases, the influence of the semi-angle Φ of the sphere on the natural frequencies decreases, the natural frequencies decrease gradually and their reducing magnitude descends.

Key words:stiffened and joined cylindrical-spherical shell; Flügge’s theory; Rayleigh-Ritz method; free vibration

组合壳体结构广泛用于航天器、导弹、压力容器、潜艇及建筑等结构中。虽对圆柱壳[1-4]、加筋圆柱壳[5-8]及球壳[9-11]的振动特性已有诸多研究，但对组合壳体结构分析较少，尤其对加筋组合壳体的研究分析更少。

Saunders[12]用Rayleigh-Ritz法获得圆锥壳-球壳组合结构的自振频率，与试验结果对比表明吻合较好。Galletly等[13]用有限差分及有限元等数值方法研究一端固定，一端有不同封盖(如圆锥壳、半球壳、椭圆壳等)圆柱壳组合结构的自振频率。Yim等[14]研究一端固定一端自由且在轴向任意位置带圆板的圆柱壳自振特性。Lee等[15]通过简化圆柱壳-半球壳组合结构，在半球壳与圆柱壳连接处视半球壳为自由约束，圆柱壳为简支约束，据Flügge薄壳理论用Rayleigh-Ritz法获得不同边界条件下圆柱壳-半球壳组合结构的频率方程，将计算结果与试验及有限元分析对比表明，结果吻合较好。Yusefzad等[16]进一步分析两端自由约束半球壳-圆柱壳-半球壳预应力组合壳体的自振特性，与试验及有限元结果对比表明吻合较好。Qu等[17]用改进的变分法研究不同边界条件下带环向加劲肋的圆锥壳-圆柱壳-半球壳组合壳体自振特性，分析加劲肋分布及尺寸对结构自振频率影响。Kouchakzadeh等[18]用幂级数位移形式、据Donnell扁壳理论用Hamilton原理推导出正交铺设层合圆锥壳组合壳体的动力方程及连续性条件，分析圆锥半顶角、子午线长度及壳体厚度对组合结构自振频率影响。

本文在已有研究成果基础上，分别计算不同边界条件下、不同L/Rc值及不同扁率时光滑、正交加筋圆柱壳-球壳组合结构自振频率；分析L/Rc及扁率对两种组合结构自振频率影响，并与有限元ANSYS结果对比，证明该简化方法的有效性及适用范围。

1理论分析

本文讨论的加筋圆柱壳-球壳组合结构见图1。其中L为圆柱壳长；Rc为半径；h为厚度。Rp为球壳曲率半径；Φ为球心半角；t为厚度；ρ为材料密度；ν为泊松比；E为弹性模量；G为剪切模量；hs，hr分别为纵向、环向加劲肋高度；宽度为br，bs。

球壳本身自由振动中弯曲应变能占主要部分，薄膜应变能占比较小，球壳主要发生横向振动[20]。设球壳对组合结构频率影响较小且在圆柱壳与球壳连接处，球壳对圆柱壳约束较强，对光滑圆柱壳-球壳组合结构及正交加筋圆柱壳-球壳组合结构在球壳与圆柱壳连接处简化处理，视球壳为自由约束，圆柱壳为简支约束，分别求得二者动、势能，利用Rayleigh-Ritz法求解该组合结构在固定-自由及简支-自由边界条件下的自振频率，并与有限元结果对比，证明简化方法的合理性及有效性。

据Flügge薄壳理论，应变位移关系[19]为

(1)

圆柱壳应变能为

(2)

圆柱壳动能为

(3)

任意边界条件下圆柱壳振动位移函数设为

(4)

式中：A，B，C为振幅；m，n为轴向、周向波数；ω为固有圆频率；uc，vc，wc分别为轴向、环向、径向位移；φm(x)为特征梁函数，见文献[15]。

纵横向加劲肋、质心位移分量为

(5)

纵向加劲肋轴向应变为

(6)

环向加劲肋周向应变为

(7)

纵向加劲肋应变能为

(8)

环向加劲肋应变能为

(9)

式中：Ns，Nr，Ask，Ark，GJsk，GJrk分别为纵向、环向加劲肋数量、第k根加劲肋截面积及扭转刚度。

纵向加劲肋动能为

(10)

环向加劲肋动能为

(11)

球壳壳体中面曲率为

(12)

据无薄膜力理论，球壳应变能为

(13)

球壳动能为

(14)

自由边界条件下球壳位移分量设为

(15)

式中：D为振幅；up，vp，wp分别为轴向、环向、径向位移。

能量函数为

Π=Uc,max-Tc,max+Us,max-Ts,max+

Ur,max-Tr,max+Up,max-Tp,max

(16)

式中：Umax，Tmax分别为结构最大应变能、最大动能。

利用Rayleigh-Ritz法，取函数Π关于参数A、B、C、D的极值，得联立方程为

(17)

由式(17)可导出振动特征方程，用于确定加筋组合壳体结构的固有频率及模态。

(18)

式中：aij取决于结构参数及两端边界条件。

由矩阵对应行列式为零可得频率方程。

2数值算例及有限元分析

2.1ANSYS分析模型建立

结构参数为：E=210 GPa，ρ=7 850 kg/m3，Rc=175 mm，t=h=2.2 mm，hs=hr=6 mm，br=bs=3 mm，Ns=20，Nr=15，ν=0.3。在ANSYS有限元模型中，加劲肋采用Beam188单元考虑其拉压、弯曲及扭转；模型中球壳及圆柱壳为弹性薄壳，不计入剪切变形，故采用Shell63单元。光滑组合结构有限元模型共3 528个单元，3 856个节点；正交加筋组合结构有限元模型共9 972个单元，13 563个节点。三维ANSYS有限元模型见图2。

图2　三维有限元模型 Fig.2 ANSYS model of 3D

2.2球壳扁率对组合壳体频率影响及简化方法适用范围

所求简支-自由边界条件下不同L/Rc值、不同球心半角的光滑圆柱壳-球壳组合结构自振频率见图3。其中Ritz为由式(18)所得结构自振频率，FEM为ANSYS有限元分析所得结构自振频率；Φ为球心半角，H/Rc=(1-cosΦ)/sinΦ为扁率，m、n见式(4)。Φ=0°及90°分别表示圆柱壳顶部为圆板(H/Rc=0)及半球壳(H/Rc=1)。由图3看出，球心半角Φ=0°～60°时，除n=2、3对应的频率值随Φ变化有较大波动外，其它n值对应的频率变化幅度均较小。总体看来，组合结构各阶频率值随球心半角Φ增大而减小，主要因Φ增大顶部球壳刚度降低，球壳对圆柱壳约束减弱。

图4为在简支-自由边界条件下，简化方法与有限元分析所得频率值进行误差分析比较结果。由图4(b)看出，m=2时简化方法所得各阶频率与有限元分析频率值相差较大，均在10%以上，此时L/Rc较小，球壳相对圆柱壳刚度较小，连接处球壳对圆柱壳约束减弱，导致简化方法误差较大。Φ=0°～60°，L/Rc≥1.0时，除图4(c)中n=2、3及图4(d)中n=2对应的频率值误差曲线，各阶频率值误差均在-5%～10%之间，为实际土木工程允许范围，表明简化方法具有足够精确性。而随Φ增大误差绝对值|Error|逐渐上升，尤其Φ= 90°时误差最大，表明半球壳对圆柱壳的约束最弱，此时简化方法不适用。随L/Rc增大误差整体降低，表明球壳球心半角即扁率对组合结构的频率影响逐渐减弱。误差Error计算式为

(19)

式中：fR为由Rayleigh-Ritz法所求各阶频率；fF为由有限元分析所得各阶频率。

图3　简支-自由边界条件下组合结构固有频率 Fig.3 Natural frequencies of a joined shell for simply supported-free boundary condition

图4　简支-自由边界条件下组合结构固有频率误差 Fig.4 Error of natural frequencies on a joined shell for simply supported-free boundary condition

计算的固定-自由边界条件下、不同L/Rc值、不同球心半角，光滑圆柱壳-球壳组合结构自振频率见图5，球心半角Φ对组合结构各阶频率影响与图3类似。

固定-自由边界条件下，简化方法与有限元分析所得频率值的误差分析比较见图6。由图6(b)、图6(d)、(f)、(h)可知，Φ=0°～60°时，除图6(f)中m=2、3及图6(h)中n=2对应的频率值误差大于10%外，结构各阶频率误差均较小。由图6 (a)、(c)、(e)、(g)可知, 随L/Rc增大各阶频率值误差先增大后减小，Φ=90°时误差仍最大。由于边界条件变化，与图4不同，Φ=0°～60°、L/Rc≤0.5及L/Rc≥4.0时，简化方法可获得较精确的计算结果。

作为比较，本文进一步分析简支-自由及固定-自由边界条件下带纵横向加劲肋的圆柱壳-球壳组合结构自振频率，见图7～图10。

图7与图3、图5类似，随Φ增大加筋组合结构各阶频率逐渐降低，随L/Rc增大降低幅度减小。L/Rc= 4.0时球心半角Φ对结构频率的影响可忽略。与光滑结构相比，加筋圆柱壳刚度更大，球壳对组合结构频率影响更小。

对加筋组合结构，在简支-自由边界条件下，计算简化方法与有限元分析频率值误差见图8。由图8看出，Φ=0°～60°范围内，随L/Rc降低误差减小。由于加筋肋的作用，尽管球壳相对柱壳刚度小，但加筋肋在球壳与圆柱壳连接处对圆柱壳约束较强，故简化方法的误差亦较小，满足工程要求。L/Rc≤2.0、Φ=0°～60°时除n=2、3的频率值误差曲线波动较大外，各阶频率值误均较小。可见简化方法能取得较好的频率值近似。L/Rc=4.0时，除n=2、3误差值曲线随Φ增大上升外，其它各阶频率值误差变化均较小。Φ=0°～60°范围内，各阶频率误差值曲线趋于平行，与图7相同，即L/Rc较大时Φ对结构频率的影响可忽略。

图5　固定-自由边界条件下组合结构固有频率 Fig.5 Natural frequencies of a joined shell for clamped-free boundary condition

图6　固定-自由边界条件下组合结构固有频率误差 Fig.6 Error of natural frequencies on a joined shell for clamped-free boundary condition

图7　简支-自由边界条件下加筋组合结构固有频率 Fig.7 Natural frequencies of a stiffened and joined shell for simply supported-free boundary condition

图8　简支-自由边界条件下加筋组合结构固有频率误差 Fig.8 Error of natural frequencies on a stiffened and joined shell for simply supported-free boundary condition

图9分析结果与图7类似，即随Φ增大加筋组合结构各阶频率逐渐降低；随L/Rc增大降幅减小。L/Rc=4.0时球心半角Φ对结构的频率影响可忽略。

图10分析结果与图6类似，由图10 (b)、(d)、(f)看出，Φ=0°～60°时，除图10(f)中m=2、3对应频率值误差大于10%外，结构各阶频率误差均在10%内。由图10 (c)、(e)、(g)看出,各阶频率值误差均较大，Φ=90°时误差仍最大。由于边界条件变化，与图8不同，Φ=0°～60°、L/Rc≤0.5时，表明该方法可获得较精确结果。

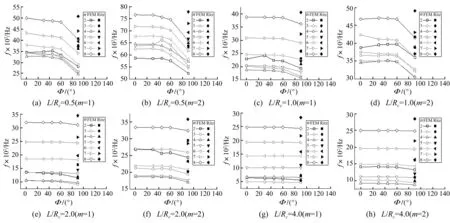
图9　固定-自由边界条件下加筋组合结构固有频率 Fig.9 Natural frequencies of a stiffened and joined shell for clamped-free boundary condition

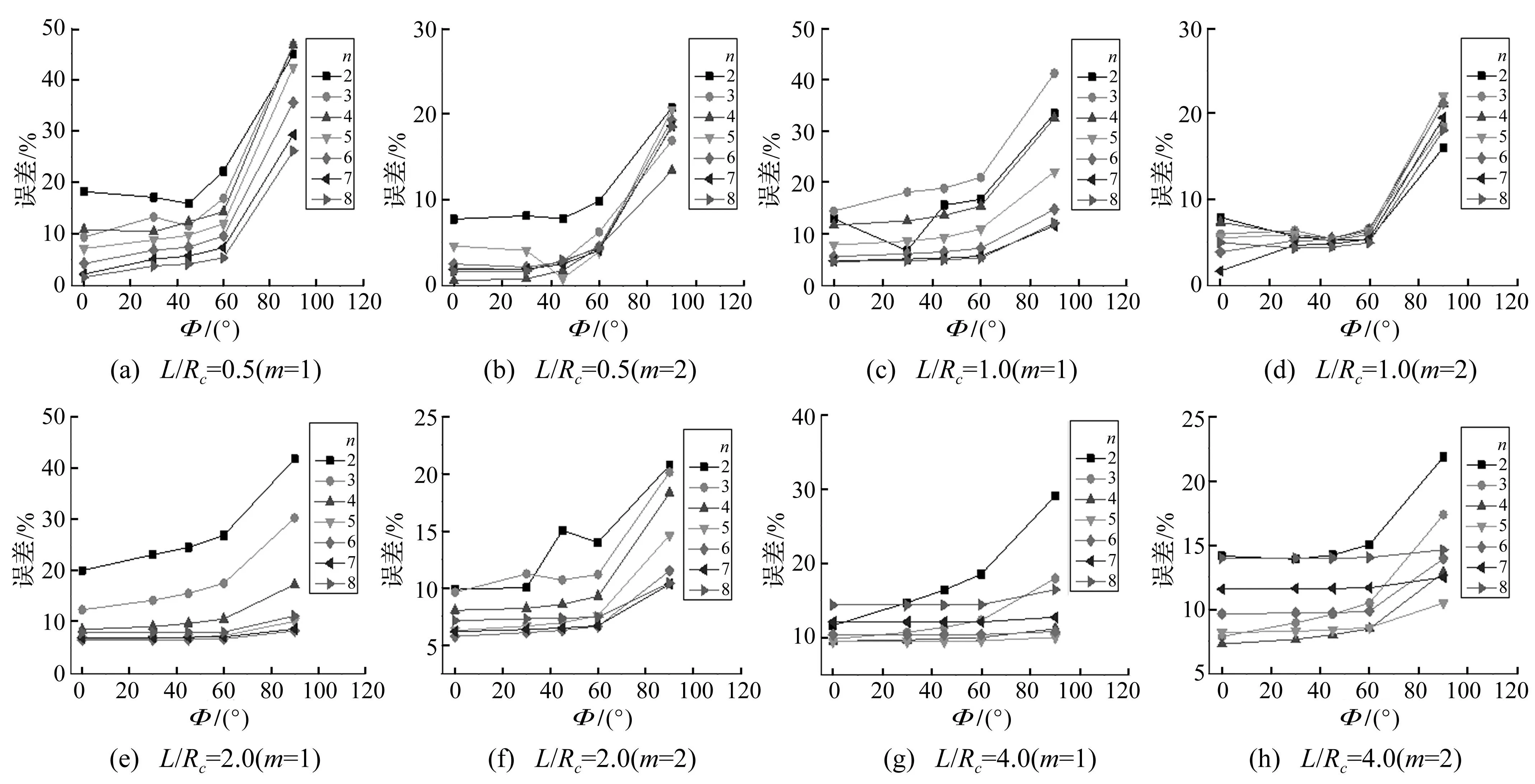
图10　固定-自由边界条件下加筋组合结构固有频率误差 Fig.10 Error of natural frequencies on a stiffened and joined shell for clamped-free boundary condition

2.3 简化方法与已有结果比较

为证明本文简化方法的适用性及有效性，与文献[13]中表8、表11结果进行对比，见表1 (L/Rc=1.0,h/Rc=0.002,ν=0.2)、表2(L/Rc=2.0,h/Rc=0.02,ν=0.2)。由表1可知，Φ=42°时本文方法所得误差较小，在10%内，满足工程误差要求。Φ=90°时频率误差值较大，简化方法不适用。由表2可知，此时L/Rc增大，仅n=5时误差较小，与图6(e)中n=3、4、5时类似。故对固定-自由约束的光滑组合结构，简化方法计算L/Rc=2.0的结构不适用。

由以上分析知，对于部分光滑和加筋组合球壳-圆柱壳结构，满足一定长径比及球心半角时，均可用本文简化方法计算结构固有频率，且简单实用。

表1　固定-自由边界条件组合结构频率对比分析

注：表中频率值对应m=1，括号数值为Φ=90°的频率误差值，Φ=42°为文献[13]中Rs/D=0.75对应的准球壳-圆柱壳组合结构。

表2　固定-自由边界条件组合结构频率对比分析

注：表中频率值对应m=1，括号数值为Φ=90°的频率误差值，Φ=42°为文献[13]中Rs/D=0.75对应的准球壳-圆柱壳组合结构。

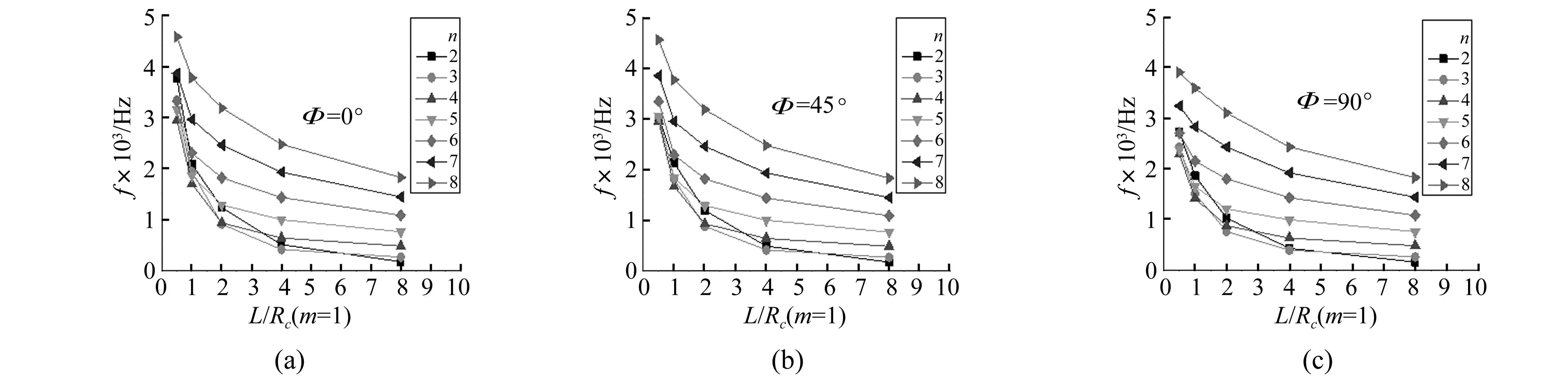
图11　简支-自由边界条件下不同L/R c时固有频率 Fig.11 Fundamental frequencies with different L/R cratios for simply supported-free boundary condition

图12　固定-自由边界条件下不同L/R c时的固有频率 Fig.12 Fundamental frequencies with different L/R cratios for clamped-free boundary condition

2.4长径比对加筋组合壳体频率影响

简支-自由与固定-自由边界条件下球心半角Φ=0°、45°、60°时，加筋组合结构各阶固有频率随L/Rc值增大的变化见图11、图12，此时m=1。由两图看出，随L/Rc增大各阶频率值都逐渐降低，且下降幅度减小，主要因L/Rc较大时结构较柔软，频率值不再随其变化有较大改变。对同一球心半角Φ，L/Rc≥2.0且n≥4时，随L/Rc与n同时增大，尽管边界条件不同，各阶频率值分别趋于相等，表明边界条件对高阶频率影响逐渐降低。

3结论

通过对光滑圆柱壳-球壳及正交加筋圆柱壳-球壳等组合结构进行自振分析，结论如下：

(1)球心半角Φ增大结构自振频率降低；L/Rc增大球壳球心半角即扁率对组合结构频率影响逐渐减弱。

(2)简支-自由边界条件下，对光滑组合结构，Φ=0°～60°、L/Rc≥1.0时简化方法结果精度较高；对加筋组合结构，Φ=0°～60°、L/Rc≤2.0时简化方法结果精度较高。

(3)固定-自由边界条件下，对光滑组合结构，Φ=0°～60°、L/Rc≤0.5及L/Rc≥4.0时简化方法结果精度较高；对加筋组合结构，Φ=0°～60°、L/Rc≤0.5时简化方法结果精度较高；Φ=90°时简化方法不适用。

(4)L/Rc值对组合结构固有频率影响显著，L/Rc增大，结构固有频率逐渐降低，且降幅减小。

参考文献

[1]Love A E H. A treatise on the mathematical theory of elasticity(Forth Edition )[M]. Dover Publication, 1944.

[2]Arnold R N, Warburton G B. Flexural vibrations of the walls of thin cylindrical shells having freely supported ends[J]. Proceedings of the Royal Society of London,Series A, 1949, 1049 (197):238-256.

[3]Forsberg K. Influence of boundary conditions on the modal characteristics of thin cylindrical shells[J]. American Institute of Aeronautics and Astronautics, 1964,12(2): 2150-2157.

[4]Haft E E. Natural frequencies of clamped cylindrical shells[J].American Institute of Aeronautics and Astronautics, 1968,6(4): 720-721.

[5]Galletly G D. On the in-vacuo vibrations of simply supported, ring-stiffened cylindrical shells[J]. Journal of Applied Mechanics-transactions of the ASME,1954,21(3):225-231.

[6]Egle D M. An analysis of free vibration of orthogonally stiffened cylindrical shells with stiffeners treated as discrete elements[J]. American Institute of Aeronautics and Astronautics,1968,6(3): 518-526.

[7]Mustafa B A J, Ali R. An energy method for freevibration analysis of stiffened circular cylindrical shells[J]. Computers and Structures,1989,32(2):355-363.

[8]Zhao X, Liew K M, Ng T Y. Vibrations of rotating cross-ply laminated circular cylindrical shells with stringer and ring stiffeners[J]. International Journal of Solids and Structures,2001,39(2):529-545.

[9]Kalnins A. On vibrations of shallow spherical shells [J]. Journal of the Acoustical Society of America,1961,33(8):1102-1107.

[10]Robinson A R. A numerical method for analysis of free vibration of spherical shells[J]. American Institute of Aeronautics and Astronautics,1967,5(7): 1256-1261.

[11]Pavlyuk N F, Kichaev Y P. Vibrations of a shallow spherical shell with a hole[J]. International Applied Mechanics,1971,7(3): 256-259.

[12]Saunders H. Inextensional vibrations of a sphere-cone shell combination[J]. Journal of the Acoustical Society of America, 1959,31(5):579-583.

[13]Galletly G D, Mistry J. The free vibrations of cylindrical shells with various end closures[J]. Nuclear Engineering and Design,1974,30(2):249-268.

[14]Yim J S, Lee Y S, Sohn D S. Free vibration of clamped-free circular cylindrical shell with a plate attached at an arbitrary axial position[J]. Journal of Sound and Vibration, 1998, 213(1):75-88.

[15]Lee Y S,Yang M S,Kim H S, et al. A study on the free vibration of the joined cylindrical-spherical shell structures[J]. Computers and Structures,2002,80(27/28/29/30): 2405-2414.

[16]Yusefzad M, Bakhtiarinejad F. A study on the free vibration of the prestressed joined cylindrical-spherical shell structures [J]. Applied Mechanics and Materials,2013,390:207-214.

[17]Qu Ye-gao, Wu Shi-hao, Chen Yong, et al. Vibration analysis of ring-stiffened conical-cylindrical-spherical shells based on a modified variational approach[J]. International Journal of Mechanical Sciences,2013,69:72-84.

[18]Kouchakzadeh M A,Shakouri M. Free vibration analysis of joined cross-ply laminated conical shells[J]. International Journal of Mechanical Sciences,2014,78:118-125.

[19]Flügge. Stresses in shells[M]. Berlin:Spring, 1962.

[20]Kalnins A. Effect of bending on vibrations of spherical shells [J]. Journal of the Acoustical Society of America, 1964,36(1): 74-81.