传动柔性及负载变化弹药传输机械臂位置控制及柔性振动抑制
传动柔性及负载变化弹药传输机械臂位置控制及柔性振动抑制
郭宇飞1,2,侯保林2
(1.武汉科技大学机械自动化学院,武汉430081;2.南京理工大学机械工程学院,南京210094)
摘要:针对现有坦克自动装弹机无法实现任意角度装填问题,设计出两自由度的弹药传输机械臂。研究考虑链条、转铰柔性且负载变化情况弹药传输机械臂位置控制与柔性振动抑制。将链条与转铰简化为线性无惯量弹簧,采用第二类Lagrange方法建立弹药传输机械臂刚柔耦合动力学模型。基于奇异摄动技术设计系统混合控制策略,柔性振动抑制采用速度反馈控制;刚性部分大范围运动采用基于隐式Lyapunov函数的连续时变增益PD控制,控制器增益为系统状态变量的可微函数,随系统状态变量逐渐趋向于零,增益逐渐趋于无穷大,而控制力始终保持在有界范围内。仿真结果显示,该混合控制器能克服负载变化及柔性振动影响,实现弹药传输机械臂点到点位置控制及柔性振动抑制,具有较强的鲁棒性。
关键词:弹药传输机械臂;传动柔性;负载变化;位置控制;振动抑制
中图分类号:Tp12;Tp13.3文献标志码:A
基金项目:国家自然科学
收稿日期:2014-07-09修改稿收到日期:2014-11-06
Positioning control and elastic vibration suppressing of an ammunition transfer manipulator with transmission flexibility and payload uncertainty
GUOYu-fei1,2,HOUBao-lin2(1. College of Mechanical Automation, Wuhan University of Science and Technology, Wuhan 430081, China;2. School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)
Abstract:The positioning control and elastic vibration suppressing of a novel 2-DOF ammunition transfer manipulators were analysed in consideration of joint chain flexibility and payload uncertainty. Regarding the joint and chain’s elasticity as a non-inertial spring, a dynamic model of the manipulator was derived via Lagrange method. Based on the singular perturbation method, the model was decomposed into two part, a fast subsystem and a slow subsystem. For the fast subsystem, a velocity difference feedback controller was proposed to suppress the elastic vibration. For the slow subsystem, a PD controller with continuous time-varying gains was designed based on a given implicit Lyapunov function. The controller’s gains, which are continuous-differentiable functions of the state, increase and tend to infinity as the system approaches the original state, but the control force always satisfies the given constraint. The simulation results demonstrate that the controller greatly compensates the effects of transmission flexibility and payload uncertainty, fulfills the accurate point to point control of the ammunition transfer manipulator, and is of good robustness.
Key words:ammunition transfer manipulator; transmission flexibility; payload uncertainty; positioning control; vibration suppressing
弹药传输机械臂作为坦克自动装弹机重要组成部分,安装于坦克车体内弹药仓与炮尾之间,负责将弹药协调到炮尾待装填位置,称为弹药协调器[1]。传统弹药协调器为单自由度机械臂结构,无法实现弹药任意角度装填[2]。本文设计的两自由度弹药传输机械臂,兼有任意角度协调及抓取、推送弹药功能。
作为坦克自动装弹机的重要组成部分,弹药传输机械臂朝轻量化方向发展。因此,结构设计、控制动力学分析阶段须考虑系统柔性影响。本文主要研究弹药传输机械臂传动关节的柔性。来自驱动部件、传动部件与传感器(如电机输出轴、谐波减速器、传动链/带、力矩传感器等)的结构柔性会产生系统谐振,严重影响机械臂的运动精度及控制稳定性。
Spong[3]对柔性关节机器人通过大量研究,率先建立柔性关节机械臂动力学模型,将柔性转动关节简化为线性扭簧。该模型基于关节弱柔性假设,适用于关节柔性力远大于电机驱动力的一类机器人。可采用力矩负反馈PD控制策略对柔性关节振动进行主动抑制。该控制策略需较高质量关节力矩信号及鲁棒性较好的力矩控制器[4-5]。郭闯强等[6]设计的轮辐式力矩传感器,结合名义输出力矩前馈补偿器,可实现系统柔性振动快速抑制。也可引入不同时间尺度,将系统分解为慢、快时变子系统,用混合控制方法进行系统位置控制与柔性振动抑制,即奇异摄动方法。可选择关节弹性力作为快时变变量,也可选择电机输出轴与机械臂本体角度差作为快时变变量。慢时变子系统控制器可选任何适用刚体机器人的控制策略,如自适应控制[7]、神经网络控制[8]、非奇异模糊Terminal滑模控制[9]等。快时变子系统控制器一般选速度反馈控制、最优控制[10]等控制策略。
针对文献[3]模型中未考虑参数不确定、摩擦、阻尼、简化扭簧刚度时变等非线性因素,赵志刚等[11]作进一步研究,建立更完整的柔性关节机械臂动力学模型。陈健康等[12]针对柔性关节非线性摩擦特性,提出基于H∞鲁棒原理的控制策略,在频域范围内分析摩擦的描述函数。党进等[13-14]针对柔性关节中存在的摩擦力及不确定扰动,提出由前馈补偿器结合反馈补偿器、模糊滑模控制器的鲁棒控制策略。Chaoui等[15]采用自适应二型模糊控制策略,研究考虑参数不确定、非线性摩擦力的关节柔性机械臂轨迹跟踪控制。计算结果显示二型模糊控制律较一型鲁棒性更强。
本文针对两自由度弹药传输机械臂,考虑链传动、转动关节柔性及负载变化影响,建立刚柔耦合动力学模型;利用奇异摄动技术引入双时间尺度,将系统分解为快、慢时变子系统;对两子系统分别采用速度差值反馈控制及隐式Lyapunov函数时变增益PD反馈控制律[16-17],研究弹药传输机械臂点到点的位置控制及柔性振动抑制。
1弹药传输机械臂模型
1.1结构原理与动力学建模
弹药传输机械臂三维模型见图1,结构原理见图2。该结构由安装架、升降部分与翻转部分组成。安装架固定在车体内,位于炮尾与弹药仓之间;升降部分采用双链传动,两主动链轮同轴固定且由同一电机驱动;升降部分固定在紧边链条上,可沿导轨上下滑动;翻转部分由电机通过减速器、转向器驱动,可360°翻转,兼有抓取与推送弹药功能。

图1 弹药传输机械臂三维模型 Fig.1 3D model of the ammunition transfer manipulator

图2 弹药传输机械臂的结构原理 Fig.2 Structural model of the ammunition transfer manipulator
简化弹药传输机械臂,即①将弹药传输机械臂本体简化为升降加翻转部分。②将链条简化为集中质量加无惯量线性弹簧,见图3。其中XOY为笛卡尔坐标系;C1,C2,C3分别为链条、升降与翻转部分质心;L为C2与C3之距离;O2为翻转部分转轴中心,与升降部分质心重合;yl,y1,θ2分别为链条、升降部分与翻转部分位移(角位移);k1为弹簧刚度系数。③将翻转部分与驱动电机间减速器的转动惯量等效到电机输出轴上,电机输出轴与翻转部分由无惯量线性扭簧连接,见图4。其中k2为扭簧刚度系数;θd为电机输出轴转角。

图3 弹药传输机械臂与链条简化模型 Fig.3 Simplified model of the ammunition transfer manipulator with flexible chain

图4 柔性关节简化模型 Fig.4 Simplified model of the flexible-joint
基于以上简化模型,用Lagrange法建立系统动力学方程为
(1)

式中:ml,m1,m2为链条、升降与翻转部分质量;J2,I为翻转部分及等效到电机转轴上的转动惯量;g为重力加速度。
1.2奇异摄动模型
链条、翻转部分转铰柔性会引起系统弹性振动。刚柔位移误差不断累积会严重影响系统控制精度。因此,系统控制器设计不仅考虑弹药传输机械臂本体姿态位置控制,且须考虑系统柔性振动的主动抑制。本文采用奇异摄动法,将系统分解为快、慢两时间尺度子系统,针对各子系统分别设计控制器,再将两控制器相加获得系统混合控制器。
据式(1)建立系统的奇异摄动模型。引入柔性力变量为
z=K(q2-q)
(2)
定义z为系统的快时变变量,q为慢时变变量。引入新刚度矩阵为
K1=ε2K
(3)
式中:ε为正极小量。
将式(2)、(3)代入式(1),得系统奇异摄动模型为
(4)
分别求解奇异摄动模型的慢、快时变子系统。
1.2.1慢时变子系统
设ε=0,由式(4)第二式得
(5)
将式(5)代入式(4)第一式,得慢时变子系统动力学方程为
(6)
式中:τs为慢时变子系统广义控制力。
H(q)=D1(q)+D2
(7)
可见,慢时变子系统动力学方程与不考虑柔性时系统刚性动力学方程完全相同。
式动力学方程具有性质[18]为
性质1惯量矩阵H(q)为正定对称矩阵,且上下有界,即对任意向量λ,有
mλ2≤‖λTH(q)λ‖≤Mλ2

性质2惯量矩阵H(q)的偏微分大小有界,即
性质3存在常数τ0>0,使广义控制力向量满足‖τs‖≤τ0。
1.2.2快时变子系统
由式(4)第一式得
(8)
将式(8)代入式(4)第二式,得
(9)

(10)
将ε=0代入式(10),得
(12)
将式(11)代入式(12),得
(13)
式中:τf=τ-τs为快时变子系统广义控制量。
引入快变时间尺度σ=t/ε,式(13)可改写为
(14)

(15)
2控制器设计
2.1混合控制策略
由计算过程可知,系统控制输入由慢时变子系统控制量τs与快时变子系统控制量τf组成,即
(16)
其中,慢时变子系统控制器作用为实现弹药传输机械臂位置控制;快时变子系统控制器作用为实现系统柔性振动主动抑制。见图5。
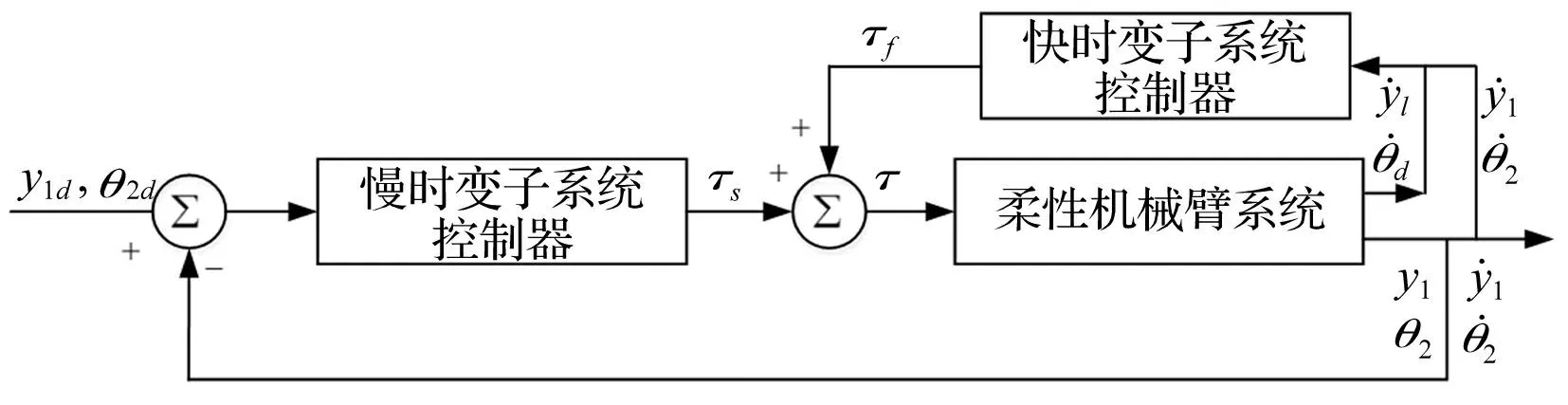
图5 弹药传输机械臂混合控制原理 Fig.5 Composite control of the ammunition transfer manipulator
分别设计快、慢时变子系统的控制器。选择快时变子系统控制器为
(17)
式中:Kf=K2/ε,K2为正定对角阵。可通过速度差值反馈不断调节保证系统稳定性。
2.2慢时变子系统控制器设计
2.2.1控制器设计
考虑系统惯量不确定即负载变化,视其与式(6)中重力项为系统所受不确定扰动,则弹药传输机械臂的刚性不确定动力学方程可写为
(18)
式中:S为不确定扰动,含重力项与惯量不确定项Δ。
S=-G(q)+Δ
(19)
设S大小有界,即存在S0>0,使‖S‖≤S0。选慢时变子系统控制器为
(20)
式中:
(21)
(22)
2.2.2稳定性分析
引入变量为
(23)
将式(21)、(23)代入式(22),化解得
16x4-ξ2x2-ηx-γ2=0
(24)
式中:x为变量;ξ,η,γ为方程系数,满足两条件:
条件1由H(q)的正定性,易得关系式
ξ2+γ2≥0
(25)
条件2据Cauchy不等式,得
(26)
即

(27)
定理1对满足条件、(27)的方程
f(x)=16x4-ξ2x2-ηx-γ2=0

据柯西不等式、式(21)可得不等式为
(28)
由式(22)、(28)得
(29)
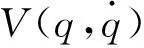
(30)
式中:
(31)
因H(q)可逆,则据式(18)有
(32)
将式(31)、(32)代入式(30),化解得
(33)

(34)
因
(35)
式(34)可化解为
(36)
分别化解式(36)右边三项。据式(21)、(22)得
(37)
由柯西不等式与性质2得

(38)
据式(29)与式性质1得
(39)
将不等式(39)代入式(38),得
(40)
由柯西不等式、性质1与‖S‖≤S0得
(41)
定义
(42)
将式(37)、 (40)~ 式(42代入式(36),得
(43)
证明:B恒大于零。由式(42)得
(44)
由式(28)可知
(45)
将式(45)代入式(44),得
(46)
由上式知,对任意非零系统状态,B总大于零。将式(44)的B移到不等号右边,得
(47)
(48)
定理 2选恰当的系统初始状态,使δ初始值大于零,即
δ(t0)>0
(49)

(50)
(51)
3数值计算
选系统仿真参数为:m1=10 kg,m2=40 kg,ml=2 kg,L=0.074 m,J=5 kgm,I=0.01 kgm,g=9.8 N/kg,k1=2×106N/m,k2=2×104Nm/rad。弹药传输机械臂本体姿态的初始值为
(52)
设弹药传输机械臂本体姿态目标值为
(53)
系统状态与终点状态间距离小于0.01时,认为已达到实际控制精度要求,结束计算,即
(54)
选慢时变子系统控制器参数为τ0=4 000,M=50.19;快时变子系统控制器参数为Kf=diag(200,2.6)。分别选开启、关闭快时变子系统控制器,在MATLAB中进行两组仿真实验进行对比,以凸显快时变子系统控制器对系统柔性的抑制作用。
为验证慢时变子系统控制器对系统负载变化的鲁棒性,增加一组仿真实验,即在第二组仿真实验基础上,将系统翻转部分惯量参数增加10%,而控制参数保持不变。仿真结果见图6~图12。各图(a)为关闭快时变子系统控制器时,系统在其作用下位置与速度响应、跟踪误差与控制激励曲线。由图6(a)~图9(a)可见,升降部分与翻转部分运动曲线相对链条与电机输出轴运动曲线呈规律振荡特征,振荡幅值随时间历程不断增加,呈现继续发散趋势。显然,仿真结束条件(52)永远无法得到满足,因此在t=0.4 s时设置主动中断。图10(a)、11(a)、12(a)分别为慢时变子系统控制器的控制输入与系统Lyapunov函数时间历程曲线。显然,亦呈逐渐振荡发散趋势。各图(b)、(c)为快、慢时变子系统控制器共同作用下系统位置与速度响应、跟踪误差与控制激励曲线,图(b)对应标称系统,图(c)对应惯量参数不确定系统。由图6(b)、(c)~图9(b)、(c)可见,升降部分与翻转部分的振荡迅速得到抑制,几乎完全衰减。由图10(b)、(c)与图11(b)、(c)可知,系统的控制输入曲线仅在仿真初始阶段内出现短期振荡,而系统的Lyapunov函数曲线始终单调递减。由各图(b)、(c)可见,标称系统与惯量参数不确定性的响应曲线基本相似,两者主要差别体现于总仿真时长,分别用时0.364 s、0.389 s。

图6 升降部分位移 Fig.6 Position of the lifting part

图7 翻转部分角位移 Fig.7 Angle of the revolving part

图8 升降部分速度 Fig.8 Velocity of the lifting part

图9 翻转部分角速度 Fig.9 Angular velocity of the revolving part
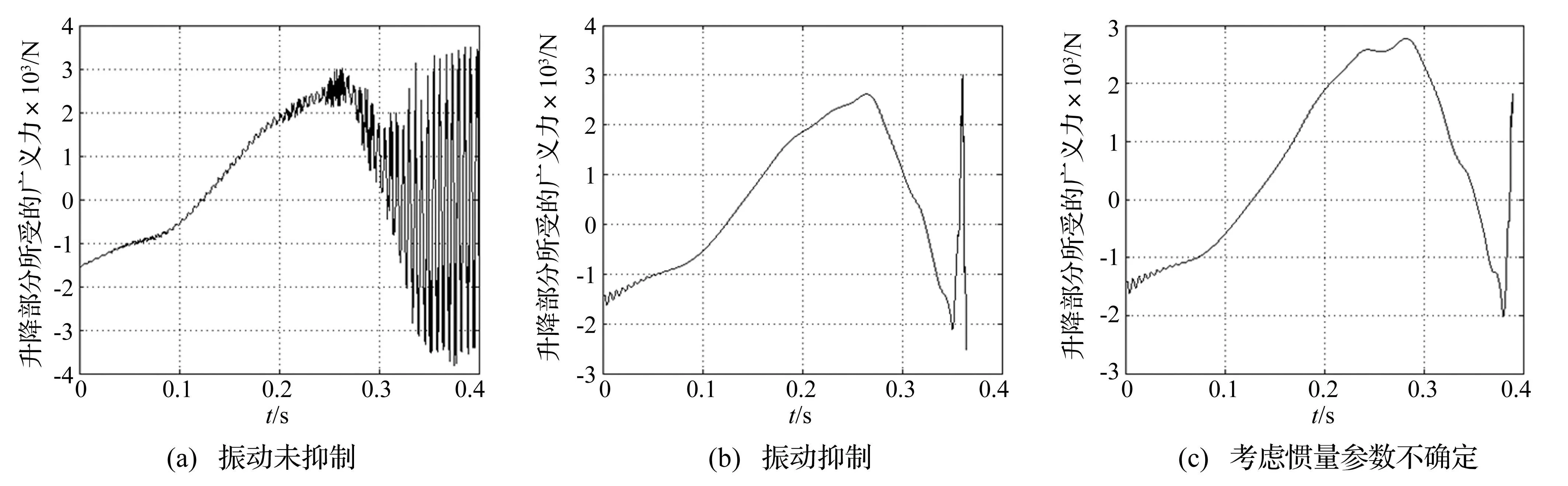
图10 升降部分控制力 Fig.10 Control forces of the lifting part

图11 翻转部分控制力矩 Fig.11 Control tor que of the revolving part

图12 Lyapunov函数值 Fig.12 Lyapunov Function
4结论
(1)针对现有坦克自动装弹机无法实现任意角度装填问题,提出两自由度弹药传输机械臂。该机械臂安装于车体内部,在弹药仓与炮尾之间,兼有任意角度协调、抓取及推送弹药功能。
(2)链条与翻转部分的减速装置同属驱动装置与被驱动部件之间的传动部件,二者柔性因素均可假设为线性无惯量弹簧。可用第二类Lagrange方法建立系统的刚柔耦合动力学方程。
(3)引入不同时间尺度,采用奇异摄动法将动力学模型分解为快、慢时变两个子系统,设计出以驱动与被驱动部件速度差值为反馈的控制器及基于隐式Lyapunov函数的位置控制器。
(4)控制器表现为增益时变的PD反馈控制。控制器增益作为系统状态变量的可微函数,随系统状态变量逐渐趋于零,该增益逐渐趋于无穷大,控制力始终满足给定约束。
(5)设计的混合控制器能克服负载变化及柔性振动影响,实现弹药传输机械臂点到点位置控制及柔性振动抑制,具有较强的鲁棒性。
参考文献
[1]侯保林,樵军谋,刘琮敏. 火炮自动装填[M]. 北京:兵器工业出版社, 2010: 36-38.
[2]Sullivan M B. Apparatus for autoloading tank cannons[P]. U.S.:5261310, 1993-10-16.
[3]Spong M W. Modeling and control of elastic joint robots[J]. Journal of Dynamics Systems, Measurement, and Control, 1987, 109(4): 310-319.
[4]郭闯强. 空间大型机械臂关节控制系统及轨迹规划研究[D]. 哈尔滨: 哈尔滨工业大学, 2012:16-17.
[5]Shi J X, Albu-Schaeffer A, Hirzinger G. Key issues in dynamic control of lightweight robots for space and terrestrial applications[J]. IEEE International Conference on Robotics and Automation,1998,1:490-497.
[6]郭闯强,倪风雷,孙敬颋,等. 具有力矩传感器的柔性关节的振动抑制[J]. 机器人, 2011, 33(4): 449-454.
GUO Chuang-qiang, NI Feng-lei, SUN Jing-ting, et al. Vibration suppression for the flexible joint with torque sensor[J]. Robot, 2011, 33(4): 449-454.
[7]Ulrich S, Sasiadek J Z. Trajectory tracking control of flexible joint space manipulators[J]. Canadian Aeronautics and Space Journal, 2012, 58(1): 47-59.
[8]彭济根,倪元华,乔红. 柔性关节操作手的神经网络控制[J]. 自动化学报, 2007, 33(2):175-180.
PENG Ji-gen, NI Yuan-hua, QIAO Hong. Neural network control of flexible-joint robot manipulatrs[J]. Acta Automatic Sinica, 2007, 33(2): 175-180.
[9]梁捷, 陈力. 关节柔性的漂浮基空间机器人基于奇异摄动法的轨迹跟踪非奇异模糊Terminal滑模控制及柔性振动抑制[J]. 振动与冲击, 2013, 32(23): 7-12.
LIANG Jie, CHEN Li. Nonsingular fuzzy terminal sliding mode control and elastic vibration suppression of a free-floating space robot with flexible joints based on trajectory tracking of the singular perturbation method[J]. Journal of Vibration and Shock, 2013, 32(23): 7-12.
[10]Shao Zhi-yu, Zhang Xiao-dong. Intelligent control of flexible-joint manipulator based on singular perturbation[A]. In: 2010 IEEE International Conference on Automation and Logistics[C]. Hong Kong and Macau, China, 2010:243-248.
[11]赵志刚. 空间站机械臂转位控制与振动抑制研究[D]. 哈尔滨:哈尔滨工业大学, 2013:104-106.
[12]陈健康,葛连正,李瑞峰. 考虑摩擦特性的机器人柔性关节鲁棒控制器设计[J]. 吉林大学学报:工学版, 2014.
CHEN Jian-kang, GE Lian-zheng, LI Rui-feng. Design of robust controller for robot flexible joint with friction characteristic[J]. Journal of Jilin University:Engineering and Technology Edition, 2014.
[13]党进,倪风雷,刘业超,等. 基于新型补偿控制策略的柔性关节控制器设计[J]. 机器人, 2011,33(1): 150-155.
DANG Jin, NI Feng-lei, LIU Ye-chao, et al. Design for flexible joint controller based on a new compensation control strategy[J]. Robot, 2011,33(1): 150-155.
[14]党进,倪风雷,刘业超,等.一种前馈补偿和模糊滑模相结合的柔性机械臂控制[J]. 西安交通大学学报,2011,5(3):75-80.
DANG Jin, NI Feng-lei, LIU Ye-chao, et al.Control strategy for flexible manipulator base on feedforward compensation and fuzzy-sliding mode control[J]. Journal of Xi’an Jiaotong Unversity, 2011, 5(3): 75-80.
[15]Chaoui H, Gueaieb W, Biglarbegian M, et al. Computationally efficient adaptive type-2 fuzzy control of flexible-joint manipulators[J]. Robotic, 2013, 2: 66-91.
[16]Anan’yevskii I M. Continuous feedback control of perturbed mechanical systems[J]. Journal of Applied Mathematics and Mechanics, 2003, 67(2): 293-305.
[17]Chernousko F L, Ananievski I M, Reshmin S A. Control of nonlinear dynamical systems:methods and applications [M]. Berlin:Springer, 2008:213-229.
[18]featherstone R, Orin D E. “Dynamics” in, handbook of robotics[M]. Berlin:Springer-Verlag Berlin Herdelberg, 2008:44.

第一作者谭仪忠男,博士生,1986年10月生
通信作者刘元雪男,教授,博士生导师,1969年生

